Optimal Control of the Future via Prospective Foraging (2511.08717v1)

Abstract: Optimal control of the future is the next frontier for AI. Current approaches to this problem are typically rooted in either reinforcement learning or online learning. While powerful, these frameworks for learning are mathematically distinct from Probably Approximately Correct (PAC) learning, which has been the workhorse for the recent technological achievements in AI. We therefore build on the prior work of prospective learning, an extension of PAC learning (without control) in non-stationary environments (De Silva et al., 2023; Silva et al., 2024; Bai et al., 2026). Here, we further extend the PAC learning framework to address learning and control in non-stationary environments. Using this framework, called ''Prospective Control'', we prove that under certain fairly general assumptions, empirical risk minimization (ERM) asymptotically achieves the Bayes optimal policy. We then consider a specific instance of prospective control, foraging, which is a canonical task for any mobile agent, be it natural or artificial. We illustrate that existing reinforcement learning algorithms fail to learn in these non-stationary environments, and even with modifications, they are orders of magnitude less efficient than our prospective foraging agents. Code is available at: https://github.com/neurodata/ProspectiveLearningwithControl.

• The paper presents a unified PL+C framework that integrates prediction and control to achieve Bayes optimal policies in non-stationary environments.
• It introduces the Prospective Foraging algorithm employing dual learners to estimate instantaneous and cumulative losses, achieving optimal regret with high data efficiency.
• Experimental results confirm that ProForg significantly outperforms traditional RL methods in learning speed and sample efficiency in dynamic settings.

Optimal Control of the Future via Prospective Foraging

Introduction and Motivation

The paper presents a unified framework for learning and control in non-stationary environments, extending the foundations of Probably Approximately Correct (PAC) learning and incorporating prospective learning. Unlike classical PAC frameworks that assume i.i.d. data, the proposed Prospective Learning with Control (PL+C) paradigm models environments where an agent's actions influence future data distributions—a critical aspect for any real-world agent or autonomous system. The authors concretely instantiate PL+C in the form of Prospective Foraging (ProForg), a canonical task where an agent must navigate and accumulate resources in a dynamic setting.

Formal Framework: Prospective Learning with Control (PL+C)

PL+C advances PAC and prospective learning by considering stochastic decision processes. The formalism explicitly distinguishes between prediction (where the loss is based on observed truth) and control (where loss is a negative reward, often unobserved for counterfactual actions). Key elements include:

• State Space: $x_t \in \mathcal{X}$ (agent's position), $t \in \mathcal{T}$ (time index)
• Rewards: $y_t \in \mathcal{Y}$, such that $\mathcal{Y} = \mathbb{R}_+^{|\mathcal{X}|}$ for all possible locations.
• Hypothesis: $h: \mathcal{X} \times \mathcal{T} \to \mathcal{X}$, possibly extended to $$h: \mathcal{X} \times \mathcal{T} \to \mathcal{X} \times \mathcal{Y}$$ for reward inference.
• Instantaneous Loss: $-\mathbb{E}_{z_{>t}}[y_{s+1}(x_{s+1})]$; cumulative loss is temporally weighted.
• Goal: Find learners $\mathcal{L}$ such that empirical risk minimization (ERM) converges to Bayes optimal policy with respect to cumulative discounted reward.

The framework overcomes limitations of MDP-based RL and regret-minimization in online learning, as neither fully relaxes the i.i.d. assumption nor models decision-dependent futures.

Theoretical Results

The authors provide rigorous theoretical guarantees for PL+C:

• Consistency: Under mild assumptions—existence of growing hypothesis classes, consistency, and uniform concentration—a sequence of hypotheses exists whose prospective loss converges to Bayes optimal.
• Concentration Bounds: The discrepancy between partial cumulative loss and infinite-horizon prospective loss is bounded and vanishes asymptotically.
• Extension: The proofs leverage techniques such as Borel-Cantelli and Markov's inequality, ensuring the stability and optimality of policy learning in non-stationary, decision-dependent environments.

Algorithmic Instantiation: Prospective Foraging (ProForg)

The central algorithm, ProForg, operationalizes PL+C via:

1. Warm Start: Random exploration for $N$ steps to gather initial data and facilitate subsequent model fitting.
2. Dual Learner Approach:
   • Instantaneous Loss Regressor ($\hat{g}^i$): Maps current state to immediate expected reward.
   • Cumulative Loss Regressor ($\hat{g}^p$): Maps state to the discounted sum of future rewards (terminal cost).
3. Online Rollouts and Lookahead: For each decision, the algorithm evaluates all feasible trajectories within a finite horizon via exhaustive search (or MCTS if computational limits preclude full search), optimizing for maximal cumulative prospective return.
4. Counterfactual Reward Estimation: Unobserved rewards (for actions not taken) are predicted using the learned models, enabling accurate evaluation of hypothetical futures.

Algorithmic details are clearly codified and can be mapped onto any supervised learning backbone (random forest, neural network, etc.), with temporal and positional features embedded for non-stationarity handling.

Experimental Findings

Empirical validation is conducted in a 1-D prospective foraging environment:

• Efficiency and Optimality: ProForg rapidly achieves Bayes optimal regret, outperforming both classical RL algorithms (Fitted Q-Iteration, Soft Actor-Critic) and their time-aware variants by orders of magnitude.
• Necessity of Non-stationary Modeling: Time-agnostic variants of RL fail to converge to optimal regret, consistently underperforming regardless of sample size.
• Data Efficiency: Online ProForg learns with up to 4x fewer data points compared to offline random exploration strategies.

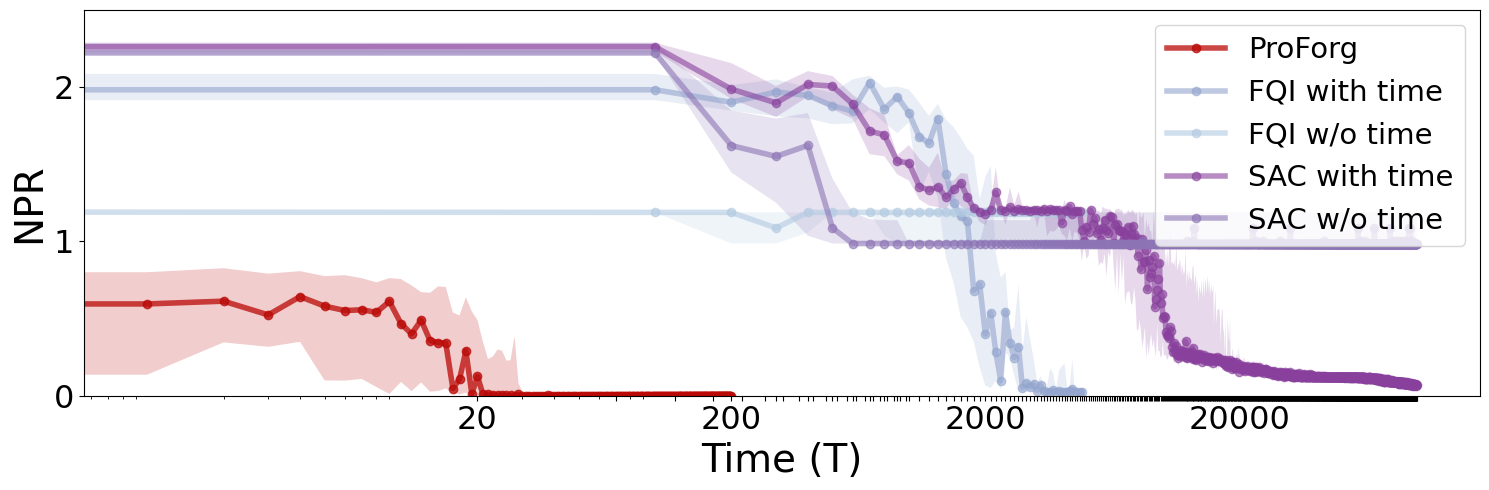
  Figure 1: ProForg efficiently achieves Bayes optimal regret, substantially outpacing RL baselines with and without time-awareness.

  

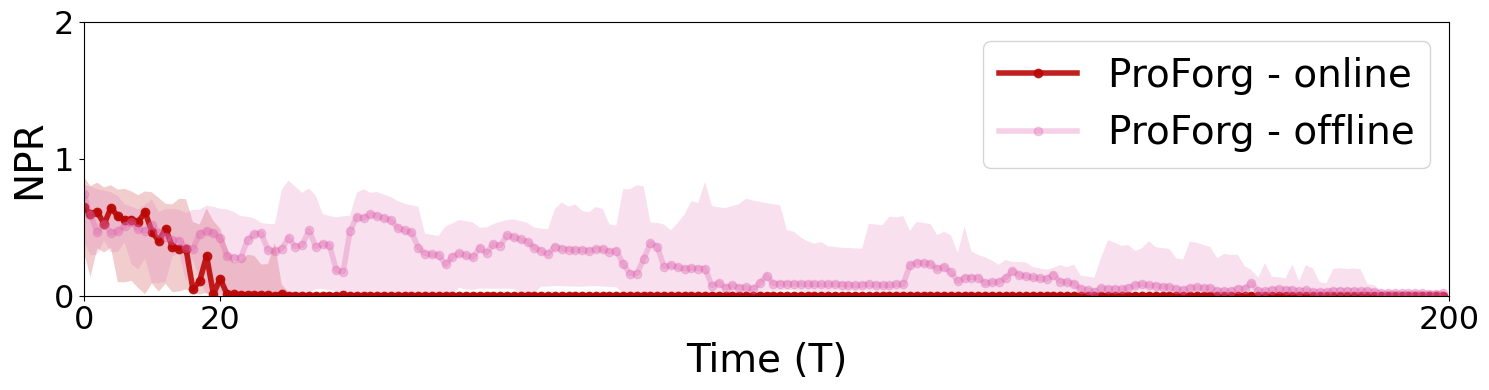
  Figure 2: Online ProForg is markedly more sample-efficient than offline, converging to optimality with dramatically less data.

• Dual-Learner Advantage: Ablation studies demonstrate that either instantaneous or cumulative loss modeling alone is insufficient; only their combination yields accelerated convergence and optimal policy learning.

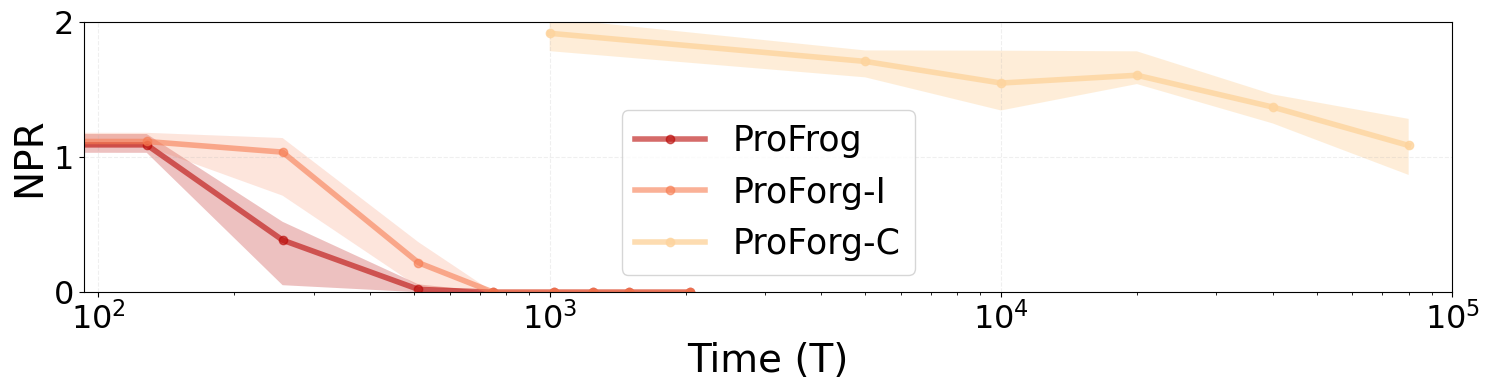
  Figure 3: Removing either instantaneous or cumulative component decreases learning efficiency and asymptotic performance relative to ProForg.

• Choice of Regressor: While random forests yield rapid convergence, deep neural networks also attain optimality but with decreased data efficiency—highlighting the trade-off between model expressivity and inductive bias.

Implications and Future Directions

Theoretical Impact

PL+C formalizes a unified optimal control and learning theory for non-stationary, decision-dependent environments—a critical advance over stationary PAC, RL, and OL frameworks. The connection to causal inference is notable: PL+C manages structural dependencies between agent interventions and future data distributions, akin to potential outcomes in causal modeling.

Practical Applications

• Robotics and Autonomous Systems: ProForg's dual-learner strategy and prospective planning can be readily integrated into agents operating in dynamic, resource-constrained domains—e.g., adaptive exploration robots, supply chain logistics.
• Generalization Potential: The methodology generalizes beyond discrete foraging into continuous state/action/time spaces and higher-dimensional settings.
• Integration with Deep Learning: As demonstrated, backbones such as MLPs can be leveraged, though at cost to sample efficiency.

Limitations and Future Work

• Scalability: The combinatorial trajectory evaluation scales exponentially with horizon and action space. Incorporation of more advanced planning (e.g., MCTS, policy distillation) is suggested for complex environments.
• Partial Observability and Causality: Extending PL+C to partially observed, stochastic causal graphs or POMDPs would further enhance applicability.
• Real-world Deployment: Application to domains such as dynamic resource allocation, complex real-world robotic foraging, or continuous control is an open avenue.

Conclusion

The PL+C framework and the ProForg algorithm represent robust methodologies for learning and optimal control in environments where actions shape future data distributions. Unlike classical RL, PL+C leverages empirical risk minimization to achieve optimal policies under non-stationarity, theoretically supported and empirically validated. The implications for both theory and real-world systems are substantial, with future research anticipated in scaling, generalization, and the integration of richer model architectures.