Realization of an all-optical effective negative-mass oscillator for coherent quantum noise cancellation (2511.08056v1)

Abstract: We report the realization of an all-optical, tabletop effective-negative-mass oscillator (ENMO) scheme capable of canceling quantum noise when cascaded with an opto-mechanical sensor susceptible to (quantum) radiation pressure noise. Our coherent quantum noise cancellation (CQNC) scheme offers a broadband cancellation capability with a tunable, wavelength-flexible, and compact system. This is achieved through the implementation of an optical equivalent of an opto-mechanical interaction, facilitated by a down-conversion and a beam-splitting process. The intricate nature of the system and its multiple interacting components made characterizing the interdependent parameters with conventional methods ineffective, leading to the development of an in-situ characterization scheme. The obtained parameters meet the targets for CQNC set in previous studies. With our current realization, we project a broadband quantum noise reduction of 3.6 dB, corresponding to a 77% reduction in quantum back-action noise at the optimal frequency of maximum reduction, indicating the readiness of the ENMO for application. We discuss the prospects for new applications in quantum information and communication using the same platform.

• The paper presents a novel all-optical engineered negative-mass oscillator that achieves coherent quantum noise cancellation with 3.6 dB noise reduction.
• It details an optical cavity design using a type II PPKTP crystal and tunable photon-photon interactions to match and invert system susceptibilities.
• Experimental results indicate scalability to nearly 11.9 dB cancellation, highlighting potential applications in precision quantum sensors.

All-Optical Effective Negative-Mass Oscillator for Coherent Quantum Noise Cancellation

Introduction and Motivation

Quantum noise, particularly quantum back-action (QBA), constitutes a fundamental limitation for precision optomechanical sensors, including gravitational wave detectors, atomic sensors, and platforms for quantum information processing. Coherent quantum noise cancellation (CQNC) proposes the integration of an engineered negative-mass oscillator (ENMO) to destructively interfere with and thus cancel QBA components introduced by optomechanical systems (OMS). This paper demonstrates, for the first time, a fully optical ENMO both with tunable parameters and compact tabletop implementation, overcoming key limitations of previous atom-based and opto-mechanical approaches.

The core conceptual breakthrough is the all-optical engineering of a negative-mass response using photon-photon interactions, as opposed to atomic ensembles or mechanical oscillators. By matching system susceptibilities and interaction Hamiltonians, the ENMO generates an inversely squeezed quantum state, enabling near-perfect QBA cancellation when cascaded with an OMS.

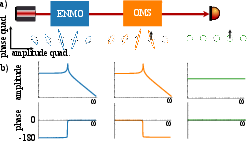
Figure 1: Cascaded CQNC system illustrating tailored inverse squeezing for broadband QBA cancellation; quantum noise ellipses reveal signal recovery.

Theoretical Framework

CQNC relies on generating two independently tunable oscillator systems—one physical (OMS), one effective (ENMO)—with matched, but phase-opposed susceptibilities. QBA arises from the ponderomotive effect: light's amplitude (intensity) fluctuations impart radiation pressure to a mechanical element, which, in turn, imprints phase noise back onto the outgoing light field. This entangles amplitude and phase quadratures (ponderomotive squeezing), obscuring weak signals.

To counteract this, the ENMO must implement an interaction Hamiltonian

$$H_{ENMO} = \frac{g_{ENMO}}{2} \left[(a_m c_m + a_m^\dagger c_m^\dagger) + (a_m c_m^\dagger + a_m^\dagger c_m)\right]$$

analogous to radiation pressure in the OMS, but with sign-reversal and fully optical modes. The ENMO then outputs an inversely squeezed state, and, upon cascading with the OMS, QBA is canceled—restoring vacuum noise levels in the measurement quadrature.

The required condition, $\chi_m = -\chi_a$, mandates that the mechanical and effective negative-mass oscillator susceptibilities are equal in magnitude but opposite in phase, achieving destructive interference in QBA channels. This is realized by matching system linewidths and detunings—implementable through optical cavity engineering.

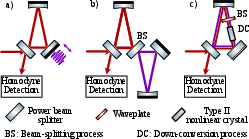
Figure 2: a) Standard optomechanical cavity; b) subsystem mapping to photon-photon interaction; c) polarization-encoded cavity with type II PPKTP crystal for practical ENMO realization.

Experimental Realization

Hardware Architecture

Implementation of the ENMO employs a birefringence-based, polarization-split optical cavity containing a type II PPKTP crystal:

• Orthogonal polarizations (p-pol for meter cavity, s-pol for ancilla cavity) act as independent oscillators.
• A waveplate introduces tunable beam-splitting between polarization modes.
• Parametric down-conversion induces two-mode squeezing between these modes, serving as the analogue to optomechanical coupling.
• The cavity employs highly reflective mirrors, with differential mirror reflectivities for the two polarizations, enabling independent linewidth control and minimizing loss.

Mechanical stability, susceptibility detuning, and tunability are achieved via temperature adjustment of the birefringent crystal and motorized waveplate stages. Homodyne detection with a p-pol local oscillator enables accurate quadrature measurement.

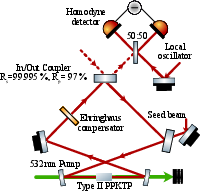
Figure 3: Optical realization of the ENMO as a polarization-coupled cavity with a type II PPKTP crystal, showing the coupling and squeezed state readout.

Measurement and Characterization

Due to the high degree of parameter interdependency, standard characterization techniques are insufficient. The authors introduce an in situ optimization method, fitting frequency-resolved homodyne variance traces across tunable cavity detunings. Key experimental capabilities demonstrated:

• Linewidths ($\kappa_c$, $\kappa_a$) matched to target OMS parameters (Si$_3$N$_4$ membrane resonators).
• Independently tunable squeezing ($g_{DC}$, down-conversion) and beam-splitting ($g_{BS}$), with achieved equality to within 5 kHz.
• Full tomographic reconstruction of output states reveals frequency-dependent squeezing angles and magnitudes—tailored for QBA cancellation.

  Figure 4: Frequency-resolved measurement of output squeeze variance for different ancilla detunings; b) quadrature tomography shows the engineered frequency-dependent squeezing.

Performance Analysis and Projected Enhancements

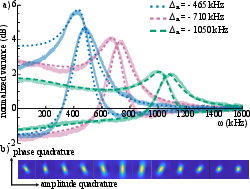
The current ENMO implementation, when combined with a simulated OMS, achieves up to 3.6 dB quantum noise cancellation, corresponding to 77% QBA noise reduction at optimal frequencies. Losses, dominated by AR coatings of intra-cavity elements, constitute the primary constraint on further enhancement.

Simulated projections for future setups (reduced ancilla linewidth, superior coatings, longer cavity) indicate feasibility for 11.9 dB (81% QBA reduction), approaching ultimate CQNC limits for all-optical platforms. The broadband character, ease of parameter tuning (beam-splitting, squeezing, susceptibility via detuning and power), and integration independence from OMS architecture allow for rapid adaptation to various quantum sensors.

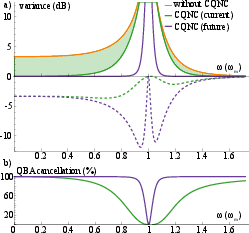
Figure 5: Simulated phase quadrature noise spectra illustrating broadband QBA suppression for current and projected future ENMO parameters; b) fractional QBA noise canceled versus frequency.

Control, Loss Budget, and Stability

Comprehensive control architecture is detailed, including:

• Pound-Drever-Hall locking for both cavity polarizations.
• Temperature and positional stabilization of the nonlinear crystal.
• Homodyne phase angle stabilization referenced to injected seed beams and lock-in detection.

The most critical resource, total detection efficiency (54% in current configuration), is allocated across propagation, homodyne, quantum, and escape efficiencies, with loss budget validation performed under single-mode squeezing.

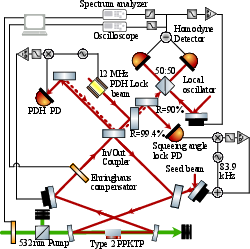
Figure 6: Schematic of control loops and auxiliary locking beams for ENMO operation.

Implications, Applications, and Future Directions

Key implications:

• CQNC with all-optical ENMO matches or exceeds the flexibility of atom-based schemes without wavelength restrictions or thermal decoherence.
• Platform is scalable to larger cavities for improved performance, while maintaining tabletop compatibility.
• The technology provides a photonic CQNC module suitable for integration with both resonant and non-resonant quantum sensors, including optomechanical force sensors, atomic interferometers, and gravitational wave calculators.
• The absence of mechanical elements in the ENMO eliminates thermal constraints, making the platform suitable for room-temperature operation and long photon storage times.

Potential applications:

• CQNC for quantum-limited inertial sensors and gravitational wave detectors.
• Optical quantum memory through selective retrieval and storage controlled by switching between down-conversion and beam-splitting interactions.
• Single-photon sources leveraging high-finesse, low-decoherence ancilla cavities.
• Time/frequency domain quantum optics experiments without the necessity for cryogenics.

Future advancements:

• Quantum state transfer between distinct optical and optomechanical systems.
• Rapid switching via EOM/AOM implementations; enables real-time control of CQNC protocol and storage/retrieval operations.
• Enhanced integration with quantum communication protocols including continuous-variable entanglement swapping.
• Exploration of new photonic quantum interfaces employing the ENMO design as a modular component.

Conclusion

This work establishes a tabletop, fully photonic ENMO system, which realizes the key theoretical promises of CQNC for broadband QBA mitigation. The experimental results match or exceed previous benchmarks, with clear pathways toward significant further performance enhancement through optical loss minimization and cavity design improvements. The versatility and wavelength flexibility, together with straightforward integration and in situ characterization methodologies, enable deployment both for fundamental quantum measurement applications and as a core technology for optical quantum information processing systems.