Can Training Dynamics of Scale-Invariant Neural Networks Be Explained by the Thermodynamics of an Ideal Gas? (2511.07308v1)

Abstract: Understanding the training dynamics of deep neural networks remains a major open problem, with physics-inspired approaches offering promising insights. Building on this perspective, we develop a thermodynamic framework to describe the stationary distributions of stochastic gradient descent (SGD) with weight decay for scale-invariant neural networks, a setting that both reflects practical architectures with normalization layers and permits theoretical analysis. We establish analogies between training hyperparameters (e.g., learning rate, weight decay) and thermodynamic variables such as temperature, pressure, and volume. Starting with a simplified isotropic noise model, we uncover a close correspondence between SGD dynamics and ideal gas behavior, validated through theory and simulation. Extending to training of neural networks, we show that key predictions of the framework, including the behavior of stationary entropy, align closely with experimental observations. This framework provides a principled foundation for interpreting training dynamics and may guide future work on hyperparameter tuning and the design of learning rate schedulers.

• The paper introduces a novel thermodynamic framework linking SGD hyperparameters to macroscopic quantities like temperature, pressure, and volume.
• It employs stochastic differential equations to explain weight distribution equilibria and validates predictions through numerical simulations across architectures.
• The work provides actionable insights for hyperparameter tuning via free-energy minimization and Maxwell relations, with implications for ensemble-based model averaging.

Thermodynamic Analysis of Scale-Invariant Neural Network Training

Introduction and Motivation

This paper establishes a rigorous connection between the training dynamics of scale-invariant neural networks (those with normalization layers such as BatchNorm and LayerNorm) and the thermodynamics of an ideal gas. It constructs a physical analogy, mapping SGD hyperparameters (learning rate, weight decay) to macroscopic thermodynamic quantities: temperature, pressure, and volume. By leveraging stochastic differential equation (SDE) analysis and focusing on scale invariance, the framework allows characterization of the stationary weight distributions induced by SGD as thermodynamic equilibrium states, enabling the introduction of free-energy minimization and Maxwell relations into hyperparameter analysis.

Theoretical Framework: From SDEs to Thermodynamic Potentials

The key abstraction involves decomposing weights into norm ($r = \|\mathbf{w}\|$) and direction ($\bar{w} = \mathbf{w}/\|\mathbf{w}\|$). Training dynamics are described by SDEs under three protocols: (1) constrained norm (projected SGD on a sphere), (2) fixed effective learning rate (ELR, controlling learning rate relative to norm), and (3) fixed learning rate (LR, usual SGD with weight decay). SDE analysis predicts convergence to stationary distributions for the direction and deterministic evolution of radius to a stationary value, $r^*$.

Using an isotropic noise model, the stationary distribution for the direction takes the Gibbs form:

$$\rho^*_{\bar{w}}(\bar{w}) \propto \exp\left( -\frac{L(\bar{w})}{T} \right)$$

where temperature $T$ is a monotonic function of learning rate and batch noise. The stationary radius $r^*$ satisfies a relation formally equivalent to the ideal gas law ($pV=RT$), with volume $V = r^2/2$, pressure $p$ corresponding to weight decay $\lambda$, and $R = (d-1)/2$ the effective dimension. The SDE induces minimization of thermodynamic potentials: Helmholtz energy $F = U-TS$ (projected sphere/fixed ELR) and Gibbs energy $G = U-TS+pV$ (fixed LR).

Figure 1: Results for the VMF isotropic noise model with fixed LR $\eta$ and WD $\lambda$. Theoretical predictions for stationary energy, entropy, and radius match numerical simulations; empirical minimization of Gibbs energy is consistent with theory.

Empirical Validation: Stationary Laws and Maxwell Relations

Experiments verify four critical predictions:

• Stationary radius scaling: $r^*$ scales as $\sqrt[4]{\eta/\lambda}$ for fixed LR and $\sqrt{\eta_\text{eff}/\lambda}$ for fixed ELR, mirroring the ideal gas relation;
• Thermodynamic potential minimization: Solutions minimize $F$ or $G$ among hyperparameter configurations, manifesting physical equilibrium selection;
• Maxwell relations: Partial derivatives of stationary entropy with respect to log-learning rate and log-weight decay satisfy physically motivated constraints, e.g. $$(\partial S/\partial \log \eta)_\lambda - (\partial S/\partial \log \lambda)_\eta = (d-1)/2$$;
• Adiabatic processes: Coordinated hyperparameter changes following $pV^\gamma = \mathrm{const}$ (with $\gamma=C_p/C_V$) conserve entropy, confirming reversibility in this macroscopic analogue.

  Figure 2: Results for ResNet-18 on CIFAR-10 with fixed LR $\eta$ and WD $\lambda$. Temperature $T$ and stationary radius $r^*$ accurately follow theoretical formulas. Entropy landscape confirms Maxwell relations.

Beyond Toy Models: Empirical Results for Neural Networks

The ideal gas analogy extends well to actual neural network training, albeit with caveats regarding gradient noise anisotropy. Empirical studies on ResNet-18 and ConvNet architectures trained on CIFAR-10/100 datasets show that:

• Gradient noise variance $\sigma^2$ is not strictly constant but exhibits systematic dependence on $\eta$ and $\lambda$ (primarily on their product), especially at large values;
• Stationary radius $r^*$, entropy, and temperature $T$ computed from measured $\sigma^2$ closely match theoretical expectations;
• Maxwell relations for entropy hold across architectures, with polynomial regression fits yielding coefficients consistent with analytic formulas (relative error $<10\%$ across the interior of the hyperparameter grid).

Additional results for other architectures and protocols (fixed ELR, training on spheres) further validate the theory.

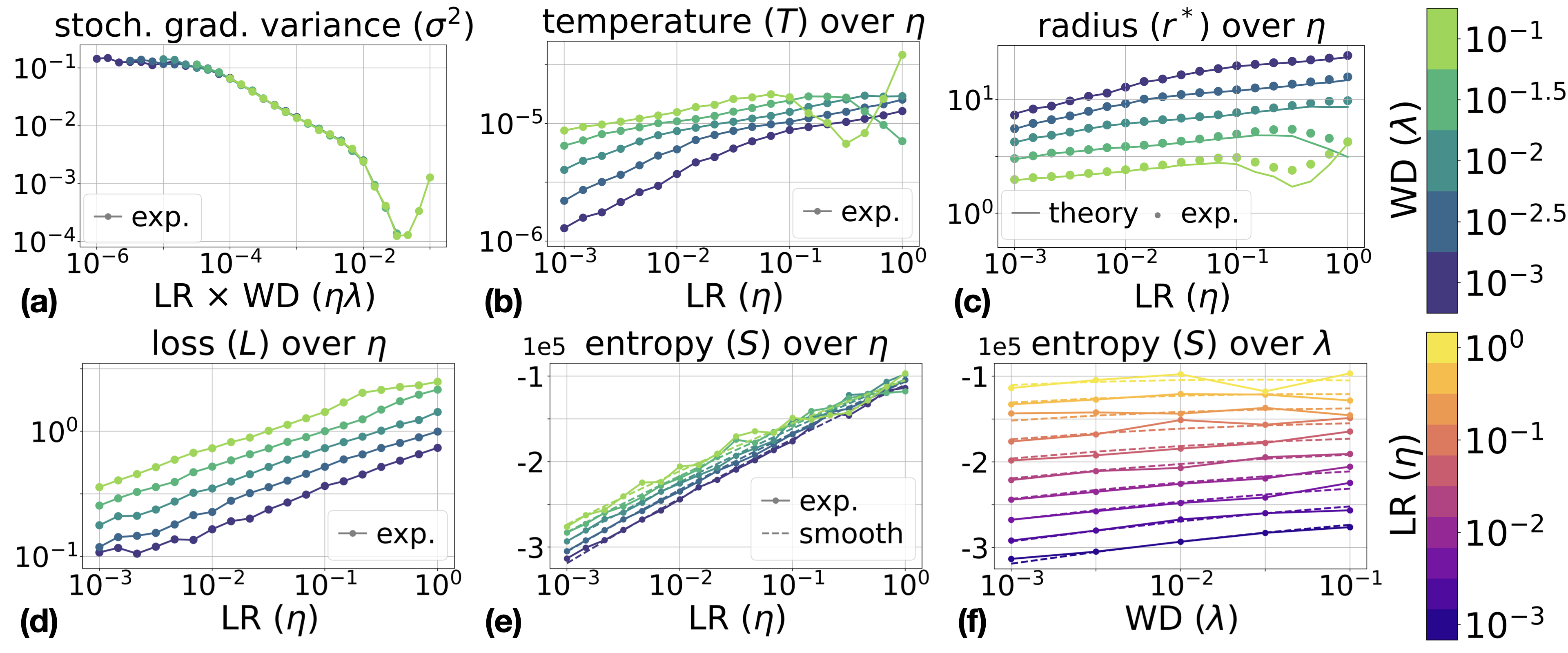
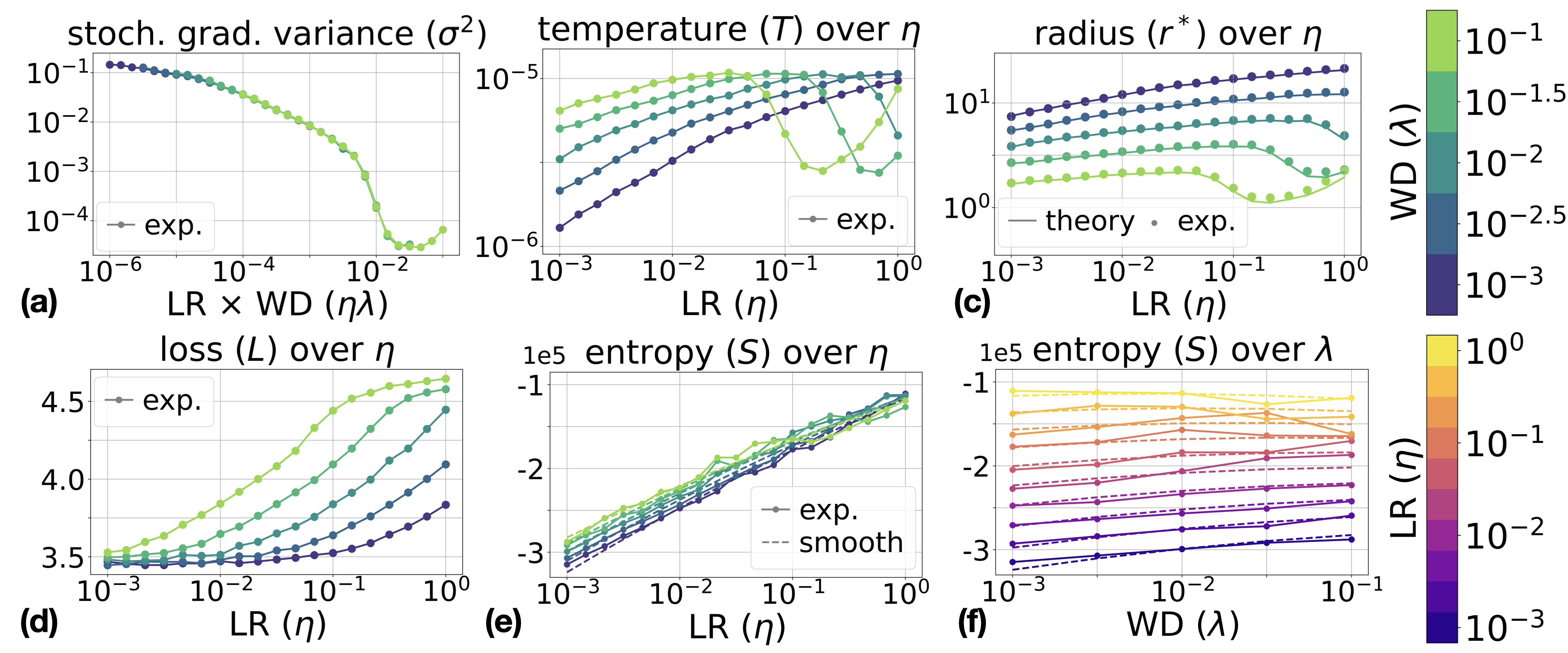
Figure 3: Results for ResNet-18 on CIFAR-10 and CIFAR-100 with fixed LR $\eta$ and WD $\lambda$. Empirical values for stationary radius and entropy derivatives (Maxwell relations) closely match theoretical predictions.

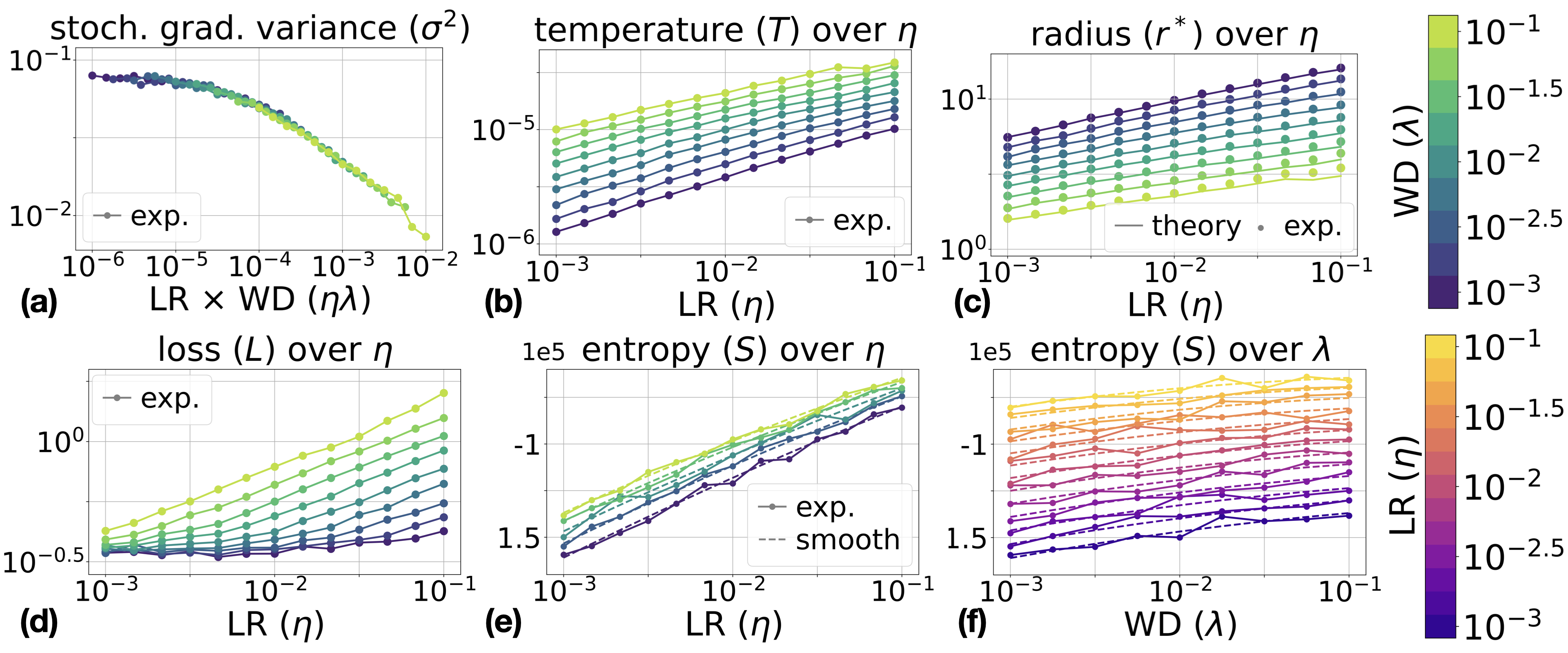
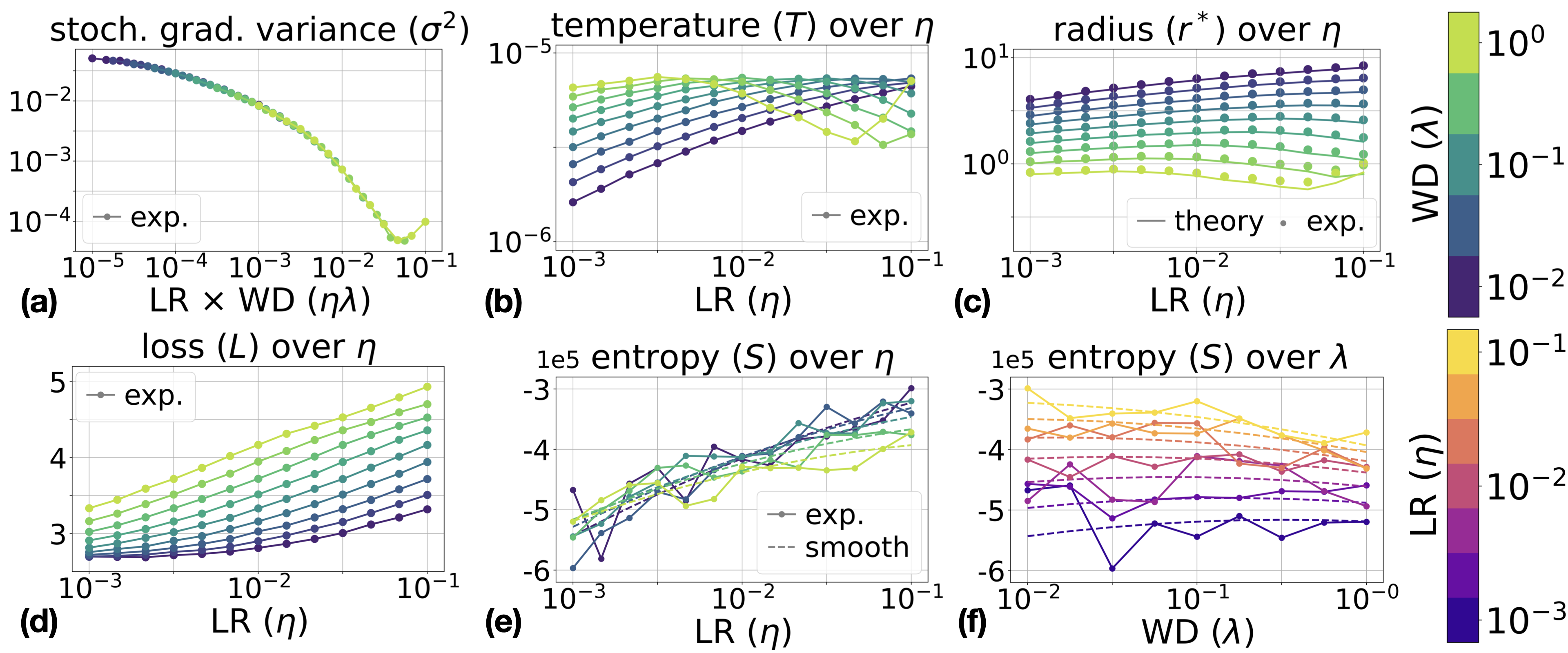
Figure 4: Results for ConvNet on CIFAR-10 and CIFAR-100 with fixed LR $\eta$ and WD $\lambda$. Observed values support the ideal gas analogy and entropy scaling laws.

Discretization Error and Overparameterized Regimes

For large learning rates or weight decays, discrepancies emerge between continuous SDE predictions and discrete-time SGD. These are traced to the non-negligible mean gradient norm acting as an effective centrifugal force, necessitating a correction term in the formula for $r^*$. Overparameterized networks in interpolation mode (capable of fitting training data exactly) also exhibit convergence rather than settling to a stationary distribution; as SGD noise vanishes, behavior degenerates to full-batch gradient descent, with stationary distributions collapsing to a point.

Figure 5: Comparison between discrete-time and SDE predictions of stationary radius and effective weight decay. The geometric correction term yields higher accuracy for large values of learning rate and weight decay.

Practical Implications and Extensions

• Hyperparameter tuning: The explicit mapping of optimizer variables to thermodynamic quantities enables principled design of learning rate/weight decay schedules, potentially guiding entropy evolution to prevent premature convergence and improve generalization.
• Weight averaging: Stationary entropy acts as a measure of model diversity. This is directly relevant to the efficacy of SWA/weight averaging for ensemble generalization, as high entropy favors better averaging despite individual loss values.
• Extensibility: Generalization to anisotropic noise and real gas equations is plausible via a compressibility factor. Extensions to non-scale-invariant networks and momentum-based optimizers (e.g., Adam) remain theoretically tractable but would involve more intricate SDEs and possibly nontrivial thermodynamic analogies.

Theoretical Impact and Future Directions

The work provides a rigorous physics-derived foundation for understanding optimization dynamics in deep learning. It elevates thermodynamic analogies beyond energy/entropy/temperature, introducing pressure and volume as directly measurable quantities tied to optimization control. Maxwell relations provide new analytic tools for quantifying the influence of hyperparameters on stationary solutions.

Open research directions include generalizing to more realistic noise models, incorporating momentum, and further integrating thermodynamic perspectives into standard training practices, hyperparameter search, and the analysis of generalization.

Conclusion

The presented framework successfully formalizes a direct mapping between SGD-driven training of scale-invariant neural networks and ideal gas thermodynamics. Empirical evidence strongly supports the theory across models and protocols, with key predictions manifesting in real neural network training. The approach offers both theoretical insight and practical mechanisms for optimizer design and analysis, representing a significant synthesis of statistical physics and machine learning methodology. Future work may further elaborate these connections for broader architectures and advanced optimization schemes.