Geometric Intermittency in Turbulence (2511.06439v1)

Abstract: Equal-time scaling exponents in fully developed turbulence typically exhibit non anomalous scaling in the inverse cascade of two-dimensional (2D) turbulence and anomalous scaling in three dimensions. We demonstrate that multiscaling is not confined to longitudinal, scalar velocity increments, but also emerges in increments associated with the magnitude and orientation of the velocity vector. This decomposition uncovers a multiscaling in the 2D inverse cascade, which remains obscured when using conventional structure functions. Our results highlight a decoupling between velocity amplitude and flow geometry, offering new insight into the statistical structure of turbulent cascades as well as showing how different classes of multiscaling emerge.

• The paper unveils a novel approach where velocity increments are decomposed into amplitude and geometric factors to expose hidden multiscaling in turbulence.
• It uses DNS data from the Johns Hopkins Turbulence Database to quantify distinct intermittent behaviors between classical and geometric measures.
• The findings suggest that incorporating geometric contributions can refine turbulence modeling and improve predictions in complex flow systems.

Geometric Intermittency in Turbulence

The paper "Geometric Intermittency in Turbulence" explores the phenomenon of intermittency in turbulent flows and introduces a novel perspective on the multiscaling observed in these systems. Traditional studies have focused primarily on longitudinal velocity increments and their associated structure functions in characterizing turbulence. However, this research uncovers significant multiscaling by examining increments in both the magnitude and orientation of the velocity vector, thereby providing deeper insights into the statistical structure of turbulent cascades.

Introduction to Turbulent Intermittency

Turbulent flows are characterized by erratic and irregular motion, leading to complex statistical behavior known as intermittency. Historically, Kolmogorov's 1941 theory provided a framework for understanding turbulence through longitudinal structure functions, $$S^{\rm L}_p(r) = \langle (\delta u^{\rm L}_r)^p \rangle$$, defined for velocity increments along the flow direction. These functions scale as $S^{\rm L}_p(r) \propto r^{\zeta^{\rm L}_p}$ within the inertial range, with scaling exponents $\zeta^{\rm L}_p$. Theory predicts linear scaling for $\zeta^{\rm L}_p$, yet experiments show deviations indicating multiscaling due to turbulence's intermittent nature.

Decomposing Velocity Increments

This paper extends the analysis of turbulence by decomposing velocity increments into contributions from velocity amplitudes and flow geometry. This decomposition reveals multiscaling in the inverse cascade regime of two-dimensional (2D) turbulence, typically considered non-anomalous, thereby highlighting new forms of intermittency.

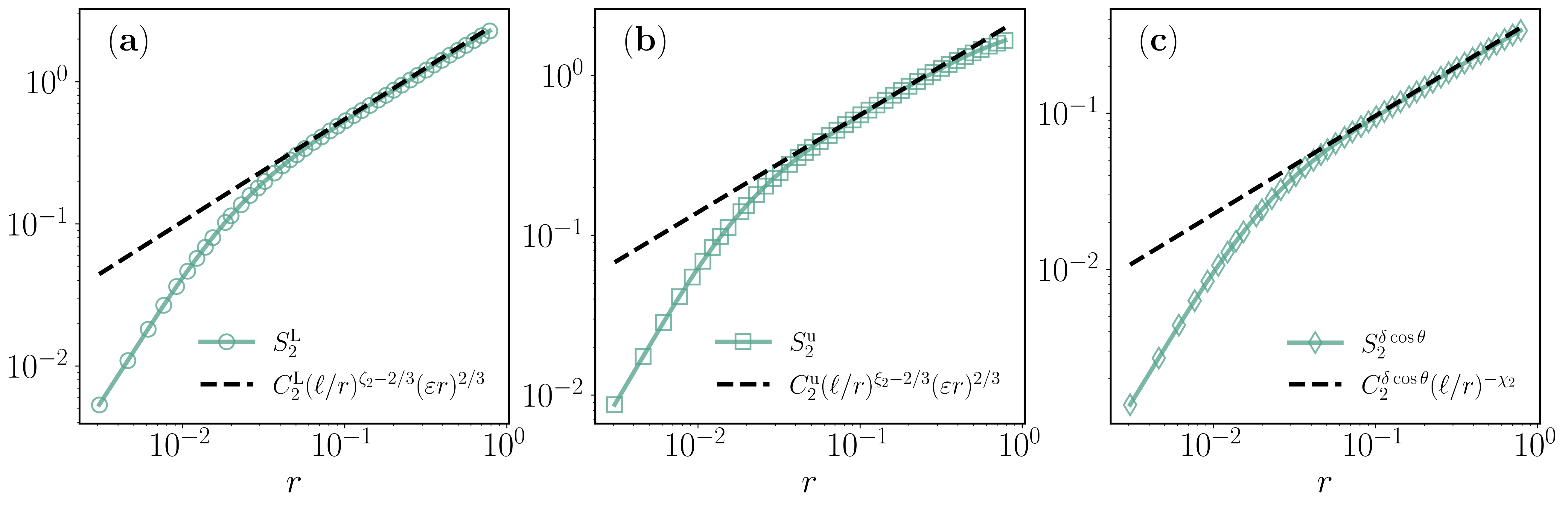
Figure 1: Loglog plots of the different second-order structure functions for increments of (a) the longitudinal velocity (b) velocity amplitudes and (c) the cosine-angles; revealing multiscaling through the inclusion of geometric factors.

The authors propose that intermittency in turbulence is not adequately described by velocity magnitude alone. By defining structure functions based on cosine-angle increments $$\delta \cos \theta_r = \cos \theta_{\rm B} - \cos \theta_{\rm A}$$, they demonstrate pronounced multiscaling characteristics often obscured in classical analyses.

Numerical Simulation Results

Utilizing data from Direct Numerical Simulations (DNS) accessed through the Johns Hopkins Turbulence Database (JHTD), the paper confirms these geometric contributions are significant. Analysis of the velocity amplitude $\delta u_r = u_{\rm B} - u_{\rm A}$ and angle increments reveals disparate behaviors in statistics and decay rates of correlations.

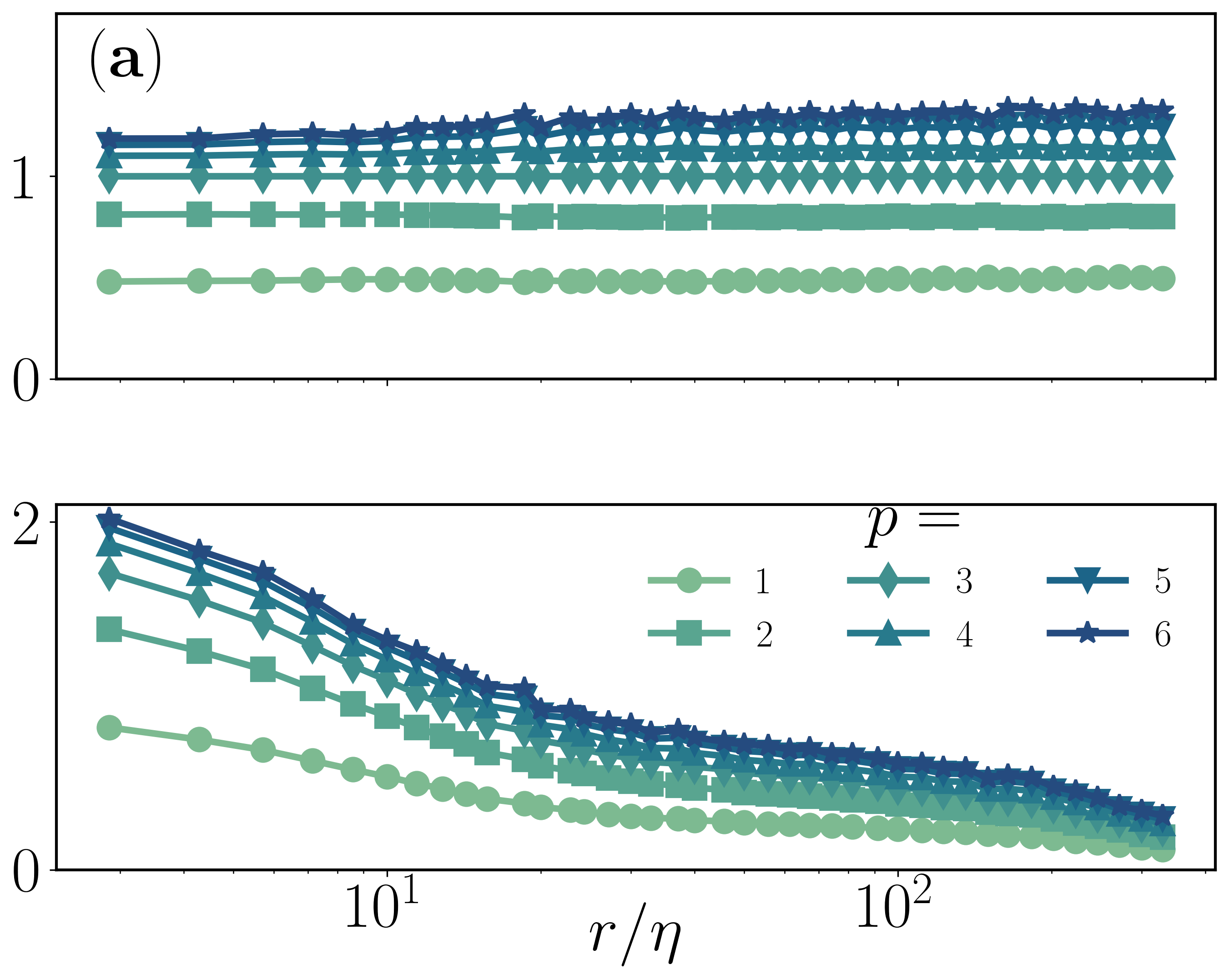
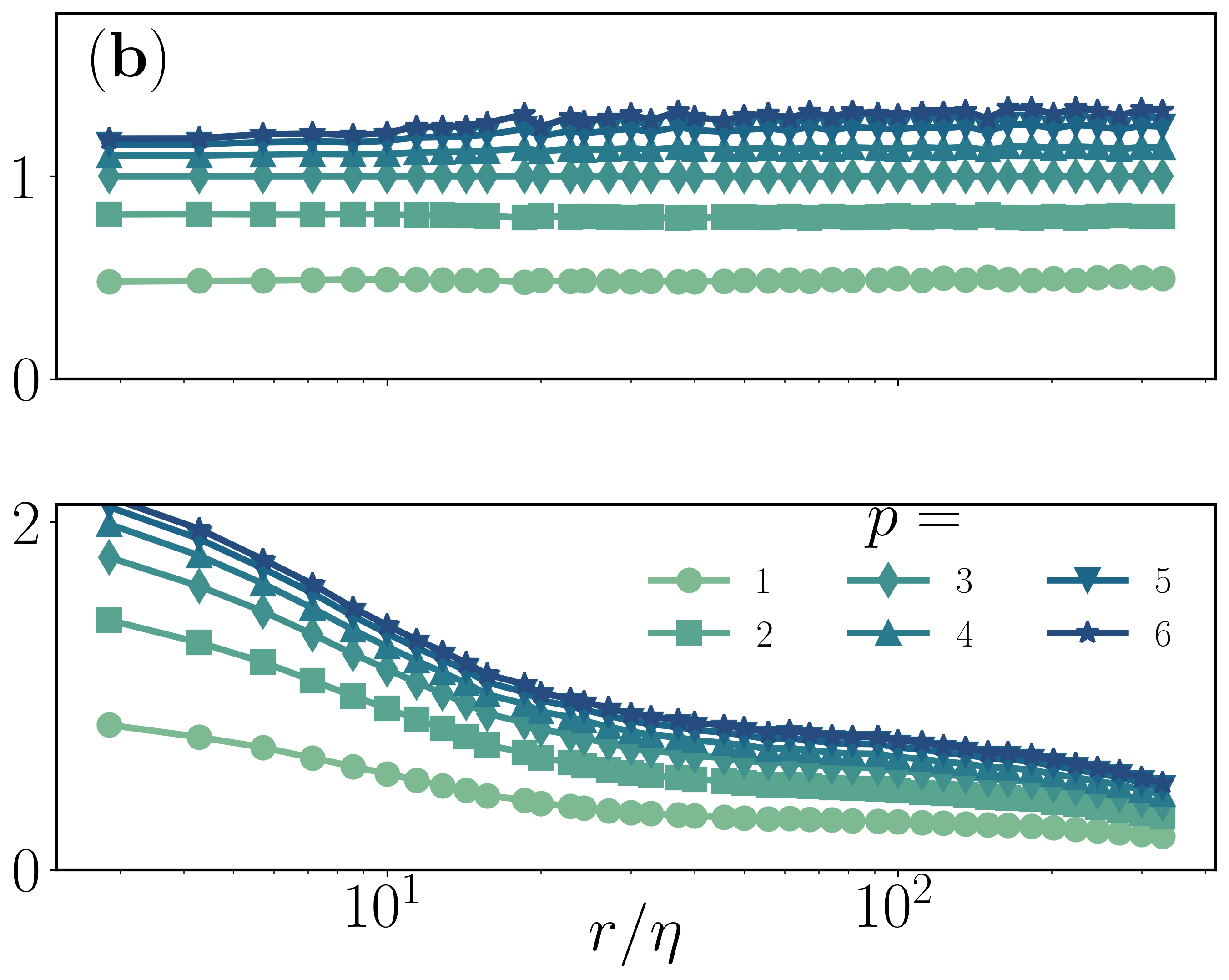
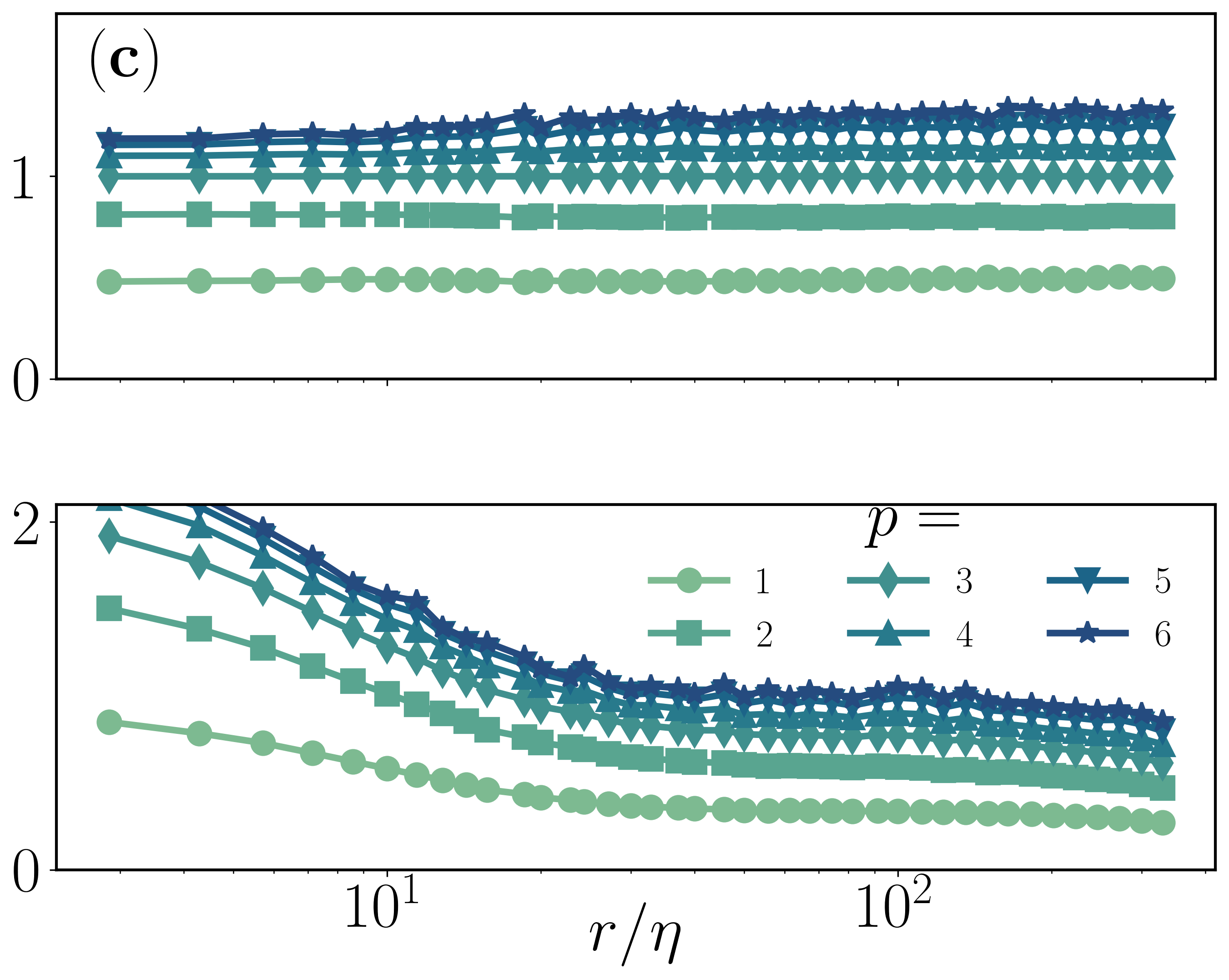
Figure 2: Plots of local slopes for structure functions increments $\delta\sin\theta_r$, showing the stark disparity between classical and geometric scaling.

The investigation shows that for both three-dimensional (3D) and 2D turbulence, these geometric measures exhibit persistent intermittent signatures. The scaling exponents derived from cosine-angle increments deviate from those for longitudinal structure functions, emphasizing stronger intermittent trends.

Multiscaling and Probability Distributions

The paper further explores multiscaling through extended self-similarity (ESS), which aids in identifying more pronounced patterns than direct fits could reveal. By analyzing probability distribution functions (PDFs) of the increments themselves, non-Gaussian tails are evident, highlighting extreme fluctuations and reinforcing multiscaling.

Figure 3: Representative plots of PDFs for various increments, exhibiting non-Gaussian tails indicative of multiscaling.

The paper contrasts the geometric contributions to longitudinal and transverse measurements, uncovering a unique domain of scaling exponents tied to flow geometry.

Implications and Future Developments

The findings suggest that conventional approaches to turbulence might be overlooking critical intermittent dynamics inherent to geometric factors. This poses intriguing implications for the paper of turbulent phenomena in fluid dynamics and potentially extends to other fields where complex geometric configurations impact system behavior.

Future research could explore the broader implications of these findings in diverse applications, such as atmospheric sciences or industrial fluid processes. Understanding the geometric contributions to intermittency may lead to improved predictive models and control strategies in turbulent systems.

Conclusion

The investigation presented in "Geometric Intermittency in Turbulence" offers a compelling case for revisiting conventional methodologies in turbulence research. By embracing geometric factors, the paper uncovers a rich tapestry of multiscaling previously hidden in inverse cascade regimes, thus broadening the horizons for future exploration in turbulent dynamics and statistical physics.