MoEGCL: Mixture of Ego-Graphs Contrastive Representation Learning for Multi-View Clustering (2511.05876v1)

Abstract: In recent years, the advancement of Graph Neural Networks (GNNs) has significantly propelled progress in Multi-View Clustering (MVC). However, existing methods face the problem of coarse-grained graph fusion. Specifically, current approaches typically generate a separate graph structure for each view and then perform weighted fusion of graph structures at the view level, which is a relatively rough strategy. To address this limitation, we present a novel Mixture of Ego-Graphs Contrastive Representation Learning (MoEGCL). It mainly consists of two modules. In particular, we propose an innovative Mixture of Ego-Graphs Fusion (MoEGF), which constructs ego graphs and utilizes a Mixture-of-Experts network to implement fine-grained fusion of ego graphs at the sample level, rather than the conventional view-level fusion. Additionally, we present the Ego Graph Contrastive Learning (EGCL) module to align the fused representation with the view-specific representation. The EGCL module enhances the representation similarity of samples from the same cluster, not merely from the same sample, further boosting fine-grained graph representation. Extensive experiments demonstrate that MoEGCL achieves state-of-the-art results in deep multi-view clustering tasks. The source code is publicly available at https://github.com/HackerHyper/MoEGCL.

• The paper introduces MoEGCL, which uses a Mixture-of-Experts for sample-level ego graph fusion and a novel cluster-aware contrastive learning strategy.
• It leverages the MoEGF module to adaptively weight per-sample, per-view ego graphs, significantly improving clustering accuracy over fixed view-level fusion.
• Empirical evaluations on standard multi-view datasets validate the method’s enhanced performance, robust convergence, and low hyperparameter sensitivity.

Mixture of Ego-Graphs Contrastive Representation Learning for Multi-View Clustering

Introduction and Problem Formulation

The paper introduces Mixture of Ego-Graphs Contrastive Representation Learning (MoEGCL), a novel deep multi-view clustering framework targeting the limitations of coarse-grained graph fusion in state-of-the-art multi-view clustering (MVC) approaches. Traditional deep MVC methods generally construct a separate graph for each view and subsequently perform weighted fusion at the view-level, leading to fixed view-dependent coefficients and limited adaptability to sample-specific heterogeneity. MoEGCL addresses this via sample-level, adaptive, fine-grained fusion of ego graphs, leveraging Mixture-of-Experts (MoE) modeling for adaptive weighting, and proposes a bespoke contrastive learning module aligned with sample clusters rather than just individual alignments.

Architectural Innovations: MoEGF and EGCL

The core contributions of MoEGCL are twofold: the Mixture of Ego-Graphs Fusion (MoEGF) module and the Ego Graph Contrastive Learning (EGCL) module.

The MoEGF module first constructs ego graphs for each sample in every view. These ego graphs encode the local neighborhood structure in their respective data modalities (or views), capturing fine-grained, locality-preserving dependencies.

Figure 1: MoEGF builds per-sample, per-view ego graphs, performs sample-level MoE-based fusion weighted by a learned gating network, and aggregates to a global graph structure.

Within the MoEGF, each sample is represented by its ego graphs across all views. The MoE gating network assigns an importance weight to each expert (ego graph from a view), enabling view-adaptive, sample-specific fusion. The fused adjacency vectors are aggregated to form a global adjacency matrix, resulting in a fully connected fused graph reflecting heterogeneous local relationships.

This fused structure is then propagated through a two-layer Graph Convolutional Network (GCN), yielding improved topological feature embeddings that drive downstream clustering.

The EGCL module, in contrast to prior sample-level contrastive approaches, aligns the fused graph representation not just with the same-sample view-specific embeddings, but rather maximizes representation similarity among samples within the same cluster. The operational contrastive loss employs the cluster structure in the denominator, directly enforcing cluster consistency and leveraging the fused adjacency matrix for sample-pair relevance.

Figure 2: Overall MoEGCL architecture, with sample-level ego graph construction and MoEGF fusion preceding cluster-aware contrastive learning in EGCL.

Implementation Details

• Ego Graph Construction: For each sample in each view, construct a $k$-NN based adjacency vector. All ego graphs are represented as rows of the adjacency matrix $S^m$ for each view $m$.
• MoE Gating Network: Concatenate sample representations from all views. Utilize an MLP followed by a softmax to yield a per-sample view weight vector $\mathcal{C}_i$; these coefficients weight the ego graphs at the sample level.
• Fusion and GCN: Generate fused adjacency matrix $S$ by weighted summation (Equation 9 in the paper), add self-loops, and propagate through a GCN layer:

$$\tilde{Z} = (\tilde{D}^{-1/2}\tilde{S}\tilde{D}^{-1/2}) (\cdots)ZW^0 ]W^1$$

• Contrastive Loss: Reduce GCN output and view-specific representations to a latent space via MLPs; similarity is computed via cosine. The loss ensures high similarity for samples in the same cluster (as indicated by $S_{ij}$), with negative terms weighted by $1-S_{ij}$ (Equation 17).
• Training Procedure: A two-phase schedule with 200 pretrain epochs (autoencoder reconstruction only) and 300 fine-tune epochs (joint loss), using batch size 256 and learning rate 0.0003. Hardware utilized: Intel Xeon Platinum 8358 CPU, Nvidia A40 GPU.
• Clustering: Final embeddings are clustered by k-means on the fused representation.

Experimental Analysis

Performance Evaluation

MoEGCL is benchmarked on six standard multi-view datasets (Caltech5V, WebKB, LGG, MNIST, RBGD, LandUse) versus eight advanced baselines (DEMVC, DSMVC, DealMVC, GCFAggMVC, SCMVC, MVCAN, ACCMVC, DMAC). Across all three standard metrics—unsupervised clustering accuracy (ACC), normalized mutual information (NMI), and purity (PUR)—MoEGCL achieves consistent and sometimes substantial improvements over existing methods.

Notably, on WebKB, MoEGCL surpasses ACCMVC in clustering accuracy by 8.19%, with similar trends in NMI and PUR. On RGBD, it outperforms MVCAN by 4.28% ACC, and on more challenging datasets such as Caltech5V, it holds a clear margin.

Ablation and Component Analysis

Ablation studies confirm the distinct contributions of each architectural component. Removal of the MoEGF module ('w/o MoEGF') causes major degradation (up to 40.92% ACC drop, e.g., on WebKB). Omitting the EGCL module or the MoE adaptivity also results in clear performance loss, empirically validating that both fine-grained fusion and cluster-level contrastive alignment are essential.

Representation Visualization

t-SNE projections of embeddings (Figure 3) after MoEGCL training reveal nearly complete separation among clusters, underscoring the discriminative power of the fused, cluster-level representations.

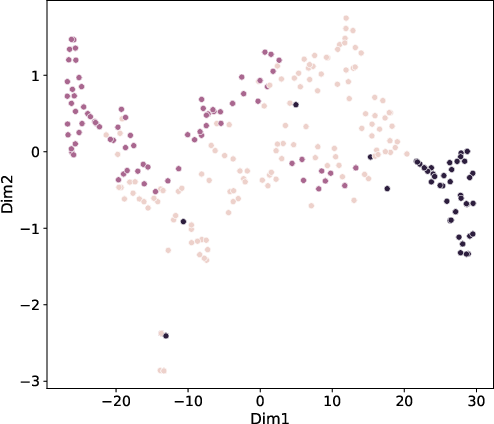
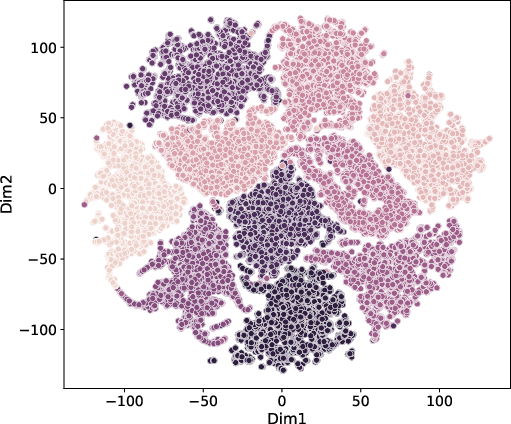
Figure 3: t-SNE visualization of MoEGCL fused graph embeddings on LGG, MNIST, and Caltech5V. Cluster boundaries are well-separated post-convergence.

Convergence and Hyperparameter Stability

Training curves (Figure 4) illustrate stable optimization, with loss plateauing and metrics stabilizing after approximately 400 epochs on Caltech5V. Hyperparameter sweeps (Figure 5) demonstrate minimal sensitivity to the loss balancing parameter $\lambda$ and the contrastive temperature $\tau$, indicating MoEGCL’s robustness and ease of tuning for different datasets.

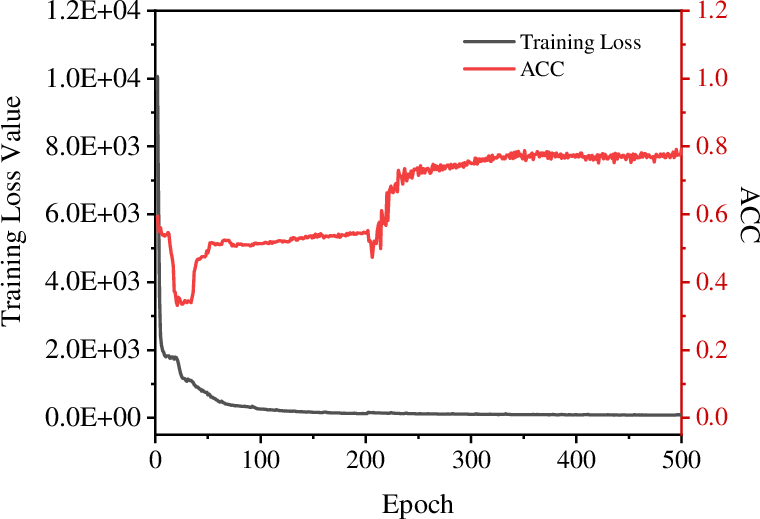
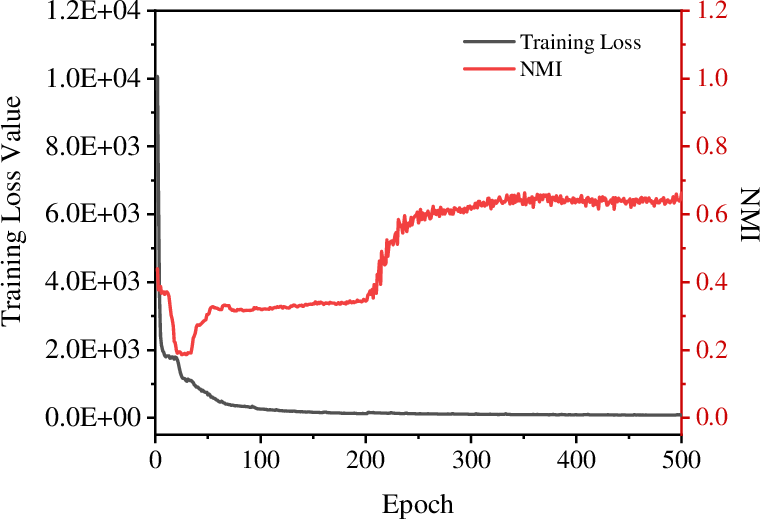
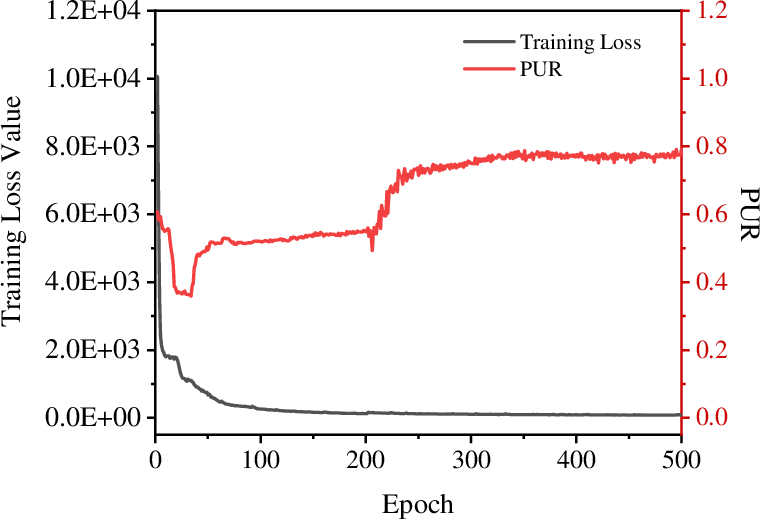
Figure 4: MoEGCL convergence on Caltech5V: ACC, NMI, PUR, and loss curves converge smoothly with minimal overfitting.

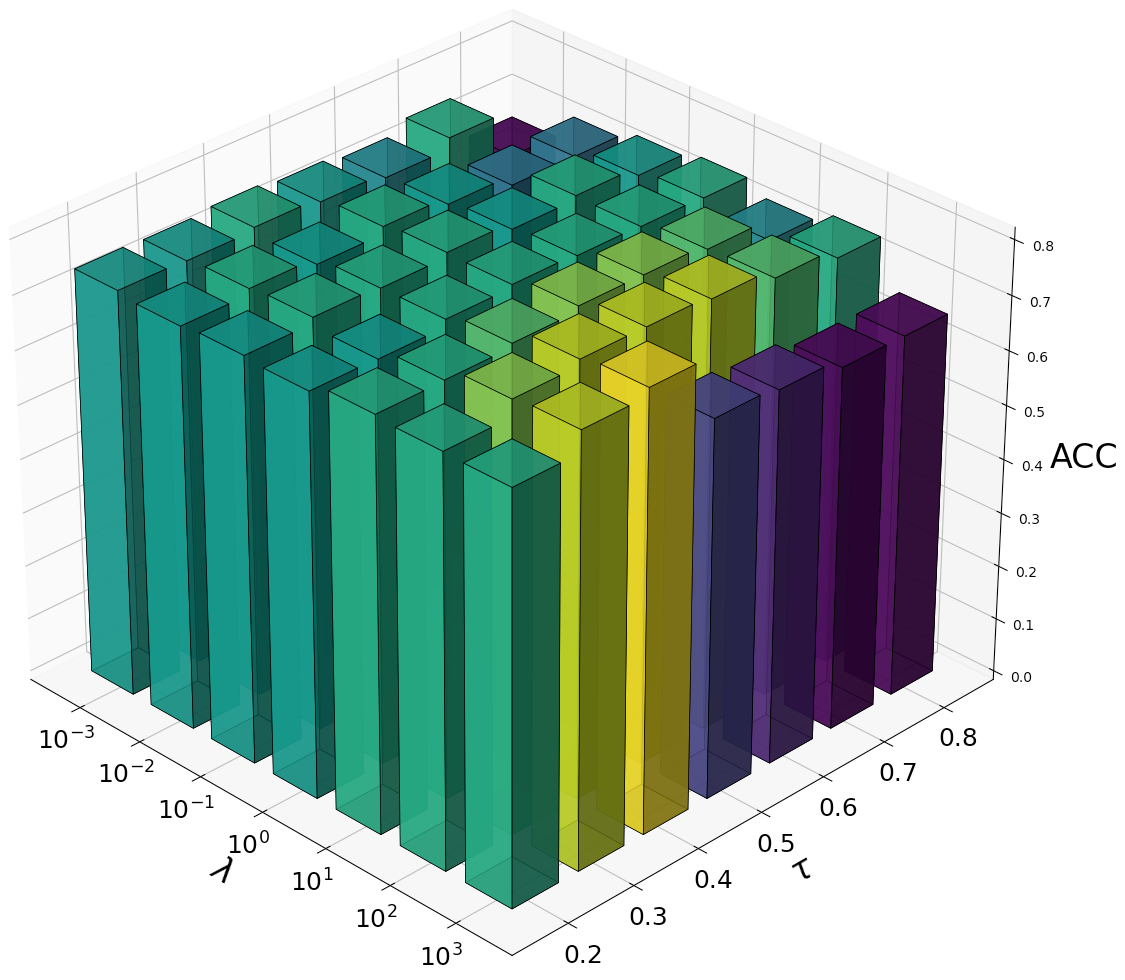
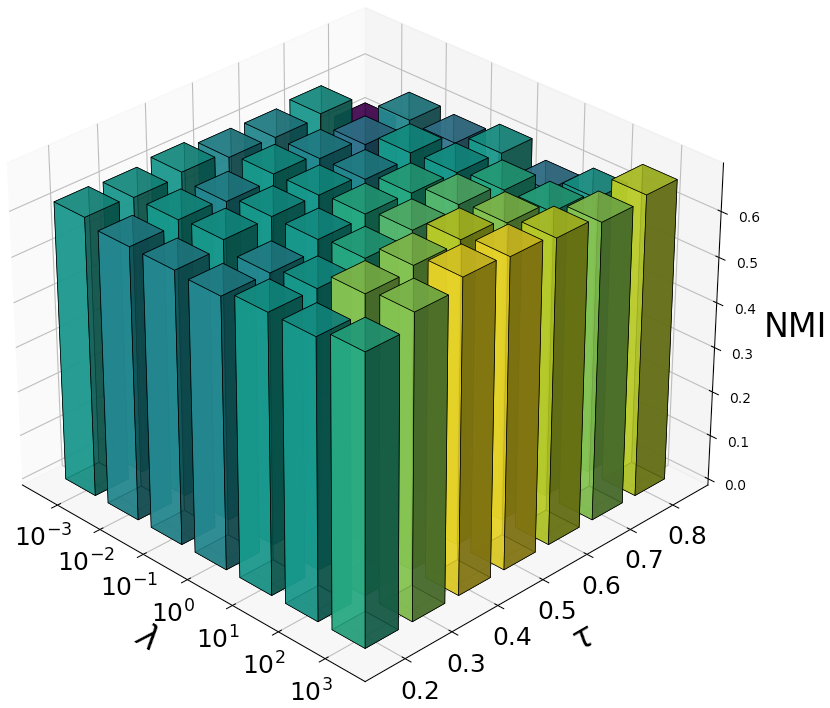
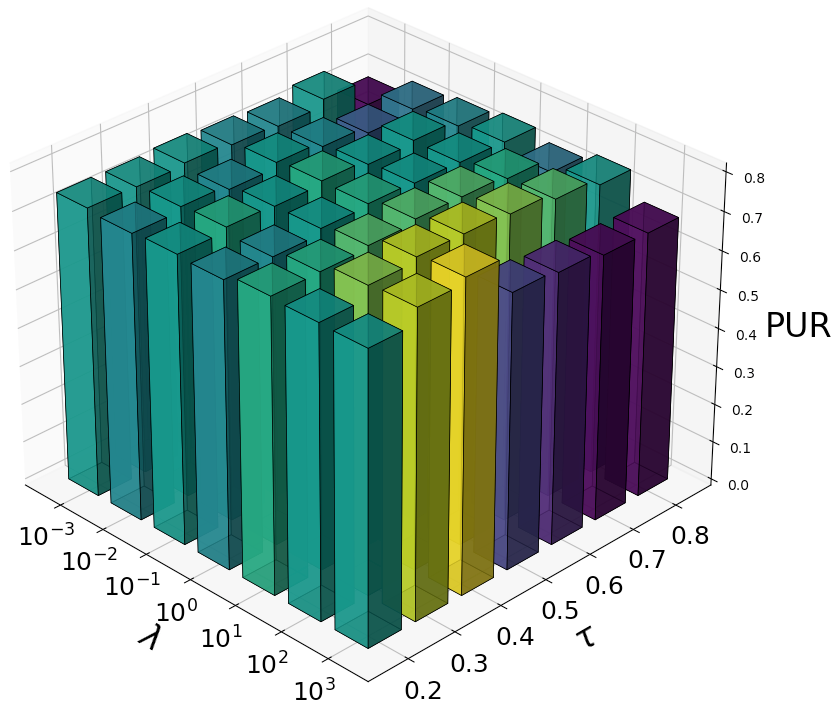
Figure 5: Evaluation metric stability across $\lambda$ and $\tau$ ranges on Caltech5V, highlighting low hyperparameter sensitivity.

Theoretical and Practical Implications

The MoEGCL framework establishes the efficacy of fine-grained, adaptive ego-graph fusion for deep clustering in heterogeneous multi-view settings. By eschewing fixed, view-level graph fusion in favor of dynamic, sample-dependent weighting, it captures cross-view sample-specific heterogeneity, a recurrent challenge in multi-view and multimodal learning.

The cluster-level contrastive learning paradigm introduced by EGCL departs from the standard per-sample view alignment, enforcing cluster consistency and leading to more semantically meaningful and discriminative embeddings. The approach is agnostic to the number of views and robust to data scale—e.g., results on the large MNIST dataset reveal scalability with negligible degradation.

From an application perspective, the methodology is immediately applicable to any domain with multi-modal or multi-view data—medical diagnostics, remote sensing, social network analysis, and multimedia content mining—where local relationships and view-adaptive feature integration are critical.

Limitations and Future Work

Despite strong empirical results, computational complexity can be significant for extremely large datasets due to adjacency matrix operations and per-sample gating. Optimization of scalable MoE architectures or integration with sparse GNN paradigms could further enhance applicability in production-scale settings. Additionally, incorporating domain-specific inductive biases into the gating network or fusing with hierarchical MoE models are promising directions, as is extension to semi-supervised or downstream predictive tasks.

Conclusion

MoEGCL introduces a principled and empirically validated framework for deep multi-view clustering, substantially advancing fine-grained adaptive fusion and cluster-level alignment. Extensive evaluation demonstrates strong, robust improvements, and thorough ablation clarifies the source of its gains. MoEGCL thus offers a methodologically sound and practical advance for multi-modal data analysis, with broad applicability and extensibility to future tasks and domains.