Synthetic Parallel Trends (2511.05870v1)

Abstract: Popular empirical strategies for policy evaluation in the panel data literature -- including difference-in-differences (DID), synthetic control (SC) methods, and their variants -- rely on key identifying assumptions that can be expressed through a specific choice of weights $ω$ relating pre-treatment trends to the counterfactual outcome. While each choice of $ω$ may be defensible in empirical contexts that motivate a particular method, it relies on fundamentally untestable and often fragile assumptions. I develop an identification framework that allows for all weights satisfying a Synthetic Parallel Trends assumption: the treated unit's trend is parallel to a weighted combination of control units' trends for a general class of weights. The framework nests these existing methods as special cases and is by construction robust to violations of their respective assumptions. I construct a valid confidence set for the identified set of the treatment effect, which admits a linear programming representation with estimated coefficients and nuisance parameters that are profiled out. In simulations where the assumptions underlying DID or SC-based methods are violated, the proposed confidence set remains robust and attains nominal coverage, while existing methods suffer severe undercoverage.

• The paper introduces the Synthetic Parallel Trends (SPT) framework that unifies difference-in-differences and synthetic control by leveraging weighted pre-treatment trends to identify counterfactual outcomes.
• The methodology uses linear programming to construct identified sets for treatment effects, allowing for both point and interval identification depending on the data generating process.
• Simulation studies demonstrate that SPT delivers robust inference and adapts to model uncertainty, outperforming traditional methods in complex panel data settings.

Synthetic Parallel Trends: A Unifying, Robust Framework for Panel Data Treatment Effect Identification

Introduction and Motivation

The "Synthetic Parallel Trends" paper (2511.05870) addresses a central challenge in causal inference using panel data: identification of counterfactual outcomes under intervention. The canonical approaches—difference-in-differences (DID), synthetic control (SC), and their variants (e.g., two-way fixed effects (TWFE), synthetic DID (SDID))—rely on key identifying assumptions that can each be expressed as imposing a specific choice of weights $\omega$ to relate pre-treatment trends of treated and control units to the unobserved treated potential outcome in the post-treatment period.

Each method's identifying assumption is strong and fundamentally untestable, leading to a risk of severe bias or undercoverage when violated. In response, the paper proposes the Synthetic Parallel Trends (SPT) assumption: it requires only that some (potentially unknown) weighted combination of control unit pre-treatment trends matches the treated unit's pre-treatment trend, and posits that these same weights can be used to construct an identified set for the unobserved post-treatment counterfactual. By considering all such weights rather than a single estimand-specific set, the SPT framework nests DID and SC as special cases, yielding identification and inference procedures that are inherently robust to violations of any method’s particular set of assumptions.

Formal Framework and Main Contributions

Synthetic Parallel Trends (SPT) Assumption

The SPT assumption requires existence of a set of weights $\omega$ (affine or convex, with $\sum \omega_k = 1$) such that for all pre-treatment periods, the treated unit's trend matches the weighted aggregate of control units’ trends. In matrix form, these weights are solution(s) to a system of (typically underdetermined) linear equations:

$A^{\mathrm{pre}} \omega = b^{\mathrm{pre}}$,

where $A^{\mathrm{pre}}$ comprises stacked control unit pre-trends and $b^{\mathrm{pre}}$ is the treated unit's pre-trend vector.

Identification of the counterfactual trend in the post-treatment period $\Delta \mu_T^1(0)$ is then given by the set:

$$M = \{\mathbf{a}' \omega : \omega \in \mathbb{R}^{K-1}, \mathbf{1}' \omega = 1, A^{\mathrm{pre}} \omega = b^{\mathrm{pre}} \}$$,

where $\mathbf{a}$ is the vector of observed control unit post-treatment trends. When further restricting the weights to be nonnegative (convex combination), the identified set is:

$$M^+ = \{\mathbf{a}' \omega : \omega \in \mathbb{R}_+^{K-1}, \mathbf{1}' \omega = 1, A^{\mathrm{pre}} \omega = b^{\mathrm{pre}} \}$$.

This approach leads to partial identification—the identified set may be an interval, possibly a singleton (point identification), or unbounded (no informative identification) depending on the properties of the data generating process (DGP) and the empirical content of the assumptions.

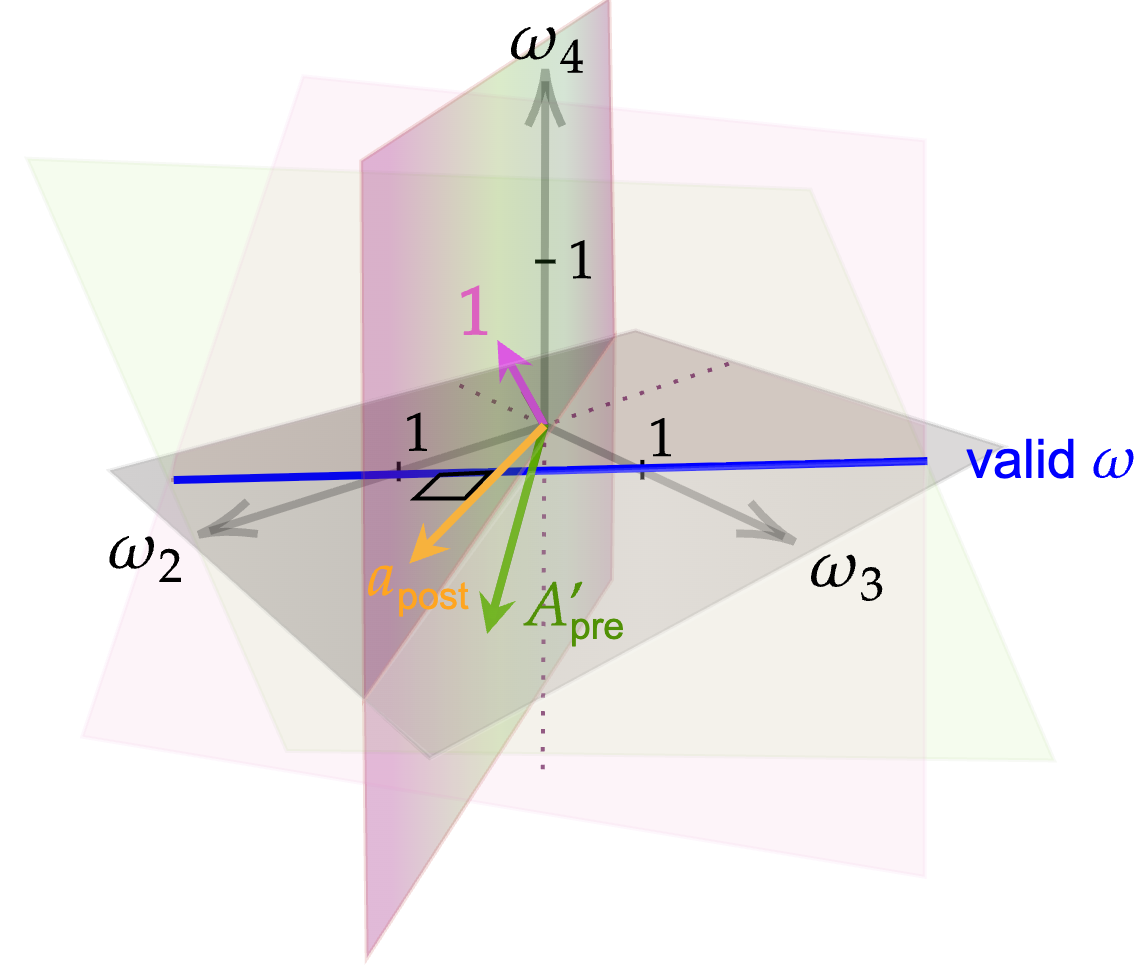
Figure 1: Necessary and sufficient condition for point identification under Assumption \ref{asm:spt}.

Connection With DID and SC: Weighting as Unifying Principle

DID and SC both produce point estimates by implicitly or explicitly selecting a unique $\omega$ (e.g., population shares in DID, balancing weights in SC). The SPT framework reveals that these familiar estimators just correspond to specific solutions within the broader identified set $M^+$, with their validity hinging on whether the pre-trend system identifies a unique or credible $\omega$. SPT thus provides a unified perspective, clarifying both the fragility and context-dependence of widely used estimators.

• Under low-rank DGPs (e.g., TWFE), the identified set collapses to a point (singleton), and all methods agree.
• Under model violations or increased heterogeneity, the system is underdetermined; the identified set widens, and robust inference must reflect this increased uncertainty.

Linear Programming Characterization and Partial Identification

SPT identification regions (the sets $M$ and $M^+$) can be represented as solutions to linear programs (LPs) with affine equality (and optionally nonnegativity) constraints on the weights. For practical inference, these LPs can be solved efficiently for lower and upper bounds of the identified interval:

$$M^+ = [\mu_l^+, \mu_u^+] = [\min_{\omega \in \Delta^{K-2}} \mathbf{a}'\omega, \ \max_{\omega \in \Delta^{K-2}} \mathbf{a}'\omega]$$

where $\Delta^{K-2}$ is the unit simplex defined by nonnegativity and sum-to-one constraints, and the pre-trend balancing constraints.

If the solution space is a singleton—i.e., when the post-trend vector is an affine function of the pre-trends—point identification results. Otherwise, the identified set is an interval reflecting partial identification and model uncertainty.

Inference Under Partial Identification: Profiling and Test Inversion

The paper develops a valid, computationally tractable confidence set for the partially identified treatment effect using test inversion and profile minimization. The resulting estimator profiles over all feasible weight vectors $\omega$ (within the simplex) that satisfy the pre-trend balancing conditions:

• Formulate the constraints as a quadratic program for the treatment effect, profiling out the high-dimensional nuisance parameter $\omega$.
• Use test inversion to construct a confidence set for the scalar treatment effect parameter, ensuring robust nominal coverage even when parallel trends or SC assumptions fail.
• The approach accommodates both panel and repeated cross-section designs, and the confidence set adapts to uncertainty in the identification power of the data and the assumptions.

Statistical inference is based on Hadamard directionally differentiable mappings for the profiled quadratic criterion. The limit distribution is approximated via specialized bootstrap techniques that preserve the partial identification structure and cope with non-differentiability (standard nonparametric bootstrap is inconsistent).

Empirical Illustration and Simulation

Comprehensive simulations on panel and repeated cross-sectional data (including data-generating processes with known violations of the DID and SC assumptions) demonstrate the robustness and informativeness of SPT-based identification and inference. In scenarios where DID or SC perform poorly (e.g., severe undercoverage due to invalid identifying assumptions), SPT confidence sets maintain the correct nominal coverage; though the identified intervals may be wider, they remain informative in empirical designs where previous methods break down.

Theoretical and Practical Implications

• Unification of Existing Methods: The SPT framework formalizes and generalizes the implicit weighting foundations of DID, SC, and their hybrids. It makes explicit the untestable but critical identifying assumptions underlying these estimators.
• Intrinsic Robustness: By embracing the partial identification approach, SPT yields valid inferential guarantees even in settings where existing estimators are fragile, including when only weak or plausible constraints can be defended.
• Operational Efficiency: Representing the identified set via LPs (with optional convexity constraints on $\omega$) enables fast and scalable computation for both identification and inference, with computational burdens growing polynomially in the sample/panel size.
• Testability of Assumptions: Assumptions regarding weight convexity, model low-rankness, or support can be empirically falsified via feasibility checks on the LP constraints or rank tests, providing a diagnostic toolkit for applied researchers.
• Relevance for Policy Evaluation: The framework is particularly powerful in situations with many control units, short panels, or complex unobserved heterogeneity, which are prevalent in cross-jurisdiction policy or intervention studies.

Future Research Directions

Extensions naturally include incorporating covariate balance constraints, exploring efficient weighting and estimation strategies for the profile criterion, generalizing to settings with staggered treatments or time-varying exposure, and studying uniform (as opposed to pointwise) validity of inferential procedures. The approach also opens new avenues for sensitivity analysis and formalizes a partial identification paradigm for panel data settings beyond synthetic controls.

Conclusion

The "Synthetic Parallel Trends" paper establishes a rigorous partial identification and inference framework that synthesizes and strengthens the foundations of leading empirical methodologies for panel data treatment effect evaluation. By revealing the common underlying weighting logic, formalizing robust identification sets via LPs, and providing valid inference under minimal assumptions, the SPT approach equips researchers with a more general and defensible toolkit for causal inference in complex panel data settings.

This theoretical development carries practical importance for empirical program evaluation, especially where standard identifying assumptions are suspect or only approximate, and sets an agenda for future research integrating identification, diagnostic, and inference tools in applied econometrics and causal inference.