Forgetting is Everywhere (2511.04666v1)
Abstract: A fundamental challenge in developing general learning algorithms is their tendency to forget past knowledge when adapting to new data. Addressing this problem requires a principled understanding of forgetting; yet, despite decades of study, no unified definition has emerged that provides insights into the underlying dynamics of learning. We propose an algorithm- and task-agnostic theory that characterises forgetting as a lack of self-consistency in a learner's predictive distribution over future experiences, manifesting as a loss of predictive information. Our theory naturally yields a general measure of an algorithm's propensity to forget. To validate the theory, we design a comprehensive set of experiments that span classification, regression, generative modelling, and reinforcement learning. We empirically demonstrate how forgetting is present across all learning settings and plays a significant role in determining learning efficiency. Together, these results establish a principled understanding of forgetting and lay the foundation for analysing and improving the information retention capabilities of general learning algorithms.
Summary
- The paper's main contribution is a predictive formalism that defines forgetting as a divergence between induced future distributions before and after updates.
- It operationalizes forgetting using the k-step propensity measure, validated empirically across regression, classification, generative, continual, and reinforcement learning tasks.
- Empirical findings reveal a trade-off where moderate forgetting enhances learning efficiency, while excessive forgetting destabilizes training and impairs adaptation.
Forgetting is Everywhere: A Predictive Theory and Empirical Analysis
Introduction
The paper "Forgetting is Everywhere" (2511.04666) presents a unified, predictive theory of forgetting in machine learning, applicable across supervised, generative, and reinforcement learning paradigms. The authors formalise forgetting as a violation of self-consistency in a learner's predictive distribution over future experiences, rather than as a mere drop in performance or memorisation. This approach enables a principled, operational measure of a learner's propensity to forget, which is empirically validated across diverse learning scenarios. The work provides both theoretical and practical insights into the dynamics of information retention and loss, revealing that forgetting is a pervasive and often necessary aspect of efficient learning.
Predictive Formalism and Consistency
The core theoretical contribution is the predictive formalism, which models learning as a stochastic interaction between a learner and its environment. The learner's internal state evolves via updates, inducing a predictive distribution over possible future histories. Forgetting is defined as the divergence between the induced futures before and after updates on data consistent with the learner's own predictions. If updating on expected data alters the induced futures, the learner is said to forget.
Figure 1: State evolution and induced futures. The learner's internal state evolves through training updates, each inducing a distribution over possible future interactions.
This formalism generalises across learning paradigms by abstracting observations, predictions, and state updates. The consistency condition requires that, in expectation, the learner's induced futures remain invariant under updates on self-consistent data. Violation of this condition quantifies forgetting.
Operational Measure: Propensity to Forget
The paper introduces the -step propensity to forget, , defined as the divergence between the initial induced futures and those after updates on self-consistent data. This measure is operationalised via Monte Carlo rollouts, cloning the learner and simulating updates to estimate the divergence empirically.
Figure 2: Information absorption and loss over a single learning update. Each update assimilates new information and displaces part of the prior state, resulting in a new predictive distribution.
This approach distinguishes forgetting from backward transfer and performance fluctuations, focusing on the loss of predictive capabilities rather than memorisation or accuracy. The measure applies to any learner whose state induces a coherent predictive distribution, encompassing parametric, non-parametric, and Bayesian models.
Empirical Characterisation Across Learning Paradigms
Extensive experiments demonstrate that forgetting is ubiquitous in deep learning, manifesting in regression, classification, generative modelling, continual learning (CL), and reinforcement learning (RL). The dynamics and magnitude of forgetting vary with the learning paradigm, model architecture, and hyperparameters.
Figure 3: Forgetting occurs across all deep learning scenarios. Forgetfulness profiles for regression, classification, and generative modelling tasks, and abrupt increases at task boundaries in class-incremental learning.
Key findings include:
- Non-zero Forgetting in All Settings: Forgetting is present even in stationary, i.i.d. environments, not just in CL or RL.
- Trade-off with Training Efficiency: Moderate forgetting improves learning efficiency; too little slows adaptation, too much destabilises learning.
- Distribution Shift Effects: CL and RL exhibit abrupt or chaotic forgetting dynamics due to non-stationarity, reducing training efficiency.
- Algorithmic and Architectural Influences: Model size, momentum, batch size, and architecture all modulate forgetting dynamics.
Figure 4: Approximate learners can benefit from non-zero forgetting. Training efficiency peaks at moderate levels of forgetfulness, indicating a fundamental trade-off.
Figure 5: Chaotic forgetting dynamics in RL. RL learners display persistent, chaotic fluctuations in forgetting due to environmental non-stationarity.
Theoretical Implications and Boundary Conditions
The predictive formalism delineates the conditions under which forgetting is well-defined. Learners must induce a coherent predictive distribution over futures; during transitory phases (e.g., buffer resets, target network lag), this mapping may be undefined. Replay mechanisms theoretically restore conditional independence, mitigating forgetting when the update function depends on history.
Bayesian learners exemplify self-consistency: exact Bayesian updates are permutation-invariant and do not forget, as their induced futures remain recoverable by marginalisation. Approximate inference and gradient-based updates violate self-consistency, leading to order-dependent forgetting.
Figure 6: Self-consistent learners do not forget. Bayesian posteriors are invariant to data order, while approximate learners lose predictive capabilities.
Hyperparameter and Architecture Effects
Empirical analysis reveals nuanced effects of model and optimisation choices:
- Model Size: Forgetting increases with parameter count up to the task's effective complexity, then decreases in overparameterised regimes.
- Momentum: Higher momentum amplifies periodic forgetting oscillations; optimal efficiency occurs at intermediate values.
- Batch Size: Small batches induce high variability and greater forgetting; larger batches stabilise learning but do not eliminate forgetting.
- Architecture: Deep models (CNNs, ResNets) exhibit higher forgetting yet achieve superior generalisation, indicating that minimising forgetting is not always optimal.
Figure 7: Impact of model size on forgetting dynamics. Forgetting peaks near the effective task complexity.
Figure 8: Effect of the momentum parameter on forgetting dynamics. Periodicity and amplitude of forgetting increase with momentum.
Figure 9: Effect of batch size on forgetting dynamics. Larger batches stabilise learning and reduce forgetting.
Figure 10: Forgetting dynamics across model architectures. Deep models forget more but generalise better.
Practical and Theoretical Implications
The predictive theory of forgetting provides a principled framework for analysing information retention and loss in general learning systems. The operational measure enables empirical validation and comparison across algorithms and settings. The identification of a trade-off between forgetting and efficiency suggests that optimal learning requires regulated, non-zero forgetting, challenging the notion that perfect memory is always desirable.
In RL and CL, the theory highlights the need for algorithms that stabilise forgetting dynamics under non-stationarity. Replay and regularisation methods can be theoretically justified as mechanisms to restore predictive consistency. The framework also clarifies the distinction between constructive adaptation (backward transfer) and destructive forgetting, informing the design of continual and lifelong learning systems.
Future Directions
Potential future developments include:
- Algorithmic Design: Developing learning algorithms that explicitly regulate forgetting to optimise efficiency and stability.
- Replay Mechanisms: Theoretical analysis and empirical validation of replay strategies in restoring predictive consistency.
- Extension to Large-Scale Models: Application of the forgetting measure to LLMs and foundation models, investigating scaling laws and retention dynamics.
- Unlearning and Privacy: Leveraging the formalism for principled machine unlearning, where controlled forgetting is required for privacy or compliance.
Conclusion
"Forgetting is Everywhere" establishes a predictive, task-agnostic theory of forgetting, supported by a robust operational measure and comprehensive empirical analysis. The work demonstrates that forgetting is a fundamental, pervasive aspect of learning, shaped by the interaction between adaptation and retention. Efficient learning requires not the absence of forgetting, but its principled regulation. This perspective provides a foundation for future research into the dynamics of information retention, continual adaptation, and the development of more robust learning algorithms.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
A simple explanation of “Forgetting is Everywhere”
Overview
This paper studies a common problem in machine learning called forgetting. Just like a student who learns new topics and accidentally forgets old ones, computer models can lose what they learned earlier when they update themselves with new data. The authors offer a simple, general way to define and measure forgetting that works across many kinds of AI systems, from image classifiers to game-playing agents. They also show, with lots of experiments, that forgetting happens almost everywhere—and that a small amount of forgetting can actually help models learn faster.
What questions does the paper ask?
To make the idea clear for everyone, the paper focuses on a few basic questions:
- What exactly is “forgetting” for a learning algorithm?
- How can we tell if a model has forgotten something, without mixing it up with other effects (like when new learning actually helps old skills)?
- Can we measure a model’s tendency to forget in a fair and general way?
- How common is forgetting in different types of AI (like classification, regression, generative models, and reinforcement learning)?
- How does forgetting affect how quickly and well models learn?
How did they paper it? (Methods in everyday language)
The authors define learning as an ongoing back-and-forth between a learner (the model) and its environment (the data or world it interacts with). Think of it like this:
- The learner sees something (an input), makes a choice or a prediction (an output), and then updates itself based on what happened.
Here’s the key idea they use to define forgetting:
- Imagine the learner “daydreams” about the future. From its current knowledge, it can play a mental movie of what it expects to happen next: what inputs it might see and what predictions it would make. The paper calls this an “induced future.” It’s like the model pressing fast-forward in its head without getting new real data.
- Now, suppose the learner gets exactly the kind of data it already expected. If it still changes its future predictions after updating, that change can’t be new learning—because nothing surprising happened. It must be forgetting something it already knew.
So, the paper defines forgetting as a loss of self-consistency in the learner’s predictions over time. If predictions drift when nothing new was learned, that’s forgetting.
To turn this into a measurement, they compare:
- The learner’s predicted “mental future” before an update, and
- The learner’s predicted “mental future” after a few steps of updates on data it already expected.
The bigger the difference between these two futures, the stronger the “propensity to forget.” You can think of this number as “how much the model’s future story changed when nothing surprising happened.”
What did they find, and why is it important?
Across many kinds of AI tasks, they found that forgetting:
- Happens in lots of places, not just in special “continual learning” setups. Even in standard training with shuffled data, models can forget.
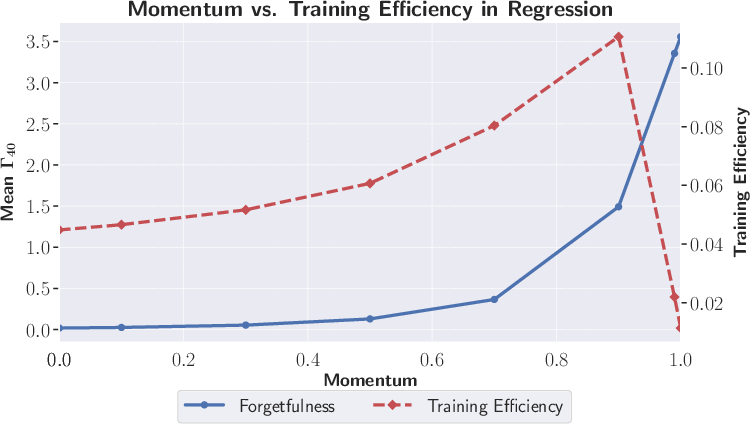
- Often shows a trade-off with learning speed. Surprisingly, a little bit of forgetting can help a model adapt faster. Too little forgetting makes the model slow to change; too much makes it unstable.
- Spikes when the data suddenly changes (like when you switch tasks). This matches what you’d expect: big shifts force big updates, which can erase earlier knowledge.
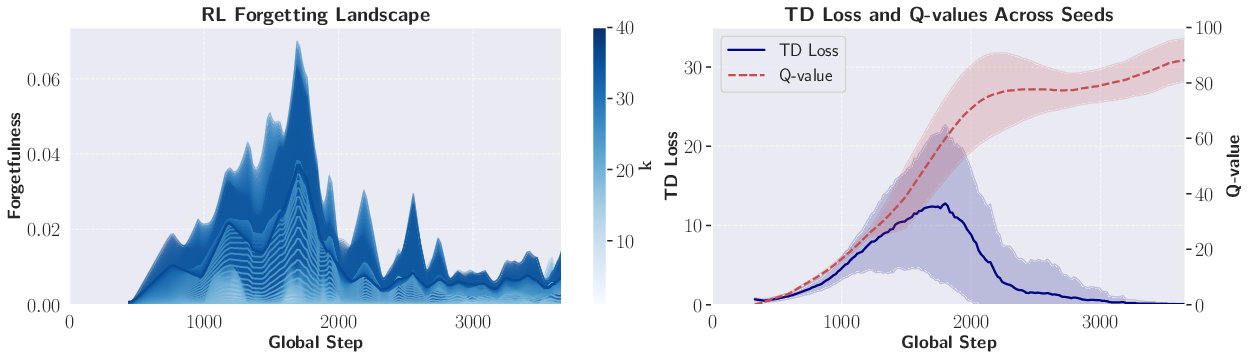
- Is especially chaotic in reinforcement learning (RL). In RL, the model’s own behavior changes the data it sees, so the training never really settles down. This leads to unstable patterns of forgetting and can hurt learning efficiency.
Why this matters:
- The paper’s definition separates true forgetting (loss of stored knowledge) from good effects like “backward transfer” (where learning something new accidentally improves old skills). That makes it easier to diagnose what’s really going on during training.
- A clear, general measure helps compare algorithms and choose settings (like model size or momentum) that balance adaptation and memory.
- Understanding forgetting better could lead to AI that keeps old skills while learning new ones—like a student who can add new chapters to their notebook without erasing the earlier ones.
What could this change in the future? (Implications)
- Better diagnostics: Developers can track a model’s “propensity to forget” to spot when updates are erasing useful knowledge, even if accuracy looks fine for now.
- Smarter training: Knowing that some forgetting helps, we can tune models to balance “learn new stuff quickly” with “keep what matters.”
- Stronger algorithms: This predictive, “mental future” view of learning gives a foundation for designing training methods that keep models self-consistent over time, especially in unstable settings like RL.
- Unified research: Because the definition doesn’t depend on a specific task or algorithm, it can guide improvements across classification, regression, generative models, and RL.
In short, the paper shows that forgetting isn’t a rare bug—it’s a normal part of how AI learns. With a clear way to define and measure it, we can build systems that learn faster and forget less of what matters.
Knowledge Gaps
Below is a single, focused list of knowledge gaps, limitations, and open questions that the paper leaves unresolved. Each item is stated concretely to guide follow‑on research.
- Formal definition and construction of the hybrid environment distribution q_e: The paper relies on a “hybrid” q_e that treats the learner’s predictions as targets while “borrowing” unspecified components from the environment, but does not fully specify how q_e should be instantiated across paradigms (supervised, generative, RL), nor the conditions required for its existence and uniqueness.
- Practical estimation of induced future distributions over infinite sequences: The measure compares distributions on futures H{t+k:∞}, but the paper does not provide a general, scalable estimator for these distributions, nor finite‑horizon approximations with provable error bounds or consistency guarantees.
- Choice and properties of the divergence D: The measure depends on a divergence D, yet the paper offers no principled guidance for choosing D across settings (KL, MMD, Wasserstein, f‑divergences), nor analyses of metric sensitivity, invariance, and implications for comparability of Γ_k across domains.
- Sensitivity to horizon k and convergence behavior: There is no analysis of how Γ_k(t) depends on k, whether it stabilizes as k→∞, how to choose k in practice, or what guarantees exist on bias/variance when using finite k.
- Detecting and handling coherence failures: The formalism requires a coherent mapping Z_t ↦ q(H{t+1:∞} | Z_t, H_{0:t}) but does not propose operational tests to detect when coherence fails (e.g., target network lag, buffer resets), nor methods to measure or mitigate forgetting during these non‑coherent phases.
- Separation of forgetting from backward transfer in practice: Although the conceptual setup aims to separate the two, the empirical methodology for ensuring this separation (via q_e and self‑consistent targets) is not fully specified for real data streams, leaving ambiguity in practical measurement.
- Computational tractability and scalability: The paper does not quantify the computational cost of simulating induced futures, estimating divergences, or running the consistency checks, nor provide algorithms that scale to large models and datasets (e.g., foundation models, high‑dimensional RL).
- Generalization of the measure to non‑probabilistic or partially specified learners: The framework excludes learners that do not induce a single coherent predictive model; it remains open how to extend or adapt the measure to ensembles, hybrid symbolic‑neural systems, or algorithms with implicit/approximate predictive states.
- Theoretical guarantees linking consistency violations to performance: While the paper reports empirical correlations, it does not provide formal results connecting Γ_k(t) to generalization error, regret, sample complexity, or convergence properties in standard learning theory.
- Decomposition of forgetting into interpretable components: There is no method to attribute Γ_k(t) to specific mechanisms (e.g., capacity limits, representation drift, buffer eviction, optimizer dynamics), hindering diagnosis and targeted mitigation.
- Robustness to data properties: The impact of label noise, class imbalance, covariate shift, long‑tail distributions, and temporal correlations on Γ_k(t) is not characterized; it remains unclear how data pathologies confound the measure.
- Protocols for RL measurement: The RL experiments highlight chaotic dynamics but do not specify standardized protocols for estimating q_e, induced futures, and Γ_k(t) in policy‑dependent, non‑stationary environments (e.g., off‑policy vs on‑policy, partial observability, reward shaping).
- Effect of standard CL/RL mitigation strategies: The paper does not test whether Γ_k(t) aligns with or predicts the efficacy of replay, regularization (e.g., EWC, LwF), architectural methods, or policy‑stabilization techniques, nor whether Γ_k(t) can guide hyperparameter tuning.
- Cross‑metric validation against established forgetting measures: There is limited empirical validation that Γ_k(t) correlates with or improves upon classical CL metrics (e.g., average accuracy, backward transfer) across diverse benchmarks and algorithms.
- Estimation error and confidence quantification: The paper does not provide statistical procedures (confidence intervals, concentration bounds, bootstrap methods) to quantify uncertainty in Γ_k(t) estimates, especially under stochastic training and policy‑induced non‑stationarity.
- Intervention design to enforce consistency: The work frames forgetting as consistency violation but does not propose algorithmic interventions (penalties, constraints, update rules) that enforce or regularize predictive self‑consistency, nor analyze their trade‑offs.
- Guidelines for hyperparameter selection: The reported “elbow” trade‑off between efficiency and forgetting lacks actionable rules to set optimizer parameters, model capacity, or regularization strength to target desired Γ_k(t) profiles.
- Applicability to large‑scale and multi‑modal models: Experiments are limited to small networks and simple tasks; it remains open whether Γ_k(t) is practical and informative for LLMs, diffusion models, retrieval‑augmented systems, and multi‑modal architectures.
- Transfer across domains and tasks: The measure’s portability to few‑shot, meta‑learning, offline/streaming learning, self‑training, and self‑play scenarios requires further paper and specification.
- Causal analysis of forgetting dynamics: The framework is descriptive; it does not establish causal links between specific updates or data regimes and changes in Γ_k(t), nor propose controlled interventions to isolate causes.
- Benchmarking and reproducibility standards: There is no standardized benchmark suite, logging protocol, or open‑source tooling for measuring Γ_k(t) across settings, impeding systematic comparison and adoption.
- Policy‑induced distribution shift in RL: Open questions remain on how to temporally align Γ_k(t) with policy changes, visitation shifts, and exploration schedules, and how to decouple environment non‑stationarity from learner‑induced forgetting.
- Interaction with representation learning: The paper does not analyze how feature learning, layer‑wise dynamics, or architectural choices (e.g., normalization, residual connections) influence self‑consistency and Γ_k(t).
- Theoretical bounds under idealized learners: It remains unknown whether Bayesian or information‑theoretically optimal learners achieve Γ_k(t)=0 under certain conditions, and what structural constraints (capacity, priors, update rules) are necessary or sufficient for consistency.
Practical Applications
Immediate Applications
Below are concrete, deployable ways to use the paper’s predictive-consistency view of forgetting and the “propensity to forget” measure Γk in products, workflows, and research today.
- Forgetting monitoring in training loops
- What: Add a “Γk meter” to PyTorch/TensorFlow/JAX training callbacks that periodically rolls out short induced futures in inference mode and computes divergences (e.g., KL for classifiers/regressors, MMD for generative models).
- Sectors: Software, AI/ML platforms, academia.
- Tools/products/workflows: Training dashboard panels (“Forgetting Profile”), CI checks that fail runs with spiking Γk, seed-swept reports.
- Assumptions/dependencies: Define inference-mode update u′ (often identity for parameters), choose divergence metric and horizon k, accept extra compute (short k, minibatch sampling mitigate cost), ensure a coherent predictive mapping exists during measurement.
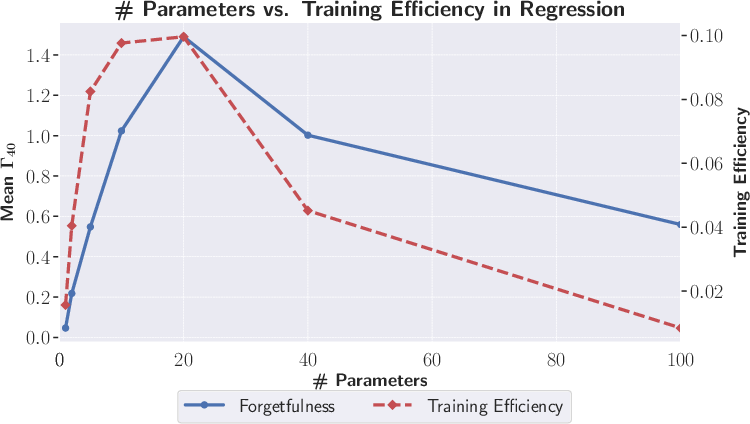
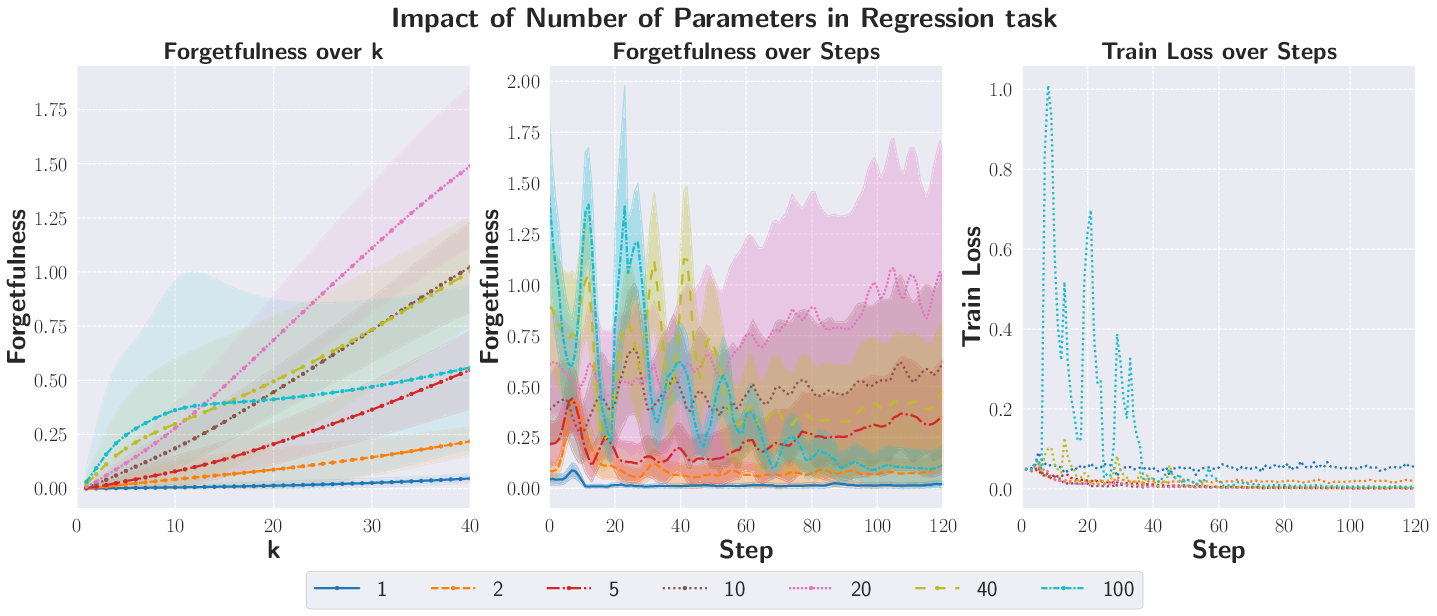
- Hyperparameter tuning via forgetting-efficiency elbow
- What: Use Γk vs. training-efficiency curves to tune momentum, learning rate schedules, batch size, model size to the “elbow” where moderate forgetting maximizes learning speed.
- Sectors: Software/AutoML, academia.
- Tools/products/workflows: Optuna/Weights & Biases sweeps optimizing a scalarized objective (maximize efficiency, constrain mean Γk), AutoML policy “target a Γk band.”
- Assumptions/dependencies: Stable Γk estimates (aggregate over steps/seeds); task-specific divergence.
- Continual learning (CL) evaluation that disentangles backward transfer
- What: Report Γk alongside task accuracy to separate constructive reuse (backward transfer) from destructive adaptation (forgetting).
- Sectors: Academia, software (vision/NLP CL), robotics (lifelong perception).
- Tools/products/workflows: CL benchmark leaderboards adding Γk; paper checklists reporting “Forgetting Profile Cards.”
- Assumptions/dependencies: Per-task or unified interface to compute induced futures; i.i.d. vs task-shift aware q_e design.
- Replay buffer scheduling that reduces forgetting
- What: In DQN/DMC/behavior cloning with replay, adapt sampling weights to minimize recent Γk spikes (e.g., upweight transitions/tasks whose replays lower Γk).
- Sectors: RL, robotics, gaming, energy grid control.
- Tools/products/workflows: “Forgetting-aware PER”: priority = TD-error × (1 + λ·local Γk contribution).
- Assumptions/dependencies: Approximated Γk contributions per batch; inference-mode rollout defined for the agent.
- Early-warning signals for RL instability
- What: Monitor chaotic Γk fluctuations to trigger stabilizers (reduce LR, freeze layers, increase target-network lag, increase replay ratio, broaden data coverage).
- Sectors: RL, robotics, autonomous driving, finance trading agents, operations research.
- Tools/products/workflows: RLlib/Stable-Baselines callbacks that gate updates when Γk exceeds threshold; “stability mode” switch.
- Assumptions/dependencies: Rolling-window Γk; target networks and policy resets can temporarily invalidate coherence—skip or annotate those windows.
- Safer fine-tuning and instruction-tuning of LLMs
- What: Track Γk on capability probe suites (math, code, reasoning) while fine-tuning on new tasks to prevent ability loss; regulate LoRA rank, data mix, or learning rate when Γk rises.
- Sectors: Software, education, enterprise productivity.
- Tools/products/workflows: “Capability Anti-Regression Guardrail” in fine-tuning pipelines; mixing base data to cap Γk.
- Assumptions/dependencies: Probe set reflecting “induced futures” on capabilities; divergence via token-level KL on next-token distributions.
- Generative model self-training/collapse guardrails
- What: During self-distillation or model-on-model training, use Γk to detect self-consistency violations that precede mode collapse; inject real data or regularization when Γk spikes.
- Sectors: Imaging, speech, creative tools.
- Tools/products/workflows: Teacher-student loops with “Γk-triggered refresh” of real samples; MMD- or FID-adjacent divergence for images.
- Assumptions/dependencies: Pragmatic induced future approximation (short rollouts, batch-level MMD/Fisher).
- Curriculum/task ordering that smooths forgetting
- What: Choose task order and mix that minimize abrupt Γk jumps at boundaries; insert buffer phases to re-stabilize futures.
- Sectors: Education tech, CL benchmarks, robotics skill acquisition.
- Tools/products/workflows: Curriculum schedulers optimizing “smooth Γk trajectory” subject to time/accuracy constraints.
- Assumptions/dependencies: Ability to simulate alternative curricula; short-horizon Γk proxy during pilots.
- Slice-aware retention for fairness and robustness
- What: Monitor Γk per data slice (minority class, language, region) to prevent eroding performance on rare groups during updates.
- Sectors: Healthcare, finance, hiring, content moderation.
- Tools/products/workflows: “Retention budgets” per slice; training sampler boosts slices with rising Γk; fairness reports include slice-level Γk trends.
- Assumptions/dependencies: Reliable slice membership; privacy-safe logging; sufficient per-slice support for estimation.
- Online personalization with retention budgets
- What: In recommenders, keyboards, spam filters, and on-device personalization, cap Γk to avoid overfitting to short-term trends while preserving long-term preferences.
- Sectors: Consumer apps, e-commerce, media.
- Tools/products/workflows: Streaming learners with “forgetting governors” (decay LR or freeze layers when Γk > threshold).
- Assumptions/dependencies: Lightweight Γk proxies (e.g., drift of logits on anchor probes) for on-device constraints.
- Model documentation and governance
- What: Include “Forgetting Profile Cards” in model cards: average Γk, spikes at distribution shifts, mitigation steps taken.
- Sectors: Policy, compliance, regulated industries.
- Tools/products/workflows: Audit-ready reports linking Γk to major updates and deployment decisions.
- Assumptions/dependencies: Versioned logs of Γk and training events; reproducibility.
Long-Term Applications
These applications require further research, scaling, or development to be production-ready.
- Forgetting-aware training objectives and regularizers
- What: Add Γk-based penalties or constraints to the loss to enforce k-step consistency (minimize D(q vs q*_k)) while optimizing task performance.
- Sectors: Cross-industry; safety-critical AI.
- Tools/products/workflows: Custom optimizers with dual variables (accuracy vs. Γk), layer-wise consistency penalties.
- Assumptions/dependencies: Efficient differentiable surrogates for Γk; stable estimators for longer horizons.
- Certified non-forgetful learners
- What: Algorithms with provable k-step consistency guarantees under bounded updates, used where regression of capabilities is unacceptable.
- Sectors: Healthcare diagnostics, aerospace, autonomous driving, industrial control.
- Tools/products/workflows: Training-time constraints, verification harnesses, deployment-time certificates.
- Assumptions/dependencies: Formal coherence of predictive mapping; verifiable bounds on update dynamics.
- Adaptive capacity allocation and memory systems
- What: Dynamic modules that allocate representational capacity to new data while protecting induced futures for prior competencies (e.g., routing, sparse experts, episodic memory).
- Sectors: Robotics, edge AI, foundation models.
- Tools/products/workflows: Controllers optimizing “capacity vs. Γk” trade-offs; retrieval-augmented policies guided by Γk.
- Assumptions/dependencies: Routing signals aligned with Γk; hardware support for dynamic sparsity.
- RL algorithms designed for non-stationarity via consistency control
- What: New off-policy/on-policy methods that jointly stabilize data distribution shifts and Γk (e.g., update gating, adaptive replay horizons, consistency-constrained policy updates).
- Sectors: Robotics, energy grids, supply chain, finance.
- Tools/products/workflows: “Consistency-constrained RL” libraries; multi-objective tuning (return, stability, Γk).
- Assumptions/dependencies: Reliable Γk in non-stationary loops; hybrid q_e choices that reflect task physics.
- Test-time adaptation with forgetting budgets
- What: On-the-fly adaptation mechanisms that enforce a per-session/per-slice Γk budget to prevent capability erosion during TTAs.
- Sectors: On-device inference, AR/VR, autonomous systems.
- Tools/products/workflows: Controllers that admit/deny updates based on projected Γk; anchor-probe sets for fast estimation.
- Assumptions/dependencies: Fast Γk proxies; robust anchor sets.
- Knowledge distillation that preserves induced futures
- What: Distillation objectives matching not just outputs but the teacher’s induced futures, improving robust transfer without losing capabilities.
- Sectors: Model compression, edge deployment.
- Tools/products/workflows: Sequence-level future matching, rollout-based teacher forcing with Γk constraints.
- Assumptions/dependencies: Tractable future approximations; scalable divergences.
- Standardized “Forgetting Stability” benchmarks and leaderboards
- What: Community benchmarks that report Γk across i.i.d., CL, RL, and generative tasks; new SOTA defined by accuracy × stability.
- Sectors: Academia, open-source ecosystems.
- Tools/products/workflows: Open datasets with scripted shifts; reference implementations of Γk.
- Assumptions/dependencies: Agreement on divergence choices and rollout protocols.
- Regulatory standards and safety cases for online learning
- What: Policies that require continuous monitoring of predictive self-consistency (Γk), thresholds for pause/rollback, and incident reporting.
- Sectors: Healthcare, finance, transportation, public-sector AI.
- Tools/products/workflows: Compliance toolkits; auditable Γk logs tied to deployment gates.
- Assumptions/dependencies: Regulator guidance; sector-specific risk thresholds.
- Interplay with data governance and machine unlearning
- What: Use Γk to validate that removing data or applying unlearning does not inadvertently erode unrelated competencies; or, conversely, to confirm targeted forgetting succeeded.
- Sectors: Privacy, legal compliance (GDPR/CCPA).
- Tools/products/workflows: “Selective retention checks” post-unlearning; impact radii via Γk.
- Assumptions/dependencies: Mapping between data segments and futures; reproducible rollouts.
- Neuro-symbolic and architecture co-design for stable futures
- What: Architectures that enforce predictive coherence (e.g., modular semantics with stateful inference-mode updates) to reduce destructive forgetting.
- Sectors: Safety-critical AI, enterprise applications.
- Tools/products/workflows: Component-level Γk budgets; symbolic constraints over induced futures.
- Assumptions/dependencies: Hybrid modeling stacks; interpretable module interfaces.
Notes on assumptions and dependencies (common to many applications)
- Coherent predictive mapping: The learner must induce a well-defined predictive distribution over futures; during transients (e.g., target-network resets), Γk is undefined and should be skipped or annotated.
- Induced futures approximation: In practice, use short horizons k, minibatch subsets, and task-appropriate divergences (KL for classification/regression, MMD/energy distances for generative modeling, policy/value divergences in RL).
- Computational overhead: Rollouts and divergences add cost; amortize by sampling, reduced frequency, or proxy metrics (e.g., logit drift on anchor probes).
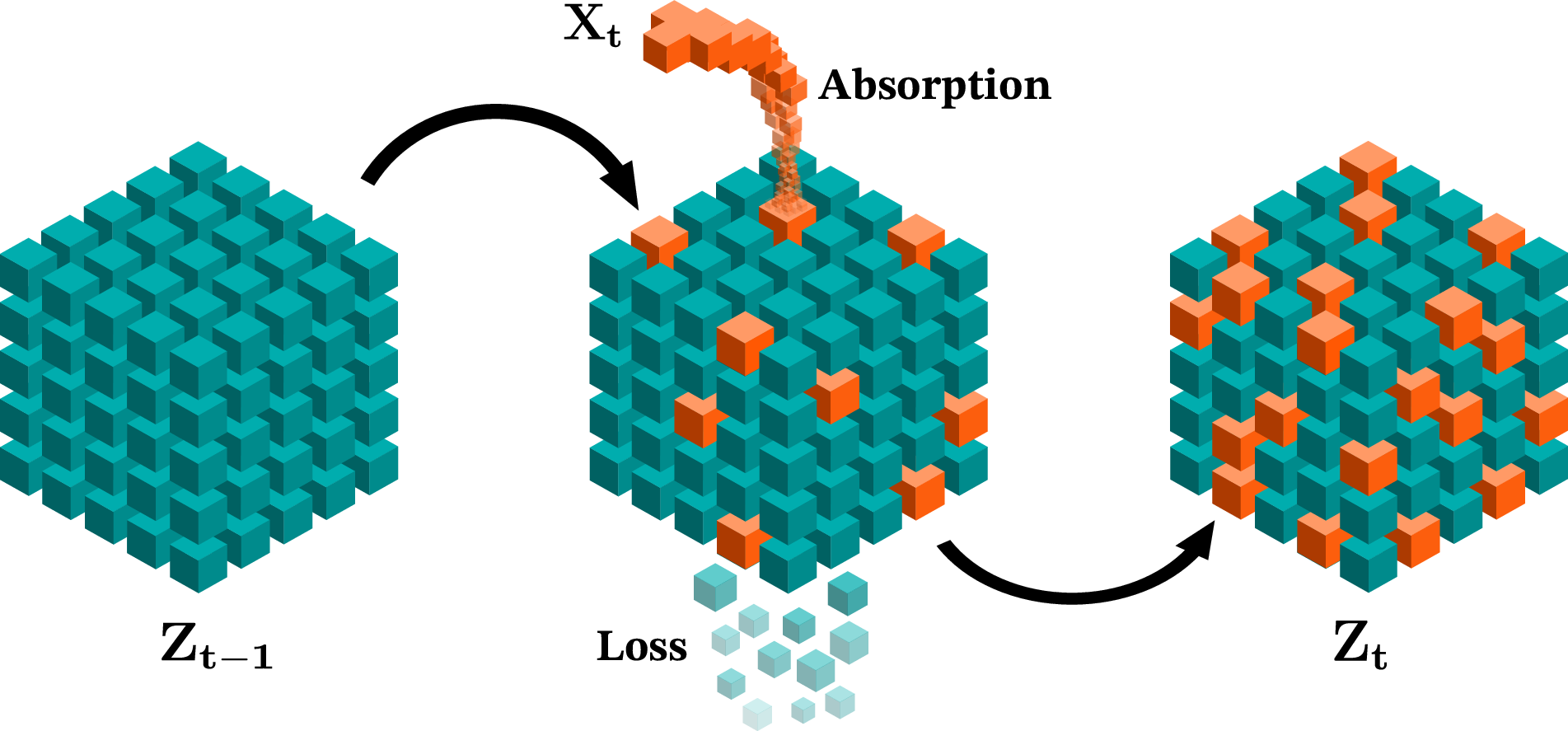
- Environment hybrid q_e: For RL/interactive tasks, define how environment components are borrowed during induced futures; validity depends on fidelity of this hybridization.
- Metric choice sensitivity: Γk magnitude depends on divergence choice and scaling; use within-task normalization and track trends/spikes rather than absolute values.
These applications leverage the paper’s central insight—forgetting as violations of predictive self-consistency—to make learning systems observable, tunable, and ultimately safer and more efficient across supervised, generative, and reinforcement learning settings.
Glossary
- agent–environment perspective: A framework in reinforcement learning that models interactions as between an agent and its environment. "The formalism draws inspiration from the agent-environment perspective from general RL"
- backward transfer: Improvement on earlier tasks caused by learning new tasks. "backward transfer, where new learning improves performance on past tasks"
- Borel σ-algebras: Collections of sets forming the standard measurable structure on topological spaces, used to define probability measures. "Borel σ-algebras of Polish spaces"
- cartpole environment: A classic control benchmark used to evaluate RL algorithms. "a DQN learner trained on the cartpole environment."
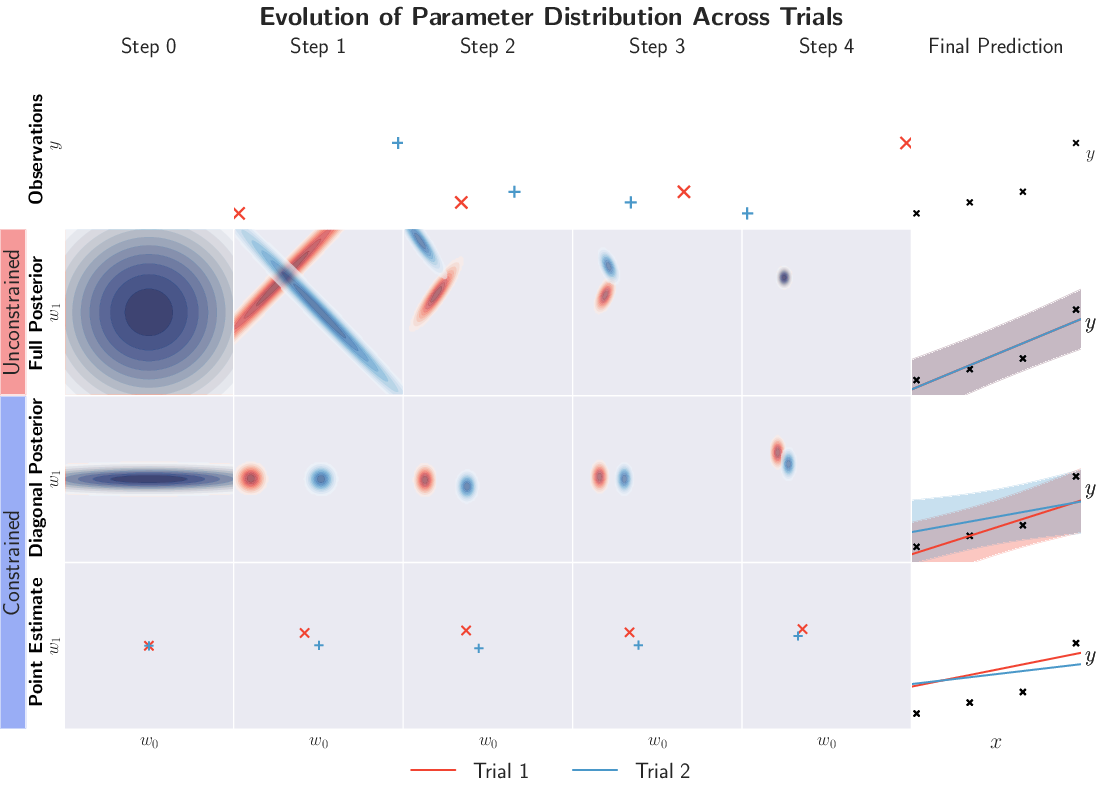
- class-incremental learning: A continual learning setting where new classes are introduced over time and the model must adapt without forgetting. "A class-incremental learning example using a single-layer neural network on a two-moons classification task."
- conditional probability kernels: Measurable mappings that assign conditional probability distributions given inputs. "conditional probability kernels and exist and are measurable."
- deep RL: Reinforcement learning methods that use deep neural networks for function approximation. "with deep RL being particularly susceptible to forgetting"
- distribution shift: Changes in the data-generating distribution over time that affect model performance. "Distribution shift and stochasticity strongly influence forgetting dynamics."
- DQN: Deep Q-Network, a value-based deep reinforcement learning algorithm. "a DQN learner trained on the cartpole environment."
- environment–learner interface: The formal pair of spaces describing observations and outputs exchanged at each step. "An environment-learner interface is a pair of measurable spaces."
- generative modelling: Learning to model or sample from the data distribution. "including regression, classification, generative modelling, and reinforcement learning."
- hybrid distribution: A constructed distribution for induced futures that uses the learner’s predictions as targets while borrowing environment components. "where is a hybrid distribution that treats the learner's predictions as targets while borrowing components from the environment as needed,"
- i.i.d.: Independent and identically distributed; a standard assumption for training data being drawn independently from the same distribution. "independent and identically distributed (i.i.d.) data"
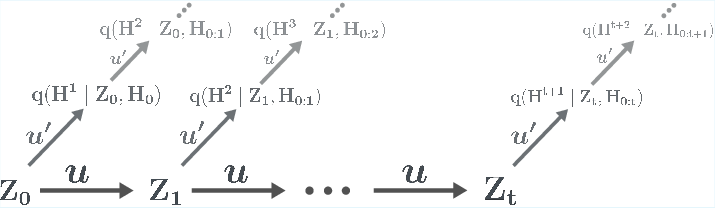
- induced future distribution: The learner’s predictive distribution over entire hypothetical future sequences given its current state. "The induced future distribution of the learner at state with realised history is the joint distribution"
- inference-mode update: A state update that evolves auxiliary components while keeping predictive parameters fixed. "an inference-mode state update function ;"
- interaction process: The stochastic process defined by the coupled evolution of environment observations, learner outputs, and learner state. "The (learning-mode) interaction process between an environment and a learner relative to an interface is the stochastic process over defined by:"
- k-step consistent: A property requiring that futures induced before updates are recoverable after k interactions via marginalisation over possible paths. "For , a learner is -step consistent if and only if"
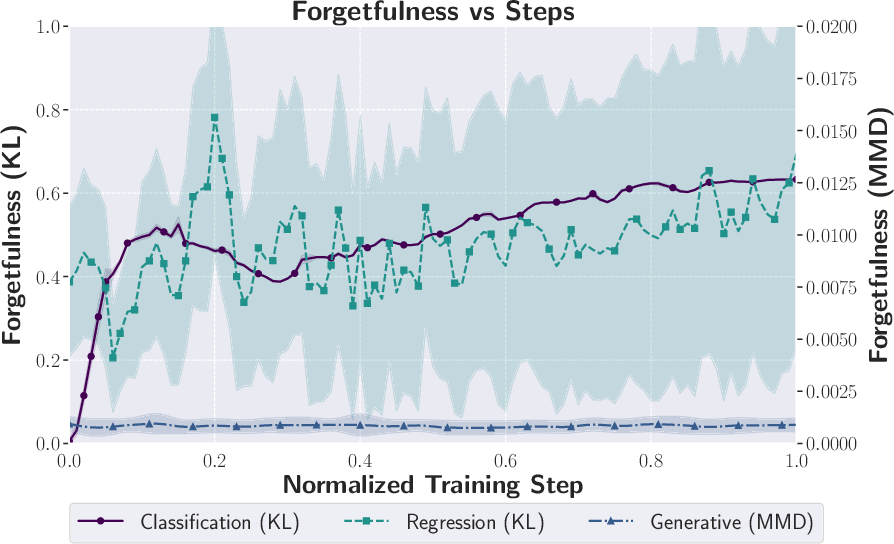
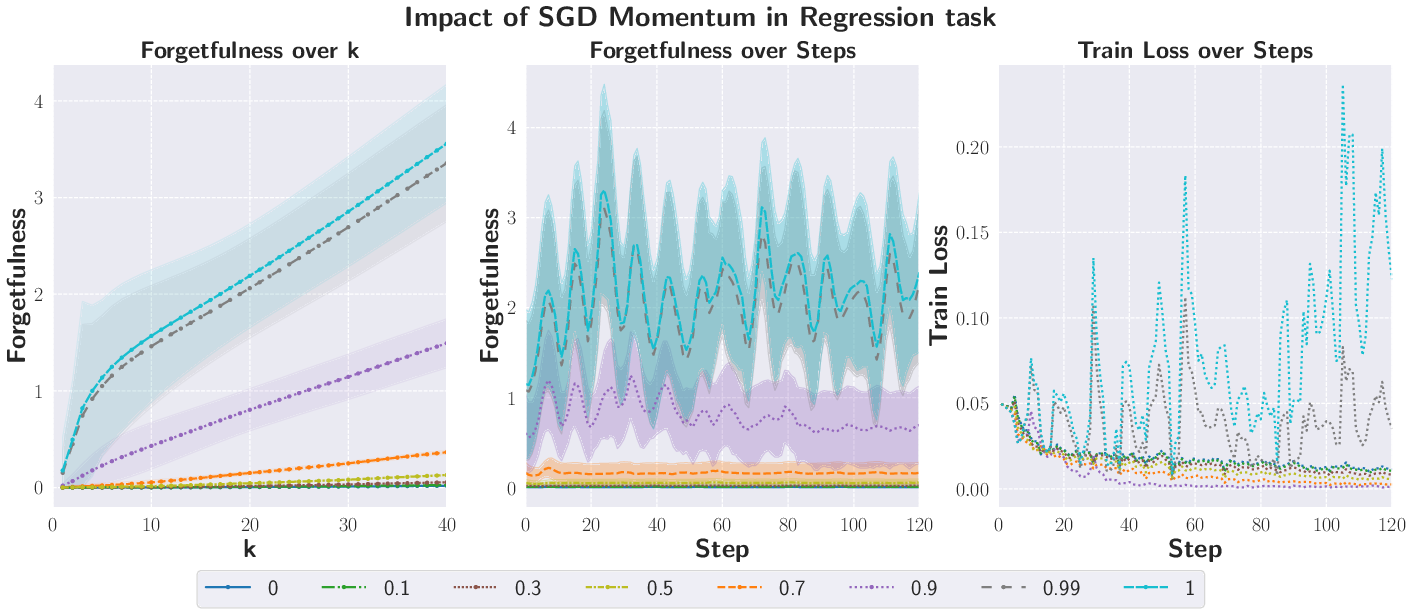
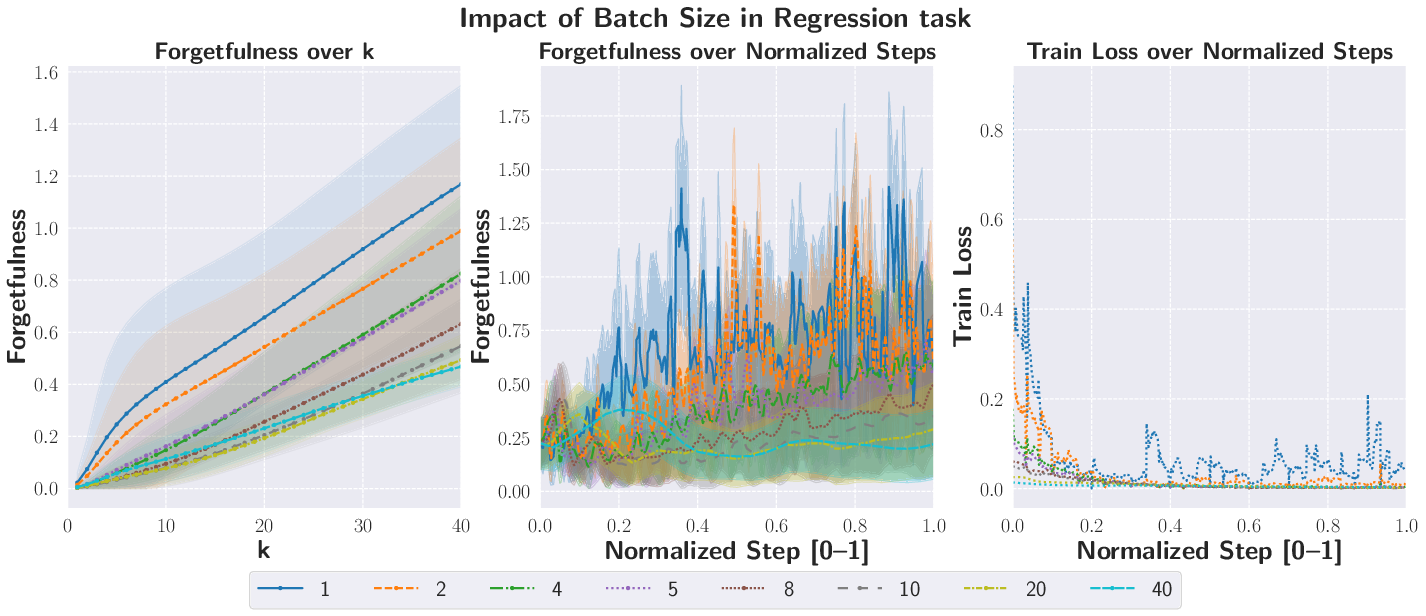
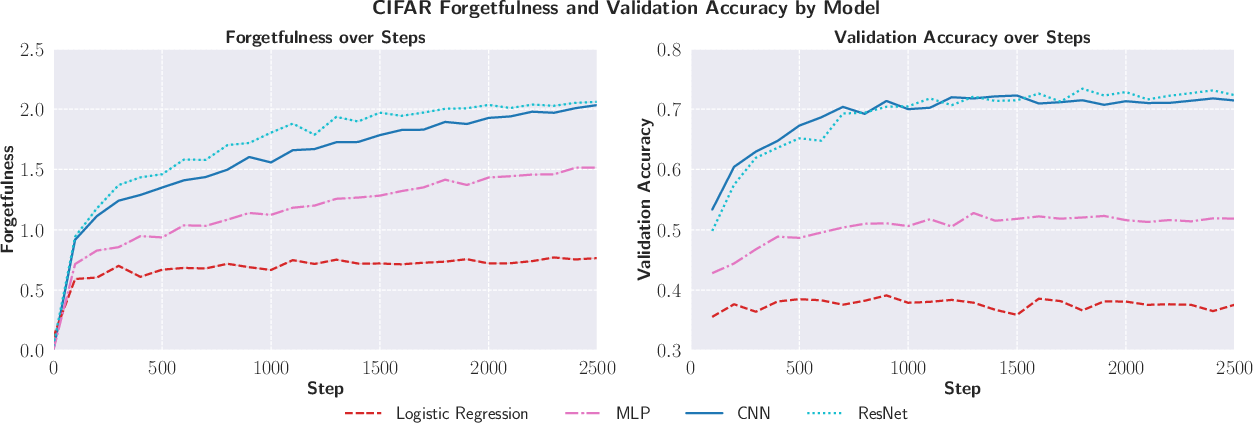
- KL divergence: A measure of difference between probability distributions used to quantify forgetfulness in classification and regression. "Regression and classification tasks use KL divergence, while the generative task uses the maximum mean discrepancy (MMD)."
- learning-mode update: A state update during training that changes predictive parameters and auxiliary structures. "a learning-mode state update function ;"
- maximum mean discrepancy (MMD): A kernel-based divergence between distributions used to measure forgetfulness in generative tasks. "maximum mean discrepancy (MMD)."
- non-stationarity: The property of a process whose distribution changes over time, common in RL training dynamics. "RL, however, remains non-stationary throughout the training process."
- policy churn: Rapid, widespread changes in the greedy policy after few updates, indicating instability. "the phenomenon of policy churn identified by \citep{schaul2022phenomenon} in which the greedy policy of a value-based learner changes in a large portion of the input space after just a few updates."
- policy gradient methods: RL algorithms that optimise policies directly via gradient ascent on expected returns. "Policy gradient methods are also prone to overwriting earlier strategies during continual adaptation"
- Polish spaces: Complete separable metric spaces foundational in measure-theoretic probability. "Polish spaces"
- predictive-Bayesian framework: A Bayesian viewpoint focusing on predictive distributions rather than latent parameters. "conceptually inspired by the predictive Bayesian framework"
- predictive distribution: The learner’s probability distribution over future observations or experiences given its current state. "self-consistency in a learner's predictive distribution over future experiences"
- Propensity to Forget: A divergence-based measure quantifying how much a learner violates predictive consistency over k steps. "The -step propensity to forget incurred at time is measured as the divergence"
- Q-value: The expected cumulative reward of taking an action in a state and following a policy thereafter. "Q-value evaluation across ten seeds"
- replay buffers: Memory structures that store past experiences to stabilise training via replay. "Replay buffers are widely used to mitigate these effects by reintroducing past experiences during training"
- self-consistency: The requirement that sequential predictions remain compatible with prior predictive beliefs. "violation of self-consistency in a learner's predictive distribution"
- standard Borel: Measurable spaces arising from Borel σ-algebras on Polish spaces, ensuring technical measurability properties. "standard Borel (Borel σ-algebras of Polish spaces)"
- stationarity: The property that a process’s distribution does not change over time. "In i.i.d.\ environments, the interaction process is stationary"
- stochastic process: A collection of random variables indexed by time describing evolving random phenomena. "as the learner interacts with the environment, the sequence forms a stochastic process."
- TD loss: Temporal-Difference loss used in value-based RL to train value estimators. "We show TD loss and Q-value evaluation across ten seeds"
- target-network lag: A stabilisation technique in value-based RL where a slowly updated target network creates a lag between networks. "such as buffer reinitialisation, target-network lag, or policy resets"
- value-based methods: RL algorithms that learn value functions to derive policies, such as Q-learning. "Value-based methods with function approximation often lose performance on earlier estimates"
Collections
Sign up for free to add this paper to one or more collections.