Twist and higher modes of a complex scalar field at the threshold of collapse (2511.04649v1)

Abstract: We investigate the threshold of collapse of a massless complex scalar field in axisymmetric spacetimes under the ansatz of Choptuik et al. 2004, in which a symmetry depending on the azimuthal parameter $m$ is imposed on the scalar field. This allows for both non-vanishing twist and angular momentum. We extend earlier work to include higher angular modes. Using the pseudospectral code bamps with a new adapted symmetry reduction method, which we call $m$-cartoon, and a generalized twist-compatible apparent horizon finder, we evolve near-critical initial data to the verge of black hole formation for the lowest nontrivial modes, $m=1$ and $m=2$. For $m=1$ we recover discrete self-similarity with echoing period $\Delta\simeq0.42$ and power-law scaling with exponent $\gamma\simeq0.11$, consistent with earlier work. For $m=2$ we find that universality is maintained within this nonzero fixed-$m$ symmetry class but with smaller period and critical exponents, $\Delta\simeq0.09$ and $\gamma\simeq0.035$, establishing an explicit dependence of the critical solution on the angular mode. Analysis of the relation between the angular momentum and the mass of apparent horizons at the instant of formation, $J_{\mathrm{AH}}{-}M_{\mathrm{AH}}$, shows that the effect of angular momentum is minimal at the threshold, with $\chi_{\mathrm{AH}}=J_{\mathrm{AH}}/M_{\mathrm{AH}}^2\to0$, and, therefore, excludes extremal black holes for the families under consideration. Our results demonstrate that while universality and DSS hold within each $m$-sector, the critical universal values vary with $m$, and neither extremality nor bifurcation occur in the complex scalar field model within the families considered here.

• The paper introduces a novel approach to explore twist and higher angular modes, revealing mode-specific discrete self-similarity and scaling exponents.
• High-resolution pseudospectral simulations using the m-cartoon method demonstrate universal critical phenomena and precise horizon properties near collapse.
• Results show angular momentum suppression at the threshold, ruling out extremal or bifurcate horizons across azimuthal quantum numbers m=1 and m=2.

Critical Collapse of Complex Scalar Fields with Twist and Higher Angular Modes

This essay examines the findings and implications of "Twist and higher modes of a complex scalar field at the threshold of collapse" (2511.04649). The work extends axisymmetric critical collapse studies for massless complex scalar fields by incorporating angular momentum (twist) and probing higher azimuthal quantum numbers ($m=1$, $m=2$). Using high-resolution pseudospectral simulations (bamps code) and novel methods for symmetry reduction (m-cartoon) and horizon classification, the authors reveal the mode-dependent nature of universality and self-similarity at the collapse threshold. The absence of extremality and bifurcation phenomena is quantitatively established, advancing both theoretical understanding and computational methodology in critical phenomena.

Formulation and Numerical Approach

The system is a massless complex scalar field in $3+1$ dimensional axisymmetry, evolving under an azimuthal phase factor $e^{im\phi}$ (Choptuik-type ansatz), yielding non-trivial twist and angular momentum. The coupled Einstein-Klein-Gordon system is discretized using the generalized harmonic gauge. Key aspects of the computational framework:

• Symmetry Reduction: The m-cartoon method generalizes the traditional cartoon technique, enabling efficient $2+1$ evolution while consistently accounting for $m\neq0$ azimuthal dependence in both field derivatives and metric contributions.
• Initial Data: Smooth, regular axisymmetric pulses are constructed, parameterized per family to control $m$ and field profiles, ensuring compatibility with the spectral code's requirements.
• Apparent Horizon Finding: A generalized horizon finder accommodates twist and extracts horizon mass and angular momentum quasilocally at high precision ($\sim 10^{-7}$ constraint violations).
• Adaptive Mesh Refinement: hp-refinement dynamically resolves increasingly smaller scales near criticality, backed by polynomial and grid refinement, enabling detailed phase-space explorations.

Universality and Discrete Self-Similarity Across Modes

$m=1$ Families

Simulations for $m=1$ recover the expected features of type II critical phenomena: discrete self-similarity (DSS) with echoing period $\Delta \simeq 0.42$, and power-law scaling for curvature invariants and black hole mass with exponent $\gamma \simeq 0.11$.

• Scaled Field Derivatives: Central values of $(\tau_*-\tau)\,\partial_x\Phi/\rho_c$ show oscillatory DSS behavior, with period $\Delta$ consistent across families despite differences in field amplitudes.

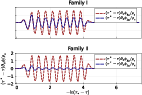
  Figure 1: Scaled derivatives of the scalar field at the center for the best tuned subcritical evolutions, showing DSS oscillations with universal period $\Delta$ across families.

• Curvature Invariants: The Kretschmann scalar measured in DSS-adapted similarity coordinates displays periodic echoes, confirming universality at the metric level.

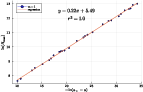
  Figure 2: Log-log plot of the maximum Ricci scalar $R_{\text{max}$ displaying power-law scaling with slope $2\gamma$, validating universality of critical exponents for $m=1$.

• Apparent Horizon Properties: The mass $M_{\mathrm{AH}$ and angular momentum $J_{\mathrm{AH}$ at formation both scale, with $J_{\mathrm{AH}/M_{\mathrm{AH}^2 \to 0$ as threshold is approached. No evidence for extremal or bifurcate horizon formation.

  Figure 3: Angular momentum versus mass at horizon formation, showing the rapid decrease of dimensionless spin $\chi_{\mathrm{AH}$ toward zero near criticality.

$m=2$ Families

With $m=2$, field access at the origin requires second derivatives, yielding:

• Distinct Critical Parameters: DSS echoing period $\Delta \simeq 0.09$ and scaling exponent $\gamma \simeq 0.035$—both noticeably smaller than for $m=1$—demonstrating explicit dependence on angular mode.

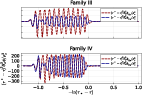
  Figure 4: Scaled second derivatives of the scalar field at the center for $m=2$ families, presenting DSS echoes with shorter period.

• Curvature and Scaling: Universal scaling for curvature invariants and black hole mass persists within each fixed-$m$ sector, with phase-space scaling laws robust to variation in initial data.

  Figure 5: Supercritical scaling of $M_{\mathrm{AH}$ for $m=2$ families, fit with exponent matching subcritical curvature scaling.

• Angular Momentum: As with $m=1$, $J_{\mathrm{AH}$ decreases rapidly, precluding extremality at threshold for $m=2$ data.

Absence of Extremality and Bifurcation

No simulation across any family or mode produced evidence of threshold solutions with near-extremal dimensionless spin, nor did horizon bifurcation or multi-centered collapse appear. Analysis in the Lyapunov framework shows negative subdominant exponents ($\lambda_1<0$), ensuring angular momentum decays faster than mass near criticality. This rules out the formation of extremal Kerr-like black holes at threshold within the examined symmetry classes.

Gravitational Wave Content and Threshold Competition

The universality of the critical solution is maintained despite significant asphericity and gravitational wave contributions in the strong field region.

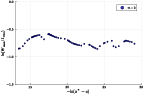
Figure 6: Log-log plot of the ratio of maxima of Weyl and Kretschmann invariants, showing constancy near threshold and implying gravitational wave content remains a major component without dominating threshold dynamics.

Unlike previous twist-free studies showing bifurcation and threshold competition between matter and vacuum channels, the m-twisting scenario yields single-center collapse and consistent critical scaling. Detailed vacuum analysis confirms that axisymmetric, rotating black hole threshold solutions do not exist from regular initial data in vacuum, excluding gravitational-wave-only competitors for threshold angular momentum in axisymmetry.

Implications and Future Directions

This work establishes that critical universality and self-similarity persist with twist and higher angular modes, but critical exponents and echoing periods are strictly mode-dependent. The absence of extremality at threshold has implications for both the scope of critical phenomena and conjectures relating charge and spin analogs in collapse scenarios. Technically, the m-cartoon and refined horizon analysis provide robust tools for future studies, including potential transitions to Type I collapse, inclusion of scalar field mass, and exploration of more complex initial data to seek extremal thresholds or new symmetry-breaking phenomena.

Further investigation into vacuum axisymmetric collapse with twist, as well as higher-dimensional and non-axisymmetric scenarios, is required to fully map the landscape of critical phenomena and threshold competition in general relativity.

Conclusion

The incorporation of twist and higher angular modes in axisymmetric complex scalar field collapse extends the understanding of critical phenomena beyond spherical and twist-free frameworks. Critical solutions remain universal and self-similar within each fixed-$m$ symmetry sector, but exhibit explicit mode dependence in scaling exponents and DSS periods. Angular momentum is systematically suppressed at the threshold; no evidence for extremal or bifurcate critical behavior is observed within the broad range of families probed. These findings reinforce the robustness of critical phenomena in gravitational collapse, delineate the boundaries where threshold competition may arise, and provide computational and theoretical foundation for future explorations in high-dimensional and more generic settings.