Cross-Modal Alignment via Variational Copula Modelling (2511.03196v1)

Abstract: Various data modalities are common in real-world applications (e.g., electronic health records, medical images and clinical notes in healthcare). It is essential to develop multimodal learning methods to aggregate various information from multiple modalities. The main challenge is how to appropriately align and fuse the representations of different modalities into a joint distribution. Existing methods mainly rely on concatenation or the Kronecker product, oversimplifying the interaction structure between modalities and indicating a need to model more complex interactions. Additionally, the joint distribution of latent representations with higher-order interactions is underexplored. Copula is a powerful statistical structure for modelling the interactions among variables, as it naturally bridges the joint distribution and marginal distributions of multiple variables. We propose a novel copula-driven multimodal learning framework, which focuses on learning the joint distribution of various modalities to capture the complex interactions among them. The key idea is to interpret the copula model as a tool to align the marginal distributions of the modalities efficiently. By assuming a Gaussian mixture distribution for each modality and a copula model on the joint distribution, our model can generate accurate representations for missing modalities. Extensive experiments on public MIMIC datasets demonstrate the superior performance of our model over other competitors. The code is available at https://github.com/HKU-MedAI/CMCM.

• The paper introduces CM², a copula-driven multimodal framework that models joint distributions to capture higher-order interactions across diverse modalities.
• It employs Gaussian mixture modeling for each modality’s marginal distribution and uses variational inference to robustly impute missing data.
• Empirical results on MIMIC datasets demonstrate up to a 3.2% improvement in AUPR over baselines, validating the effectiveness of the copula approach.

Cross-Modal Alignment via Variational Copula Modelling

Introduction and Motivation

The paper presents CM$^{2}$, a copula-driven multimodal learning framework designed to address the limitations of existing fusion strategies in multimodal representation learning. Traditional approaches, such as concatenation or Kronecker product, fail to capture higher-order interactions between heterogeneous modalities (e.g., EHRs, medical images, clinical notes), resulting in suboptimal joint representations. CM$^{2}$ leverages copula theory to model the joint distribution of modality-specific embeddings, enabling more expressive alignment and fusion. The framework is particularly suited for scenarios with missing modalities, as it can impute missing representations via learned marginal distributions.

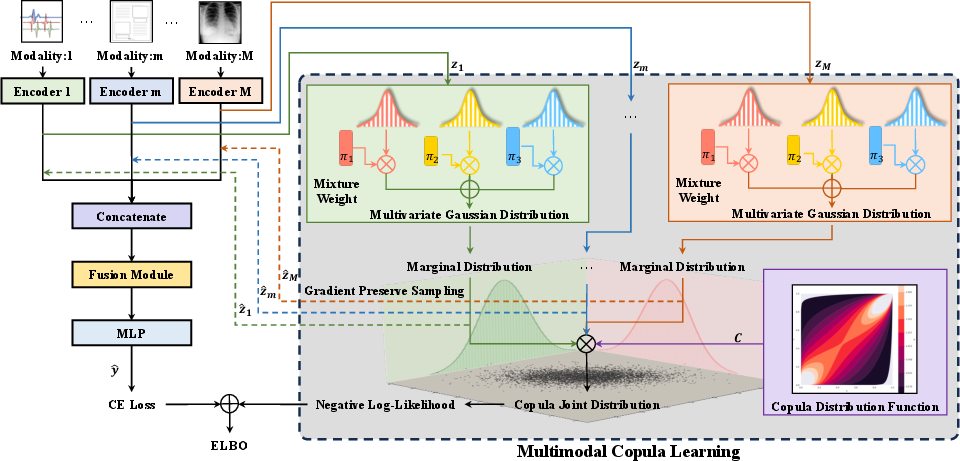
Figure 1: Overview of the CM$^{2}$ framework, illustrating modality-specific embedding extraction, GMM-based marginal modeling, copula-based joint estimation, and fusion/classification pipeline.

Methodological Framework

Copula-Based Joint Distribution Modeling

CM$^{2}$ interprets copula models as distribution alignment tools, grounded in Sklar's theorem, which guarantees the existence and uniqueness of a copula linking marginal and joint distributions for continuous variables. Each modality's embedding is modeled as a Gaussian mixture, providing flexibility for high-dimensional, non-Gaussian data. The joint distribution is then constructed using a multivariate copula, with the copula parameter $\alpha$ (or $\rho$ for Gaussian copulas) learned via stochastic variational inference.

Marginal Modeling and Imputation

For each modality $m$, the marginal density is parameterized as:

$$f_m(\mathbf{z}_m) = \sum_{k=1}^K \pi_{mk} \mathcal{N}(\mu_{mk}, \Sigma_{mk})$$

where mixture weights $\pi_{mk}$ are predicted by an MLP with softmax output, and $\mu_{mk}, \Sigma_{mk}$ are trainable via backpropagation. Missing modalities are imputed by sampling from the learned GMM, ensuring that the generated embeddings reflect both marginal and joint dependencies.

Variational Inference and Optimization

The evidence lower bound (ELBO) objective combines the copula log-likelihood and task-specific loss (e.g., cross-entropy for classification):

$$\text{ELBO} = -\lambda_{\text{cop}} \sum_{i=1}^n \left[ \log c(Q_1(\mathbf{z}_1^{(i)}), \ldots, Q_M(\mathbf{z}_M^{(i)})) - \sum_{m=1}^M \log f_m(\mathbf{z}_m^{(i)}) \right] + \mathcal{L}_{\text{obj}}$$

Gradients are propagated to all model parameters, including copula parameters, GMM parameters, and fusion/classification layers.

Copula Families and Interaction Modeling

The framework supports various copula families (Gumbel, Gaussian, Frank), each capturing different dependency structures. Empirical analysis demonstrates that the choice of copula affects the model's ability to capture tail dependencies and symmetry in modality interactions.

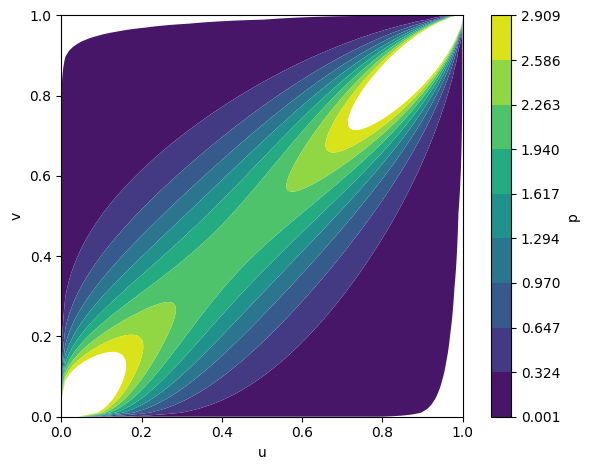
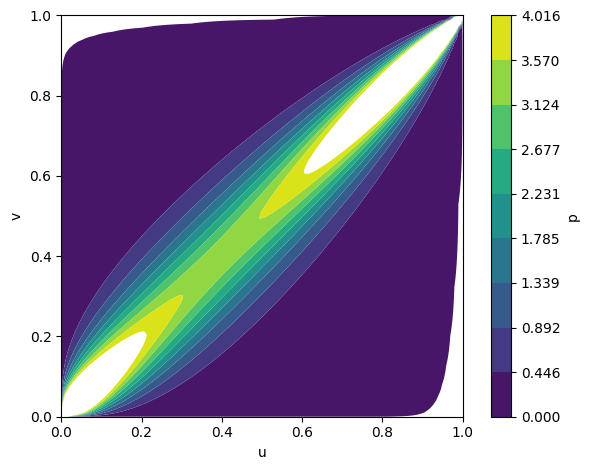
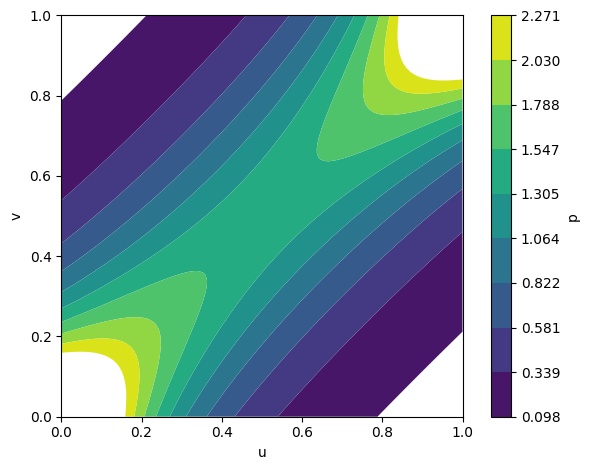
Figure 2: Fitted copula densities for Gumbel, Gaussian, and Frank families, illustrating distinct inter-modality dependency structures.

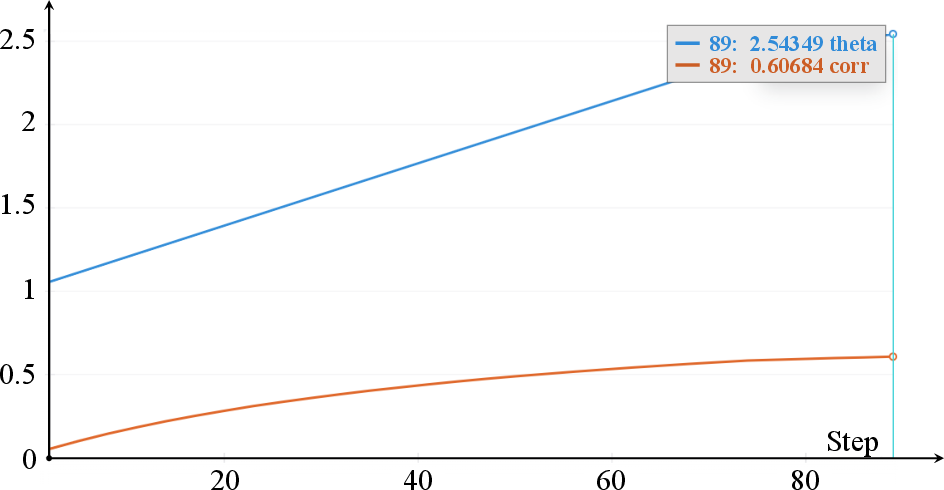
Figure 3: Evolution of the Gumbel copula parameter $\alpha$ and the induced correlation $\text{Corr} = \frac{\alpha-1}{\alpha}$ over training epochs.

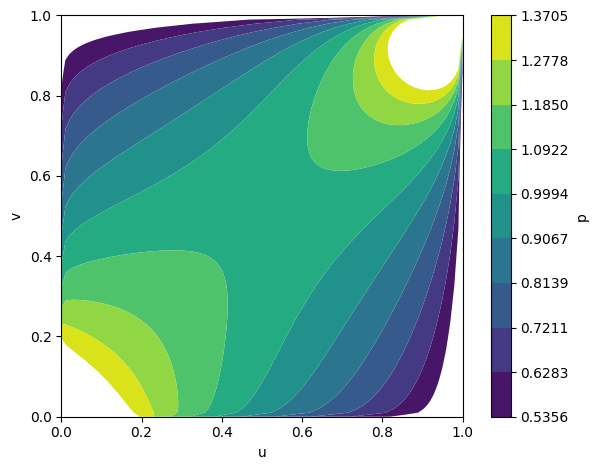
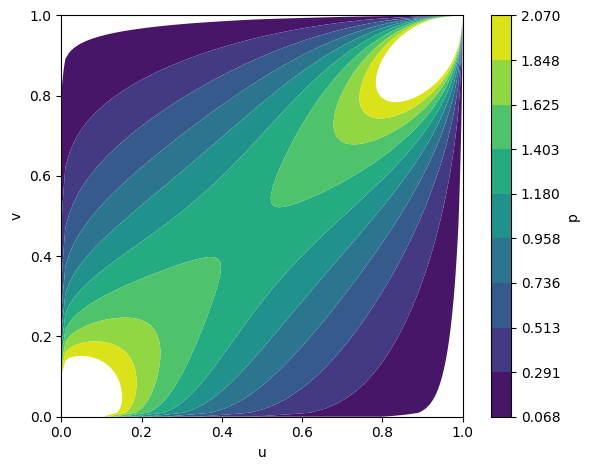
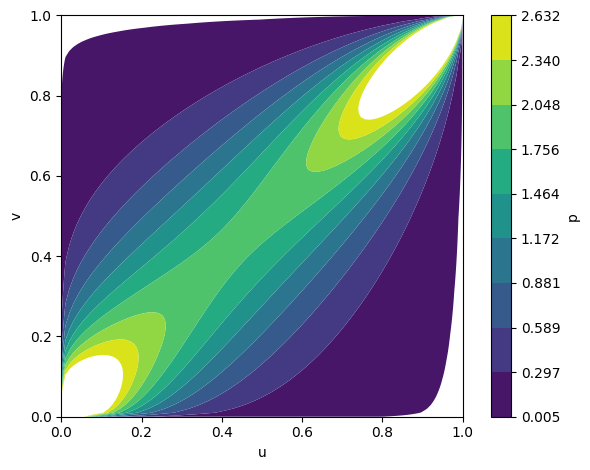
Figure 4: Temporal evolution of Gumbel copula densities at epochs 5, 50, and 100, showing progressive learning of positive dependence.

Empirical Evaluation

Datasets and Experimental Setup

Experiments are conducted on MIMIC-III, MIMIC-IV, and MIMIC-CXR datasets, encompassing EHR time series, chest X-ray images, clinical notes, and radiology reports. Both fully matched and partially matched (missing modality) scenarios are evaluated. Backbone encoders include ResNet34 for images, LSTM for time series, and TinyBERT for text.

Quantitative Results

CM$^{2}$ consistently outperforms competitive baselines (MMTM, DAFT, Unified, MedFuse, DrFuse) in AUROC and AUPR across both IHM and READM tasks. Notably, CM$^{2}$ achieves up to 3.2% improvement in AUPR over the best baseline on MIMIC-IV. The framework demonstrates robustness to missing modalities, with superior performance in partially matched settings due to effective imputation and joint modeling.

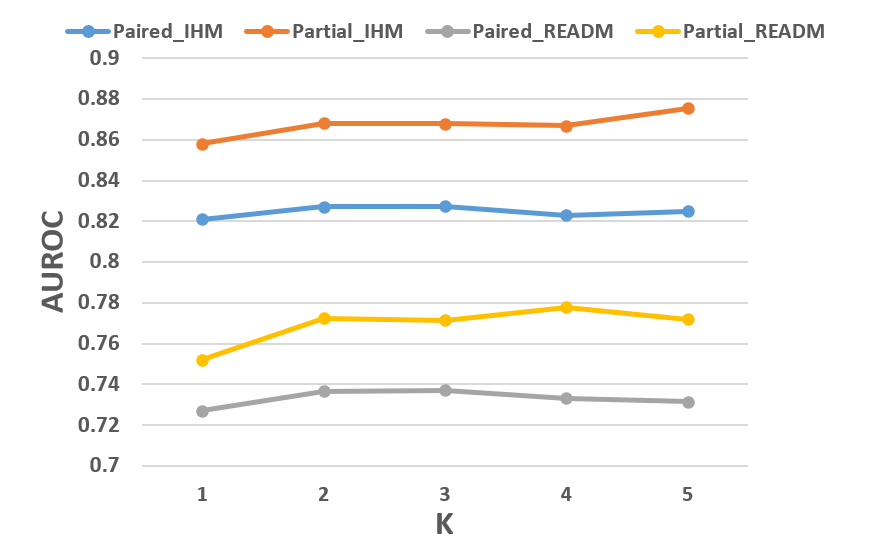
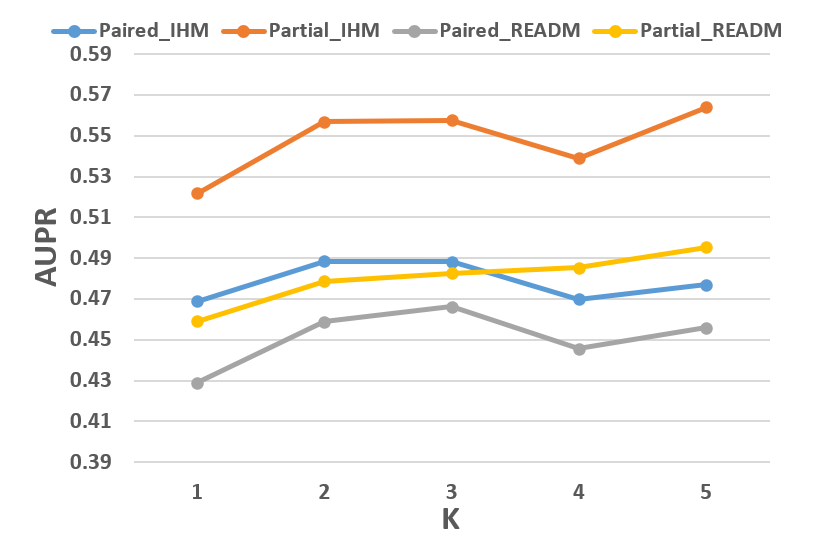
Figure 5: AUROC and AUPR results of CM$^{2}$ on MIMIC-IV, highlighting performance across different numbers of GMM mixtures.

Ablation and Sensitivity Analyses

• Alignment Loss: Copula-based alignment outperforms cosine similarity and KL divergence.
• Module Contribution: Removal of copula alignment or fusion module leads to significant performance degradation, underscoring their necessity.
• Copula Family Choice: Performance is robust across copula families, but optimal choice is task-dependent.
• Scalability: Stochastic variational inference enables training on large-scale datasets with moderate computational overhead (single RTX-3090 GPU, batch size 16–32).

Theoretical and Practical Implications

The use of copula modeling in multimodal learning provides a principled approach to joint distribution estimation, with theoretical guarantees from Sklar's theorem. The framework is extensible to additional modalities and can be adapted for other tasks requiring distribution alignment, such as domain adaptation and multi-view learning. The probabilistic imputation mechanism is particularly valuable in clinical and real-world settings with incomplete data.

Limitations and Future Directions

The non-convexity of the joint log-likelihood with respect to copula parameters may hinder optimization; future work could explore alternative algorithms (e.g., partial likelihood) for improved convergence. Extension to other domains and modalities, as well as integration with transformer-based fusion architectures, are promising avenues.

Conclusion

CM$^{2}$ introduces copula-based joint modeling to multimodal representation learning, enabling expressive alignment and robust handling of missing modalities. Empirical results validate its superiority over existing methods, and ablation studies confirm the critical role of copula alignment. The framework is theoretically grounded, practically scalable, and extensible to broader multimodal and distribution alignment tasks in machine learning.