Curvature of high-dimensional data (2511.02873v1)
Abstract: We consider the problem of estimating curvature where the data can be viewed as a noisy sample from an underlying manifold. For manifolds of dimension greater than one there are multiple definitions of local curvature, each suggesting a different estimation process for a given data set. Recently, there has been progress in proving that estimates of ``local point cloud curvature" converge to the related smooth notion of local curvature as the density of the point cloud approaches infinity. Herein we investigate practical limitations of such convergence theorems and discuss the significant impact of bias in such estimates as reported in recent literature. We provide theoretical arguments for the fact that bias increases drastically in higher dimensions, so much so that in high dimensions, the probability that a naive curvature estimate lies in a small interval near the true curvature could be near zero. We present a probabilistic framework that enables the construction of more accurate estimators of curvature for arbitrary noise models. The efficacy of our technique is supported with experiments on spheres of dimension as large as twelve.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Curvature of High-Dimensional Data — Explained Simply
What is this paper about?
Imagine you have a huge pile of data points—like pixels in images, or numbers that describe words. The “manifold hypothesis” says that even though the data lives in a space with many numbers (many dimensions), the points actually sit near a smoother, lower-dimensional shape (a manifold), kind of like how a thin sheet curves through 3D space.
This paper studies how to measure how “curvy” that hidden shape is, using the data points. It shows that common ways of measuring curvature can be very misleading, especially when the data has many dimensions or is noisy. Then it introduces a new, probability-based method to get more accurate curvature estimates.
What questions are the authors trying to answer?
The paper focuses on three simple questions:
- How can we define and measure curvature for real, noisy data?
- Why do popular curvature measurements become biased (systematically wrong) in high dimensions?
- Can we correct this bias and recover the true curvature reliably?
How do they approach the problem?
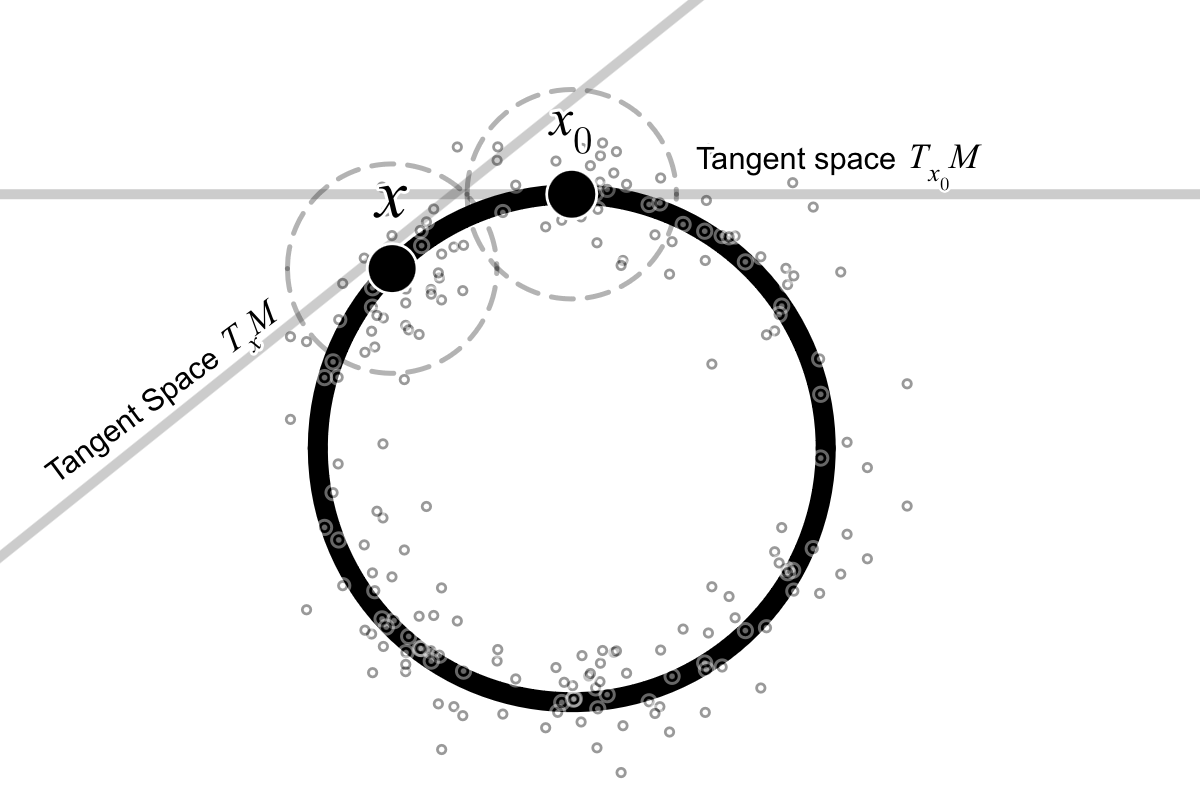
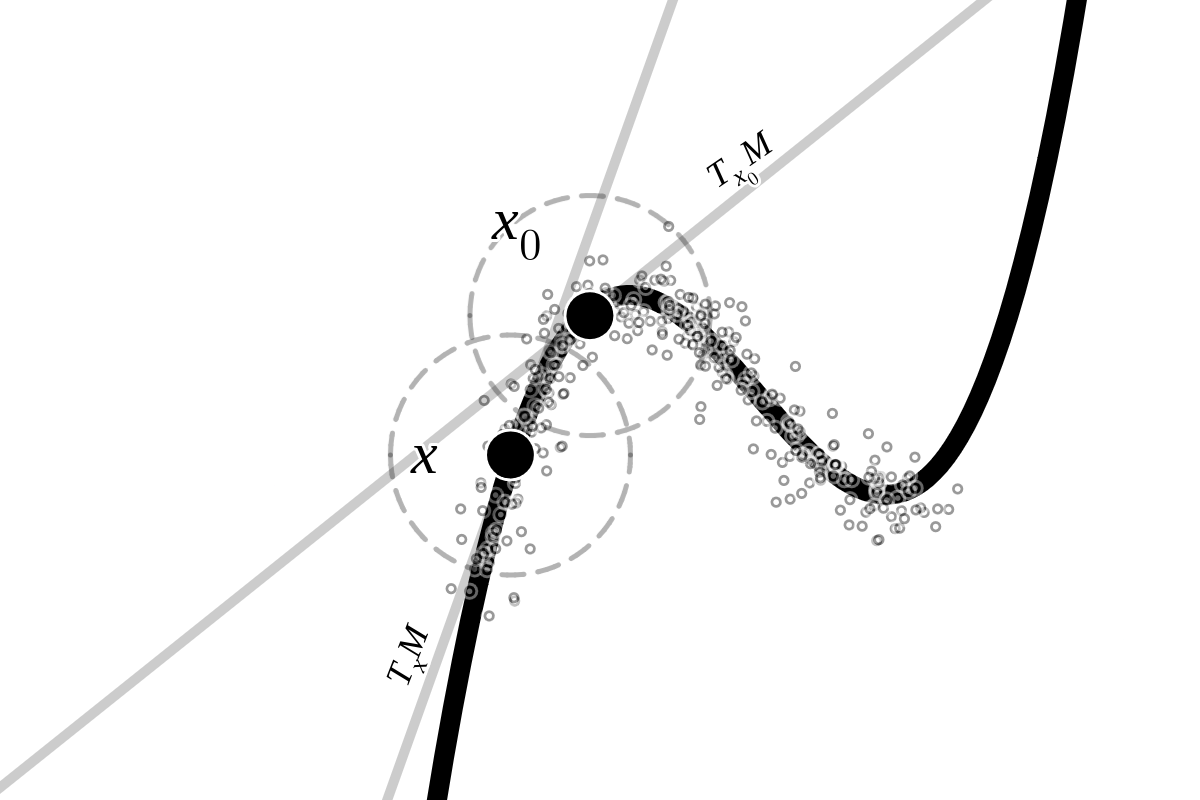
Think of curvature as “how quickly the direction of a tangent plane changes as you move along a surface.”
- A tangent plane is like a flat sheet that just touches a curved surface at a point (like placing a flat card on a ball).
- If the sheet’s direction changes a lot as you move, the surface has high curvature. If it barely changes, the curvature is low.
The authors use a curvature idea they call “absolute variation curvature.” In simple terms, at a point on the surface, they look around in all directions and average how much the tangent planes change.
But in real data, the tangent planes aren’t exact: we estimate them from nearby points, and those points are noisy. So the estimate depends on random noise. The authors treat the estimated curvature as a random variable and do three key things:
- They model the noise in the estimated tangent directions using a distribution for directions on a sphere called the von Mises–Fisher (vMF) distribution. You can think of vMF as “randomly pointing near a preferred direction,” with a knob (called the concentration parameter) that controls how tightly clustered it is.
- They compute how this directional noise “pushes forward” into noise in the angle between tangent planes, and then into noise in the curvature estimate. “Pushforward” here means: if your input is noisy, what is the resulting distribution of your computed output?
- Using that distribution, they can “decode” the true curvature by fitting the model to the observed noisy curvature values and choosing the true curvature that makes these observations most likely (this is a maximum likelihood estimate).
In practice, the noise may not be exactly vMF. To handle that, they show you can use mixtures of vMF distributions (like blending multiple bell-shaped patterns for directions) to approximate any reasonable noise.
What did they find, and why does it matter?
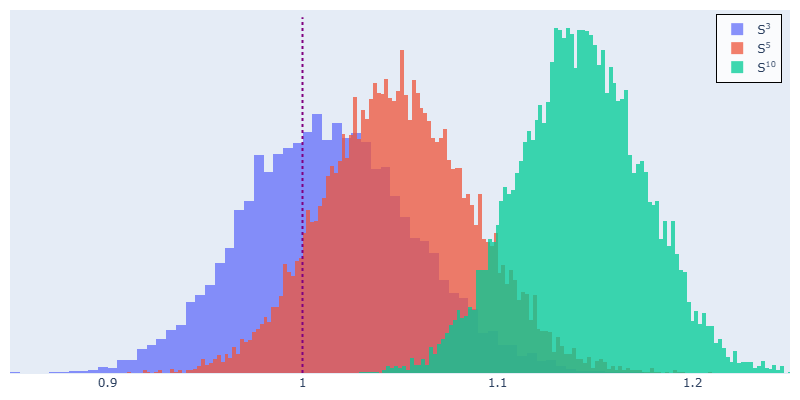
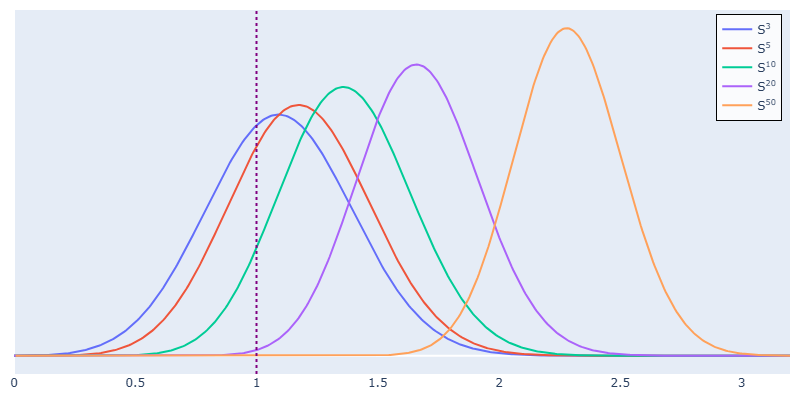
- Naive curvature estimates are biased, and the bias gets worse in higher dimensions and with more noise. In very high dimensions, the chance that your naive curvature falls near the true value can be almost zero.
- They prove, and then show with experiments, exactly how the noise in tangent directions produces biased angle and curvature estimates.
- They provide a probabilistic framework that gives a closed-form (explicit) formula for the distribution of the noisy curvature estimate (for the vMF noise model). This lets you correct the bias and recover the true curvature reliably from data.
- In experiments on spheres—surfaces where the true curvature is known—they test dimensions up to 12 and show their method matches the true curvature much better than the naive approach.
This matters because curvature is a key part of “data geometry.” It helps us understand the shape of complex datasets, find patterns, and build better tools for data analysis and machine learning. If our curvature estimates are biased, we may misunderstand the data’s structure.
What is the bigger impact?
- Better geometry-aware data analysis: The method helps researchers accurately measure geometric features of data (like curvature) even when the data is high-dimensional and noisy.
- Robustness in practice: Existing methods can theoretically work if you had infinite, perfectly clean data. This paper tackles the real world—finite, noisy samples—and provides a fix.
- Generalization: Although they present detailed results for shapes embedded with one extra dimension (codimension one) and for spheres, the idea extends. They show how to handle more general noise by mixing vMF distributions, and they discuss extensions toward more complex shapes and higher codimensions.
- Future directions: The same probabilistic decoding idea could be applied to other curvature types (like mean curvature, Ricci curvature, or quantities from the second fundamental form). That opens doors in image analysis, text embeddings, biomedical data, and any domain where high-dimensional geometry matters.
A simple summary
- You try to measure how “curvy” a hidden shape is from noisy data.
- Common methods look at changes in tangent planes but get biased, especially in high dimensions.
- The authors model the noise mathematically, compute how it affects angles and curvature, and then work backward to estimate the true curvature.
- Their method reduces bias and works well in experiments, even in high dimensions.
In short: the paper shows why naive curvature measurements fail for high-dimensional, noisy data—and how to fix them using probability.
Knowledge Gaps
Below is a single, consolidated list of concrete knowledge gaps, limitations, and open questions that remain unresolved in the paper. Each item highlights an actionable direction for future research.
- Codimension > 1 extension is only suggested, not developed: no explicit pushforward distributions on the Grassmannian/Stiefel manifolds, no choice/analysis of appropriate directional distributions (e.g., matrix vMF/Bingham), and no implementation details for multi-normal-vector noise.
- Base-point tangent uncertainty is ignored in theory: the analysis conditions on a fixed tangent at the base point x, while in practice both T_xM and T_yM are estimated with noise; a joint model for the two noisy tangents and its impact on bias/variance is missing.
- Mapping from ambient point noise and sampling density to vMF parameters is not derived: there is no theoretical link from Gaussian (or other) ambient noise, neighborhood size, and sample size to the vMF concentration κ (or mixture parameters), making κ estimation ad hoc.
- Identifiability of (κ, ω) from the pushforward is not established: without conditions, κ (noise) and ω (curvature) may be confounded; formal identifiability, sensitivity, and profile-likelihood analyses are needed.
- Distribution of the averaged naive curvature is not derived: the theory gives the per-pair distribution fΩ but not the distribution (or asymptotics) of the sample average over neighbors, especially under dependence; CLTs, concentration bounds, or saddlepoint approximations are missing.
- Independence assumptions are unrealistic: tangent estimates at neighboring points often share data and are spatially correlated; the impact of correlation on the MLE and uncertainty quantification is unaddressed.
- Variable neighbor distances and anisotropic sampling are not handled: results assume constant distance ε (and often uniform angular sampling) around the base point; generalization to heterogeneous distances, anisotropy, and non-uniform point densities is open.
- Error in distance measurements is ignored in the pushforward: noisy ambient coordinates perturb ∥x − y∥ in the curvature formula; modeling and correcting for denominator noise is missing.
- Generalization beyond spheres is not provided: for non-spherical manifolds, α depends on direction via the shape operator; a derived pushforward linking directional curvature (principal curvatures/eigenvectors) to observed curvature distributions is not given.
- Only an extrinsic scalar (absolute variation curvature) is addressed: extensions to recover the full second fundamental form or shape operator (e.g., eigenvalues/eigenvectors, signs) are proposed but not developed.
- Curvature sign and directional information are lost: the “absolute variation” construction discards signs and anisotropy; methods to recover signed principal curvatures and their orientations remain open.
- Intrinsic curvature (scalar/Ricci) is not treated within this probabilistic pushforward framework: the paper discusses related literature but does not provide a pushforward-based treatment or a bridge from extrinsic AVC to intrinsic curvatures.
- Robustness to model misspecification is unstudied: while mixtures of vMF are universal approximators, practical model selection (number of components), estimation stability, and robustness under heavy-tailed or outlier-contaminated noise are not analyzed.
- Finite-sample guarantees are lacking: there are no bounds on estimator bias/variance, rates of convergence, or sample complexity for the decoded curvature estimator; asymptotic normality or confidence set construction is missing.
- Procedures for estimating κ (and mixture weights) from data are not specified: the paper posits prior knowledge or simulation-based calibration but provides no principled, data-driven estimator for κ in the presence of unknown curvature.
- Choice of neighborhood size and local sample size is not optimized: there is no guidance for selecting ε, number of neighbors q, or bandwidths to balance bias-variance trade-offs in high dimensions.
- Computational and numerical stability issues are unaddressed: evaluating high-order modified Bessel functions and optimizing the MLE in high dimensions may be unstable; complexity, conditioning, and implementation details are missing.
- Effect of high ambient codimension (n − m > 1) on bias is not quantified: empirical bias is shown to grow with dimension, but theoretical characterization of how ambient dimension and codimension drive bias is absent.
- Non-smooth manifolds and boundary effects are excluded: assumptions of smoothness and interior points are used; how corners, edges, or boundaries affect tangent estimation and curvature decoding is unknown.
- Uncertainty quantification is missing: no confidence intervals, credible intervals, or bootstrap/posterior procedures for ω (or κ) are provided; practical UQ remains open.
- Sensitivity to non-uniform sampling on the manifold is unstudied: many datasets exhibit sampling bias; its impact on tangent estimation, the induced vMF (or mixture) parameters, and decoded curvature is not analyzed.
- Real-data pipeline is incomplete: the proposed multi-phase procedure for real-world datasets (dimension estimation, noise calibration, decoding) is outlined but not implemented or validated on non-synthetic data.
- Performance under low-curvature regimes is unclear: near-flat regions (ω ≈ 0) may yield weakly informative pushforward distributions; detectability thresholds and power analyses are not provided.
- Averaging scheme and weighting are not optimized: equal weighting of directional estimates is assumed; optimal weighting (e.g., by estimated uncertainty) and its impact on decoded ω are open.
- Lack of comparisons to alternative de-biasing strategies: beyond pushforward-based MLE, other corrections (e.g., bias-corrected PCA, deconvolution, resampling-based debiasing) are not compared theoretically or empirically.
Practical Applications
Immediate Applications
The following applications can be implemented now by integrating the paper’s probabilistic decoding framework (vMF/mixture modeling, pushforward distributions, and maximum-likelihood estimation) with standard manifold-learning workflows (local PCA, neighborhood selection, and tangent-space estimation).
- Bias-aware curvature diagnostics in high-dimensional exploratory data analysis (EDA)
- Add a “decoded curvature” module to Python/R data-science stacks (e.g., scikit-learn, PyTorch, NumPy), which: (1) estimates local dimension via local PCA, (2) fits vMF or vMF-mixture noise to tangent normals, (3) computes the pushforward of angle/curvature, and (4) performs MLE to recover curvature and uncertainty.
- Provide dashboards that visualize naive vs decoded curvature and the pushforward distribution (bias profile) to guide neighborhood-size and denoising choices.
- Assumptions/dependencies: manifold hypothesis; codimension-one closed form (extend via mixtures); accurate noise calibration (κ or mixture parameters); sufficient sample density for local PCA.
- Single-cell genomics manifold analysis (e.g., scRNA-seq)
- Robust estimation of curvature along cellular manifolds to inform pseudotime trajectories, branching detection, and neighborhood size selection in diffusion-map/UMAP pipelines.
- Bias-aware comparisons across conditions (e.g., disease vs healthy) by decoding curvature rather than relying on naive estimates.
- Tools/workflows: integrate a “curvature decoding” step into Scanpy/Seurat workflows; expose uncertainty and bias diagnostics.
- Assumptions/dependencies: local dimensionality is estimable; tangent-space noise on embeddings approximated by vMF mixtures; moderate to high cell counts for stable local PCA.
- Image patch and 3D surface data (denoising, segmentation, reconstruction)
- For codimension-one surfaces (e.g., 3D point clouds), use decoded curvature to stabilize surface fitting, edge detection, and mesh refinement under noise.
- Curvature maps for shape analysis that avoid high-dimensional bias when features are added (texture/appearance).
- Tools/workflows: integrate normal estimation + vMF-mixture fitting + pushforward/MLE decoding into point-cloud processing pipelines (e.g., Open3D, PCL).
- Assumptions/dependencies: codimension-one geometry; reliable neighborhood selection for normal estimation; noise approximable by vMF mixtures.
- NLP embedding EDA (word/sentence/document embeddings)
- Curvature-informed diagnostics to identify cluster boundaries, anomalies, or representational collapse in embeddings.
- Bias-aware evaluation of model changes (fine-tuning, domain adaptation) by monitoring decoded curvature distributions.
- Tools/workflows: plug-in modules for HuggingFace/Transformers that estimate local curvature and bias profiles on embedding spaces.
- Assumptions/dependencies: manifold hypothesis holds locally; tangent-space noise can be approximated by vMF mixtures; sufficient neighborhood sizes.
- Parameter tuning and benchmarking for manifold-learning algorithms
- Use the pushforward distributions to generate synthetic benchmarks and stress tests; select neighborhood radii by minimizing curvature-estimation bias.
- Tools/workflows: add “curvature bias curves” to algorithmic evaluation suites; incorporate decoded curvature as a quality metric.
- Assumptions/dependencies: requires calibration of κ (or mixture parameters) and local dimension; validated currently on spheres and codimension-one setups.
- Sensor network and industrial IoT monitoring
- Monitor curvature drift in high-dimensional sensor embeddings to detect anomalies or regime changes (e.g., equipment degradation).
- Tools/workflows: streaming estimation of tangent spaces, vMF-mixture fitting, and decoded curvature analytics in IoT platforms.
- Assumptions/dependencies: stable manifold-like embedding of sensor states; adequate sampling density; online estimation of noise parameters.
- Teaching and scientific communication in “data geometry”
- Course modules and interactive notebooks demonstrating naive vs decoded curvature, bias growth with dimension/noise, and the role of vMF mixtures.
- Tools/workflows: Jupyter notebooks, visualization libraries; example datasets (spheres, image patches, embeddings).
- Assumptions/dependencies: none beyond availability of standard tools; supports immediate pedagogy.
Long-Term Applications
These applications require further theoretical development (arbitrary codimension, intrinsic curvature links), engineering for scale/real-time, or sector-specific validation.
- Generalized curvature decoding beyond codimension-one
- Extend the pushforward/MLE framework to Grassmannian-valued tangent spaces for arbitrary codimension; decode components of the second fundamental form and shape operator.
- Mitigate bias in intrinsic curvature estimators (scalar, Ricci, diffusion curvature) by modeling the full pipeline’s noise pushforward.
- Tools/products: generalized “CurvDecode” library (Grassmannian distributions, tensor-valued pushforwards, uncertainty quantification).
- Assumptions/dependencies: new closed-form or numerical pushforwards; robust estimation of local dimension and noise models; scalable implementations.
- Curvature-aware representation learning
- Train models with curvature regularization (e.g., penalize excessive curvature to improve generalization or stability).
- Design sampling/augmentation strategies guided by decoded curvature to cover geometric variability better.
- Tools/workflows: differentiable curvature estimators inside training loops; monitoring decoded curvature as a training metric.
- Assumptions/dependencies: differentiable approximations of curvature decoding; computational efficiency at scale.
- Robust SLAM and autonomous navigation in complex environments
- Real-time, bias-corrected curvature estimation on point clouds for surface reconstruction, obstacle classification, and path planning.
- Tools/workflows: onboard modules for tangent-space estimation and curvature decoding under sensor noise; fusion with IMU/LiDAR.
- Assumptions/dependencies: extensions to arbitrary codimensions; fast streaming estimation; hardware constraints.
- Patient trajectory modeling and clinical decision support
- Decode curvature along manifolds of patient states (EHR embeddings, phenotypes) to characterize progression, bifurcation into subtypes, and treatment response variability.
- Tools/workflows: clinical analytics pipelines with curvature-decoding modules and alerts for curvature change points.
- Assumptions/dependencies: validated manifold structure; robust noise models in clinical embeddings; longitudinal data availability.
- Regime shift detection in financial markets
- Monitor decoded curvature of market-state embeddings to detect structural breaks or volatility regimes while avoiding high-dimensional bias.
- Tools/workflows: streaming curvature estimators with uncertainty bands; integration into risk dashboards.
- Assumptions/dependencies: stable embedding construction; market noise modeling; backtesting and regulatory compliance.
- Government and policy analytics on socio-economic data
- Use decoded curvature to explore structural changes in high-dimensional indicators (employment, health, mobility) and inform interventions.
- Tools/workflows: analytics platforms that include curvature decoding and bias diagnostics; training for analysts.
- Assumptions/dependencies: domain-specific validation; transparency and interpretability requirements.
- Experimental design and data acquisition planning
- Use the framework to set target sampling densities and noise levels that yield reliable curvature estimates for forthcoming experiments (e.g., imaging, sensors, omics).
- Tools/workflows: simulation-based planners leveraging pushforward distributions to quantify expected bias and confidence.
- Assumptions/dependencies: accurate pre-experiment noise/density models; domain-specific manifold priors.
- Privacy and fairness auditing of representation spaces
- Assess whether model representations exhibit curvature pathologies (e.g., representational collapse or overly sharp cluster boundaries) that correlate with demographic subgroups.
- Tools/workflows: decoded-curvature probes integrated into fairness audits; longitudinal monitoring of curvature changes after retraining.
- Assumptions/dependencies: careful linkage between geometry and fairness outcomes; validated protocols.
Across both immediate and long-term uses, the most critical dependencies are: (1) the manifold hypothesis and reliable local dimension estimation; (2) accurate characterization of tangent-space noise (vMF/mixture parameters) and neighborhood radius selection; (3) sufficient sampling density; and (4) extensions of the pushforward framework to arbitrary codimensions and to intrinsic curvature measures for broader generalization.
Glossary
- Absolute variation curvature: An extrinsic curvature measure capturing average change in tangent space orientation around a point. "We set ourselves the goal of estimating a quantity we call the {\em absolute variation curvature}, , which measures the variation in relative tangent space orientation near a given point (cf., Section~\ref{sec:curv})."
- Codimension: The difference between ambient space dimension and manifold dimension. "Although the form of our results depends on working with a codimension one embedding, our technique suggests a natural extension to the setting of arbitrary codimension."
- Diffusion curvature: A curvature notion defined via probabilities of random walks remaining within a region after a number of steps. "This is in turn related to {\em diffusion curvature} \cite{DiffusionCurvatureNIPS} which defines curvature (at a given point ) in terms of the probability that a random walk stays within a given volume after a fixed number of steps, a formalism that comes from the foundational work that introduced the notion of {\em diffusion maps} to high-dimensional data analysis \cite{coifman2006diffusion}."
- Diffusion maps: A spectral method for analyzing high-dimensional data using a diffusion process on a graph. "a formalism that comes from the foundational work that introduced the notion of {\em diffusion maps} to high-dimensional data analysis \cite{coifman2006diffusion}."
- Extrinsic curvature: Curvature dependent on the embedding, measuring how tangent space orientation changes in the ambient space. "{\em Extrinsic curvature} gives a measure of local deviation of the tangent space, in essence asking how the orientation of the tangent space changes near a point."
- Frechet mean: The point on a manifold minimizing expected squared distance to a random variable (a generalization of the Euclidean mean). "with (Frechet) mean of "
- Grassmannian: The manifold of all m-dimensional linear subspaces of an n-dimensional space. "For a general submanifold of dimension , the tangent spaces are identified with points on a Grassmannian ."
- Grassmannian-valued random variable: A random variable whose outcomes are linear subspaces (points on a Grassmannian). "We treat the tangent space approximation as a Grassmannian valued random-variable."
- Intrinsic curvature: Curvature determined by the manifold’s metric, independent of any embedding. "{\em Intrinsic curvature} is a notion of curvature that is independent of embedding and solely relies on the metric structure."
- Manifold hypothesis: The assumption that high-dimensional data lie near a low-dimensional manifold in the ambient space. "The ``manifold hypothesis" assumes that a data cloud can be viewed as noisy samples of an underlying manifold."
- Mixture of vMF distributions: A weighted combination of von Mises–Fisher distributions used to model complex directional noise. "Since any noise model can be well-approximated by a finite mixture of vMF distributions, our result applies more generally (Theorem 4)"
- Modified Bessel function of the first kind: A special function appearing in the normalization and densities of certain distributions (e.g., vMF). "and is modified Bessel function of the first kind."
- Ollivier-Ricci curvature: A discrete/metric measure of curvature based on contraction of probability measures under random walks. "The latter relates it {\em Ollivier-Ricci curvature} which is derived from a measure comparing nearby random walks on the manifold \cite{OLLIVIER2009810}."
- Pushforward: The transformation of a probability distribution under a mapping, yielding the distribution of a derived quantity. "This ``pushforward" of the original noise distribution encodes detailed information about the empirical estimate."
- Ricci curvature: An intrinsic curvature that captures average volume distortion along geodesics; relates to growth of geodesic balls. "{\em Ricci curvature} is another intrinsic curvature measure derived from the relative (with respect to Euclidean space) asymptotic growth of balls centered on the point of interest."
- Scalar curvature: A single value summarizing curvature at a point, often the trace of the Ricci tensor; compares local volume to Euclidean. "The papers \cite{hickok2023} and \cite{RiemannianCurvaturePNAS} give two approaches to the calculation of scalar curvature."
- Second fundamental form: A tensor describing the extrinsic second-order geometry (how the manifold bends in the ambient space). "More generally, the {\em second fundamental form} is a tensor that encodes all of the second order local behavior"
- Shape operator: A linear operator related to the second fundamental form that maps tangent vectors to curvature directions. "the second fundamental form and the shape operator so that in principle our general framework can be applied to other ``derivative" forms of curvature."
- Tangent space: The linear approximation of a manifold at a point, consisting of all tangent directions at that point. "This is effectively the estimation of the tangent space at a point."
- von Mises-Fisher (vMF) distribution: A probability distribution on the sphere parameterized by a mean direction and concentration. "Initially, we assume that is distributed according to a von Mises-Fisher distribution (vMF) with the density"
Collections
Sign up for free to add this paper to one or more collections.