E-Scores for (In)Correctness Assessment of Generative Model Outputs (2510.25770v1)
Abstract: While generative models, especially LLMs, are ubiquitous in today's world, principled mechanisms to assess their (in)correctness are limited. Using the conformal prediction framework, previous works construct sets of LLM responses where the probability of including an incorrect response, or error, is capped at a desired user-defined tolerance level. However, since these methods are based on p-values, they are susceptible to p-hacking, i.e., choosing the tolerance level post-hoc can invalidate the guarantees. We therefore leverage e-values to complement generative model outputs with e-scores as a measure of incorrectness. In addition to achieving the same statistical guarantees as before, e-scores provide users flexibility in adaptively choosing tolerance levels after observing the e-scores themselves, by upper bounding a post-hoc notion of error called size distortion. We experimentally demonstrate their efficacy in assessing LLM outputs for different correctness types: mathematical factuality and property constraints satisfaction.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about a simple way to check if answers from generative AI models (like chatbots and LLMs, or LLMs) are correct or not. The authors introduce “e-scores,” which are numbers attached to each AI answer that act like a “incorrectness meter.” Small e-scores suggest the answer is likely correct, and large e-scores suggest it’s likely wrong. The cool part is that these scores come with solid statistical guarantees, even if you decide your tolerance level after seeing the scores.
Key Objectives
The paper aims to solve a practical problem: people often want to choose how strict they are about AI answers after they see those answers. Previous methods used “p-values,” which only give guarantees if you set your tolerance level in advance. The authors’ goals are:
- Create a scoring method (e-scores) that still provides reliable guarantees even when you pick your tolerance level afterward.
- Make the method work for any generative model, not just specific LLMs.
- Check not just full answers, but also partial steps (like steps in a math solution), because sometimes early steps are correct even if later ones are wrong.
Methods and Approach
The challenge in simple terms
- Imagine you have a bunch of AI answers to a question. You want a safe way to pick which ones to keep.
- You pick a tolerance level, called alpha (). Think of as a safety setting: smaller means you’re more strict.
- Old methods use p-values and say “the chance of including a wrong answer is at most ,” but only if you set before seeing the data. If you change after looking (“post-hoc”), those guarantees can break. That’s similar to moving the goalposts after the game starts—sometimes called “p-hacking.”
What are e-values and e-scores?
- An e-value is a number built so that, on average, it doesn’t exceed 1 under the assumption of “no error.” That property lets us safely choose after seeing the data.
- The authors convert e-values into “e-scores,” which are easy to interpret: low means “looks correct,” high means “looks incorrect.”
Size distortion: a safer guarantee
- Instead of promising “error rate ≤ ” directly, the authors control something called “size distortion.” In plain terms, it’s the expected ratio of “did we include a wrong answer?” to your chosen tolerance . They prove this expected ratio is ≤ 1, even if you choose after seeing the scores.
- Put simply: you can set your strictness level post-hoc, and the system still behaves fairly.
How do they compute e-scores?
- They use “calibration data,” which is a set of past examples where we know which answers are correct and which are wrong.
- They build an “oracle estimator” (think: a helper model) that guesses how likely an answer is correct. If answers have multiple steps (like chain-of-thought in math), they can estimate correctness step by step and multiply the probabilities to get a full-answer score.
- They compare the test answer’s “correctness signal” to the worst incorrect signals seen in the calibration set. This comparison produces an e-score that reflects how risky the answer is.
What counts as a “response”?
- A response can be the full message or partial steps (like step 1, step 1+2, …). This is helpful because sometimes the first steps are right even if later ones fail.
- The paper even allows reordering the steps in theory, to consider a very large set of possible partial responses, making the method more flexible for different applications.
Main Findings and Why They Matter
Across two types of tests, the e-scores worked well:
- Mathematical factuality (ProcessBench)
- The model’s step-by-step math solutions were checked.
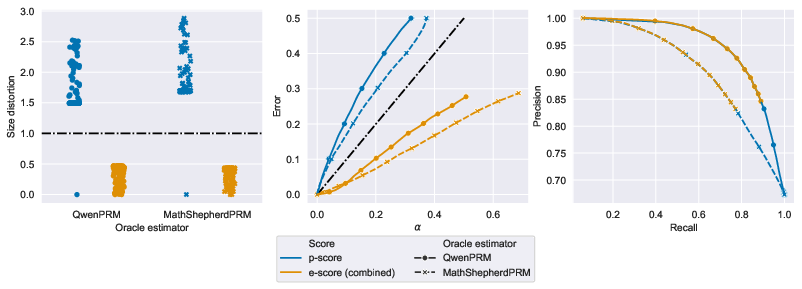
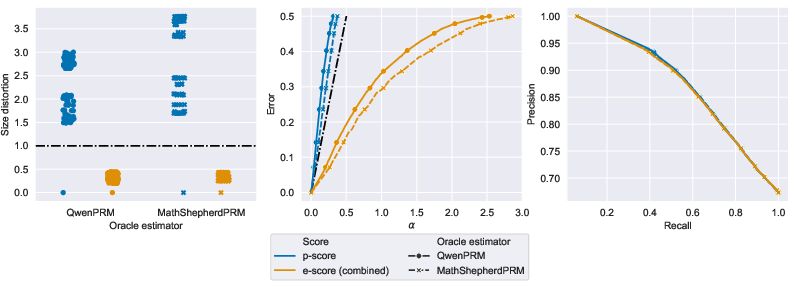
- E-scores kept the “size distortion” under control (≤ 1), as promised.
- E-scores tended to have error less than or about equal to the chosen , which is what you want.
- Precision and recall (keeping correct answers vs. throwing out too many) were comparable to older p-value methods, with e-scores being slightly more cautious.
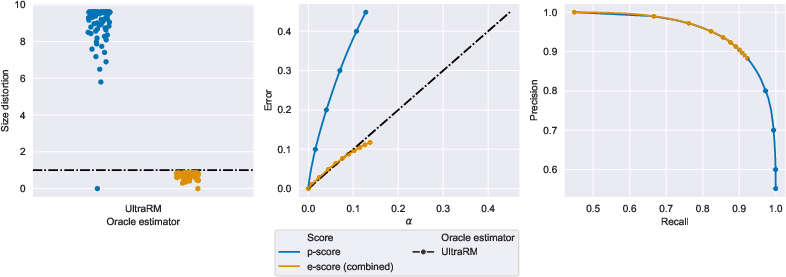
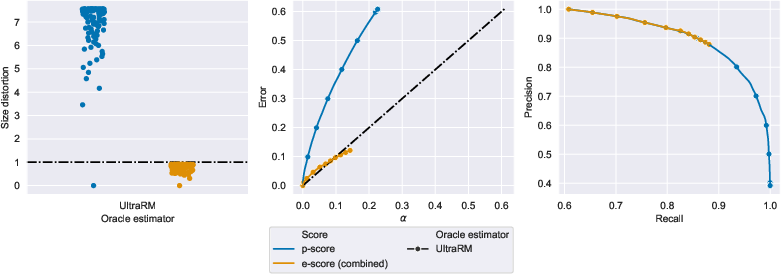
- Property constraints satisfaction (UltraFeedback)
- Answers were checked for traits like instruction-following, helpfulness, truthfulness, and honesty.
- Again, e-scores kept size distortion ≤ 1 and maintained solid precision/recall, while handling post-hoc choices safely.
Other useful observations:
- E-scores are faster to compute in practice than p-scores because they pre-summarize the calibration data once, rather than doing ranking comparisons for every test case.
- The choice of the “oracle estimator” matters: better estimators lead to better precision/recall when filtering answers.
Implications and Potential Impact
This work makes it safer and easier to use AI-generated answers in real life:
- You can choose how strict to be after seeing the scores without breaking the guarantees. This fits real-world behavior, where people naturally adjust thresholds after looking at results.
- It reduces risks of “p-hacking” by switching from p-values to e-values.
- It works for many kinds of generative models and different forms of responses, including step-by-step reasoning.
- It could be used in education (checking math steps), content moderation (enforcing properties like honesty), or any setting where you need trustworthy AI outputs.
In the future, improving the oracle estimator (the helper that predicts correctness) would make the system even more reliable, and exploring other post-hoc error measures might broaden the guarantees further.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of unresolved issues and concrete open directions that emerge from the paper’s assumptions, design choices, theory, and experiments.
- Assumption of exchangeability: Guarantees rely on calibration and test prompts being exchangeable, which is fragile under domain shift, temporal drift, curated prompt selection, or feedback-driven deployments. How to obtain post-hoc-valid guarantees under covariate shift or non-exchangeable data (e.g., covariate-conditional or covariate-shift robust e-scores)?
- Oracle estimator independence: The method assumes the oracle estimator is trained on data independent from both calibration and test. How sensitive are guarantees and power to mild dependencies, partial overlap, or leakage? Can one design data-splitting or cross-fitting strategies with provable post-hoc validity?
- Mis-specification of oracle estimator: Theoretical guarantees hold in expectation even if the oracle proxy is inaccurate, but power can degrade. What are quantitative sensitivity/robustness bounds on size distortion and inclusion rates as a function of estimator calibration error or AUC?
- Distributional robustness: No analysis is provided for adversarial or worst-case prompts, adversarially crafted chain-of-thoughts that “game” the oracle estimator, or prompt injection that targets the verifier. Can one design adversarially robust e-scores or certify worst-case robustness?
- Conditional guarantees: The results are marginal (average over prompts). Can one provide conditional guarantees (e.g., coverage conditional on prompt features, topic/domain subgroup guarantees) to address fairness or domain-specific reliability?
- Multiple testing and repeated use: The paper addresses per-prompt post-hoc α, but not composition across many prompts/users, repeated queries, or dashboards that adapt on historical e-scores. How do error guarantees compose across batches, time, or interactive sessions? Can anytime-valid/online e-processes be leveraged here?
- Family-wise error and FDR control: The work controls size distortion for inclusion of any incorrect response per prompt. How to extend to classical error rates (FWER/FDR) when selecting multiple responses across many prompts?
- Optional stopping and monitoring: E-values can support optional stopping, but the proposed procedure is not analyzed in settings with sequential monitoring over growing response sets or iterative refinement (e.g., self-correction loops). Can one derive time-uniform or sequential guarantees for this use case?
- Scope of response sets: The theory allows a super-set including all permutations of sub-responses, but experiments use a restricted set and do not paper computational feasibility or benefits of permutation-closed sets. What are practical algorithms to construct/use large response sets for long chains without prohibitive cost?
- Single-sample generation: The response set is built from a single generated trajectory. How to extend guarantees to multiple candidate responses (e.g., beam search, diverse sampling, n-best lists) and to aggregate over them with post-hoc α while keeping validity?
- Dependence across sub-responses: The framework treats sub-responses but does not analyze dependencies or segmentation errors (e.g., incorrect step boundaries from an LLM segmenter). How do segmentation errors impact size distortion and precision/recall?
- Choice of f and extremal aggregation: Using f* as the maximum incorrect calibration score is conservative and sensitive to outliers, especially for small n. Are there alternative aggregations (trimmed maxima, quantiles, shrinkage, regularized f*) that retain validity while improving power?
- Smoothing and numerical stability: When calibration contains few or no incorrect examples (f*≈0), the denominator can induce very large e-scores, harming utility. Can smoothing (e.g., additive constants, prior pseudo-counts) be introduced with preserved post-hoc validity?
- Combining multiple oracle estimators: The paper averages e-values across three monotone transformations, but not across distinct verifiers (e.g., multiple PRMs/judges). How to combine dependent e-values from multiple verifiers (e.g., safe merging, dependence-robust combinations) to improve power?
- Training oracle estimators for power: There is no guidance on how to train verifiers to maximize power (precision/recall) of e-scores while preserving validity. What training objectives (e.g., proper scoring rules, calibration-focused losses) and architectures yield the best trade-offs?
- Alternative post-hoc error notions: The work focuses on size distortion. How do e-scores fare under other post-hoc-valid criteria (e.g., risk-controlling prediction sets, conformal-type conditional risk, size–power trade-offs in Koning et al.)? Can guarantees be extended to these alternatives?
- Per-instance vs expected guarantees: Guarantees are in expectation; some applications need high-probability or per-instance assurances. Can one derive concentration bounds or confidence sequences for distortion at the prompt level?
- User-facing calibration of α: E-scores can exceed 1; user strategies restrict α≤1 in some experiments, affecting recall. What are principled mappings or interfaces for user-selected α that preserve interpretability, utility, and validity across tasks?
- Label noise and ambiguity: Benchmarks (e.g., UltraFeedback, ProcessBench) include noisy or subjective labels (e.g., GPT-4 ratings, earliest-error annotations). What is the impact of label noise on e-scores, and can noise-robust verifiers or probabilistic label models improve guarantees?
- Domain and modality generalization: Experiments are limited to math and text property constraints. How does the method extend to other tasks (code generation, retrieval-augmented generation, multi-modal LLMs), and what adaptations are needed for non-text or structured outputs?
- Computational trade-offs for large response sets: While e-scores amortize calibration cost, scaling to very large response sets (long chains, multi-sample generation) and dynamic updates is unaddressed. What data structures or streaming algorithms enable real-time scoring with evolving calibration sets?
- Calibration data acquisition: The approach requires labeled calibration sets potentially expensive to obtain. How to minimize labeling via active learning, weak supervision, or semi-supervised verification while maintaining exchangeability and validity?
- Distribution selection for calibration: No guidance is given for selecting calibration prompts to match anticipated test distributions. Can one design calibration set selection or weighting to optimize power under constrained labeling budgets?
- Fairness and subgroup effects: No analysis of whether e-scores differentially include/exclude responses across demographic or topical subgroups. How to audit and enforce subgroup-valid guarantees?
- Comparison breadth: Baselines are primarily p-scores. Missing comparisons include other post-hoc-valid frameworks (e.g., confidence sequences, risk-controlling prediction sets, selective inference) and e-process designs beyond simple averaging.
- Downstream utility evaluation: The paper evaluates error/precision/recall but not downstream task utility (e.g., user success rates, task completion times, or cost of excluded correct responses). Can one integrate utility-aware α selection with validity guarantees?
- Robustness to generation settings: The impact of decoding parameters (temperature, nucleus sampling), model size, and alignment on e-score behavior is unexplored. How do these factors affect calibration stability and power?
- Handling partial credit: Many tasks admit partially correct responses; the binary oracle ignores graded correctness. Can e-scores be extended to ordinal/continuous correctness with meaningful guarantees?
- Open-source implementations and reproducibility: While high-level complexity is discussed, there is no public ablation on implementation choices (e.g., f-transform selection, segmentation strategy). A reference implementation with reproducible pipelines would enable broader validation.
These points suggest concrete avenues for future research on strengthening theoretical robustness, expanding applicability, improving power and practicality, and ensuring fair and interpretable deployment of e-scores in real-world generative model assessments.
Practical Applications
Practical Applications of “E-Scores for (In)Correctness Assessment of Generative Model Outputs”
The paper introduces e-scores—reciprocal e-values—as data-dependent measures of incorrectness for generative models, delivering post-hoc statistical guarantees via size distortion control. Below are actionable applications across sectors, organized by immediacy and feasibility. Each bullet includes potential tools/workflows and key dependencies that affect deployment.
Immediate Applications
- LLM output vetting and guardrails in production (software, enterprise IT)
- What: Attach e-scores to every LLM response (and sub-response/step) to filter outputs using adaptive thresholds after viewing scores; select the longest correct prefix; gate risky content.
- How: “E-Score Guardrail SDK” integrated as a middleware layer; dashboards to monitor size distortion and error vs. alpha; use fractional inclusion or max-constrained alpha strategies.
- Dependencies: Availability of a domain-appropriate oracle estimator ; representative, labeled calibration data that is exchangeable with production prompts; operational threshold policies.
- Math tutoring and assessment (education)
- What: Step-wise correctness assessment for chain-of-thought reasoning; surface e-scores per step to guide feedback and grading; accept partially correct solutions backed by guarantees.
- How: Integrate PRMs (e.g., QwenPRM, MathShepherdPRM) to compute ; e-score filtering for step acceptance; teacher dashboards displaying size distortion metrics.
- Dependencies: Quality of math-specific oracle models; calibration sets matching course content; UI/UX that explains adaptive thresholds to educators and students.
- Code generation safety and review (software engineering)
- What: Use e-scores to triage AI-generated code suggestions; accept only suggestions with low incorrectness scores; fall back to correct partial prefixes.
- How: IDE plugins running the e-score pipeline on code blocks; configurable post-hoc alpha policies per repository; audit logs of size distortion per deployment.
- Dependencies: Code-specific oracle estimators (e.g., static analyzers or specialized verifier models); labeled calibration data from codebases; robust handling of sub-responses (code chunks).
- Content moderation and knowledge base curation (media, knowledge management)
- What: Filter generated answers/articles by truthfulness/honesty properties; e-score-based inclusion to build high-integrity knowledge bases or moderated content feeds.
- How: Use property reward models (e.g., UltraRM with sigmoid) as ; batch fractional inclusion for large-scale ingestion; dashboards tracking precision–recall and error vs. alpha.
- Dependencies: Property-specific oracles; calibration sets that reflect target domains; clear policies for allowable error rates.
- Customer support and agent assist (contact centers)
- What: Gate auto-drafted replies by e-scores on instruction-following/helpfulness; allow agents to post-hoc tighten tolerance when needed (e.g., in high-stakes interactions).
- How: Workflow buttons that adjust post-hoc alpha after previewing e-scores; partial inclusion of safe response segments; escalation when scores exceed thresholds.
- Dependencies: Reliable oracle estimators for support domains; calibration data sampled from recent ticket distributions; training agents to interpret e-scores.
- AI governance, compliance, and audit (policy, risk management)
- What: Track and report size distortion as a post-hoc guarantee metric for LLM deployments; establish risk budgets and adaptive thresholds aligned with regulations (e.g., EU AI Act).
- How: “E-Score Monitor” dashboards; periodic calibration refresh; audit-ready logs with alpha decisions and observed errors; standardized governance playbooks.
- Dependencies: Governance acceptance of e-value based guarantees; calibration data lifecycle management; organization-wide policies for post-hoc thresholding.
- Research evaluation and benchmarking (academia)
- What: Replace p-score conformal filters with e-scores to avoid p-hacking and support post-hoc alpha selection in LLM evaluation pipelines.
- How: Incorporate e-score computation into benchmark harnesses (e.g., ProcessBench-like setups); report size distortion and precision–recall alongside task metrics.
- Dependencies: Public availability of labeled calibration sets; reproducible oracle estimators per task; community standards for reporting post-hoc guarantees.
- Retrieval-augmented generation QA (software, information retrieval)
- What: Use e-scores to gate claim-level outputs in RAG workflows; only include sentences with low incorrectness scores; adapt thresholds based on query sensitivity.
- How: Sentence-level with aggregation to response-level e-scores; fractional inclusion to keep top fraction of sentences; dynamic alpha per query risk profile.
- Dependencies: High-quality claim verifiers; calibration data that matches retrieval domains; granular handling of sub-responses (sentences).
- Personal productivity assistants (daily life)
- What: Display e-scores for suggestions (e.g., email drafts, to-do instructions), letting users tighten or relax post-hoc thresholds depending on task importance.
- How: UI indicators showing confidence via e-scores; quick toggles for alpha; default use of the longest safe partial response.
- Dependencies: Lightweight oracle estimators for general tasks; background calibration built from typical user prompts; user education on confidence cues.
- Data pipeline hygiene for training (ML ops)
- What: Filter synthetic or weakly labeled data with e-scores to retain high-correctness examples for SFT/RLHF; maintain datasets with measured size distortion.
- How: Batch scoring with amortized calibration; dataset dashboards showing error vs. alpha; policies for acceptable distortion thresholds per training phase.
- Dependencies: Task-specific oracles; sufficiently large calibration sets; clear training objectives aligned with properties to be enforced.
Long-Term Applications
- Sector-specific high-stakes deployments (healthcare, legal, finance)
- What: E-score guarantees on clinical note drafting, legal brief assistance, and financial reporting; adaptive thresholds in workflows with human oversight.
- How: Specialized oracle estimators (clinical fact checkers, legal citation verifiers, financial compliance checkers); integrated e-score guardrails in domain tools.
- Dependencies: Domain-validated oracles with high accuracy; large, representative, labeled calibration datasets; regulatory buy-in for e-value-based assurances.
- Autonomous agents with adaptive risk gating (robotics, software agents)
- What: Use e-scores to gate sequential plans/actions step-by-step; dynamically adjust alpha based on context and uncertainty; prevent unsafe execution cascades.
- How: Step-level e-score computation for plans; safety overseers that modulate thresholds; integration with time-uniform e-value techniques for online control.
- Dependencies: Robust plan-verifier oracles; streaming calibration strategies; real-time inference constraints and explainability.
- Cross-modal generative systems (vision, audio, multimodal)
- What: Extend e-score framework to image captions, audio transcriptions, and multimodal reasoning; post-hoc thresholds for correctness across modalities.
- How: Multimodal oracles (e.g., vision-language verifiers) producing ; response-set permutations adapted to multimodal segments; combined e-score ensemble.
- Dependencies: Accurate multimodal verifiers; calibration data spanning modalities; engineering for segment-level scoring and aggregation.
- Standardization and certification (policy, industry consortia)
- What: “E-Score Certified” labels for products meeting size distortion criteria; standardized reporting schemas for post-hoc alpha decisions and guarantees.
- How: Industry bodies define acceptable distortion bounds; certification pipelines audit calibration and oracle quality; compliance frameworks adopt metrics.
- Dependencies: Consensus standards; third-party auditors; longitudinal evidence of effectiveness.
- Adaptive training and curriculum learning (ML research, productized training)
- What: Use e-scores as feedback signals to prioritize learning from high-correctness examples; curriculum schedules adapting thresholds during training phases.
- How: Training pipelines incorporate e-score filtering; reward shaping based on incorrectness measures; ablations on generalization and robustness.
- Dependencies: Stable interaction between training dynamics and e-score filters; availability of oracles during training; compute trade-offs.
- Ensemble verification and oracle fusion (advanced tooling)
- What: Combine multiple oracles (e.g., PRMs, retrieval verifiers, rule engines) via admissible e-value averaging to produce robust e-scores across criteria.
- How: Oracle fusion layer outputs combined e-scores; domain-specific weighting; confidence calibration for heterogeneous signals.
- Dependencies: Interoperable oracle APIs; procedures for weighting and validation; monitoring for drift and failure modes.
- Real-time streaming moderation and governance (platforms)
- What: Continuous e-score gating for live content (social/video platforms) with post-hoc adjustments to risk budgets during events.
- How: Low-latency e-score computation; dashboards for dynamic alpha allocation; incident response tied to distortion metrics.
- Dependencies: Efficient oracle inference; scalable calibration updates; platform policies enabling rapid post-hoc changes.
- Public-sector deployments with adaptive assurance (policy, govtech)
- What: Post-hoc thresholding to meet varying risk tolerances in citizen-facing services (e.g., benefit explanations, tax guidance), with transparent guarantees.
- How: Gov-grade oracles trained on public policy knowledge; e-score reporting in public dashboards; community oversight of alpha policies.
- Dependencies: Trusted oracles; representative calibration sampling across demographics; clear communication of guarantees.
- Safety-critical planning in industrial systems (energy, manufacturing)
- What: E-score-based filtering of AI-generated procedures, maintenance steps, and incident responses; prefer validated partial plans over risky full outputs.
- How: Integration with digital twins and procedure verifiers; stepwise thresholds per operational state; audit logs of distortion during incidents.
- Dependencies: High-fidelity oracles aligned with physical constraints; rigorous calibration against operational scenarios; safety case documentation.
- Education platforms with verified reasoning (large-scale edtech)
- What: Platform-wide adoption of e-scores to ensure correctness in explanations and solutions; adaptive difficulty and feedback guided by measured incorrectness.
- How: PRM-backed oracles for diverse curricula; batch fractional inclusion to keep high-quality content; student-facing confidence cues.
- Dependencies: Broad coverage of oracle models across subjects; periodic recalibration; pedagogical validation of scoring and thresholds.
Common Assumptions and Dependencies Across Applications
- Oracle estimator quality: The strength of guarantees hinges on the accuracy and domain relevance of ; pre-trained PRMs or reward models may need domain-specific training.
- Calibration–test exchangeability: Statistical guarantees require calibration prompts/responses to be representative of test usage; periodic recalibration may be necessary.
- Labeled calibration data: Enough labeled examples (including incorrect ones) are needed; data collection and annotation costs must be planned.
- Threshold policies and UX: Post-hoc alpha selection must be well-documented, explainable, and aligned with risk tolerance; user interfaces should make confidence understandable.
- Computational considerations: E-scores are amortized and cheaper than p-scores, but oracle inference costs can dominate; optimize for batch scoring and streaming when needed.
- Legal and compliance constraints: Sector deployments (e.g., healthcare, finance, public sector) require alignment with regulations and documented assurances of statistical guarantees.
Glossary
- admissible e-value: An e-value that cannot be uniformly improved by any other e-value; a notion of optimality in e-value combinations. "simple averaging of e-values yields an admissible e-value"
- approximate deducibility graph: A graph structure that captures inferred dependencies among sub-responses; used to define valid orderings of steps. "topological orderings of an approximate deducibility graph"
- auto-regressive models: Generative models that produce outputs sequentially, where each token depends on previous tokens. "While natural for auto-regressive models, we do not assume any particular dependency structure."
- calibration data: Labeled data used to calibrate statistical procedures so that test-time guarantees hold under exchangeability. "we are given labeled calibration data that is assumed to be exchangeable with the test data"
- chain-of-thought reasoning: A prompting and generation technique where models produce explicit step-by-step reasoning. "steps in chain-of-thought reasoning"
- conformal prediction: A framework that provides distribution-free, finite-sample guarantees by constructing prediction sets using calibration data. "These methods rely on p-value based conformal prediction"
- e-scores: Scores based on e-values that measure incorrectness of generated responses; low for correct and high for incorrect. "We propose e-scores as measures of incorrectness"
- e-values: Nonnegative statistics satisfying an expected value bound, often used for safe, post-hoc valid inference. "We therefore leverage e-values to complement generative model outputs with e-scores as a measure of incorrectness."
- e-variable: A nonnegative random variable R with , which yields valid post-hoc error control via Markov’s inequality. "And, it is an e-variable if "
- exchangeable data: Data whose joint distribution is invariant under permutations; a key assumption for conformal/e-value guarantees. "construct e-values for supervised learning under exchangeable data"
- fractional inclusion: A strategy to include a specified fraction of responses by adapting the tolerance level post-hoc. "consider a functional that can vary to improve fractional inclusion"
- Markov's inequality: A probabilistic inequality giving bounds on tail probabilities using expectations, enabling e-value to p-type bounds. "which, with Markov's inequality, gives $P{\nicefrac{1}{R} \leq \alpha} \leq \alpha$"
- nested conformal framework: A variant of conformal prediction that uses nested sets or ranks to construct valid filtered sets. "their use of the nested conformal framework"
- non-conformity functions: Functions that score how “strange” or nonconforming a response is, used to build conformal p-values/scores. "similar to the non-conformity functions"
- oracle: A (possibly hypothetical) labeling function that determines the correctness of a response for a given prompt. "we define (in)correctness with respect to an oracle "
- oracle estimator: A learned or heuristic model that approximates the oracle’s correctness judgment, often producing probabilities. "The oracle estimator approximates the oracle "
- p-hacking: Post-hoc manipulation of significance thresholds or analyses that invalidates nominal statistical guarantees. "susceptible to p-hacking"
- p-scores: Scores derived from p-values (often as ranks) used to filter responses under conformal prediction. "we compare against p-value based scores, or p-scores."
- p-values: Probabilities under a null model of seeing results as extreme or more, traditionally used for hypothesis testing. "While p-values have been used for hypothesis testing for almost a century"
- p-variable: A nonnegative random variable R with for all , generalizing the notion of a valid p-value. "It is a p-variable if "
- post-hoc : A data-dependent tolerance level chosen after seeing the scores, requiring special care for valid guarantees. "called post-hoc "
- property constraints satisfaction: Ensuring generated responses meet specified properties (e.g., truthfulness, helpfulness) formalized as constraints. "property constraints satisfaction, where we ensure responses satisfy certain desirable properties."
- size distortion: The expected ratio between the observed error (inclusion of incorrect responses) and the chosen tolerance level, controlled to be ≤1. "provide statistical guarantees on a post-hoc notion of error called size distortion"
- topological orderings: Orderings of nodes in a directed acyclic graph consistent with edge directions, used to structure response steps. "topological orderings of an approximate deducibility graph"
Collections
Sign up for free to add this paper to one or more collections.