An efficient probabilistic hardware architecture for diffusion-like models (2510.23972v1)
Abstract: The proliferation of probabilistic AI has promoted proposals for specialized stochastic computers. Despite promising efficiency gains, these proposals have failed to gain traction because they rely on fundamentally limited modeling techniques and exotic, unscalable hardware. In this work, we address these shortcomings by proposing an all-transistor probabilistic computer that implements powerful denoising models at the hardware level. A system-level analysis indicates that devices based on our architecture could achieve performance parity with GPUs on a simple image benchmark using approximately 10,000 times less energy.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about building a new kind of computer for AI that uses randomness on purpose to work more efficiently. The authors propose an all-transistor “probabilistic computer” that runs denoising models directly in hardware. They argue that this kind of machine could generate images about as well as a regular GPU-based system but use roughly 10,000 times less energy. The big idea is to match powerful AI methods (like diffusion models) with hardware designed specifically for probability and randomness, instead of forcing AI to run on GPUs that were originally made for graphics.
Key Objectives and Questions
The paper sets out to explore a few simple questions:
- Can we make a practical, scalable probabilistic computer using only standard transistors (no exotic parts)?
- Can we avoid a major problem that slows down older probabilistic models by switching to a “denoising” approach?
- How does such a system compare to common AI methods on GPUs in terms of image quality and energy use?
Methods and Approach
To understand the approach, here are the core ideas explained in everyday language:
The problem with older probabilistic models (EBMs)
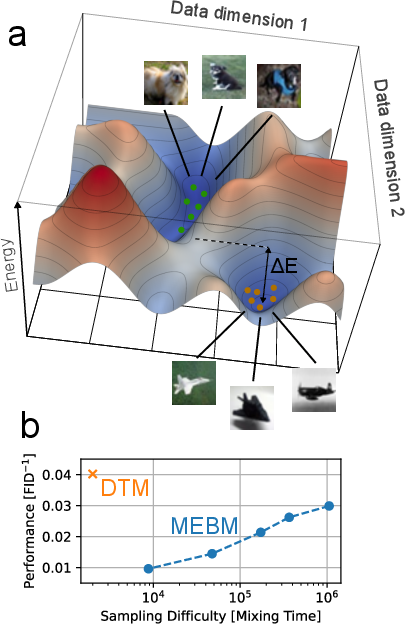
- Energy-Based Models (EBMs) describe data by shaping a “landscape” with hills and valleys. Good data points sit in low-energy valleys; bad or unlikely points sit on high-energy hills.
- When the data has many distinct clusters (like pictures of dogs vs. airplanes), the landscape becomes rugged: deep valleys separated by tall mountains.
- To generate a new sample, the computer “walks” randomly across this landscape. But moving uphill is unlikely, so crossing mountains takes a very long time. This is called the mixing-expressivity tradeoff: the better the model fits complex data, the harder and slower it is to sample from it.
Think of it like trying to wander from one valley to another by random steps without enough energy to climb the mountain in between—it’s painfully slow.
The fix: Denoising Thermodynamic Models (DTMs)
- Instead of using one tough model to do everything, DTMs use a chain of simpler steps that “clean” noise gradually, like restoring a fuzzy picture step by step until it’s clear.
- This is similar to diffusion models (used in modern image generators), which turn random noise into images by making many small improvements.
- Each step in the chain uses an EBM, but because the step is small, the energy landscape is easy to sample. By chaining many simple steps, you can still learn complex data distributions without getting stuck.
- DTMs can also add “latent variables” (extra hidden helpers) so the model can grow in power without becoming too hard to sample.
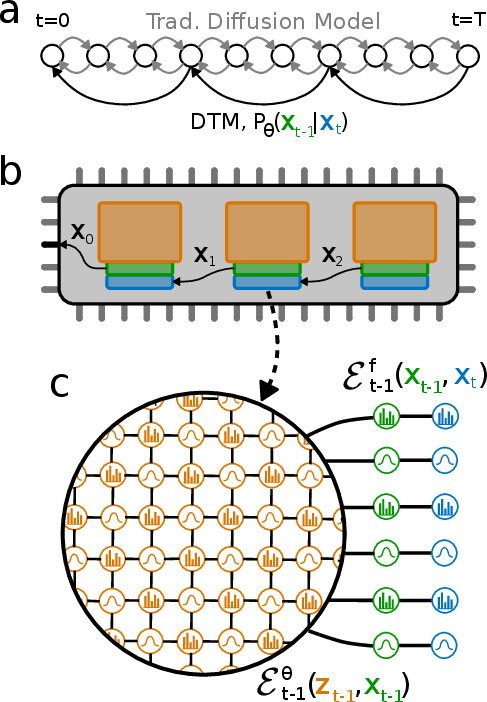
Hardware design: a denoising computer made of transistors
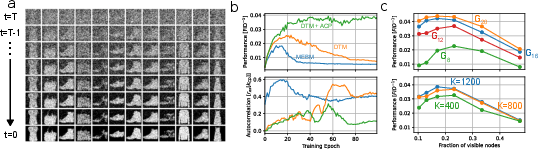
- The authors propose the Denoising Thermodynamic Computer Architecture (DTCA), which chains many simple hardware-based EBMs to perform the denoising steps.
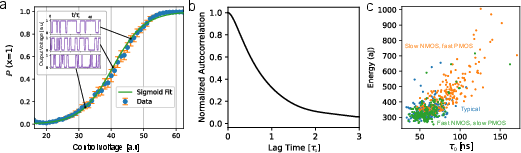
- The core building block is an all-transistor random-number generator (RNG). It uses tiny natural jitters in transistors to produce random bits, and you can “bias” it by changing a voltage—making it more likely to output a 1 or a -1. The response looks like a smooth “S-curve” (a sigmoid).
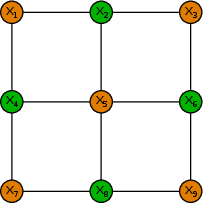
- The model inside the hardware is a Boltzmann machine: a grid of binary variables (bits) that flip randomly based on their neighbors. A simple update rule (called Gibbs sampling) handles the flipping. Because the grid can be split into two color groups, many bits can be updated in parallel—great for speed and energy.
- The authors tested the RNG circuit in the lab and simulated the whole DTCA system on GPUs to measure performance while estimating the energy it would use if built in hardware.
Training and stability
- They train DTMs by sampling from the model and using those samples to adjust the parameters—a standard Monte Carlo approach.
- DTMs are more stable to train than single big EBMs because each step’s sampling is easier.
- To keep things stable as models grow, they add an Adaptive Correlation Penalty (ACP): a feedback tool that watches how “stuck” the sampler is and gently pushes the model to stay sampleable. This keeps gradients accurate and training smooth.
Main Findings and Why They Matter
Here are the main results the paper reports, and why they’re important:
- DTMs avoid the old sampling problem: Chaining many easy steps breaks the link between “model power” and “sampling difficulty.” You can make the model stronger without grinding sampling to a halt.
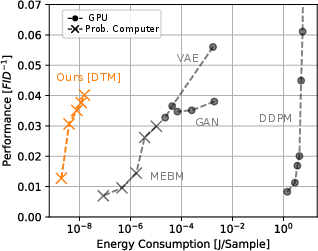
- Huge energy savings: On a simple image benchmark (binarized Fashion-MNIST), their denoising probabilistic computer is predicted to match the best GPU-based method’s image quality while using about 10,000 times less energy per generated image.
- Practical hardware: Their all-transistor RNG is small, fast (about 100 nanoseconds correlation time), energy-efficient, and works even with normal manufacturing variations. This means it can be built using standard chip processes (CMOS), not exotic parts.
- More stable training: DTMs train more predictably than monolithic EBMs. The ACP keeps the sampler healthy, so gradients are high quality and training progresses smoothly.
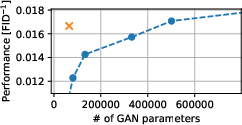
- Hybrid models show promise: Combining a small neural network (to embed data) with a DTM on the CIFAR-10 dataset reached similar quality to a standard GAN, but the neural network was about 10 times smaller. This hints that mixing probabilistic hardware with regular AI can be very efficient.
Implications and Potential Impact
- Greener AI: If AI systems can generate high-quality results using tiny fractions of today’s energy, that would significantly reduce the strain on power grids and lower environmental impact.
- Escaping the “hardware lottery”: AI has grown around GPUs, but that wasn’t guaranteed to be the best path. This work shows a viable alternative hardware-and-algorithm pairing that could be more energy-friendly.
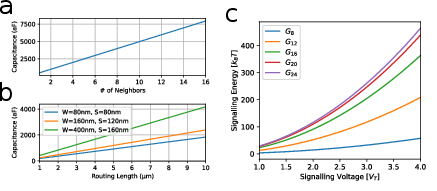
- Scalable and practical: Because this design uses only transistors (standard CMOS), it can be mass-produced and integrated into real-world systems. The authors estimate that a small chip could hold around a million sampling cells—far beyond the sizes used in their experiments—opening the door to stronger models.
- Hybrid thermodynamic-deterministic AI: The future likely isn’t purely probabilistic or purely neural-network-based. The best systems may combine both, choosing the right tool for each part of the job to minimize total energy while hitting the desired accuracy.
- Next steps: Better ways to embed complex data into hardware models, smarter ways to route non-local information, scaling up to larger chains and grids, and improved tools for simulating and co-designing hardware and algorithms. The authors have open-sourced software to help researchers experiment with these ideas today.
In short, this paper suggests a practical path to building AI systems that are both powerful and far more energy-efficient, by combining clever probabilistic modeling (denoising) with hardware built to handle randomness naturally.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of what remains missing, uncertain, or unexplored in the paper, framed as concrete, actionable directions for future research.
- Dataset scope and evaluation breadth:
- Validate DTMs/DTCA on larger, higher-complexity datasets (e.g., ImageNet, high-resolution continuous-valued data) and non-image domains (audio, control, planning) to assess generality beyond binarized Fashion-MNIST.
- Evaluate additional metrics (beyond FID) and tasks (likelihood estimation, conditional generation, downstream utility) to establish broader capability and robustness.
- Data embedding into hardware EBMs:
- Develop principled, hardware-aware embeddings for continuous and categorical variables that avoid naive binarization and reduce visible artifacts (the current grayscale-by-multiple-bits scheme is ad hoc).
- Jointly train embedding networks and DTMs under hardware constraints (locality, quantization, limited connectivity) and compare against the current non-joint setup.
- Quantify the energy/latency overhead of embedding networks in hybrid systems and co-optimize them to maintain net energy advantage.
- Hardware realization beyond RNG demos:
- Build and characterize a full hardware EBM tile (including biasing, interconnect, clocking, memory for weights, and communication fabric), not just the RNG, to validate the device-level energy model and system-level claims.
- Provide measured E_cell, E_comm, E_bias, and E_clock from silicon prototypes and compare to the current physically motivated estimates.
- Scalability and routing feasibility:
- Clarify and correct the die-area scaling estimate (e.g., “∼106 sampling cells in a 6 × 6 µm chip” appears infeasible); supply a realistic PPA (power, performance, area) analysis including wire routing congestion, metal stack usage, and heat dissipation for arrays with ≥106 cells.
- Analyze layout for inter-layer pairwise couplings implementing the forward energy across steps; quantify wire counts, locality guarantees, and place-and-route constraints for large images.
- RNG array behavior and quality:
- Measure spatiotemporal correlations across large arrays of RNG cells under PVT (process, voltage, temperature) variation and switching activity; set acceptable correlation bounds for model accuracy and devise mitigation (e.g., scrambling, calibration).
- Demonstrate faster RNG designs (the paper claims headroom beyond ~100 ns autocorrelation) and quantify the impact of speedups on overall throughput and energy.
- Characterize long-term drift, aging, and environmental sensitivity of the RNG’s voltage-to-probability transfer function and the cost of calibration/compensation.
- Mixing time, throughput, and latency:
- Provide end-to-end sampling latency and throughput projections (samples/second) for realistic model sizes and resolutions, accounting for T steps, K_mix, scheduling (bipartite updates), and parallelism limits.
- Analyze how K_mix scales with dataset complexity and model width/depth, and supply guarantees or empirical bounds for target tasks.
- Training in the loop and stability:
- Demonstrate hardware-in-the-loop or hardware-aware training (including non-idealities: mismatch, quantization, noise) and compare learned parameters and performance to software-trained models.
- Formalize the stability and convergence properties of the Adaptive Correlation Penalty (ACP): derive criteria for setting λ_t, quantify expressivity–mixing trade-offs it induces, and assess sensitivity to the autocorrelation estimator’s noise.
- Define how autocorrelation-based diagnostics (r_yy) can be reliably and efficiently measured on hardware during training and inference.
- Precision, quantization, and calibration:
- Specify and test parameter quantization schemes (bit-widths for J_ij, h_i; analog vs. digital storage) and their impact on model performance and mixing; include calibration methods and their energy/latency overheads.
- Evaluate bias circuit linearity, sigmoid accuracy vs. ideal logistic, temperature dependence, and the effect of non-ideal transfer curves on Gibbs updates and convergence.
- Communication, memory, and control overheads:
- Quantify energy and latency for inter-cell and inter-layer communication at scale, including on-chip network topology choices and contention; validate E_comm with prototypes.
- Include weight loading/programming energy/time (especially if layers are time-multiplexed), on-chip memory choices (SRAM/NVM/analog), and controller overheads in the end-to-end energy model.
- Algorithmic expressivity vs. hardware constraints:
- Explore EBM topologies beyond local, regular grids that better match data correlations while remaining hardware-efficient (e.g., software-defined non-local couplings, routing via sparse long-range interconnect, hierarchical/tileable structures).
- Systematically paper when increasing latent variable count helps or hurts under fixed connectivity and K (as observed in Fig. 6c), and propose architectures that scale expressivity without prohibitive mixing costs.
- Continuous-variable and categorical DTMs:
- Detail and prototype circuits for continuous-variable and categorical EBM layers (not just binary Boltzmann machines), including implementations of the forward energy coupling and samplers, and compare efficiency/accuracy trade-offs.
- Fair and comprehensive energy comparisons:
- Expand energy benchmarking to include training energy (not just inference) for both GPU baselines and the probabilistic system, and include all system overheads (embedding nets, control, calibration).
- Reassess GPU baselines beyond FLOP/J spec (consider memory bandwidth limits, kernel inefficiencies, sparsity, and modern low-precision inference) to ensure apples-to-apples comparisons.
- Hybrid Thermodynamic–Deterministic ML (HTDML) tooling:
- Build a co-design framework (compiler, IR, scheduling/runtime) that partitions computation between probabilistic hardware and deterministic accelerators with energy-aware objectives.
- Demonstrate end-to-end HTDML on nontrivial tasks with principled partitioning strategies and show energy–accuracy Pareto fronts relative to pure-deterministic baselines.
- Large-scale simulation and validation:
- Improve EBM simulation tools to handle sparse, hardware-like structures efficiently and validate them against silicon for correctness and performance; quantify discrepancies between JAX/XLA simulations and on-chip sampling behavior.
- Reliability, robustness, and security:
- Characterize robustness to supply noise, temperature gradients, and device aging at array scale; define guardbands and self-test/calibration strategies.
- Assess failure modes (stuck cells, bias drifts) and their impact on generative quality; develop redundancy or error-tolerant sampling schemes.
- Applications beyond generative modeling:
- Investigate use cases such as planning, control, and inference in structured probabilistic models where DTMs/EBMs might offer stronger advantages, and quantify task-specific energy benefits and constraints.
Practical Applications
Based on the provided content of the research paper, here is an analysis of its practical, real-world applications presented in Markdown format:
Immediate Applications
- Energy-Efficient AI Model Training and Inference
- Industry Use: Can be deployed in data centers to reduce energy consumption associated with AI workloads.
- Sector: Energy, Software
- Assumptions/Dependencies: Requires adaptation of existing infrastructure to accommodate new hardware architecture.
- Probabilistic Hardware for AI
- Academic Use: Can stimulate further research into energy-efficient AI systems.
- Sector: Academia, Energy
- Assumptions/Dependencies: Dependent on successful commercialization of the proposed all-transistor probabilistic computer.
- Denoising Thermodynamic Models (DTMs)
- Daily Life Use: Applied to consumer electronics for energy-efficient AI task handling.
- Sector: Consumer Electronics, Software
- Assumptions/Dependencies: Requires widespread consumer device integration.
Long-Term Applications
- Development of Hybrid Thermodynamic-Deterministic Machine Learning (HTDML) Systems
- Industry Use: Optimization in AI model training by integrating probabilistic computing with traditional determinist models.
- Sector: AI, Robotics
- Assumptions/Dependencies: Needs significant research into embedding procedures and real-world dataset applications.
- Scalable Energy-Based Model (EBM) Enhanced AI Systems
- Policy Use: Influence national strategies for sustainable technology and infrastructure.
- Sector: Energy Policy, Sustainability
- Assumptions/Dependencies: Dependent on policy shifts towards sustainable technology investment.
- Integration of Probabilistic Computing in Mainstream AI Systems
- Industry Use: Can influence the design of new AI systems that require less energy and provide higher efficiency.
- Sector: AI, Hardware Design
- Assumptions/Dependencies: Significant developmental improvements in probabilistic computing technology and acceptance in the industry.
- Acceleration of Research in Energy-Efficient Networks
- Academic Use: Influences curriculum and research in electronic engineering and computer science programs.
- Sector: Education, Research
- Assumptions/Dependencies: Requires broad academic interest and funding for exploratory studies.
These applications highlight potential tools, products, or workflows that could emerge from the research findings, focusing on energy efficiency and AI advancements, with a specific emphasis on how they can be deployed or researched further in various sectors.
Glossary
- Adaptive Correlation Penalty (ACP): A closed-loop regularization strategy that adjusts the strength of a correlation penalty per layer to keep sampling tractable during training. "We use an Adaptive Correlation Penalty (ACP) to set the as large as necessary to keep sampling tractable for each layer."
- Autocorrelation function: A measure of the similarity of a stochastic process with a delayed version of itself, used here to assess mixing quality and RNG dynamics. "The autocorrelation function of the RNG at the unbiased point ()."
- Autoregressive LLM: A model that generates sequences by predicting the next token conditioned on previous tokens. "Existing AI systems based on autoregressive LLMs are valuable tools in white-collar fields~\cite{alphacode, gptbar, nori2023capabilities, work_1, work_2, work_3}"
- Bernoulli sampling circuit: A hardware element that outputs binary random variables with a controllable probability. "A device will consist of a regular grid of Bernoulli sampling circuits, where each sampling circuit implements the Gibbs sampling update for a single variable ."
- Bipartite (two-colorable): A graph structure whose nodes can be partitioned into two sets with edges only between sets, enabling parallel block updates. "Due to our chosen connectivity patterns, our Boltzmann machines are bipartite (two-colorable)."
- Boltzmann distribution: A probability distribution proportional to the exponential of negative energy, central to EBMs and physical sampling. "to efficiently and quickly produce samples from a Boltzmann distribution~\cite{singh2024cmos}."
- Boltzmann machine: An undirected energy-based model with binary variables and pairwise couplings, sampled via Gibbs updates. "The DTM that produced the results shown in Fig.~\ref{fig:perf} used Boltzmann machine EBMs."
- CMOS: Complementary metal–oxide–semiconductor technology used for fabricating integrated circuits. "our new architecture can be implemented at scale using present-day CMOS processes"
- Compute-in-memory: An architectural approach that performs computation within memory arrays to reduce data movement. "Active efforts include mixedâsignal computeâinâmemory accelerators~\cite{ibm_analog}, photonic neural networks~\cite{mit_photonic}, and neuromorphic processors that emulate biological spiking~\cite{spinn2, lohi2}."
- Denoising diffusion model: A generative model that learns to reverse a gradual noising process to synthesize data. "Denoising diffusion models were explicitly designed to sidestep the MET by gradually building complexity through a series of simple, easy-to-sample probabilistic transformations~\cite{diff_orig}."
- Denoising Thermodynamic Computer Architecture (DTCA): A hardware architecture that chains EBMs to implement efficient denoising-based generative modeling. "The Denoising Thermodynamic Computer Architecture (DTCA) tightly integrates DTMs into probabilistic hardware, allowing for the highly efficient implementation of EBM-aided diffusion models."
- Denoising Thermodynamic Model (DTM): A model that composes multiple EBMs to reverse a forward noising process, avoiding the EBM mixing-expressivity tradeoff. "we introduce a new probabilistic computer architecture that runs Denoising Thermodynamic Models (DTMs) instead of monolithic EBMs."
- Energy-Based Model (EBM): A model class that assigns energies to configurations, defining probabilities via a Boltzmann distribution. "Energy-Based Models (EBMs) are a well-established model class in contemporary deep learning and have been competitive with the state of the art in tasks like image generation and robotic path planning~\cite{song2019generative, janner2022planning}."
- Fréchet Inception Distance (FID): A metric for evaluating the quality of generated images by comparing feature distributions. "evaluated with Fréchet Inception Distance (FID)~\cite{heusel2017ttur}."
- Generative Adversarial Network (GAN): A generative framework with a generator and discriminator trained in opposition. "VAE~\cite{kingma2022autoencodingvariationalbayes} and GAN~\cite{goodfellow2014generative}"
- Gibbs sampling: A Markov chain Monte Carlo method that iteratively samples each variable conditioned on the others. "or may be orchestrated using an algorithm like Gibbs sampling~\cite{niazi2024training, kerem_factorization, kerem_learning, kerem_sparse}."
- Hybrid thermodynamic-deterministic machine learning (HTDML): Systems that combine probabilistic hardware with deterministic accelerators to optimize energy and performance. "a larger hybrid thermodynamic-deterministic machine learning (HTDML) system."
- Ising model: A spin system from statistical physics equivalent to a binary Boltzmann machine. "Boltzmann machines, also known as Ising models in physics, use binary random variables and are the simplest type of discrete-variable EBM."
- Itô diffusion: A stochastic differential equation-driven process used as a forward noising process in continuous spaces. "the It^{o} diffusion,"
- Kullback-Leibler (KL) divergence: A measure of discrepancy between two probability distributions used for training denoising models. "minimize the Kullback-Leibler (KL) divergence between the joint distributions and ,"
- Latent variable: An unobserved variable introduced to increase model expressivity or structure. "To maximally leverage probabilistic hardware for EBM sampling, DTMs generalize Eq.~\eqref{eq:ebm_cond} by introducing latent variables :"
- Markov chain: A sequence of random variables where the next state depends only on the current state. "The forward process is given by the Markov chain"
- Markov jump process: A discrete-state stochastic process with transitions occurring at random times, used as a discrete forward process. "and a Markov jump process in the discrete case."
- Mixing time: The number of iterations required for a sampler to approximate the target distribution well. "mixing time (the amount of computational effort needed to draw independent samples from the MEBM's distribution)"
- Mixing-expressivity tradeoff (MET): The phenomenon where more expressive monolithic EBMs are harder to sample (mix) efficiently. "The mixing-expressivity tradeoff (MET) summarizes this issue with existing probabilistic computer architectures, reflecting the fact that modeling performance and sampling hardness are coupled for MEBMs."
- Monte Carlo estimator: An estimator that uses random sampling to approximate expectations or gradients. "the standard Monte-Carlo estimator for the gradients of EBMs"
- Neuromorphic processor: Hardware that emulates neural spiking to perform brain-inspired computation. "neuromorphic processors that emulate biological spiking~\cite{spinn2, lohi2}."
- Photonic neural network: An optical computing approach to implement neural networks using light. "photonic neural networks~\cite{mit_photonic}"
- Process corners: Foundry-defined extremes of device parameters used to assess sensitivity to manufacturing variations. "Each color represents a different process corner, each for which realizations of the RNG were simulated."
- Process development kit (PDK): A foundry-provided model and rule set for simulating and designing circuits in a given process. "we use this process development kit (PDK) to study the speed and energy consumption of our RNG"
- Random-number generator (RNG): A circuit that produces random bits, here with programmable bias and fast dynamics. "magnetic tunnel junctions as sources of intense thermal noise for random-number generation (RNG)~\cite{lee2025correlation, horodynski2025stochastic, kerem_learning}."
- Shot noise: Intrinsic electronic noise arising from discrete charge carriers, leveraged for randomness. "we leveraged the shot-noise dynamics of subthreshold transistors~\cite{freitas2025} to build an RNG"
- Sigmoid function: A smooth S-shaped function mapping inputs to probabilities in (0,1). "The relationship between and the input voltage is well-approximated by a sigmoid function."
- Stationary distribution: A distribution invariant under the dynamics of a Markov process. "The forward process is typically chosen such that it has a unique stationary distribution , which takes a simple form (e.g., Gaussian or uniform)."
- Stochastic differential equation (SDE): A differential equation with a stochastic term modeling continuous-time randomness. "This conversion into noise is achieved through a stochastic differential equation in the continuous-variable case"
- Subthreshold transistor: A transistor operated in weak inversion where current is dominated by exponential behavior and shot noise. "Our RNG leverages the stochastic dynamics of subthreshold transistor networks, which we have recently studied in detail in Ref.~\cite{freitas2025}."
- Thermodynamic computing: A computing approach that exploits stochastic, energy-based dynamics to sample distributions efficiently. "Using probabilistic hardware to accelerate EBMs falls under the broad umbrella of thermodynamic computing~\cite{conte2019thermodynamic}."
- Total correlation penalty: A regularizer that penalizes dependencies by comparing a joint distribution to the product of its marginals. "and is a form of total correlation penalty~\cite{chen2018isolating}."
- Transition kernel: The conditional probability that defines how a stochastic process evolves from one state to another. "The transition kernel for a random process defines how the probability distribution evolves in time,"
- Variational Autoencoder (VAE): A generative model trained via variational inference with an encoder-decoder structure. "VAE~\cite{kingma2022autoencodingvariationalbayes}"
- Wiener process: A continuous-time Gaussian process with independent increments, modeling Brownian motion. "where is a length vector representing the state variable at time , is a constant, and is a length vector of independent Wiener processes."
Collections
Sign up for free to add this paper to one or more collections.