ParaRNN: Unlocking Parallel Training of Nonlinear RNNs for Large Language Models (2510.21450v1)
Abstract: Recurrent Neural Networks (RNNs) laid the foundation for sequence modeling, but their intrinsic sequential nature restricts parallel computation, creating a fundamental barrier to scaling. This has led to the dominance of parallelizable architectures like Transformers and, more recently, State Space Models (SSMs). While SSMs achieve efficient parallelization through structured linear recurrences, this linearity constraint limits their expressive power and precludes modeling complex, nonlinear sequence-wise dependencies. To address this, we present ParaRNN, a framework that breaks the sequence-parallelization barrier for nonlinear RNNs. Building on prior work, we cast the sequence of nonlinear recurrence relationships as a single system of equations, which we solve in parallel using Newton's iterations combined with custom parallel reductions. Our implementation achieves speedups of up to 665x over naive sequential application, allowing training nonlinear RNNs at unprecedented scales. To showcase this, we apply ParaRNN to adaptations of LSTM and GRU architectures, successfully training models of 7B parameters that attain perplexity comparable to similarly-sized Transformers and Mamba2 architectures. To accelerate research in efficient sequence modeling, we release the ParaRNN codebase as an open-source framework for automatic training-parallelization of nonlinear RNNs, enabling researchers and practitioners to explore new nonlinear RNN models at scale.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces ParaRNN, a new way to train a type of AI model called a Recurrent Neural Network (RNN) much faster by doing many steps at the same time. RNNs are good at handling sequences (like sentences or time series), but they usually have to process one item after another, which slows training down. ParaRNN breaks this “one-by-one” barrier, making even complex, nonlinear RNNs train in parallel like Transformers and modern State Space Models (SSMs).
Objectives and Research Questions
The paper sets out to answer a simple question: can we make nonlinear RNNs train as fast and big as today’s best models, without losing their strengths?
To do that, the authors aim to:
- Unlock parallel training for nonlinear RNNs, which traditionally run step-by-step.
- Scale RNNs to billions of parameters, similar to LLMs.
- Show that these RNNs can match the quality of Transformers and Mamba/Mamba2 on language tasks.
- Release a practical, open-source toolkit so others can build and experiment with parallelized RNNs.
Methods and Approach (Explained Simply)
Think of an RNN like a line of dominoes: each domino (word or token) falls after the previous one. That makes training slow because you can’t push many dominoes at once. The authors change the game so you can solve the whole line together.
Here’s how they do it:
- Turning the sequence into one big puzzle:
- Normally, an RNN updates its hidden state one step at a time. Instead, the authors rewrite the whole sequence as one big system of equations—like a giant puzzle that represents all steps at once.
- Using Newton’s method (guess, check, and fix):
- Newton’s method is a classic approach in math where you start with a guess, check how far off it is, and adjust to improve. You repeat this a few times until you get a good answer.
- In this context, each “fix” step becomes a simpler, linear problem that’s easier to solve fast.
- Solving the simpler problem in parallel:
- The linear problem has a special ladder-like structure (called “block bi-diagonal”). This structure makes it perfect for a technique similar to computing running totals in parallel (often called a “prefix scan” or “parallel reduction”).
- Imagine a team passing partial results forward in smart batches, instead of one person doing everything alone. That lets many parts be handled at once.
- Adapting GRU and LSTM to be parallel-friendly:
- GRU and LSTM are popular RNN “cells.” To make them efficient in this new setup, the authors slightly change them so certain math pieces (called “Jacobians,” which describe how outputs change when inputs change) become simple and “diagonal.” That means each hidden unit can be updated independently, which is great for parallel work.
- Don’t worry—mixing of features still happens in other parts of the model (like MLP layers), so the model remains expressive.
- High-performance implementation:
- They provide multiple versions: a simple PyTorch version for prototyping, a fast CUDA version, and a fully fused CUDA version (the fastest), where everything runs inside a single optimized GPU kernel.
Main Findings and Why They Matter
- Big speedups:
- ParaRNN achieves up to 665× speedup compared to naive, step-by-step RNN training. That’s a huge jump, turning RNNs into practical options again.
- Scales to large models:
- They successfully trained adapted GRU and LSTM models with around 7 billion parameters, which is LLM territory.
- Competitive quality:
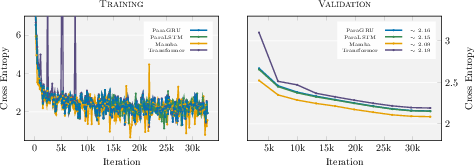
- These RNNs reached perplexity (a common language modeling score) comparable to similarly sized Transformers and Mamba2.
- On downstream tasks (like commonsense reasoning and multiple-choice benchmarks), Mamba2 is strongest, but ParaGRU and ParaLSTM are close and often ahead of regular Transformers trained under similar conditions.
- Fast inference:
- Generating text (inference) is fast and does not slow down as sequences get longer. Measured throughput was similar to or better than Mamba and faster than Transformers in the tested setup.
- Nonlinearity helps:
- On small “stress tests” designed to check reasoning skills (like the Parity task and k-hop reasoning), nonlinear RNNs (ParaGRU/ParaLSTM) solved tasks that linear SSMs struggle with. This shows the value of keeping nonlinear parts in sequence models.
Implications and Impact
ParaRNN changes the story for RNNs:
- It proves that nonlinear RNNs can be trained in parallel at scale, removing their biggest practical barrier.
- It offers a real alternative to Transformers and SSMs, especially for cases where fast inference and lower memory use matter.
- It encourages researchers to explore new nonlinear RNN designs without being blocked by training speed.
- The open-source framework lets the community build and test new ideas quickly, potentially leading to more efficient and expressive LLMs in the future.
In short, ParaRNN makes classic RNNs competitive again by letting them train like modern models—fast, large, and powerful—while keeping their unique strengths.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of concrete gaps and open questions that the paper leaves unresolved and that future work could directly address.
- Convergence guarantees in O(1) Newton steps
- No theoretical conditions are provided that ensure convergence of Newton’s method in a constant number of iterations for GRU/LSTM variants used here; derive sufficient conditions (e.g., contractivity bounds, Jacobian spectral constraints) under which 2–3 iterations provably suffice across training.
- Newton solver stabilization and adaptivity
- The paper uses a fixed iteration budget (≈3); investigate adaptive stopping criteria, damping/line search, or trust-region strategies that balance accuracy and throughput, and characterize their effects on training stability and final quality.
- Gradient correctness under inexact forward solves
- When the forward fixed point is only approximated (few Newton steps), the backward pass assumes exact recurrence gradients; quantify the bias this introduces, compare against implicit differentiation or differentiating through the solver, and assess impact on optimization and generalization.
- Numerical conditioning and precision
- Products of Jacobians across long sequences can be ill-conditioned; evaluate conditioning, overflow/underflow risks in mixed precision (FP16/BF16), and develop preconditioning, rescaling, or normalization techniques that improve numerical robustness.
- Memory and compute overhead of Jacobian assembly
- Autograd-based Jacobian assembly is a bottleneck; profile and reduce its overhead, especially for longer sequences and larger hidden sizes, and compare explicit analytic Jacobians vs autograd in accuracy, memory, and speed.
- Expressivity loss from diagonal (or block-diagonal) Jacobians
- The enforced diagonal structure removes intra-state mixing inside the RNN cell; quantify the expressivity trade-off and recoverability via surrounding MLPs, and test alternative structures (low-rank, banded, grouped block-diagonal, Householder/orthogonal factors) that preserve parallelism while increasing capacity.
- Ablations on Jacobian structure vs model quality
- Provide systematic ablations isolating the effect of diagonalization (and peephole simplifications) on perplexity, in-context abilities, and long-range reasoning, holding parameter counts and training budgets fixed.
- Scaling to longer contexts
- Performance and stability for very long contexts (e.g., 32k–128k tokens) are not reported; evaluate wall-time, memory, kernel efficiency and quality, and identify algorithmic limits or needed changes (e.g., multi-stage scans, tiling).
- End-to-end training throughput and energy
- Most timings emphasize kernels/forward; report end-to-end training throughput (including backward, optimizer, dataloader), GPU memory footprint, and energy consumption vs Transformers and SSMs for fair compute-quality trade-offs.
- Backward-pass profiling and optimization
- The backward pass is described but not profiled in depth; measure and optimize its time/memory contribution, and test fused backward kernels analogous to the fused forward.
- Robustness across hardware and software stacks
- CUDA-only implementation leaves portability uncertain; evaluate on different GPUs (architectures, memory hierarchies), multi-GPU systems, ROCm, and TPUs, and quantify portability, tuning needs, and performance variance.
- Distributed training at scale
- How sequence-parallel time solve interacts with data/tensor/pipeline parallelism is untested; design and benchmark scalable parallelization strategies (e.g., sharding along sequence vs batch vs model) and synchronization costs.
- Initialization and warm-start strategies for Newton
- Investigate using warm starts from previous batches/chunks or lightweight sequential previews to reduce iterations, and quantify speed/quality benefits and potential biases.
- Error control and solver–optimizer interaction
- Study how the residual tolerance or iteration budget should adapt across training, learning-rate schedules, and optimizer states (e.g., AdamW vs Adafactor) to maintain stability.
- Theoretical links to contraction/monotonicity in gated RNNs
- Establish bounds (e.g., on gate ranges, weight norms) that enforce global or local contraction, ensuring solver convergence and stable training dynamics for the proposed cells.
- Alternative nonlinear solves
- Compare Newton against Anderson acceleration, quasi-Newton (LBFGS), Gauss–Newton, or learned solvers; evaluate iteration count, stability, and kernel efficiency trade-offs.
- Solver preconditioning and layout
- Explore preconditioners tailored to the bidiagonal block structure and to diagonal/block-diagonal Jacobians that reduce iteration count or improve mixed-precision stability.
- Interaction with normalization and gating
- Analyze how normalization layers and gate saturations affect Jacobian spectra and solver convergence; propose architectural tweaks (e.g., gate temperature, norm constraints) that improve conditioning.
- Task breadth and evaluation coverage
- Beyond perplexity and a subset of lm-eval-harness tasks, assess instruction following, reasoning (BBH, GSM8K), safety, multilingual, and retrieval-heavy tasks to map where nonlinear RNNs excel or lag.
- Long-range generalization and in-context learning
- Quantify in-context learning, compositional generalization, and retrieval behavior at scale relative to SSMs and Transformers; connect to synthetic task strengths.
- Scaling beyond 7B and data budgets
- Test larger models (≥13B) and varied data scales; report Chinchilla-style compute-optimal curves and whether ParaRNN maintains parity or improves with scale.
- Compatibility with advanced training regimes
- Evaluate fine-tuning (SFT), preference optimization (DPO/RLHF), and post-training alignment workflows; identify any solver-related instabilities or throughput regressions.
- Hybrid architectures
- Investigate mixing attention and ParaRNN layers (e.g., sparse attention every N blocks) to recover global interactions while retaining parallel RNN efficiency; quantify trade-offs.
- Structured sparsity and MoE integration
- Explore combining ParaRNN with MoE and structured sparsity to increase capacity without sacrificing solver efficiency, and address how expert routing interacts with solver batching.
- Checkpointing and memory–compute trade-offs
- Develop checkpointing strategies tailored to Newton and reductions to reduce peak memory on long sequences with minimal recompute overhead.
- Reproducibility and code accessibility
- The paper claims open-source release, but the provided URL appears to be an internal repository; clarify public availability, provide versioned releases and scripts for reproducing all results.
- Fair baselines against optimized sequential RNNs
- The claimed 665× speedup is versus naïve sequential baselines; compare against state-of-the-art fused/optimized sequential RNN implementations to establish realistic speedups.
- Generality beyond language
- Validate ParaRNN in speech, audio, time-series, and video (where RNNs/SSMs are strong) to test solver robustness and efficiency across modalities and signal statistics.
- Safety and failure-mode analysis
- Characterize failure modes specific to solver convergence (e.g., rare divergence, sensitivity to sequence content), and propose monitoring/mitigation during training and inference.
Practical Applications
Immediate Applications
Below are concrete, deployable-now applications that leverage ParaRNN’s findings: Newton-based sequence parallelization for nonlinear RNNs, CUDA-optimized parallel reductions for block bi-diagonal solves, and LSTM/GRU adaptations (ParaLSTM/ParaGRU) with diagonal Jacobians enabling training and inference at scale.
- Faster, cheaper LLM training with nonlinear RNNs (software, cloud/AI infra)
- What: Replace attention or linear SSM blocks with ParaGRU/ParaLSTM to train 0.4B–7B models with Transformer/Mamba-like training speed and RNN-like inference efficiency.
- Tools/workflows: ParaRNN PyTorch+CUDA library; use “CUDA-Accelerated” or “Fully-fused” implementations for production; drop-in model blocks in existing PyTorch training stacks; mixed-precision and sequence-parallel data loaders.
- Assumptions/dependencies: CUDA GPUs; short O(1) Newton convergence (empirically ~3 iterations); diagonal/block-diagonal Jacobians; PyTorch autograd compatibility; library availability.
- On-device, low-latency assistants and keyboards (mobile, edge AI; daily life)
- What: Deploy ParaGRU/ParaLSTM for predictive typing, autocomplete, and small personal assistants with constant-time next-token generation and reduced memory.
- Tools/products: Mobile inference runtimes (Core ML, Metal, NNAPI) with RNN kernels; distilled ParaRNN models; caching-friendly streaming.
- Assumptions/dependencies: Efficient mobile kernels; quantization-aware training; conversion tooling from PyTorch; memory limits.
- Streaming speech and audio understanding with better latency (media, accessibility; healthcare)
- What: ASR, voice activity detection, speaker diarization, and keyword spotting with RNN-based streaming pipelines that don’t slow with sequence length.
- Tools/workflows: ParaRNN encoder blocks in streaming speech models; real-time batching; on-device inference.
- Assumptions/dependencies: Stable Newton convergence on audio RNNs; optimized kernels for long audio frames; modest mixing via MLP layers to offset diagonal state.
- Real-time anomaly detection and log analytics (cybersecurity, DevOps, finance)
- What: Use ParaRNN sequence models for continuous log streams, fraud detection, and high-frequency market signals where low-latency updates are critical.
- Tools/workflows: Replace attention blocks in online analytics; serve via Triton/TensorRT pipelines calling CUDA-fused kernels; concept drift monitoring.
- Assumptions/dependencies: GPU/edge accelerator access for fused kernels; streaming ingestion; reliable O(1)-iteration Newton solves.
- Time-series forecasting and control in IoT/industry (manufacturing, energy, robotics)
- What: Deploy RNNs for forecasting (load, demand, sensor signals) and control loops (robotics, HVAC) where constant-latency inference matters.
- Tools/workflows: ParaGRU/ParaLSTM backbones for multivariate time-series; rolling-window training; on-device deployment in gateways/PLCs.
- Assumptions/dependencies: Diagonal-Jacobian-compatible cell design; calibration for long horizons; limited compute on edge devices.
- Academic exploration of nonlinear RNN design space at scale (academia)
- What: Rapidly prototype new nonlinear recurrent cells and train them at LLM scales without sequential bottlenecks.
- Tools/workflows: ParaRNN “Pure PyTorch” for prototyping; CUDA solver for performance baselines; ablation of Jacobian structures; synthetic task suites (MQAR, k-hop, Parity) for expressivity.
- Assumptions/dependencies: Access to GPUs; understanding of Jacobian structure to keep compute O(dh); unit tests for convergence and stability.
- Hybrid RNN-SSM systems in production (software, ML platforms)
- What: Combine SSM layers for efficient linear memory and ParaRNN layers for nonlinear capacity in the same model stack.
- Tools/workflows: Model configs that interleave Mamba-like layers and ParaGRU/ParaLSTM; shared scan/reduction runtime; standard training loops.
- Assumptions/dependencies: Scheduling of multiple kernel types; memory bandwidth planning; monitoring convergence across heterogeneous blocks.
- Cost and energy reduction in training (policy, sustainability; cloud ops)
- What: Swap attention with ParaRNN blocks to reduce wall-clock time and memory, yielding lower energy per trained token.
- Tools/workflows: Emissions tracking (CodeCarbon, internal meters); cluster schedulers that favor fused ParaRNN jobs; carbon reporting in ML platforms.
- Assumptions/dependencies: Comparable or better throughput validated on internal datasets; accurate energy metering; organizational willingness to adopt RNN-based stacks.
- Curriculum/testing for sequence expressivity beyond linear SSMs (education, academia)
- What: Course modules and lab assignments that contrast linear SSMs vs nonlinear RNNs using ParaRNN on retrieval, state-tracking, and parity tasks.
- Tools/workflows: Open-source notebooks; standardized synthetic benchmarks; unit tests for Newton iteration behavior.
- Assumptions/dependencies: Stable release of the library; CI for GPU-enabled assignments.
Long-Term Applications
These depend on further research, scale-up, kernel/compiler integration, or ecosystem support.
- New families of expressive, parallel nonlinear RNNs (academia, software)
- What: Architectures beyond diagonal-Jacobian ParaGRU/ParaLSTM (e.g., low-rank/structured Jacobians, learned preconditioners, selective updates) with retained parallelism.
- Tools/workflows: Auto-derivation of Jacobian structure; regularizers enforcing sparsity/structure; ParaRNN extension APIs.
- Assumptions/dependencies: Theoretical advances on convergence and stability; kernel support for broader structures; training recipes.
- Hardware-software co-design for Newton + parallel-scan workloads (semiconductors, cloud)
- What: Accelerators and GPU features optimized for block bi-diagonal solves, warp-level scans, and fused Jacobian assembly.
- Tools/products: Firmware/primitives for structured scans; compiler passes; memory hierarchies prioritizing scan/tri-diagonal patterns.
- Assumptions/dependencies: Vendor adoption; benchmark-driven justification vs attention kernels; standardization of APIs.
- Compiler-level integration and graph fusions (ML compilers, platforms)
- What: TorchInductor/TVM/XLA passes that auto-fuse recurrence, Jacobian assembly, and parallel reduction across model graphs.
- Tools/workflows: Pattern-matching of Markovian recurrences; AOT autograd for Jacobians; layout transformations reducing memory traffic.
- Assumptions/dependencies: Stable IR support; correctness guarantees; broad model coverage.
- Large-scale (>70B) nonlinear RNN LLMs with long-context training (cloud AI, enterprise)
- What: Train frontier-scale RNN LLMs with efficient parallelized training and inference memory advantages for long contexts and streaming use.
- Tools/workflows: Mixture-of-Experts with ParaRNN experts; KV-free serving; chunked context accumulation; retrieval-augmented pipelines.
- Assumptions/dependencies: Demonstrated scaling laws; scheduler support; distributed Newton/scan algorithms; memory-optimized kernels.
- Multimodal streaming AI (vision, audio, sensors) with constant-latency inference (media, robotics, automotive)
- What: Video-language, sensor fusion, and AV perception pipelines where inference cost doesn’t grow with sequence length.
- Tools/workflows: ParaRNN encoders for event streams; online fusion blocks; uncertainty-aware controllers.
- Assumptions/dependencies: Extensions of ParaRNN to multimodal recurrences; robust convergence in high-dimensional streams; safety certification in control.
- Federated and privacy-preserving on-device modeling (healthcare, finance, public sector)
- What: Personal RNN models trained locally or federated (EHR time-series, personal assistants) with better energy and privacy profiles than attention-heavy stacks.
- Tools/workflows: Federated averaging with ParaRNN; DP-SGD; client-side quantization; secure aggregation.
- Assumptions/dependencies: Efficient mobile/server kernels; training stability under client heterogeneity; regulatory acceptance.
- Energy-aware AI policies and standards (policy, sustainability)
- What: Incentives and procurement guidelines favoring efficient sequence models; reporting standards that recognize parallel nonlinear RNNs’ energy profile.
- Tools/workflows: Benchmarks for Joules-per-token; model cards with efficiency metrics; green AI certifications.
- Assumptions/dependencies: Community consensus on metrics; third-party audits; reproducible energy measurements.
- Tooling for automated Jacobian-structure discovery (software, research tooling)
- What: Automated search/constraints that produce RNN cells with parallel-scan-friendly Jacobians (diagonal, block-diagonal, banded, low-rank).
- Tools/workflows: NAS with structure penalties; symbolic differentiation libraries emitting structured kernels; autotuners for scan strategies.
- Assumptions/dependencies: Reliable structure-enforcing training; compiler backend support; generalization beyond language.
- Robust training under extreme sequence lengths and noisy dynamics (academia, high-stakes systems)
- What: Stabilized Newton methods (line search, damping, trust regions) and learned preconditioners enabling ParaRNN in chaotic or very long sequences (finance, grids).
- Tools/workflows: Adaptive iteration control; convergence monitors; fallback-to-sequential heuristics; hybrid Gauss–Newton schemes.
- Assumptions/dependencies: Theoretical guarantees for convergence rates; overhead control keeping O(1) iterations on average.
- Standardized ParaRNN backends in serving stacks (ML ops)
- What: First-class ParaRNN backends in Triton, ONNX Runtime, TensorRT, and inference gateways for easy deployment.
- Tools/workflows: Graph exporters; kernel registries; A/B testing harnesses for RNN vs attention latency/cost.
- Assumptions/dependencies: Ecosystem integration; maintenance of CUDA kernels across hardware generations; ONNX op standardization.
Notes on Global Assumptions/Dependencies
- Newton convergence in small O(1) iterations is necessary for speed; empirical validation per new cell/domain is recommended.
- Structured Jacobians (diagonal or small block-diagonal) are critical to keep memory O(dh) and multiplication O(dh); feature mixing must be provided by surrounding layers (e.g., MLPs).
- Current peak performance targets CUDA GPUs; portability to other backends (ROCm, Metal, NPUs) requires kernel reimplementation.
- ParaRNN assumes Markovian recurrences; non-Markov models may need reformulations.
- Library availability and licensing must permit commercial use; integration into existing pipelines (PyTorch versions, autograd) is required.
Glossary
- All-at-once system: A formulation that aggregates a sequence of coupled equations into a single system solved collectively. "automatically assembling the resulting all-at-once system."
- Autograd: Automatic differentiation mechanism (e.g., in PyTorch) that computes gradients and Jacobians from computational graphs. "it leverages autograd to assemble the Jacobians required in \cref{eqn::newton_it}"
- Autoregressive: A generation process where each new output token depends on previously generated tokens. "for RNNs the time necessary to autoregressively produce the next token in the output does not grow with sequence length."
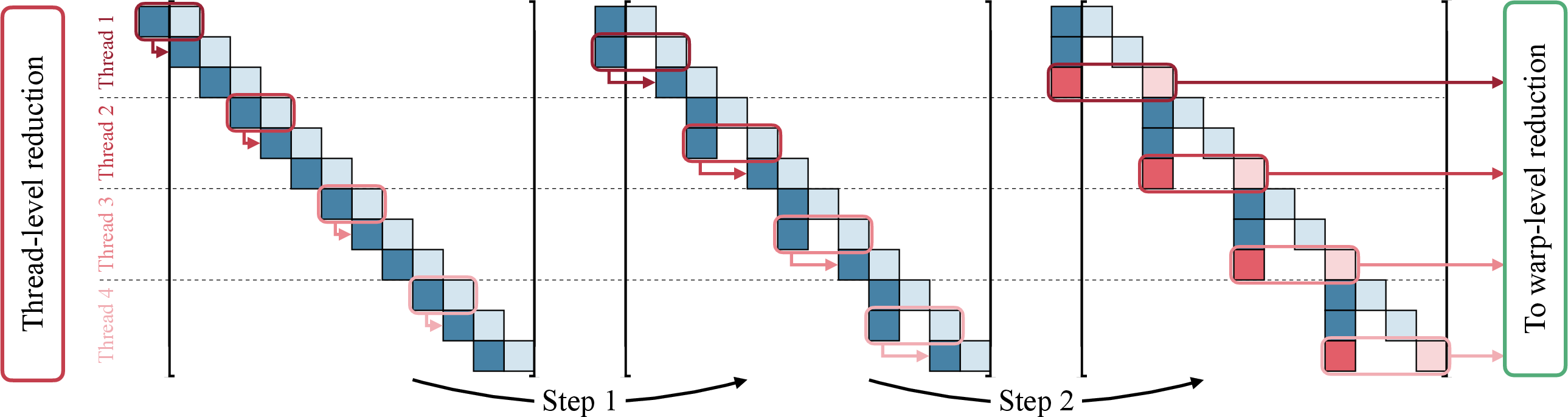
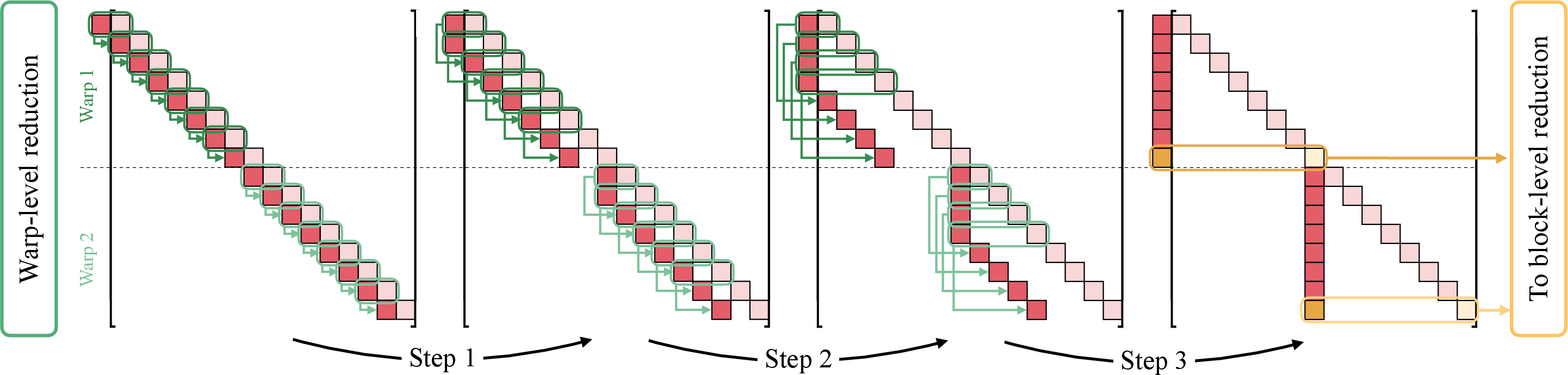
- Block bi-diagonal: A sparse matrix structure with nonzero blocks only on the main diagonal and the first sub/super-diagonals. "the resulting linearized system obeys a specific block bi-diagonal structure"
- Block-diagonal: A matrix composed of square diagonal blocks with zeros elsewhere, enabling independent block-wise operations. "specialized for Jacobians with diagonal or -block-diagonal structure as in \cref{eqn::GRU_LSTM_jac}."
- Causal convolution: A convolution where outputs at time t only depend on inputs at time ≤ t, preserving sequence causality. "including also the causal convolution and gated residual layers from Mamba"
- Chinchilla-optimal scaling: A training regime balancing model size and data quantity to optimize compute efficiency and performance. "and follow Chinchilla-optimal~\citep{hoffmann2022trainingcomputeoptimallargelanguage} scaling for their training setup"
- CUDA kernel: A GPU-executed function written for CUDA to accelerate parallel computations. "A performant implementation featuring a custom CUDA kernel for the parallel reduction solver"
- Diagonal approximation: Approximating a matrix by keeping only its diagonal, reducing memory and compute cost. "where a diagonal approximation of the full RNN Jacobian is employed for computational efficiency"
- Forward substitution: A method to solve lower-triangular linear systems sequentially from the first variable onward. "its solution could be explicitly recovered by forward substitution"
- Fully-fused CUDA kernel: A single CUDA kernel that combines multiple computation steps to minimize memory traffic and launch overhead. "Fully-fused Our most performant implementation where the whole Newton routine, including iterative Jacobian assembly and parallel solution, is fused within a single CUDA kernel."
- Gauss-Seidel: An iterative solver for linear systems that updates variables in sequence using the latest values. "Jacobi and Gauss-Seidel solvers are applied to accelerate ResNets applications"
- Gated residual layers: Layers that modulate residual connections with gates to control information flow. "including also the causal convolution and gated residual layers from Mamba"
- Jacobian: The matrix of first-order partial derivatives of a vector-valued function, capturing local linear behavior. "denotes the Jacobian of the recurrence step \cref{eqn::rnn_seq} with respect to the hidden state "
- Jacobi: An iterative linear solver updating all variables using previous-iteration values, often parallelizable. "Jacobi and Gauss-Seidel solvers are applied to accelerate ResNets applications"
- Mamba: A modern linear state space model architecture optimized for parallel sequence processing. "Mamba and Mamba2 \citep{mamba,mamba2}"
- Markovian: A property where the next state depends only on the current state (and input), not the full history. "In light of the Markovian nature of classical RNNs"
- Newton's method: An iterative root-finding technique that solves nonlinear systems via successive linearizations. "To solve this system, we rely on Newton's method"
- Parallel reduction: A parallel algorithm that combines elements (e.g., via sums/products) using associative operations in logarithmic time. "using custom high-performance implementations of parallel reduction operations."
- Parallel scan: A parallel algorithm computing all prefix aggregates of a sequence, also known as parallel reduction/prefix sum. "prefix sum (also known as parallel reduction, or parallel scan \citep{parallelscanOG,parallelscan})"
- Peephole connections: LSTM connections where gates directly access the cell state, enhancing temporal control. "For the latter, we consider its variant equipped with peephole connections and combining input and forget gates"
- Perplexity: A language-modeling metric measuring how well a model predicts a sample; lower is better. "attain perplexity comparable to similarly-sized Transformers and Mamba2 architectures."
- Picard iterations: Fixed-point iterations used to solve equations or differential systems, applicable to parallelizing sequential steps. "Picard iterations are used to parallelize denoising steps in Diffusion."
- Prefix sum: The sequence of cumulative aggregates over input elements, foundational for parallel scan algorithms. "prefix sum (also known as parallel reduction, or parallel scan \citep{parallelscanOG,parallelscan})"
- Quasi-Newton method: An optimization/solver technique approximating the Newton step (e.g., with simplified Jacobians/Hessians). "the authors consider the use of a quasi-Newton method"
- State Space Models (SSMs): Sequence models defined by linear state transitions and inputs, enabling parallel training. "This has led to the dominance of parallelizable architectures like Transformers and, more recently, State Space Models (SSMs)."
- Warp (GPU): A group of threads that execute instructions in lockstep on NVIDIA GPUs, enabling efficient parallelism. "thread, warp, block and device, see \cite{cuda2025}"
Collections
Sign up for free to add this paper to one or more collections.