Self-diffusion for Solving Inverse Problems (2510.21417v1)

Abstract: We propose self-diffusion, a novel framework for solving inverse problems without relying on pretrained generative models. Traditional diffusion-based approaches require training a model on a clean dataset to learn to reverse the forward noising process. This model is then used to sample clean solutions -- corresponding to posterior sampling from a Bayesian perspective -- that are consistent with the observed data under a specific task. In contrast, self-diffusion introduces a self-contained iterative process that alternates between noising and denoising steps to progressively refine its estimate of the solution. At each step of self-diffusion, noise is added to the current estimate, and a self-denoiser, which is a single untrained convolutional network randomly initialized from scratch, is continuously trained for certain iterations via a data fidelity loss to predict the solution from the noisy estimate. Essentially, self-diffusion exploits the spectral bias of neural networks and modulates it through a scheduled noise process. Without relying on pretrained score functions or external denoisers, this approach still remains adaptive to arbitrary forward operators and noisy observations, making it highly flexible and broadly applicable. We demonstrate the effectiveness of our approach on a variety of linear inverse problems, showing that self-diffusion achieves competitive or superior performance compared to other methods.

• The paper introduces a self-diffusion framework that iteratively refines solutions by alternating between noising and self-denoising steps.
• It employs a novel noise schedule and exploits inherent spectral biases, achieving robust performance in applications like MRI reconstruction and image inpainting.
• The method demonstrates competitive PSNR and SSIM results, highlighting its effective generalization without relying on external data-driven priors.

Self-Diffusion for Solving Inverse Problems

Self-diffusion is a newly proposed framework for addressing inverse problems, such as those frequently encountered in imaging applications. The method circumvents the need for pretrained generative models and instead employs an iterative process of alternating between noising and denoising steps to refine solutions progressively.

Introduction

Inverse problems are prevalent in various domains, notably in imaging applications such as MRI reconstruction and image denoising. Traditional approaches have relied heavily on prior information, often leveraging Bayesian frameworks to integrate observed data and assumptions about the source. While handcrafted priors and supervised learning methods have been employed historically, these approaches can struggle under data scarcity and may lack robustness.

Recent advancements in generative modeling, particularly diffusion models, have demonstrated superior capabilities in capturing complex data distributions. However, these methods generally require extensive curated datasets for training. In contrast, implicit approaches like Deep Image Prior (DIP) exploit neural networks' inductive biases without needing pretraining, although such methods are sensitive to hyperparameters and prone to premature convergence.

Proposed Methodology: Self-Diffusion

Self-diffusion is proposed as a novel approach that leverages the neural networks' spectral bias, which tends to reconstruct smooth, low-frequency structures initially, progressively refining to high-frequency details. The framework operates without pretrained models, relying on an iterative, self-contained process that alternates between noising and self-denoising steps.

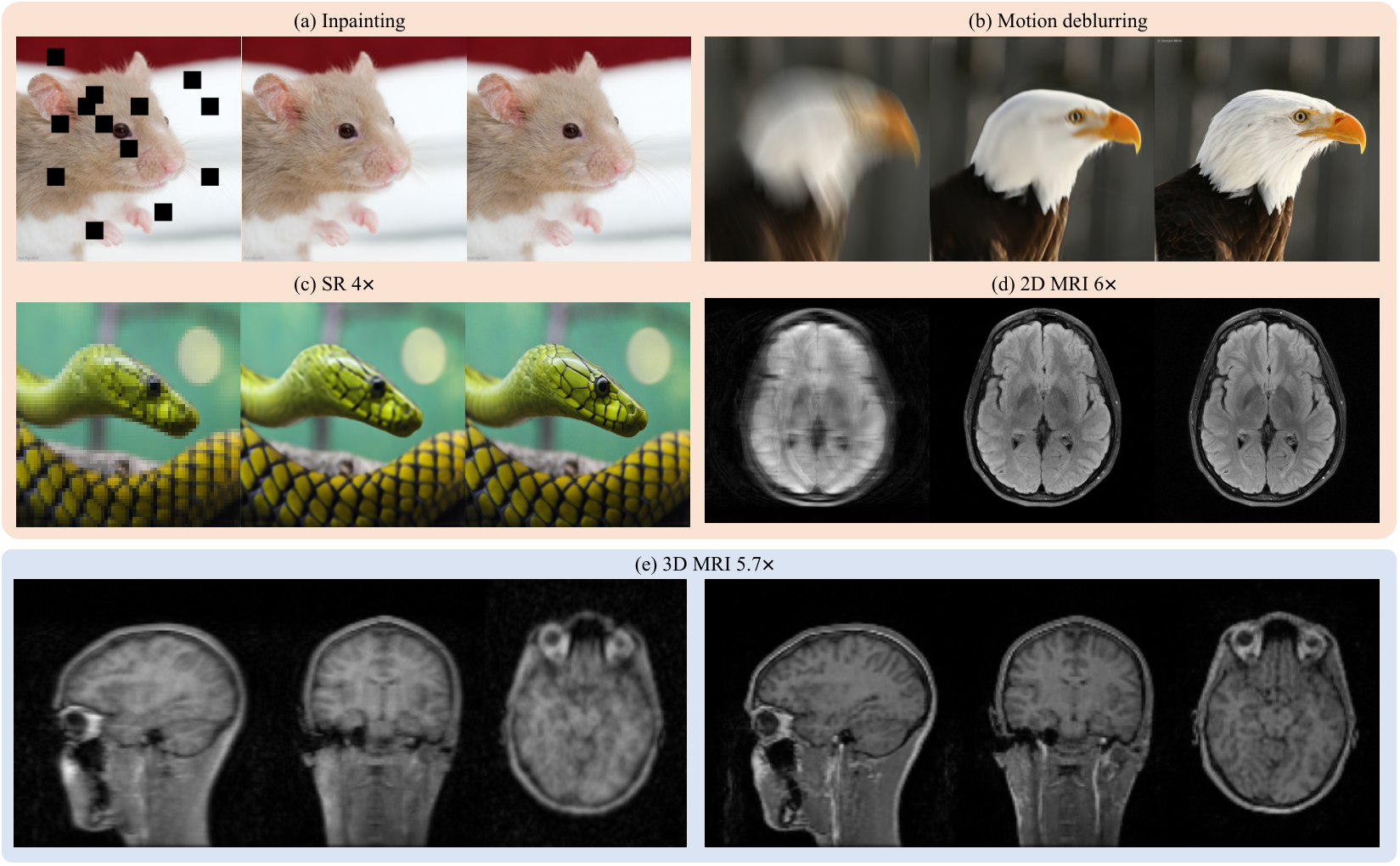
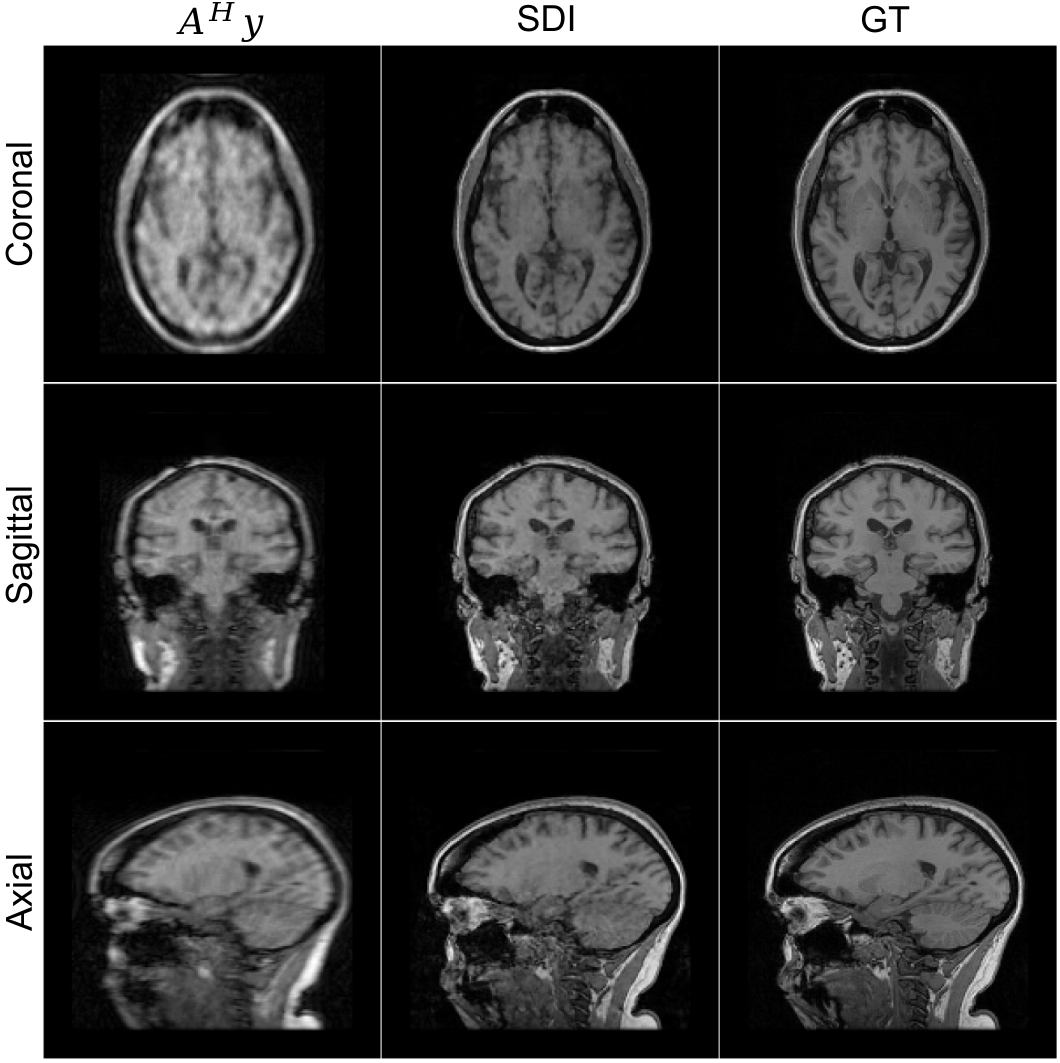
Figure 1: Demonstration of self-diffusion applied to various inverse problems across natural and medical imaging domains.

Each step consists of adding noise to the current estimate and employing a self-denoiser—a randomly initialized convolutional network trained iteratively. The network leverages a noise schedule that modulates the learning dynamics, progressively focusing from low-frequency global structures to high-frequency local details.

Figure 2: Overview of the self-diffusion framework. At each diffusion step $t$, Gaussian noise is added to the current estimate.

Theoretical Foundations

Self-diffusion is founded on the observation that the denoising process in diffusion models traverses from low to high frequencies. By drawing parallels with proximal optimization, self-diffusion employs an implicit regularization that systematically biases learning towards reconstructing natural-looking images.

The central theoretical contributions include a convergence proof demonstrating that the framework's denoiser implicitly enforces signal structure consistent with observed measurements. Moreover, by white-box derivations and Fourier domain analyses (see Appendix), self-diffusion effectively penalizes high-frequency variations, naturally aligning with the spectral bias of neural networks.

Applications and Performance

Self-diffusion has been evaluated across a range of applications, including:

• Medical Imaging (MRI Reconstruction): Demonstrated competitive performance on both 2D and 3D MRI datasets, surpassing traditional methods like Aseq and DIP in PSNR and SSIM metrics.

  Figure 3: Reconstruction of a 3D T1-weighted brain MRI using self-diffusion from 8x undersampled measurements.

• Low-Level Vision Tasks: The framework was applied to tasks like image inpainting, motion deblurring, and super-resolution, consistently achieving superior image quality against baselines like DIP.

Self-diffusion exhibited robustness to initialization while consistently facilitating a coarse-to-fine reconstruction paradigm. The method was showcased to generalize across various tasks, further affirmed by open-sourced implementation codes.

Implications and Future Work

Self-diffusion's performance across diverse inverse problems underscores its ability to generalize without requiring task-specific training. The algorithm's reliance on architectural spectral biases, rather than external data-driven priors, implies potential applications in privacy-sensitive contexts where data scarcity is a concern.

Future developments might explore adaptive noise schedules, integration with neural architecture search frameworks, or hybridizing with small-scale pretrained models to enhance capabilities further.

Conclusion

Self-diffusion introduces a flexible, self-supervised framework leveraged through intrinsic network biases and diffusion processes to address a spectrum of inverse problems effectively. With a noise-modulated spectral bias, the method ensures robust, scalable solutions across diverse applications, highlighting a promising avenue for further research in data-limited environments.