JSTprove: Pioneering Verifiable AI for a Trustless Future (2510.21024v1)
Abstract: The integration of ML systems into critical industries such as healthcare, finance, and cybersecurity has transformed decision-making processes, but it also brings new challenges around trust, security, and accountability. As AI systems become more ubiquitous, ensuring the transparency and correctness of AI-driven decisions is crucial, especially when they have direct consequences on privacy, security, or fairness. Verifiable AI, powered by Zero-Knowledge Machine Learning (zkML), offers a robust solution to these challenges. zkML enables the verification of AI model inferences without exposing sensitive data, providing an essential layer of trust and privacy. However, traditional zkML systems typically require deep cryptographic expertise, placing them beyond the reach of most ML engineers. In this paper, we introduce JSTprove, a specialized zkML toolkit, built on Polyhedra Network's Expander backend, to enable AI developers and ML engineers to generate and verify proofs of AI inference. JSTprove provides an end-to-end verifiable AI inference pipeline that hides cryptographic complexity behind a simple command-line interface while exposing auditable artifacts for reproducibility. We present the design, innovations, and real-world use cases of JSTprove as well as our blueprints and tooling to encourage community review and extension. JSTprove therefore serves both as a usable zkML product for current engineering needs and as a reproducible foundation for future research and production deployments of verifiable AI.
Summary
- The paper presents JSTprove, a toolkit that abstracts zero-knowledge proofs for ML inference, making verifiable AI accessible to developers.
- It details a modular pipeline for ONNX models, including parsing, quantization, circuit compilation, witness generation, and proof verification.
- Benchmarking validates ECC total cost as a reliable predictor of resource usage, demonstrating linear scaling of compute and memory with model complexity.
JSTprove: A Developer-Facing Pipeline for Verifiable AI Inference
Motivation and Context
The paper presents JSTprove, a developer-oriented toolkit for zero-knowledge machine learning (zkML) inference, addressing the growing need for verifiable AI in domains where trust, privacy, and correctness are paramount. As AI systems increasingly impact critical sectors—healthcare, finance, cybersecurity—the ability to cryptographically verify model inferences without exposing sensitive data is essential. JSTprove abstracts the complexity of zero-knowledge proofs (ZKPs) and circuit construction, making verifiable inference accessible to ML engineers without deep cryptographic expertise.
System Architecture and Workflow
JSTprove orchestrates an end-to-end pipeline for verifiable inference on ONNX models, leveraging Polyhedra Network's Expander backend and Expander Compiler Collection (ECC). The workflow consists of:
- Model Import and Parsing: Accepts ONNX models, extracts computational graphs, weights, and activations.
- Quantization: Converts floating-point tensors to fixed-point integers using a dyadic scaling factor, preparing them for finite-field arithmetic.
- Circuit Compilation: Translates the quantized graph into an arithmetic circuit, mapping each layer to ZKP-friendly constraints.
- Witness Generation: Executes quantized inference, recording outputs and auxiliary values as a witness.
- Proof Generation: Uses Expander's GKR/sumcheck-based backend to generate a proof of correct inference.
- Verification: Validates the proof against all artifacts, ensuring faithful execution.
- CLI Exposure: All stages are accessible via a simple command-line interface, supporting reproducible workflows.
This modular design supports core neural operations (GEMM, Conv2D, ReLU, MaxPool) and is extensible to additional layers.
Figure 1: JSTprove pipeline stages, showing the flow from ONNX model import through quantization, circuit compilation, witness generation, proof, and verification.
Circuit Design and Quantization
JSTprove's circuit design is documented in open-source zkML Blueprints, providing mathematical proofs, pseudocode, and ECC-based Rust implementations for primitives such as matrix multiplication, convolution, max pooling, and ReLU. The system employs bitstring decomposition for range checks, enabling enforcement of value bounds, sign extraction for ReLU, and correctness in quantized arithmetic.
Quantization uses a fixed-point scheme: for scaling factor , each float is mapped to . Multiplications are rescaled via quotient-remainder checks, with circuit constraints ensuring soundness. The current approach is constraint-heavy, as every product requires a bit-decomposition range check, but it is transparent and auditable.
Figure 2: Depth = 1 CNN architecture, illustrating the initial block structure used in benchmarking.
Benchmarking and Performance Analysis
JSTprove's performance was evaluated on depth- and breadth-swept CNN families. Key findings include:
- Resource Scaling: ECC's total cost metric (a weighted sum of gate and constraint counts) reliably predicts runtime and memory usage across compilation, witness generation, proof, and verification phases.
- Depth Sweep: Increasing network depth (with fixed input size) leads to linear growth in circuit complexity and resource usage, except for anomalies due to architectural changes (e.g., pooling affecting FC layer size).
- Breadth Sweep: Increasing input spatial size causes super-linear growth in compile time and memory, with large models exceeding available memory.
- Artifact Sizes: Circuit file size grows steadily with model complexity; witness and proof sizes plateau within domain buckets due to workspace allocation.
Figure 3: Compile (depth 1 excluded), showing linear scaling of compile time with parameter count for depths 2–16.
Figure 4: Compile (depth 1 excluded), showing peak memory scaling with parameter count for depths 2–16.
Figure 5: Compile (depth 1 excluded). Outliers removed, demonstrating robust linear scaling after anomaly exclusion.
Figure 6: Compile (depth 1 excluded). Outliers removed, confirming the reliability of ECC's total cost as a predictor of resource usage.
The benchmarking methodology included robust outlier detection (MAD-based), ensuring that transient system effects did not skew scaling analyses.
Transparency, Auditability, and Extensibility
JSTprove emphasizes transparency by publishing all circuit designs, mathematical derivations, and code as open-source zkML Blueprints. This enables external audit, reproducibility, and community-driven extension. The system's CLI and artifact management further support explicit, reproducible workflows.
Implementation Considerations and Future Directions
- Constraint Overhead: The current quantization and circuitization strategies introduce significant overhead, especially in matrix multiplications and range checks.
- Optimizations: Future work includes integrating lookup-based range checks, probabilistic verification (e.g., Freivalds' algorithm for matrix multiplication), and adaptive quantization to reduce constraint counts.
- Scalability: Enabling GPU-based proving via Expander's zkCUDA support is expected to yield substantial speedups for large circuits.
- Extensibility: The modular architecture allows for incremental addition of new neural operators and circuit optimizations.
Practical and Theoretical Implications
JSTprove demonstrates that developer-accessible zkML is feasible for realistic neural architectures, providing a reproducible baseline for verifiable inference. The system's open design and explicit control metrics (ECC total cost) facilitate rigorous benchmarking and incremental improvement. The approach is well-suited for deployment in privacy-sensitive, high-assurance domains, and provides a foundation for future research in scalable, transparent AI verification.
Conclusion
JSTprove delivers a practical, transparent pipeline for verifiable AI inference, abstracting cryptographic complexity and enabling reproducible zkML workflows for ML engineers. Its benchmarking establishes ECC total cost as a reliable control axis for scaling, and its open-source blueprints foster community engagement and auditability. While current implementations incur measurable overhead, the system is positioned for rapid optimization and extension, supporting the evolution of verifiable AI from prototype to production scale.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces JSTprove, a tool that helps people check whether an AI’s answer was computed correctly, without revealing the private data or the secret details of the model. Think of it like getting a trustworthy “math receipt” for each AI decision. This is especially useful in areas like healthcare, finance, and cybersecurity, where mistakes or cheating could be costly or unfair.
What questions does the paper try to answer?
The paper asks:
- How can we prove an AI made its prediction the right way, without exposing private inputs or the model’s internals?
- How can we make these proofs easy for regular AI engineers to create and verify, without needing to be cryptography experts?
- What does it cost (in time and memory) to make these proofs for real neural networks, and how can we predict that cost?
How does JSTprove work? (Simple explanation of the approach)
JSTprove builds on a privacy technology called “zero-knowledge proofs” (ZKPs). In everyday terms, a ZKP lets you prove you followed the rules of a calculation without showing your secret data. Imagine proving you solved a puzzle correctly without revealing the puzzle itself.
Here’s what JSTprove does behind the scenes:
- It takes a trained AI model in a common format called ONNX (like a universal file type for models).
- It converts the model’s decimal numbers into integers by scaling them, similar to turning dollars into cents so you can avoid decimals. This is called quantization.
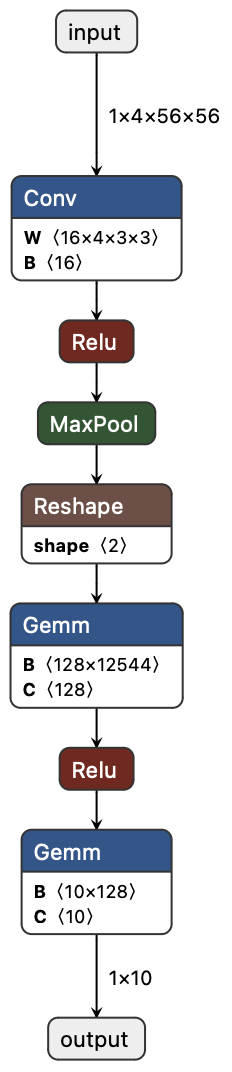
- It turns the model into a big checklist of math constraints (an “arithmetic circuit”). This circuit describes exactly how each layer (like Conv2D, ReLU, MaxPool, and fully connected layers) should compute.
- It runs your input through the quantized model and records all the intermediate values needed to prove it did the right steps. This record is called a witness.
- It creates a zero-knowledge proof that the model followed the circuit correctly on that input.
- Anyone can verify the proof to be sure the AI followed the rules, without seeing the private input.
You can run the whole process from a simple command line. A short, friendly way to remember it:
- compile: prepare the circuit from your model
- witness: run the model and capture the necessary data
- prove: generate the proof
- verify: check the proof
What did they build and test?
- JSTprove connects a developer-friendly front end to a powerful proving engine called Expander (from Polyhedra Network). You don’t need to know cryptography to use it.
- It supports common neural network pieces: fully connected layers, Conv2D, ReLU, and MaxPool.
- It comes with open “blueprints” that explain the math behind the circuits, so others can audit and improve them.
- The authors tested JSTprove on families of convolutional neural networks (CNNs) and measured how long each step takes and how much memory it uses.
Main findings and why they matter
- End-to-end proofs work today: JSTprove can prove and verify real CNN inferences, start to finish.
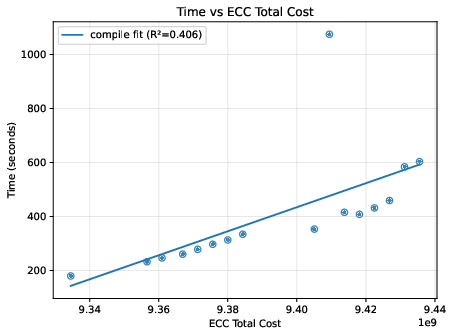
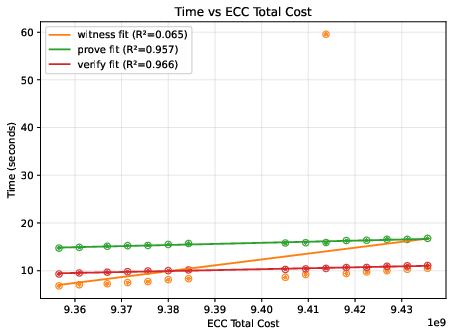
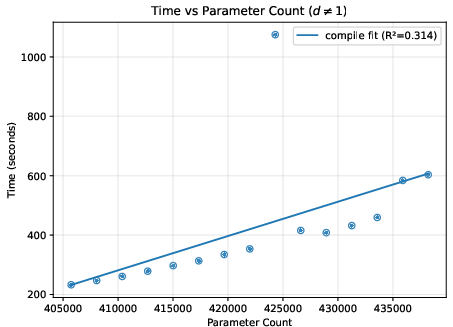
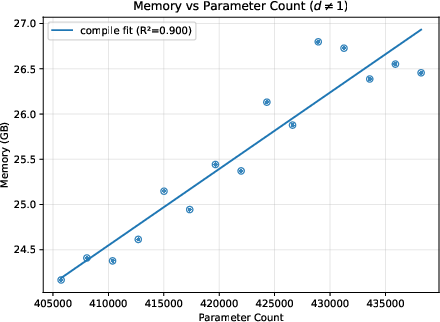
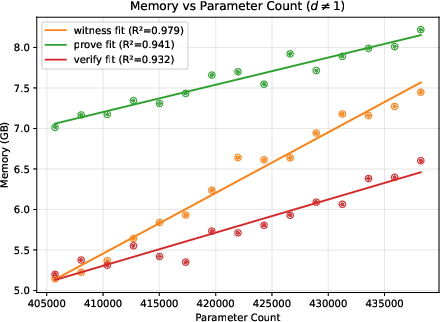
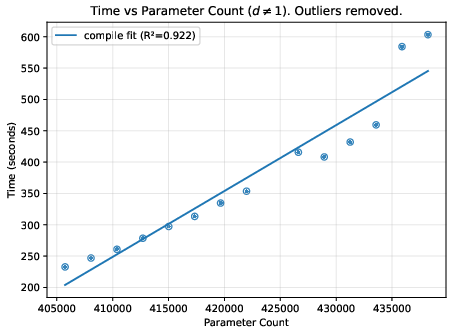
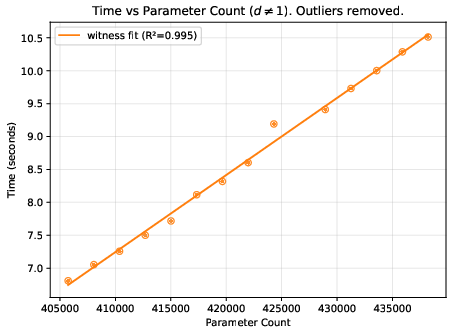
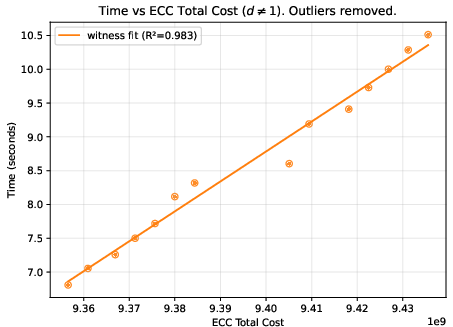
- A helpful “difficulty score”: They found a metric called “total cost” (reported by the Expander compiler) that predicts how much time and memory the process will use. This is more reliable than just counting model parameters, because two models with similar parameter counts can create very different amounts of proof work.
- Scaling behavior:
- Deeper networks generally increase time and memory roughly in line with the total cost score.
- Bigger input images can make things grow quickly (sometimes more than you’d expect), because many more calculations are needed per layer.
- On their test machine, the largest case ran out of memory at the compile step, showing where practical limits are today.
- Proof and file sizes: Proof files stayed fairly small and didn’t grow much, while the “compiled circuit” file grew steadily with model complexity. Witness files tended to grow in steps.
Why this matters:
- Trust without exposure: You can prove an AI followed the rules without showing sensitive data—good for privacy and fairness.
- Usability: AI engineers can use JSTprove through a simple interface, instead of learning advanced cryptography.
- Planning: Teams can estimate resource needs using the total cost metric before they commit to large models.
What could this change in the real world?
- Safer AI decisions: Hospitals, banks, and security teams could demand a proof that an AI decision was computed correctly—no more “just trust us.”
- Privacy by default: Sensitive inputs (like medical images or financial records) remain private while still allowing others to verify the correctness of the result.
- Wider adoption: Because the tool is easier to use and open source, more developers can build verifiable AI systems.
- Clear roadmap: The authors outline practical upgrades—like faster checks for matrix math (e.g., using Freivalds’ algorithm), smarter range checks, better data handling, and GPU acceleration—to make the system faster and more memory-efficient over time.
Takeaway
JSTprove is a step toward a future where AI doesn’t just give answers—it also provides a compact proof that those answers were computed correctly, without revealing secrets. It hides the cryptography behind a friendly tool, shares open blueprints for transparency, and offers a realistic path to bring verifiable AI into everyday use.
Knowledge Gaps
Knowledge Gaps, Limitations, and Open Questions
Below is a consolidated list of what remains missing, uncertain, or unexplored in the paper. Each item is phrased to make it actionable for future work.
Scope and Model Coverage
- Limited operator support (GEMM, Conv2D, ReLU, MaxPool); no circuits for common layers such as batch/layer normalization, average pooling, residual connections, softmax/sigmoid/tanh, leaky/parametric ReLU, attention, transformers, RNNs/LSTMs/GRUs, or embeddings—define a roadmap and prioritize high-impact ops (e.g., LayerNorm, attention).
- No demonstrated support for sequence models or LLMs; evaluate feasibility and constraints for transformer/attention blocks under the chosen backend.
- No batching/multi-input inference; add circuits and pipeline logic for batched proofs to amortize proving costs across inputs.
Quantization and Accuracy
- Fixed-point quantization uses a single power-of-two scale () and floor rounding; evaluate per-layer/per-channel scales, alternate rounding (nearest, stochastic), and mixed-precision schemes to reduce quantization error.
- No methodology to choose scaling parameters (, ) automatically; implement calibration procedures that bound dynamic ranges per layer and prevent wraparound modulo .
- No empirical analysis of accuracy degradation from quantization; benchmark pre- and post-quantization accuracy across datasets and architectures, and report error bounds induced by quotient–remainder checks.
- No handling of activation/weight outliers (clipping, saturating arithmetic, or learned scales); explore robust quantization strategies that maintain model fidelity in circuits.
- Absence of circuits for non-polynomial activations (e.g., softmax/exponential/log); explore polynomial/rational approximations or lookup-based implementations with quantified approximation error.
Circuit Design and Soundness
- Range checks rely on bit-decomposition using ECC’s unconstrained bit operations; provide a formal soundness proof in the ECC/Expander semantics and validate there are no edge cases near field boundaries.
- Lookup-based range checks are noted as future work; implement and benchmark PLONK-style lookup arguments or ECC-native lookups to reduce constraint counts.
- Matrix multiplication currently verifies every product; Freivalds’ randomized check is not implemented—integrate it, quantify soundness error (), and measure real constraint reductions.
- ReLU sign inference via MSB reuse depends on balanced residue conventions; formally prove correctness under all chosen field sizes and scaling configurations and add safeguards for edge cases.
- Formal specification of the exact zero-knowledge statement is missing (which wires are public/secret, what commitments are opened); publish a machine-readable spec (e.g., JSON/DSL) that unambiguously defines the proved relation.
Security, Privacy, and Threat Model
- Unclear threat model: specify whether inputs, weights, and intermediate activations are treated as private, what is revealed to verifiers, and how integrity is enforced when weights are proprietary.
- No mechanism to keep model weights private while proving correct inference; add commitments to weights and support proofs with hidden parameters (private-weight inference).
- Security assumptions of Expander/ECC not articulated (commitment scheme, sumcheck details, soundness/completeness/zero-knowledge guarantees, transparency/trusted setup); document assumptions, parameter choices, and audit status.
- No discussion of side-channel risks (timing, memory footprint, artifact sizes) that could leak private information; add mitigations and a leakage analysis for CLI and artifact handling.
- Randomness handling (seeding, reproducibility, and privacy of random coins) unspecified; define policies for deterministic builds vs. cryptographically secure randomness in proofs.
Performance and Scalability
- Compile-phase OOM at 36 GB for input size 112 indicates memory hotspots; instrument the pipeline to pinpoint allocations (ECC builder, serialization, constraint generation) and implement streaming/chunked circuit compilation.
- No GPU proving results despite mentioning zkCUDA; conduct controlled GPU benchmarks, report speedups, and characterize GPU memory limits.
- No proof aggregation or recursion; add support for aggregating multiple inferences or recursive composition to reduce verification costs and enable scalable deployments.
- No distributed/multi-core proving strategies quantified; evaluate parallelization across layers/blocks and measure wall-clock reductions.
- No cost model beyond ECC’s “total cost” metric; develop a predictive estimator mapping ONNX graph features (ops, tensor shapes, scales) to time/memory/proof size to guide users before compile/prove.
Benchmarking Methodology and Coverage
- Benchmarks limited to LeNet-style CNNs on a single machine (Mac M3 Max); replicate on Linux servers, GPUs, and varied hardware to assess portability and performance variability.
- Lack of end-to-end accuracy+performance benchmarks on real datasets (e.g., CIFAR/ImageNet) and realistic models; expand evaluations and include accuracy retention post-quantization.
- No head-to-head comparisons with other zkML frameworks (EZKL, ZKTorch, DeepProve, zkPyTorch); perform comparative studies on identical models to quantify time/memory/proof size and usability differences.
- Witness/proof size behavior described qualitatively; provide quantitative analysis of artifact sizes across diverse circuits and tie them to verification costs (e.g., on-chain fees).
Integration, Verification, and Deployment
- No on-chain verification demo (e.g., Ethereum, rollups); integrate verifiers for the chosen backend and report gas/fee costs and proof size impacts.
- Developer UX is CLI-only; add a Python API and MLOps integration (logging, metrics, CI workflows) to broaden adoption.
- Absence of robust error reporting and recovery (e.g., graceful handling of OOM, retries, partial compile/prove); add diagnostic tooling and resumable pipeline stages.
- Lack of formal reproducibility guarantees (artifact hashing, version pinning, deterministic circuit builds); define and enforce a provenance schema for circuits, witnesses, and proofs.
Transparency, Auditability, and Governance
- Open-source blueprints exist, but independent security audits and formal verification of circuits/backends are not reported; commission third-party audits and publish results.
- No governance or review process for circuit updates and parameter changes; establish a transparent change-management workflow (RFCs, test suites, regression checks).
- The interplay between “auditability” (exposing artifacts) and privacy (zero-knowledge) is not operationalized; document what artifacts are safe to publish and provide privacy-preserving audit traces.
Reliability and Robustness
- Outlier runs attributed to transient system factors without systematic mitigation; integrate robust benchmarking harnesses (pin CPU/GPU affinity, thermal monitoring) and statistical controls to reduce noise.
- No robustness analysis to adversarial inputs or malformed ONNX graphs; add validation layers and constraints ensuring well-formed models and input ranges to prevent proof-generation failures or undefined behavior.
- Field size selection () and wraparound avoidance left to care; automate field/scale selection with formal guarantees that all intermediate values remain within safe bounds.
These gaps collectively outline a research and engineering agenda: broaden operator coverage; harden security and privacy guarantees; optimize circuits and memory; expand benchmarking and real-world integration; and formalize the zero-knowledge statements, reproducibility, and audit processes.
Practical Applications
Applications of JSTprove
Below are actionable, real-world applications that follow directly from the paper’s findings, methods, and tooling. Each item names sectors, possible tools/products/workflows that could emerge, and key assumptions or dependencies that affect feasibility.
Immediate Applications
These can be piloted or deployed now with JSTprove’s current capabilities (ONNX models, Conv2D/GEMM/MaxPool/ReLU, CLI-based pipeline, quantized integer arithmetic, Expander/ECC backend), acknowledging the performance envelope demonstrated in the benchmarks.
- Verifiable inference for privacy-sensitive analytics
- Sector: Healthcare, cybersecurity, finance
- Tools/Workflow: Export existing ONNX CNNs, run
compile → witness → prove → verifyto attach a zero-knowledge proof to each prediction; wrap as a microservice (proof-carrying prediction API) for clinical triage, malware detection, or fraud alerts without revealing inputs - Assumptions/Dependencies: Model fits current operator coverage and quantization accuracy budget; runtime/memory within acceptable bounds (e.g., compile can require tens of GB); verifier trusts the model commitment (hash/signature) used in the circuit
- Proof-of-model-use for ML vendors and internal MLOps
- Sector: Software industry, ML platforms
- Tools/Workflow: Add a verification gate in CI/CD and serving pipelines to ensure predictions were produced by the certified model version; store circuit/witness/proof artifacts in an auditable registry
- Assumptions/Dependencies: Stable model registry and artifact hashing; organizational buy-in to audit trails; current CLI integrated into build/deploy tooling
- Off-chain verification for risk scoring and compliance reporting
- Sector: Finance (traditional and DeFi), insurance
- Tools/Workflow: Attach proofs to risk scores/credit decisions so auditors can verify correctness without seeing inputs; integrate ECC total-cost metrics to forecast proving resources
- Assumptions/Dependencies: Off-chain verifiers accept Expander proofs; regulator/auditor processes allow proof-carrying reports; quantization doesn’t materially change decision thresholds
- Privacy-preserving result sharing for data marketplaces
- Sector: Data exchanges, analytics services
- Tools/Workflow: Data owners act as provers and share only outputs plus proofs to buyers; buyers verify without accessing raw data
- Assumptions/Dependencies: Small-to-medium CNNs acceptable; contractual frameworks accept ZKPs as evidence; correct binding of model identity (hash, signature) to the proof
- Contractual assurance in ML procurement
- Sector: Policy, public sector, regulated industries
- Tools/Workflow: Require vendors to deliver proof-carrying predictions during pilot evaluations; include artifact verification in procurement due diligence
- Assumptions/Dependencies: RFPs and contracts explicitly recognize ZK proofs; reviewers trained to run
verifyand match model commitments
- Academic reproducibility and artifact auditing
- Sector: Academia, ML research
- Tools/Workflow: Publish proofs alongside reported results and open-source circuits/blueprints; use JSTprove Blueprints in coursework to teach circuit correctness (range checks, ReLU, max-pool) and quantization design
- Assumptions/Dependencies: Datasets and models exportable to ONNX; paper venues accept proof-carrying artifacts; student hardware sufficient for smaller benchmarks
- Competition and benchmark integrity
- Sector: ML competitions, community leaderboards
- Tools/Workflow: Require contestants to submit predictions plus proofs to certify correct evaluation on hidden test sets; organizers run
verifyto prevent model/metric manipulation - Assumptions/Dependencies: Task models compatible with supported operators; competition infrastructure can ingest artifacts and run verification
- Edge-to-cloud trust handshakes for safety-critical signals (pilot scale)
- Sector: IoT, industrial automation, healthcare devices
- Tools/Workflow: Edge device computes inference locally and supplies proof to a cloud verifier before actuator commands or alerts are accepted
- Assumptions/Dependencies: Latency tolerates current proving times; model sizes fit device memory; trusted model commitments embedded on device
- Proof-carrying prediction logging and governance dashboards
- Sector: Enterprise compliance, MLOps
- Tools/Workflow: Tamper-evident logs that store (input hash, model hash, circuit hash, proof) per prediction; dashboards track verification rates and ECC total cost for capacity planning
- Assumptions/Dependencies: Secure artifact storage; operational processes to sample and re-verify; stable ONNX export across model versions
- Teaching and rapid prototyping in zkML
- Sector: Education, developer enablement
- Tools/Workflow: Use JSTprove’s CLI and the Blueprints repo to build classroom labs on quantization (quotient–remainder checks), bit-decomposition range checks, and simple CNN circuits
- Assumptions/Dependencies: Availability of open models; hardware access for compilation/proving labs; familiarity with ONNX workflows
Long-Term Applications
These require further research, scaling, operator coverage, or productization (e.g., GPU proving via zkCUDA, lookup-optimized range checks, probabilistic matmul verification, more layers/architectures, proof aggregation/batching, on-chain verifiers).
- Verifiable inference for transformers and LLMs at scale
- Sector: Software, education, healthcare, enterprise IT
- Tools/Workflow: Extend operator coverage to attention, layer norms, GELU, etc.; use GPU proving (zkCUDA) and Freivalds-based matmul checks; integrate batching and proof aggregation for throughput
- Assumptions/Dependencies: Circuit optimizations reduce constraints; memory footprint and runtime viable for production; acceptable quantization fidelity for language/vision tasks
- Real-time proof-carrying control in robotics/automotive
- Sector: Robotics, AVs, manufacturing
- Tools/Workflow: Fast proofs verifying perception and control inferences before actuation; PCD (proof-carrying data) across control loops
- Assumptions/Dependencies: Sub-second proving with GPU and specialized gadgets; deterministic models and tight quantization; robust failure modes when proofs cannot be produced
- On-chain verifiable AI services and marketplaces
- Sector: DeFi, decentralized compute, data DAOs
- Tools/Workflow: Publish succinct proofs to smart contracts for automated settlement (e.g., pay-per-correct-inference); standardized verifiers for Expander/GKR circuits
- Assumptions/Dependencies: Chain-side verifier availability and cost; proof size compatible with on-chain constraints; bridging security between off-chain provers and on-chain contracts
- Regulatory “proof-of-inference” standards for high-risk AI
- Sector: Policy, healthcare, finance, employment
- Tools/Workflow: Certification pipelines where AI systems must attach proofs to decisions; auditors verify conformance and track artifact provenance
- Assumptions/Dependencies: Regulators define acceptable proof systems and model commitments; operator coverage matches deployed models; standardized reporting formats
- Fairness and policy-compliance proofs
- Sector: Employment screening, lending, insurance
- Tools/Workflow: Circuits that attest to policy properties (e.g., protected attributes not used, thresholds enforced, monotonicity constraints); proofs accompany each decision
- Assumptions/Dependencies: Formal property encoding in circuits; model design compatible with verifiable constraints; careful threat modeling to prevent proxy-variable leaks
- Federated and cross-border analytics with privacy guarantees
- Sector: Healthcare networks, consortium research, global enterprises
- Tools/Workflow: Participants produce proofs of locally computed inferences on private data; central aggregator verifies and combines results
- Assumptions/Dependencies: Network bandwidth and batching strategies; standardized model commitments; federated orchestration of artifacts and verifiers
- Proof-carrying data pipelines across microservices
- Sector: Enterprise software architectures
- Tools/Workflow: Compose proofs as data flows through multiple services (PCD), enabling end-to-end attestation of transformations and inferences
- Assumptions/Dependencies: Composability of proof systems; manageable proof sizes; consistent identity and versioning across services
- Licensed-model enforcement and provenance in model marketplaces
- Sector: Software, IP licensing
- Tools/Workflow: Vendors ship models with circuit commitments and require proofs of use; audits verify license compliance without revealing model internals
- Assumptions/Dependencies: Strong binding of model identity (hash/watermark) to circuits; legal frameworks recognize cryptographic evidence; secure key management
- Verifiable content moderation and trust signals for platforms
- Sector: Social media, user-generated content
- Tools/Workflow: Attach proofs to moderation decisions confirming the policy-configured model was used; enable transparent appeal processes
- Assumptions/Dependencies: Efficient circuits for large-scale classification; standardized policy circuits; acceptable latency per decision
- Energy and grid forecasting with audit-friendly AI
- Sector: Energy, utilities
- Tools/Workflow: Proof-carrying forecasts for regulators and market participants; batched verification for large time-series models
- Assumptions/Dependencies: Operator coverage for time-series architectures; throughput improvements via GPU proving and aggregation
- Developer SDKs and managed “proof-as-a-service”
- Sector: Software tools, cloud providers
- Tools/Workflow: Python/JS SDKs, REST gateways, managed artifact storage, autoscaling GPU provers; integrations with model registries and CI systems
- Assumptions/Dependencies: Productization of JSTprove pipeline; robust multi-tenant isolation; cost-effective GPU backends
- Education at scale: interactive zkML curricula and labs
- Sector: Education, workforce upskilling
- Tools/Workflow: Courseware and cloud sandboxes for building circuits, quantizing models, and benchmarking proofs; standardized assignments and grading via verification
- Assumptions/Dependencies: Accessible hardware (or cloud credits); stable APIs; broader operator coverage for diverse coursework
Notes on common assumptions/dependencies across applications:
- Current operator coverage is limited (GEMM, Conv2D, ReLU, MaxPool); broader coverage is needed for many long-term scenarios.
- Quantization fidelity must be validated per domain; some decisions are sensitive to rounding/rescaling.
- Proving/verification costs depend on ECC’s total-cost metric; larger inputs and deeper networks can exceed memory without optimizations.
- Trust anchors (signatures/hashes) are crucial to bind model identity and version to circuits and proofs.
- Zero-knowledge proofs hide inputs from verifiers, but the prover still sees inputs; privacy architectures should reflect the intended threat model (client-side proving vs. server-side proving).
- On-chain use requires compatible verifiers and cost controls; off-chain verification is viable now.
Glossary
- arithmetic circuit: An algebraic representation of a computation using gates over a field, used as the object proved in many ZKP systems. "The prover typically represents the computation as an arithmetic circuit and then generates a proof that the circuit was evaluated correctly."
- balanced residue representative: The canonical representative of an integer modulo a prime chosen from a symmetric interval around zero. "provided we adopt the usual convention that each integer is decoded from its balanced residue representative in ."
- bitstring decomposition: Expressing an integer as a sequence of bits inside a circuit to enable checks like ranges or signs. "we outline our design for range checking via bitstring decomposition (to be optimized with lookup tables in future versions)."
- Circom language: A domain-specific language for writing arithmetic circuits used in ZK applications. "a library of circuit templates for the Circom language."
- constraint system: A set of algebraic constraints encoding the correctness conditions of a computation, which a proof system enforces. "a frontend compiles the model into a constraint system or arithmetic circuit"
- dyadic interval: An interval whose length is a power of two, often used to align with binary scaling in fixed-point encodings. "lies in a dyadic interval anchored at $0$"
- Expander: Polyhedra Network’s proving backend that integrates GKR and related techniques for scalable ZK proofs. "Expander's GKR/sumcheck-based backend"
- Expander Compiler Collection (ECC): The frontend toolchain that compiles high-level models into arithmetic circuits for Expander. "using the Expander Compiler Collection (ECC)"
- Freivalds' algorithm: A randomized algorithm for verifying matrix multiplications more efficiently than recomputation. "we plan to integrate Freivalds' algorithm \cite{Freivalds1977}"
- GKR protocol: The Goldwasser–Kalai–Rothblum interactive proof framework for verifying layered arithmetic circuits efficiently. "zkPyTorch is based on the GKR protocol"
- Groth16: A widely used zk-SNARK protocol producing short proofs with fast verification, requiring a trusted setup. "proved using the Groth16 protocol"
- Halo2: A SNARK framework supporting plonkish arithmetization and lookup arguments, used by several zkML tools. "an optimizing compiler from TensorFlow to Halo2 circuits"
- lookup arguments: Proof-system techniques enabling efficient verification of value membership in precomputed tables (e.g., for range checks). "sumchecks, lookup arguments, and polynomial accumulation."
- Mira accumulation scheme: A method for aggregating multiple proofs/claims to reduce verification cost and proof size. "via the Mira accumulation scheme"
- MPC-in-the-Head (MPCitH): A ZK paradigm where the prover simulates a secure multiparty computation and reveals random views to prove correctness. "MPC-in-the-Head (MPCitH) protocols simulate a secure multiparty computation internally"
- ONNX: An interoperable format for ML models enabling portability across frameworks and tooling. "Accepts ONNX models and parses their computational graphs"
- polynomial commitment: A cryptographic primitive allowing a prover to commit to a polynomial and later open its evaluations succinctly. "combines GKR with polynomial commitment techniques"
- polynomial openings: The revealed evaluations (with proofs) of committed polynomials used during verification. "reduce the number of polynomial openings required during verification."
- polynomial relation: An algebraic equation encoding layer behavior so that correct evaluation can be checked via polynomials. "expressed as a polynomial relation"
- post-quantum secure: Resistant to attacks by quantum computers under standard assumptions (e.g., hash-based). "which also makes them plausibly post-quantum secure."
- prime field: A finite field with a prime number of elements, commonly the base field for circuit arithmetic. "over a prime field "
- quantization: Mapping floating-point values to fixed-point integers (often via scaling) to enable finite-field computation in circuits. "we quantize all floating-point weights, activations, and inputs into integers."
- quotient-remainder check: A circuit pattern that enforces correct integer division by constraining a product as dividend = divisor × quotient + remainder within bounds. "quantization is reduced to a quotient-remainder check plus a range constraint."
- range check: A constraint ensuring a value lies within a specified interval, often implemented via bit-decomposition or lookups. "The remainder bound is certified by a range check"
- secure multiparty computation (SMC): Cryptographic techniques enabling joint computation on private inputs without revealing them. "homomorphic encryption and secure multiparty computation"
- sumcheck: An interactive proof subroutine verifying the value of multivariate polynomial sums, widely used in GKR-style systems. "GKR/sumcheck-based backend"
- trusted setup: An initialization phase generating common reference parameters; if compromised, soundness may be at risk. "the type of trusted setup required (circuit-specific, universal, or none)"
- vector-oblivious linear evaluation (VOLE): A cryptographic primitive enabling efficient correlation generation used in modern ZK protocols. "VOLE-based constructions use vector-oblivious linear evaluation as a core building block"
- witness: The private inputs and intermediate values that demonstrate correct circuit execution to the prover. "records the resulting outputs and auxiliary values as a witness."
- Zero-Knowledge Machine Learning (zkML): Applying ZK proofs to ML to verify correct inference without revealing private inputs or models. "Zero-Knowledge Machine Learning (zkML)"
- zero-knowledge proofs (ZKPs): Cryptographic proofs that reveal no information beyond the truth of the statement being proved. "zkML uses zero-knowledge proofs (ZKPs) to verify that a model's outputs are derived by correct execution"
- zk-SNARKs: Succinct non-interactive zero-knowledge arguments with short proofs and fast verification, often requiring trusted setup. "Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (zk-SNARKs) produce very short proofs"
- zk-STARKs: Transparent, scalable zero-knowledge arguments relying on hash-based assumptions, avoiding trusted setup. "Zero-Knowledge Scalable Transparent Arguments of Knowledge (zk-STARKs) avoid trusted setup altogether"
Collections
Sign up for free to add this paper to one or more collections.