First Observation of Dispersive Shock Waves in an Electron Beam (2510.19786v1)

Abstract: Dispersive shock waves (DSWs) are expanding nonlinear wave trains that arise when dispersion regularizes a steepening front, a phenomenon observed in fluids, plasmas, optics, and superfluids. Here we report the first experimental observation of DSWs in an intense electron beam, using the University of Maryland Electron Ring (UMER). A localized induction-cell perturbation produced a negative density pulse that evolved into a leading soliton-like peak followed by an expanding train of oscillations. The leading peak satisfied soliton scaling laws for width^2 vs inverse amplitude and velocity vs amplitude, while the total wave-train width increased linearly with time, consistent with Korteweg--de Vries (KdV) predictions. Successive peaks showed decreasing amplitude and velocity toward the trailing edge, in agreement with dispersive shock ordering. These results demonstrate that intense charged particle beams provide a new laboratory platform for studying dispersive hydrodynamics, extending nonlinear wave physics into the high-intensity beam regime.

• The paper presents the first experimental observation of dispersive shock waves (DSWs) in a high-intensity electron beam using the UMER facility.
• It employs numerical simulations and precise current measurements to validate KdV theory through observed soliton scaling laws and linear wave-train expansion.
• These findings open new avenues in accelerator physics by establishing a platform for studying nonlinear dispersive hydrodynamics in beam transport.

First Observation of Dispersive Shock Waves in an Electron Beam

Introduction

This paper presents the first experimental observation of dispersive shock waves (DSWs) in an intense electron beam, utilizing the University of Maryland Electron Ring (UMER) as the experimental platform. DSWs are expanding nonlinear wave trains that regularize steep fronts through the interplay of dispersion and nonlinearity, a phenomenon previously observed in fluids, plasmas, nonlinear optics, and superfluids. The work extends the paper of nonlinear dispersive hydrodynamics into the high-intensity charged particle beam regime, providing a new laboratory system for investigating DSW formation, evolution, and scaling laws.

Theoretical Framework

The dynamics of small-amplitude density perturbations in dispersive, nonlinear media are governed by the Korteweg–de Vries (KdV) equation:

$$\frac{\partial u}{\partial t} + \alpha u \frac{\partial u}{\partial z} + \beta \frac{\partial^3 u}{\partial z^3} = 0$$

where $u(z,t)$ is the density perturbation, $\alpha$ is the nonlinear coefficient, and $\beta$ is the dispersion parameter. The KdV equation admits both solitary (soliton) and cnoidal wave solutions. For negative initial perturbations, the system undergoes a gradient catastrophe, which is regularized by dispersion into an expanding oscillatory front—a DSW. Theoretical predictions indicate that the leading peak of a DSW should exhibit soliton-like scaling laws, while the overall wave-train width expands linearly with time, with the expansion rate proportional to the initial amplitude difference across the shock.

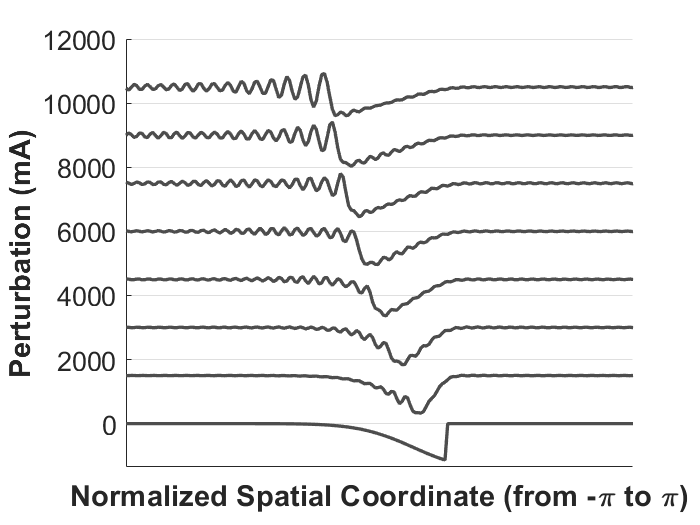
Figure 1: Numerical KdV solution for a negative initial perturbation, showing the evolution into an expanding oscillatory wave train characteristic of a DSW.

Simulation Methodology

Numerical simulations were performed using the WARP particle-in-cell code, initializing a 10-keV electron beam with uniform density and transverse velocity. A localized, one-time longitudinal electric field introduced a narrow Gaussian velocity perturbation, which, after a single pass, produced two opposite-polarity current peaks. The simulation domain was periodic axially and conducting radially, with 16 million macroparticles, 1 ns time steps, and high spatial resolution. The simulation captured the qualitative evolution of the DSW, including the formation of a leading peak and trailing oscillatory structure.

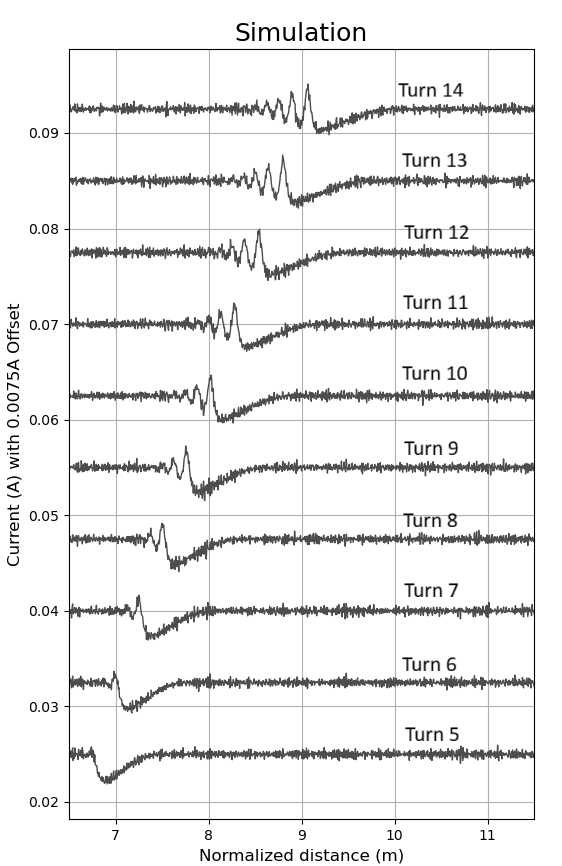
Figure 2: Simulated beam current evolution in WARP, showing the formation and expansion of a DSW following a negative density perturbation.

Experimental Setup and Measurement

The experimental protocol involved injecting a single 100 ns rectangular electron bunch into UMER, with a controlled velocity modulation applied via an inline induction cell to generate a negative density perturbation. Beam current was measured per revolution using a wall current monitor located 7.67 m downstream. The evolution of the current perturbation was tracked over successive turns, with background subtraction to isolate the DSW features. No frequency filtering was applied, preserving the full oscillatory structure.

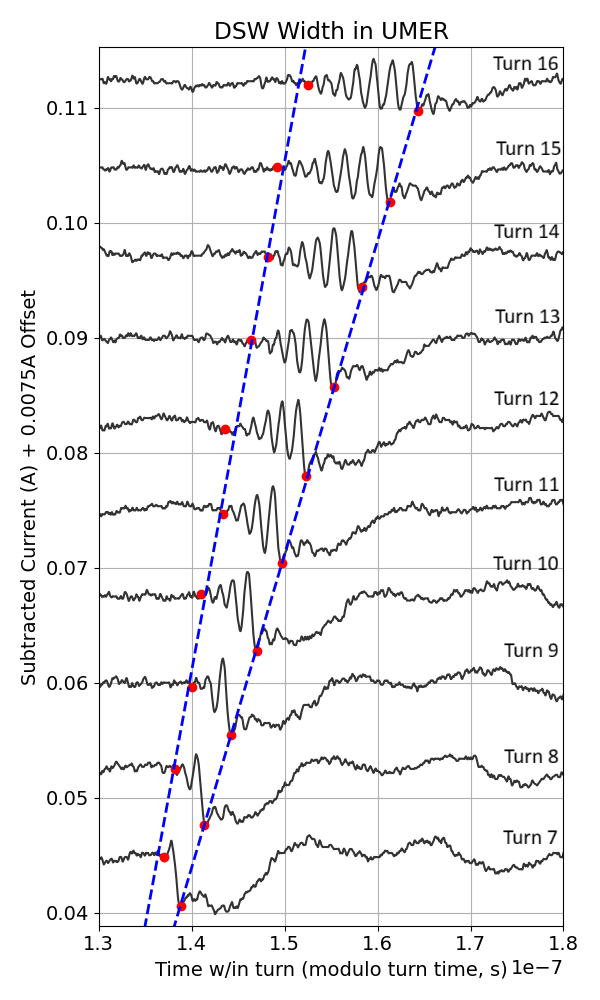
Figure 3: Measured current perturbation in UMER over successive revolutions, demonstrating the formation and linear expansion of the DSW.

Quantitative Analysis and Scaling Laws

Analysis focused on turns 10–16, where the DSW structure was fully developed. The leading peak was found to obey soliton scaling laws:

• Velocity vs amplitude: linear scaling with reduced $\chi^2 = 1.16$
• Squared width vs inverse amplitude: linear scaling with reduced $\chi^2 = 0.51$

The total width of the DSW expanded linearly with turn number, consistent with KdV theory, with a measured expansion rate of $(6.02 \pm 0.31) \times 10^{-3}~\mathrm{s/s}$ for a 30 mA initial perturbation. Reducing the initial perturbation to 20 mA yielded a slower expansion rate of $(4.04 \pm 0.33) \times 10^{-3}~\mathrm{s/s}$, in agreement with the predicted linear dependence on amplitude. Successive peaks exhibited decreasing amplitude and velocity toward the trailing edge, consistent with dispersive shock ordering.

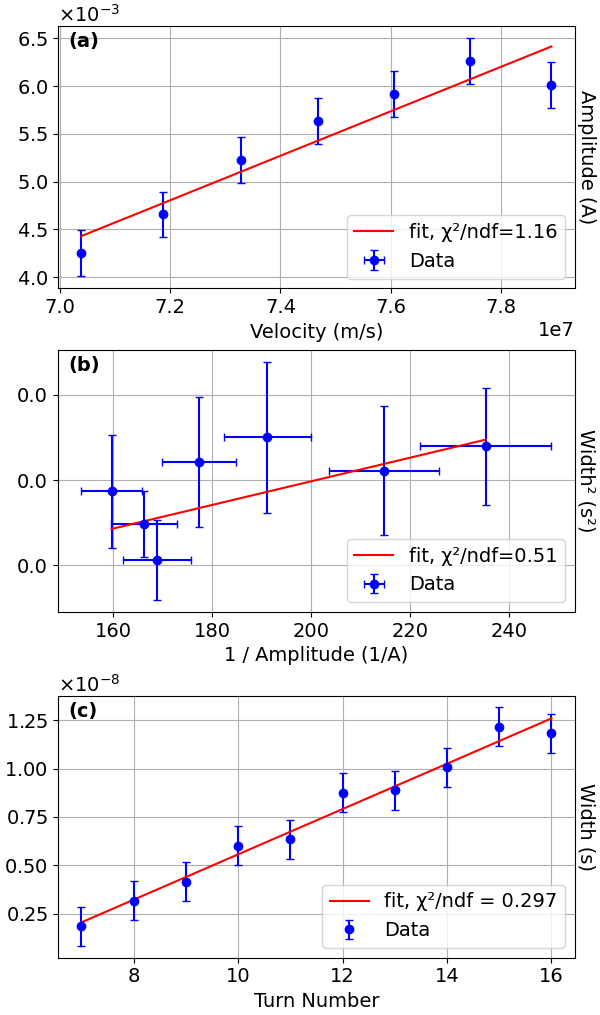
Figure 4: (a) Squared width vs inverse amplitude and (b) velocity vs amplitude for the leading peak, both showing linear scaling; (c) DSW width vs turn number, demonstrating linear expansion.

Implications and Future Directions

The observation of DSWs in a space-charge–dominated electron beam establishes intense charged particle beams as a viable platform for studying nonlinear dispersive hydrodynamics. The results confirm that DSW dynamics, previously confined to other physical systems, are accessible in high-intensity beam environments. This has direct implications for accelerator physics, where space-charge effects are prominent, and for the paper of beam-driven radiation sources and astrophysical plasma analogues.

The UMER platform enables controlled studies of DSW formation, long-time evolution, and interactions with solitons. Future research directions include the investigation of soliton–DSW collisions, modulational instabilities, and the interplay between different nonlinear excitations. The scalability of these dynamics to high-energy accelerators suggests potential relevance for beam transport, stability, and the design of next-generation accelerator systems.

Conclusion

This work provides the first experimental evidence of dispersive shock waves in an intense electron beam, with quantitative agreement between theory, simulation, and experiment. The leading peak of the DSW follows soliton scaling laws, and the wave-train width expands linearly with time, as predicted by KdV theory. These findings extend the paper of nonlinear wave physics into the high-intensity beam regime and open new avenues for research in dispersive hydrodynamics, accelerator science, and plasma physics.