Effects of Dynamical Capture on two equal-mass non-spinning black holes (2510.19699v1)

Abstract: Dynamical captures of black holes are unique events that provide an exceptional opportunity to probe the strong-field regime of gravitational physics. In this article, we perform numerical relativity simulations to study the events of dynamical capture of two equal-mass non-spinning black holes. We consider a suite of scenarios within a range of initial linear momenta ($p/M=0.095-0.75$) and incidence angles ($\theta=6.36^\circ-2.83^\circ$), and study the emitted Weyl scalar ($\Psi_4$) of each case, as well as the spins and masses of the black holes before and after they merge. We provide a simple analytical model which accurately fits the gravitational-wave emission. We study the dependence of the time-interval between the capture and the merger emissions with respect to the incidence angle, which can be well parametrized by a first-order divergent behavior, allowing to find the angle that separates a scattering event from a dynamical capture. We also find that, in general, the parameters that model the first emission can be well described by linear or exponentially decaying functions in terms of the incidence angle, while others display more complex behaviors that offer valuable insights into the nature of these events.

• The paper demonstrates that dynamical capture events yield a two-stage gravitational wave emission with an initial burst during hyperbolic encounters followed by a strong merger signal.
• The paper utilizes advanced numerical simulations with the Einstein Toolkit and adaptive mesh refinement to study gravitational waveforms and black hole property evolution.
• The paper finds that horizon absorption and spin induction contribute to measurable changes in mass, spin, and radiated energy, providing insights for future gravitational wave detection.

Effects of Dynamical Capture on Two Equal-Mass Non-Spinning Black Holes

Introduction

This work presents a systematic numerical relativity (NR) paper of dynamical capture (DC) events involving two equal-mass, non-spinning black holes (BHs). DCs are characterized by initially unbound BHs that, through gravitational wave (GW) emission during a close hyperbolic encounter (CHE), lose sufficient energy and angular momentum to become bound and subsequently merge. The paper is motivated by the astrophysical relevance of DCs in dense environments, such as primordial black hole (PBH) clusters, and the need for accurate waveform models for GW detection and parameter estimation. The authors focus on the phenomenology of GW emission, the evolution of BH properties, and the development of a robust analytical model for the emitted Weyl scalar $\Psi_4$.

Numerical Framework and Initial Conditions

The simulations utilize the Einstein Toolkit, employing the BSSN formulation for spacetime evolution, adaptive mesh refinement via Carpet, and puncture initial data generated by TwoPunctures. Apparent horizons are tracked with AHFinderDirect, and quasi-local measures of mass and spin are extracted using QuasiLocalMeasures. The Weyl scalar $\Psi_4$ is computed for GW extraction.

The initial configuration consists of equal-mass BHs ($q=1$), zero initial spins, and symmetric linear momenta $p/M$ ranging from $0.095$ to $0.75$. Incidence angles $\theta$ span $2.83^\circ$ to $6.36^\circ$, corresponding to impact parameters $b/M$ from $4.9$ to $11.0$. The initial separation is fixed at $d=100M$, and all quantities are expressed in geometrized units ($G=c=1$).

Dynamical Evolution and Gravitational Wave Emission

DCs exhibit a two-stage GW emission profile: an initial burst during the CHE, followed by a second, more intense burst at merger. The CHE phase is characterized by a rapid close approach, significant horizon absorption (tidal heating and torquing), and spin induction. The subsequent merger produces a strong GW signal and a final remnant BH with distinct mass and spin properties.

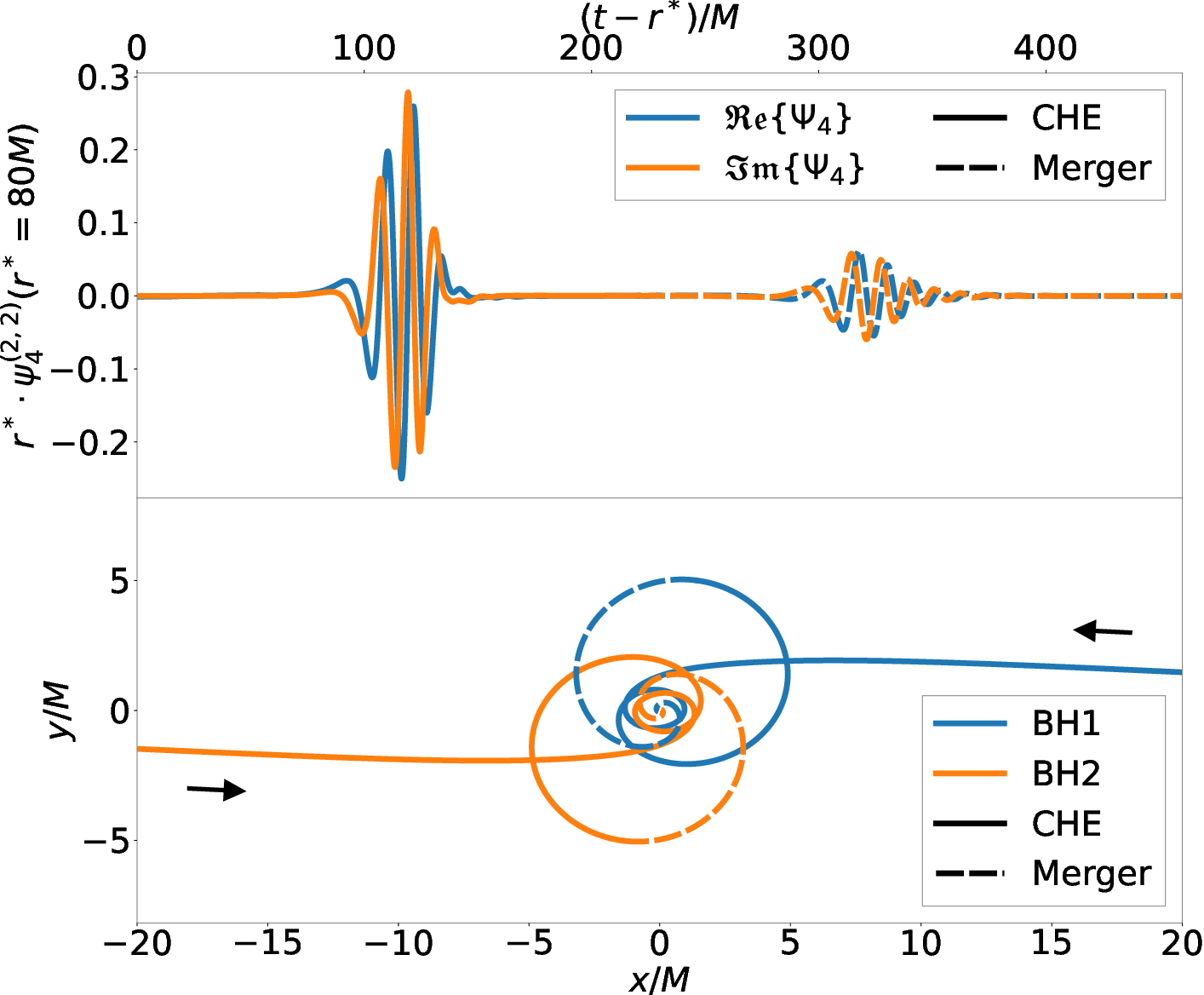
Figure 1: Evolution of the $(2,2)$ multipole of the Weyl scalar at $r^*=80M$ (upper panel) and BH trajectories (lower panel) for $p/M=0.49$, $\theta=2.85^\circ$.

The amplitude and structure of the GW emissions depend sensitively on the initial momenta and incidence angles. Higher $p/M$ leads to more energetic CHEs and stronger GW bursts, while larger $\theta$ increases the likelihood of capture for slower-moving BHs.

Evolution of Black Hole Properties

The time evolution of the dimensionless spin parameter $\chi$, ADM mass, and irreducible mass is tracked for both progenitor BHs and the final remnant.

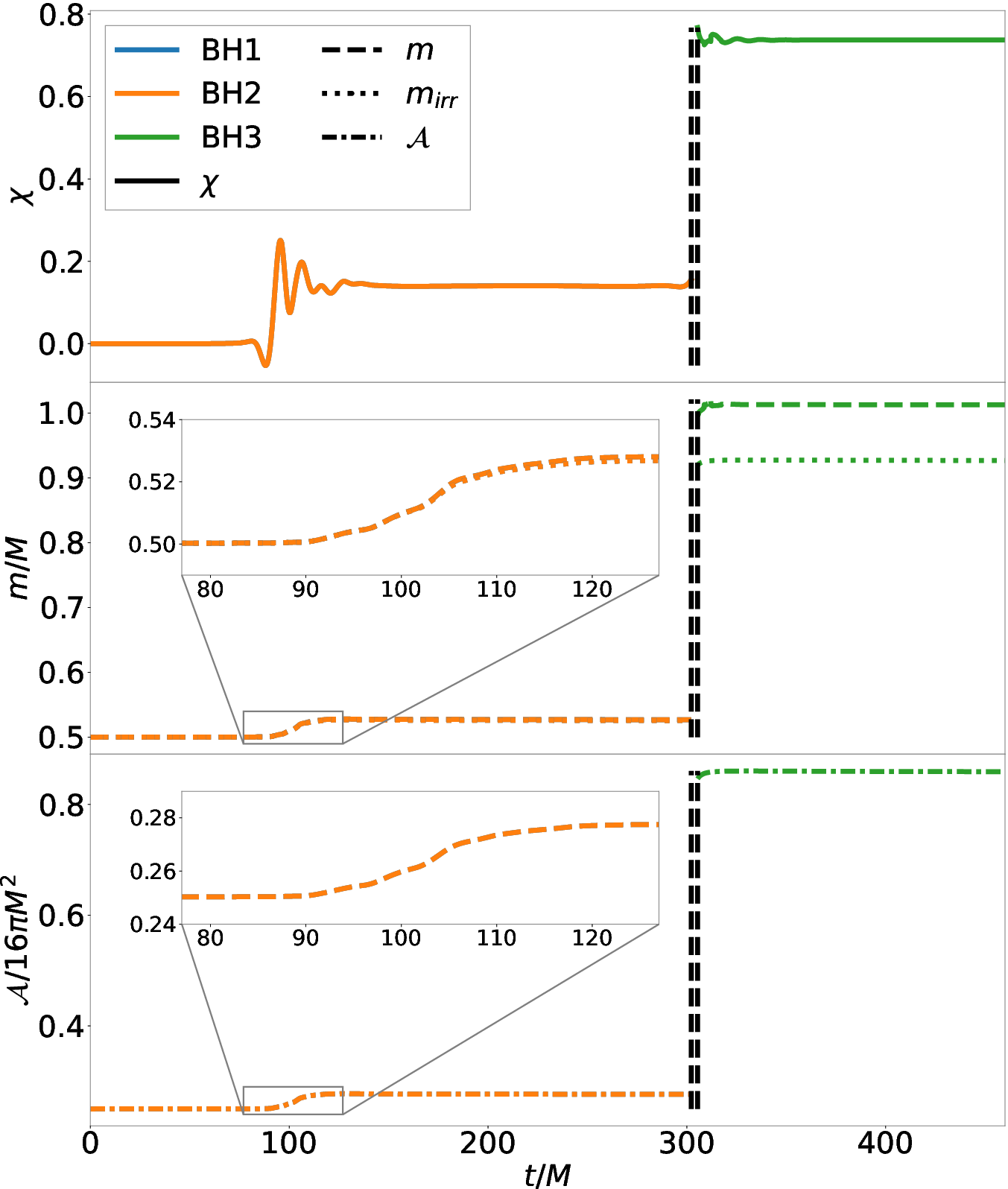
Figure 2: Time evolution of spin $\chi$ (upper), ADM and irreducible masses (middle), and horizon area (lower) for $p/M=0.49$, $\theta=2.85^\circ$.

During the CHE, significant spin-up ($\Delta\chi \sim 0.14$) and mass increase ($\sim 5\%$) are observed, attributed to GW absorption. The final remnant mass can exceed the initial total mass due to horizon absorption, consistent with Hawking's area law. The area of the final BH is always larger than the sum of the progenitors.

Analytical Modeling of the Weyl Scalar

The GW signal is modeled using a two-stage fit:

• CHE emission: Sin-Gaussian function

$$\Psi_4^{\text{CHE}} = A_{\text{CHE}} \sin[\omega_{\text{CHE}} (t - t_0^{\text{CHE}}) + \phi_{\text{CHE}}] e^{-(t - t_0^{\text{CHE}})^2 / 2\sigma_{\text{CHE}}^2}$$

• Merger and ringdown: Sin-Gaussian for merger, damped sinusoid for ringdown

$$\Psi_4^{\mathcal{R}} = A^{\mathcal{R}} \sin[\omega^{\mathcal{R}} (t - t_a) + \phi^{\mathcal{R}}] e^{-(t - t_a)/\tau^{\mathcal{R}}}$$

Joint fits are performed for the real and imaginary parts, enforcing a $\pi/2$ phase shift and common frequency. The model accurately reproduces the NR waveforms, especially for the ringdown phase.

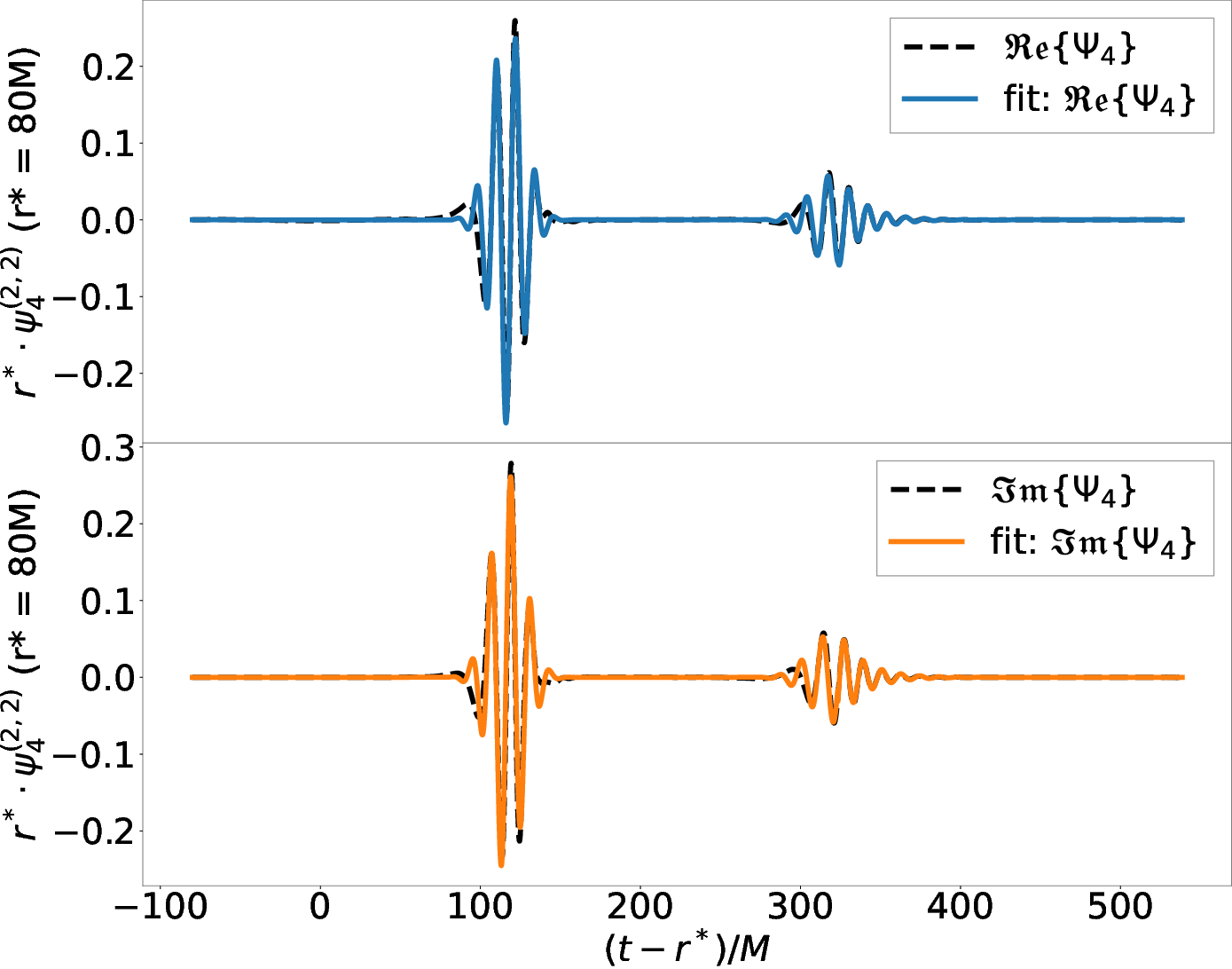
Figure 3: Fits of real (blue) and imaginary (orange) parts of $\Psi_4$ compared to NR data (black dashed) for $p/M=0.49$, $\theta=2.85^\circ$.

Time-Interval and Threshold Angle Analysis

The temporal separation $\Delta t = t_0^{\text{M}} - t_0^{\text{CHE}}$ between the CHE and merger peaks diverges as the incidence angle approaches a critical threshold $\theta_0$, marking the transition from scattering to capture. This behavior is well described by

$\Delta t/M = \frac{A}{1 - \theta/\theta_0} + B$

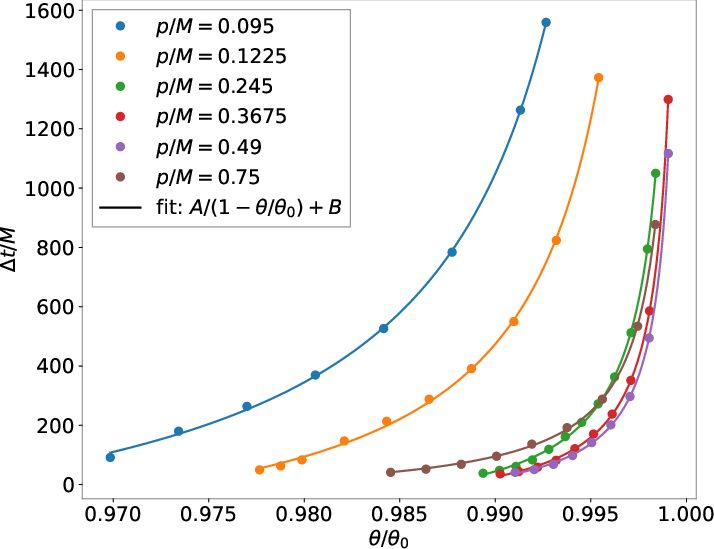
Figure 4: Time intervals $\Delta t$ between GW emission peaks as a function of normalized incidence angle $\theta/\theta_0$.

The threshold angle $\theta_0$ decreases with increasing $p/M$ for non-relativistic cases, but increases again at high $p/M$, possibly due to enhanced spin-spin coupling.

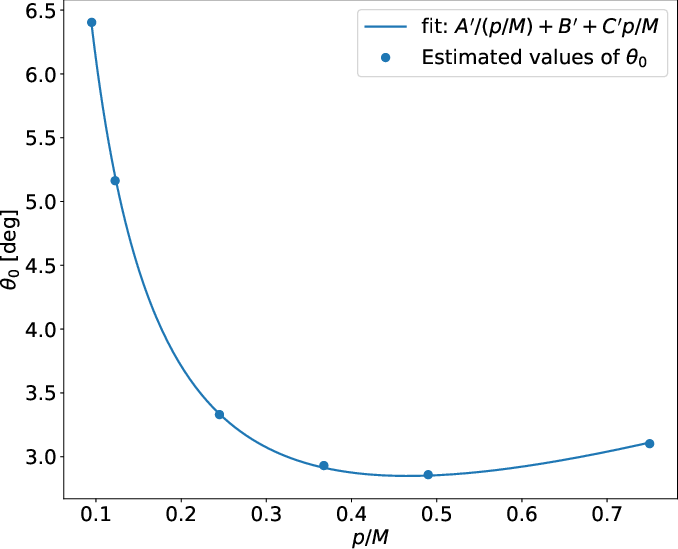
Figure 5: Estimated threshold angles $\theta_0$ as a function of $p/M$.

Parameter Trends and Phenomenological Waveform Model

The fitted parameters for the CHE emission (amplitude, frequency, width, phase) exhibit linear or exponential trends with $\theta/\theta_0$, enabling construction of a compact phenomenological waveform model.

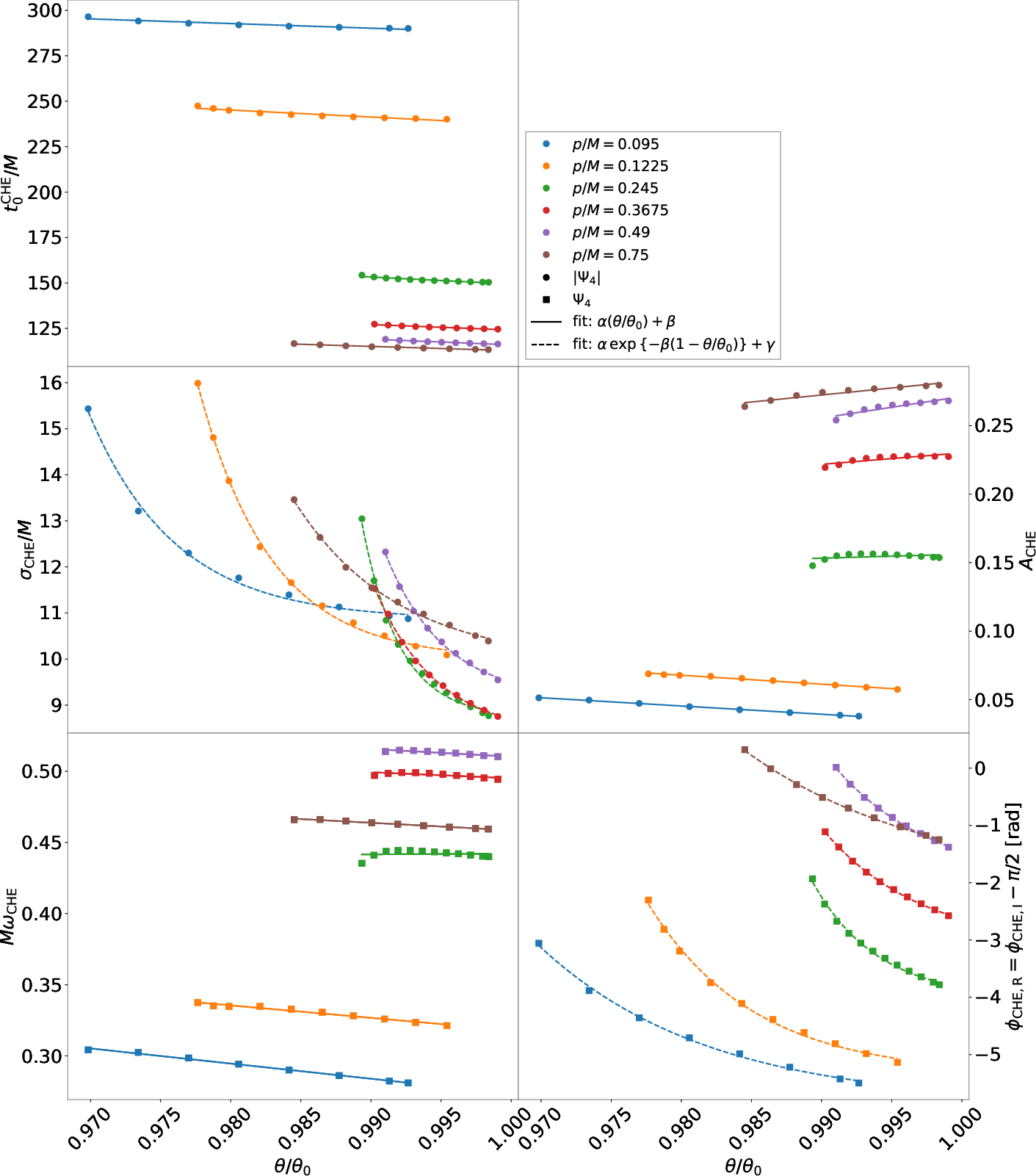
Figure 6: Estimated CHE parameters as functions of normalized incidence angle for all $p/M$ scenarios.

For the merger and ringdown phases, parameter trends are less regular, with clustering and mild oscillations, especially for phase shifts. The amplitude ratio $A_{\rm M}/A_{\rm CHE}$ varies from unity to $\sim 0.2$ for highly relativistic cases.

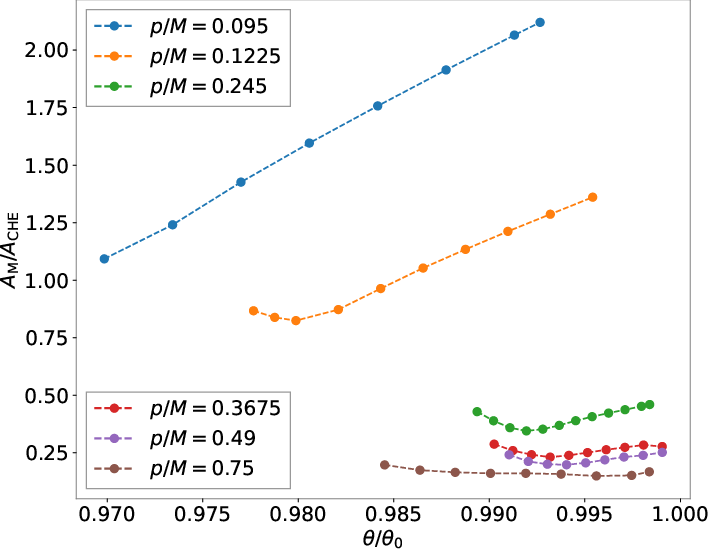
Figure 7: Ratio of merger to CHE amplitudes $A_{\rm M}/A_{\rm CHE}$ across scenarios.

Final Black Hole Properties and Radiated Energy

The final BH spin $\chi_{\rm f}$, extractable energy $E_{\text{extractable}}$, ADM mass $M_{\rm f}$, irreducible mass $M_{\rm f,irr}$, radiated mass $M_{\rm rad}$, and area increase are systematically analyzed.

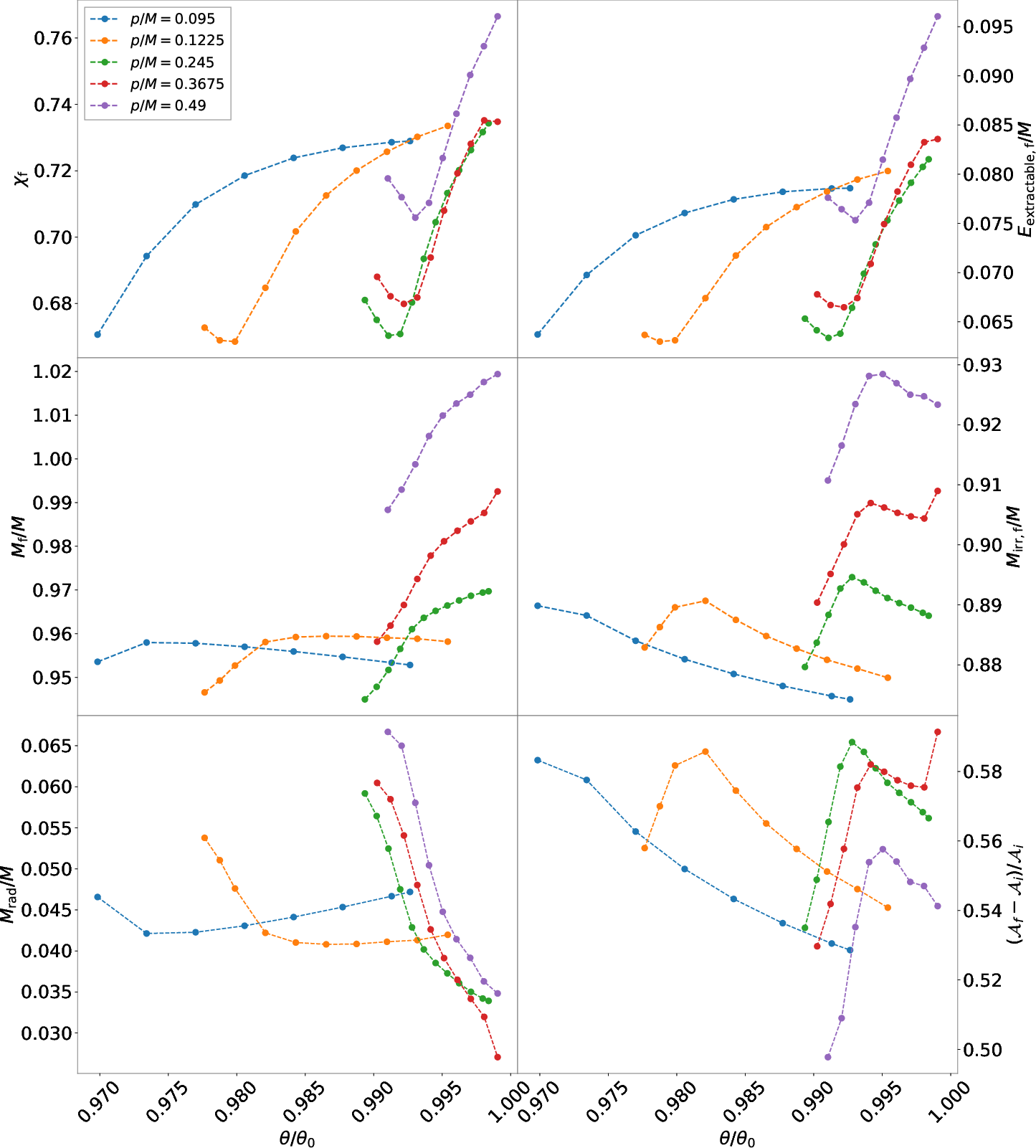
Figure 8: Final BH spin, extractable energy, mass, irreducible mass, radiated mass, and area difference as functions of $\theta/\theta_0$.

Key findings include:

• $\chi_{\rm f} \in [0.67, 0.77]$, with non-monotonic dependence on $\theta/\theta_0$.
• $E_{\text{extractable}}$ correlates linearly with $\chi_{\rm f}$.
• $M_{\rm rad}$ ranges from $3\%$ to $6\%$ of the initial mass, consistent with observed GW events.
• All simulations satisfy Hawking's area law.

Implications and Future Directions

The results provide a robust framework for modeling DC waveforms and interpreting GW signals from non-circular, high-eccentricity BH mergers. The analytical model for $\Psi_4$ enables efficient parameter estimation and can be incorporated into GW data analysis pipelines. The observed trends in BH properties and GW emission inform the development of surrogate models and N-body simulations of dense BH clusters.

The paper highlights the importance of horizon absorption, spin induction, and relativistic effects in DC events. Future work should extend the analysis to spinning and unequal-mass binaries, refine the merger-ringdown transition modeling, and explore the detectability of DCs with next-generation GW detectors. The methodology is also applicable to neutron star encounters and other compact object mergers.

Conclusion

This paper presents a comprehensive NR investigation of dynamical capture events between equal-mass, non-spinning BHs, elucidating the GW emission morphology, BH property evolution, and analytical modeling of the Weyl scalar. The findings establish clear parameter dependencies, validate physical laws (e.g., Hawking's area theorem), and provide a foundation for future waveform modeling and GW data analysis in the context of DCs and CHEs. The results are expected to play a significant role in the interpretation of GW signals from dense astrophysical environments as detector sensitivities improve.