Sharp Transitions for Subsystem Complexity (2510.18832v1)

Abstract: The circuit complexity of time-evolved pure quantum states grows linearly in time for an exponentially long time. This behavior has been proven in certain models, is conjectured to hold for generic quantum many-body systems, and is believed to be dual to the long-time growth of black hole interiors in AdS/CFT. Achieving a similar understanding for mixed states remains an important problem. In this work, we study the circuit complexity of time-evolved subsystems of pure quantum states. We find that for greater-than-half subsystem sizes, the complexity grows linearly in time for an exponentially long time, similarly to that of the full state. However, for less-than-half subsystem sizes, the complexity rises and then falls, returning to low complexity as the subsystem equilibrates. Notably, the transition between these two regimes occurs sharply at half system size. We use holographic duality to map out this picture of subsystem complexity dynamics and rigorously prove the existence of the sharp transition in random quantum circuits. Furthermore, we use holography to predict features of complexity growth at finite temperature that lie beyond the reach of techniques based on random quantum circuits. In particular, at finite temperature, we argue for an additional sharp transition at a critical less-than-half subsystem size. Below this critical value, the subsystem complexity saturates nearly instantaneously rather than exhibiting a rise and fall. This novel phenomenon, as well as an analogous transition above half system size, provides a target for future studies based on rigorous methods.

• The paper demonstrates that subsystem complexity undergoes sharp transitions at half system size and temperature-dependent critical fractions using holographic and random quantum circuit approaches.
• It employs analytical scaling laws and numerical simulations to show linear growth for larger subsystems and rapid saturation for smaller ones.
• The findings bridge quantum information theory and holography, highlighting complexity as a sensitive probe for many-body dynamics and black hole physics.

Sharp Transitions in Subsystem Complexity: Holographic and Quantum Circuit Perspectives

Overview and Motivation

This work investigates the dynamics of quantum circuit complexity for subsystems of pure quantum states, focusing on the emergence of sharp transitions as a function of subsystem size and temperature. The paper is motivated by analogies between black hole interior growth in AdS/CFT and the linear-in-time growth of circuit complexity in chaotic quantum many-body systems. While the complexity of global pure states is known to grow linearly for exponentially long times, the behavior for mixed states and subsystems has remained less understood. The authors employ both holographic duality and rigorous random quantum circuit (RQC) analysis to elucidate universal features of subsystem complexity dynamics, including the identification of sharp transitions at half system size and at a temperature-dependent critical fraction.

Holographic Construction and Subsystem Complexity

The holographic approach leverages the AdS/CFT correspondence, where the complexity of a boundary quantum state is dual to geometric quantities in the bulk, such as the volume of the Einstein-Rosen (ER) bridge or the action of certain spacetime regions. For subsystems, the relevant bulk region is the entanglement wedge, bounded by the Ryu-Takayanagi (RT) surface. The time evolution of subsystem complexity is governed by transitions between connected and disconnected extremal surfaces, known as the Hartman-Maldacena (HM) transition.

For subsystems larger than half the total system, the entanglement wedge includes the growing ER bridge, leading to exponentially long linear complexity growth. For subsystems smaller than half, the wedge becomes disconnected, and complexity saturates rapidly. The transition at exactly half system size is sharp and robust, dictated by the topology of the entanglement wedge rather than the details of the complexity prescription.

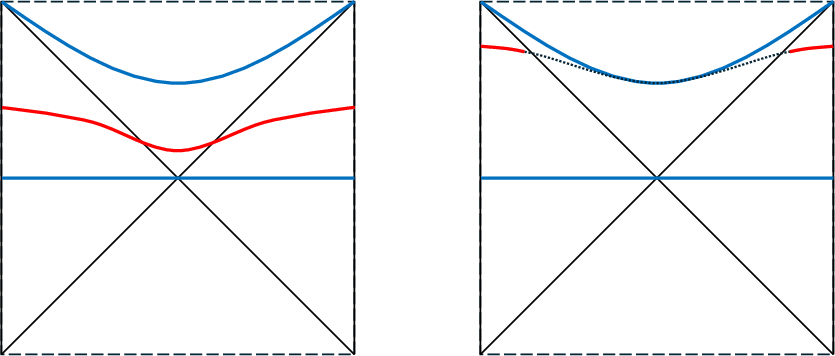
Figure 1: Hartman-Maldacena transition. Early-time connected extremal surface crosses the ER bridge; late-time disconnected surface terminates outside the horizon. Dominance exchanges at the thermalization time.

The analysis further reveals additional transitions at finite temperature. Below a critical subsystem fraction $p_\text{crit}$ (which decreases with temperature), complexity saturates almost instantaneously. Between $p_\text{crit}$ and $1/2$, complexity exhibits a rise and fall, saturating after a time that grows sublinearly with subsystem size. Above $1/2$, complexity grows linearly for exponentially long times, with discontinuous changes in growth rate and value at $1 - p_\text{crit}$.

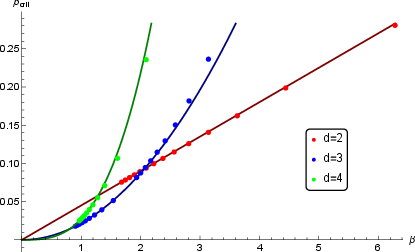
Figure 2: $p_\text{crit}$ as a function of temperature, indicating the critical subsystem fraction below which complexity saturates instantly.

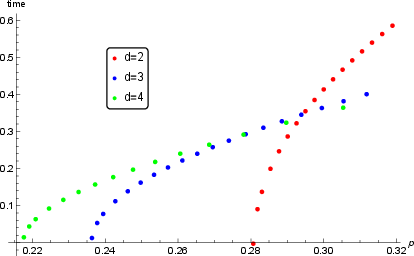
Figure 3: Saturation time versus subsystem fraction $p$ for black holes at the Hawking-Page threshold and $p < 1/2$.

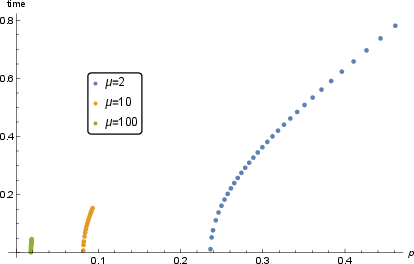
Figure 4: Saturation time versus subsystem size for $d = 3$, $\ell = 1$, and $\mu = 2, 10, 100$. Higher $\mu$ (temperature) yields smaller $p_\text{crit}$ and faster saturation.

Random Quantum Circuit Analysis

The authors rigorously analyze subsystem complexity in 1D RQCs, using both brickwork and patchwork architectures. The complexity of a mixed state is defined via purification, minimizing over all circuits that prepare a purification with polynomially many ancillas. For subsystems larger than half, complexity grows linearly in time for exponentially long times, mirroring the global state. For subsystems smaller than half, complexity rises and then falls, saturating to $O(n_A)$ (where $n_A$ is the subsystem size) after a time $O(n_A)$.

The transition at half system size is proven to be sharp: for $p < 1/2$, the reduced density matrix rapidly approaches the maximally mixed state, which has low complexity. For $p > 1/2$, the subsystem retains high complexity for exponentially long times. The analysis employs unitary $k$-design techniques to bound the complexity growth and saturation, with explicit dependence on circuit depth and subsystem size.

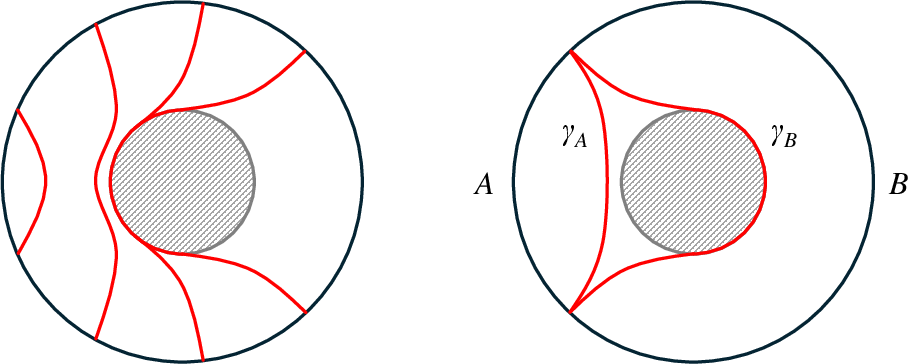
Figure 5: The one-sided BTZ black hole geometry, illustrating RT surfaces for various subregion sizes and their complements.

Analytical and Numerical Results

The paper provides both analytical scaling laws and detailed numerical results for the transition times and critical fractions. In the planar black hole limit, the saturation time for $p < 1/2$ scales as $p^{1/(d-1)}$, independent of the local qubit density. The critical fraction $p_\text{crit}$ scales as $(\beta/\ell)^{d-1}$, where $\beta$ is the inverse temperature and $\ell$ is the system size. Numerical solutions of the extremal surface equations confirm these scaling laws and reveal the dependence of $p_\text{crit}$ on temperature and spatial dimension.

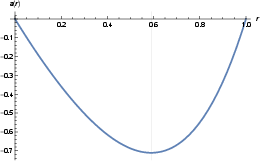
Figure 6: $a(r)$ for $r\in [0, r_h]$ with black hole parameters $d = 3$, $\ell = 1$, $\mu = 2$. $a(r)$ vanishes at $r = 0$ and $r = r_h = 1$; minimum at $r_m\approx 0.589755$.

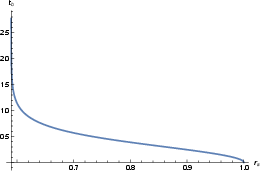
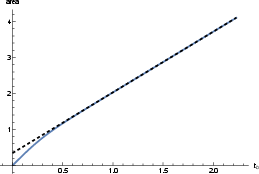
Figure 7: Properties of analytical solution with $\theta_0 = \pi/2$ and the same black hole parameters as in Figure 6.

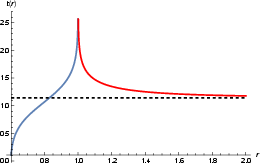
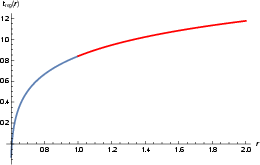
Figure 8: Example of an analytical solution for $r_s = 0.6$, with the same parameter values as in Figure 6.

Figure 9: Example of a static solution for $\theta(r)$ with $r_0 = r_h + 0.005 = 1.005$ and asymptotic value $\theta_0\approx 1.77315$. Inset shows non-monotonicity near the plateau.

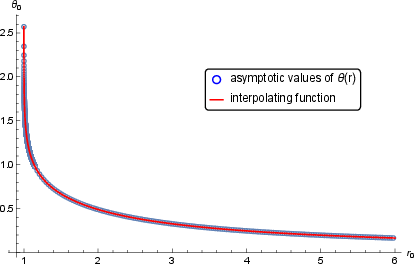
Figure 10: $\theta_0$ versus $r_0$, computed via numerical solutions for $\theta(r)$. $r_0$ ranges from slightly above $r_h$ to $r_h + 5$; $\theta_0$ ranges from $\pi$ to $0$ as $r_0$ increases.

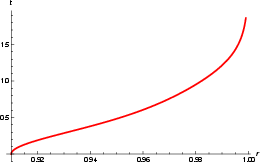
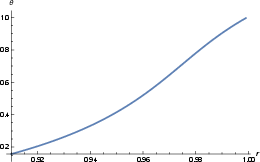
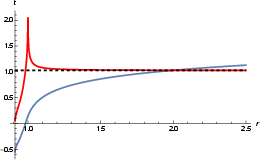
Figure 11: Inner solution for $t(r)$, illustrating the behavior near the horizon.

Implications and Future Directions

The identification of sharp transitions in subsystem complexity has significant implications for both quantum information theory and holographic duality. The results suggest that complexity is a more sensitive probe of many-body dynamics and thermalization than entanglement entropy, capturing features invisible to entropy-based measures. The existence of a temperature-dependent critical fraction $p_\text{crit}$ provides a new target for rigorous studies in systems with conserved quantities or finite temperature.

The work raises several open questions:

• Can similar transitions be established for time-independent Hamiltonian evolution, beyond RQCs?
• What is the behavior of subsystem complexity in higher-dimensional or non-local circuit architectures?
• How do other complexity measures (e.g., Krylov complexity, channel complexity) relate to the observed transitions?
• Can the discontinuous time transitions (the "sawtooth" profile) be made rigorous in the large local dimension limit?

The results also inform the modeling of black hole dynamics and scrambling, suggesting that RQCs capture universal features of complexity growth, but may require refinement to fully match holographic predictions, especially at finite temperature and in the presence of conserved quantities.

Conclusion

This paper establishes the existence of sharp transitions in the dynamics of subsystem complexity, both in holographic models and in random quantum circuits. The transition at half system size is proven to be sharp and universal, with additional temperature-dependent transitions predicted by holography. The rigorous analysis of RQCs confirms the qualitative and quantitative features suggested by the gravitational dual, providing a bridge between quantum information theory and quantum gravity. These findings advance the understanding of complexity as a fundamental property of quantum many-body systems and open new avenues for research in both fields.