Actor-Free Continuous Control via Structurally Maximizable Q-Functions (2510.18828v1)
Abstract: Value-based algorithms are a cornerstone of off-policy reinforcement learning due to their simplicity and training stability. However, their use has traditionally been restricted to discrete action spaces, as they rely on estimating Q-values for individual state-action pairs. In continuous action spaces, evaluating the Q-value over the entire action space becomes computationally infeasible. To address this, actor-critic methods are typically employed, where a critic is trained on off-policy data to estimate Q-values, and an actor is trained to maximize the critic's output. Despite their popularity, these methods often suffer from instability during training. In this work, we propose a purely value-based framework for continuous control that revisits structural maximization of Q-functions, introducing a set of key architectural and algorithmic choices to enable efficient and stable learning. We evaluate the proposed actor-free Q-learning approach on a range of standard simulation tasks, demonstrating performance and sample efficiency on par with state-of-the-art baselines, without the cost of learning a separate actor. Particularly, in environments with constrained action spaces, where the value functions are typically non-smooth, our method with structural maximization outperforms traditional actor-critic methods with gradient-based maximization. We have released our code at https://github.com/USC-Lira/Q3C.
Summary
- The paper presents Q3C, a value-based RL algorithm that removes the actor network by structurally maximizing Q-functions using control-point interpolation.
- It employs action-conditioned Q-value generation, relevance-based control-point filtering, and a decaying smoothing parameter to ensure stability and efficiency.
- Empirical results demonstrate that Q3C outperforms traditional actor-critic methods, particularly in constrained and non-convex action spaces.
Actor-Free Continuous Control via Structurally Maximizable Q-Functions: Q3C
Introduction
This paper presents Q3C, a value-based reinforcement learning algorithm for continuous control that obviates the need for an explicit actor network by leveraging a structurally maximizable Q-function. The approach is motivated by the limitations of actor-critic methods in continuous domains, particularly their instability and susceptibility to local optima in non-convex or constrained action spaces. Q3C revisits the wire-fitting control-point framework, introducing architectural and algorithmic innovations that enable competitive performance with state-of-the-art actor-critic methods, and superior robustness in environments with complex Q-value landscapes.
Q3C Architecture and Algorithmic Innovations
Q3C models the Q-function using a set of control-points, each representing a candidate action and its associated Q-value. The Q-value for any action is computed via inverse-distance weighted interpolation over these control-points, guaranteeing that the global maximum is attained at one of the control-points. This property enables direct maximization in continuous action spaces without gradient ascent or sampling-based optimization.
Figure 1: Q3C Architecture consists of a control-point generator, Q-estimator, and wire-fitting interpolator for inverse-distance weighted Q-value estimation.
Key architectural components include:
- Action-Conditioned Q-Value Generation: The Q-value for each control-point is computed by a shared Q-estimator conditioned on the control-point action, ensuring consistency and stabilizing learning.
- Relevance-Based Control-Point Filtering: Only the top- control-points (by proximity or relevance) are used for interpolation, sharpening the local value landscape and improving sample efficiency.
- Control-Point Diversity Loss: A pairwise separation loss encourages control-points to be well-dispersed in the action space, enhancing expressivity and robustness.
- Scale-Aware Normalization: Q-values and action distances are normalized to mitigate the effects of varying reward scales and action ranges across environments.
- Decaying Smoothing Parameter: An exponentially decaying smoothing coefficient in the interpolation kernel yields greater training stability than learned or fixed smoothing.
The Q3C update follows a TD3-style framework, employing twin Q-networks, target networks, and Gaussian exploration noise, but replaces the actor network with direct maximization over control-points.
Theoretical Properties
The wire-fitting interpolator used in Q3C is shown to be a universal approximator for continuous Q-functions over compact action sets. For any continuous and , there exists a finite set of control-points such that the interpolated Q-function approximates to within uniformly. This ensures that Q3C retains the representational power of deep Q-networks while enabling efficient maximization.
Empirical Evaluation
Standard Environments
Q3C is evaluated on a suite of continuous control tasks from Gymnasium, including Pendulum, Swimmer, Hopper, BipedalWalker, Walker2d, HalfCheetah, and Ant. Results demonstrate that Q3C matches or exceeds the performance of TD3 in most environments, and consistently outperforms other actor-free baselines such as vanilla wire-fitting, NAF, and RBF-DQN.
Figure 2: Comparison against TD3, SAC, and PPO on Standard Environments.
Q3C's performance is robust across a range of hyperparameters and network sizes, with only marginal increases in memory footprint compared to TD3. The parallelized evaluation of control-points enables scalability to high-dimensional action spaces.
Restricted Environments
In environments with constrained action spaces (e.g., actions restricted to unions of hyperspheres), Q3C demonstrates clear advantages over actor-critic methods. The induced non-convexity and discontinuities in the Q-function landscape cause gradient-based actors to converge to suboptimal local maxima. Q3C, by direct maximization over control-points, consistently achieves higher rewards and greater stability.
Figure 3: Q3C consistently outperforms TD3, RBF-DQN, and Wire-Fitting in restricted environments, converging at higher reward and stability.
Figure 4: Comparison against TD3, SAC, and PPO on Restricted Environments.
Visualization of learned Q-functions reveals that Q3C is able to model complex, multimodal landscapes, whereas TD3 and other baselines are often trapped in local optima.
Figure 5: The learned Q-functions for TD3 and Q3C are more complex and multimodal in restricted environments, with Q3C better capturing global optima.
Ablation Studies
Ablation experiments validate the necessity of each Q3C component. Removal of action-conditioned Q-value generation, control-point diversity, relevance filtering, or normalization leads to significant drops in performance and stability. The full Q3C model consistently outperforms all ablated variants and vanilla wire-fitting.
Figure 6: Ablations of Q3C show that all components are necessary for optimal performance; the combined model visibly outperforms ablations.
Figure 7: Decaying smoothing yields more stable learning than learned or fixed smoothing parameters.
Figure 8: Q3C is robust across different numbers of control-points and top- filtering configurations.
Implementation Considerations
Q3C is implemented using PyTorch, with architectural choices mirroring TD3 for fair comparison. The control-point generator and Q-estimator are parameterized by neural networks, with parallelized evaluation for scalability. Hyperparameters such as the number of control-points, separation loss weight, and smoothing schedule are tuned per environment. Memory usage scales favorably compared to actor-critic methods, especially in large models, due to the absence of an actor network.
Wall-clock time comparisons indicate that Q3C achieves target rewards faster than SAC and PPO in restricted environments, with competitive runtime in standard tasks. The interpolation mechanism introduces some overhead, but this is offset by the removal of the actor network.
Practical and Theoretical Implications
Q3C demonstrates that pure value-based RL is viable in continuous domains, provided the Q-function is structurally maximizable. This approach is particularly advantageous in safety-critical or constrained environments, where policy-gradient methods are prone to local optima and instability. The control-point framework offers a flexible foundation for further enhancements, including improved exploration strategies, prioritized replay, and adaptation to offline RL.
Theoretically, Q3C bridges the gap between discrete and continuous value-based RL, showing that direct maximization is possible without restrictive function classes (e.g., quadratic or convex Q-functions). The universal approximation property ensures applicability to a wide range of tasks.
Future Directions
Potential avenues for future research include:
- Integrating advanced exploration schemes (e.g., Boltzmann over control-point values) to improve sample efficiency.
- Extending Q3C to stochastic policies and entropy-regularized objectives.
- Adapting the control-point architecture for offline RL, leveraging its interpolation constraints to mitigate overestimation.
- Optimizing the interpolation mechanism for large-scale deployment and real-time control.
- Investigating hybrid architectures that combine Q3C with actor-critic enhancements (e.g., batch normalization, -step returns).
Conclusion
Q3C introduces a robust, actor-free framework for continuous control in reinforcement learning, leveraging structurally maximizable Q-functions via control-point interpolation. The method matches or surpasses state-of-the-art actor-critic algorithms in standard benchmarks and exhibits superior performance in environments with complex or constrained action spaces. Ablation studies confirm the necessity of each architectural innovation, and theoretical analysis guarantees universal approximation. Q3C provides a promising foundation for future research in scalable, stable, and expressive value-based RL for continuous domains.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper introduces a new way to train AI agents to make good continuous decisions (like how much to turn a steering wheel or how hard to push a joystick). The method is called Q3C. Its goal is to keep things simple and stable by using only one “critic” network that scores actions, instead of using both an “actor” (which picks actions) and a “critic” (which scores them). The trick is to design the critic so it’s easy to find the best action directly, even when actions aren’t just a few buttons but can be any number on a continuous scale.
Big questions the researchers asked
The authors aimed to answer:
- Can we control robots or agents with continuous actions without needing a separate “actor” network?
- Can we make choosing the best action fast and reliable, even when the action space is complicated or has “unsafe” regions?
- Will this simpler, actor-free method perform as well as popular actor-critic methods (like TD3 or SAC), and even better in hard, constrained settings?
How did they try to answer them?
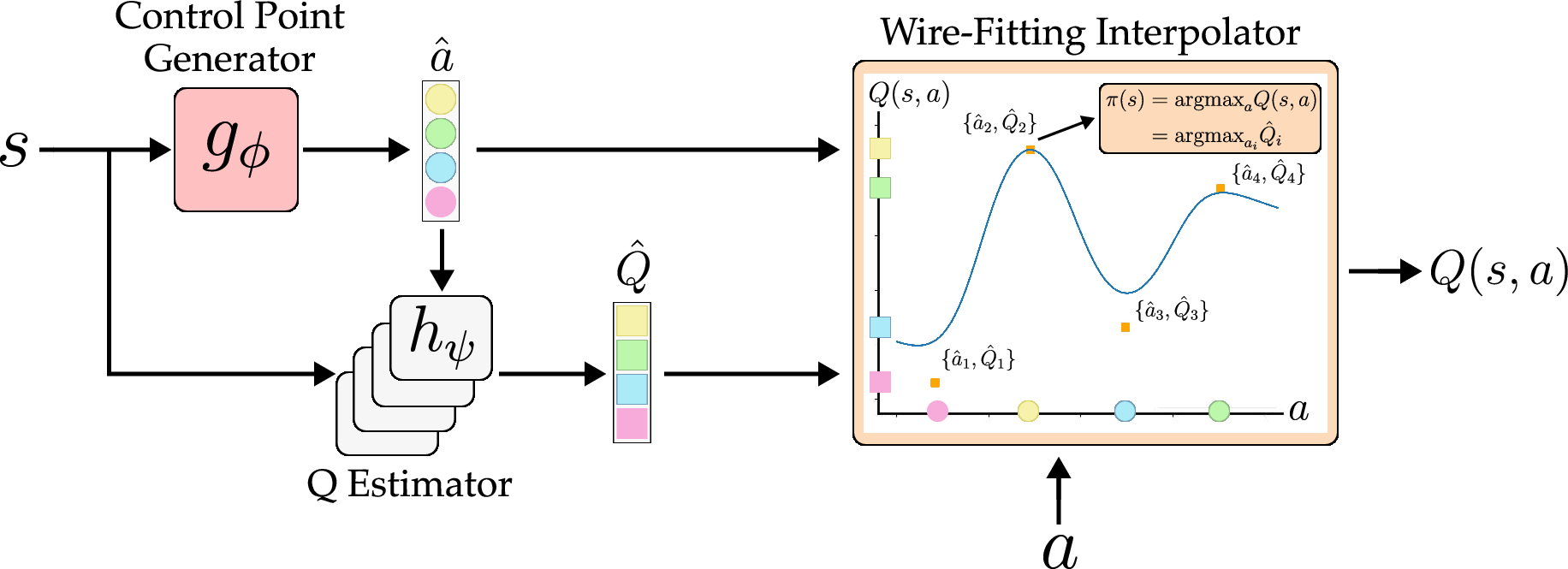
Think of the agent’s job as climbing a “score landscape” where every action at a given state has a score (called a Q-value). In continuous spaces, there are infinitely many actions, so finding the highest point is tricky. Q3C makes this easier with a design called “structural maximization,” which guarantees the top score is at one of a small set of special actions the network proposes.
The simple idea: “control-points”
- Imagine the agent lays down a handful of “checkpoints” (control-points) in the action space—candidate actions it thinks might be good.
- For each checkpoint, the network also predicts a score (its Q-value).
- Because of how Q3C is built, the highest score is guaranteed to be at one of these checkpoints. So to pick the best action, you just pick the checkpoint with the highest score.
This avoids having to climb the entire landscape with gradients (which can get stuck on local hills) or to sample tons of actions randomly (which can be slow and noisy).
How the system learns and stays stable
The authors found several smart tweaks are needed to make this “checkpoints” idea work well in real tasks:
- Action-conditioned scoring: The network first proposes checkpoint actions, then uses another part of the network to score those exact actions. This keeps scores consistent and reduces confusion.
- Top-k filtering: When evaluating a particular action, Q3C focuses on only the nearest few checkpoints (like listening to the closest voices), which sharpens local learning and avoids being distracted by far-away points.
- Diversity loss: Q3C encourages its checkpoints to spread out across the action space rather than clumping at the edges. This makes it more likely to cover useful parts of the space.
- Normalization: Since rewards (scores) can vary a lot across tasks, Q3C normalizes score differences inside its formula so the scoring is balanced and doesn’t get dominated by huge numbers.
- Built-in stabilizers: Q3C borrows proven stability tricks from TD3, like using two Q networks to avoid overestimating, target networks to make training targets steady, and a bit of noise to smooth action choice.
Overall, this design lets Q3C learn a Q-function whose maximum is easy to find—just pick the best checkpoint—without needing a separate actor to climb the landscape.
What did they find?
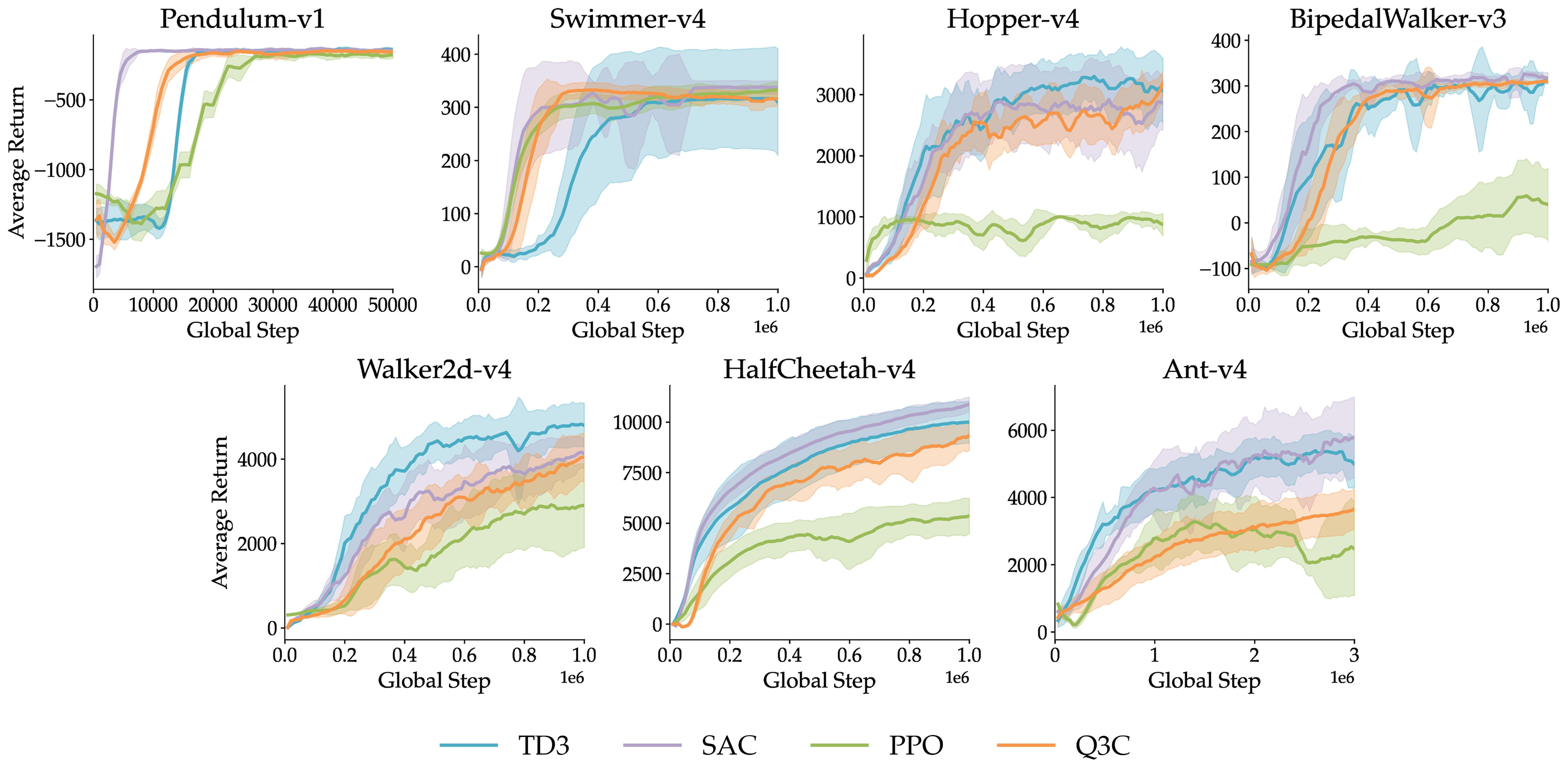
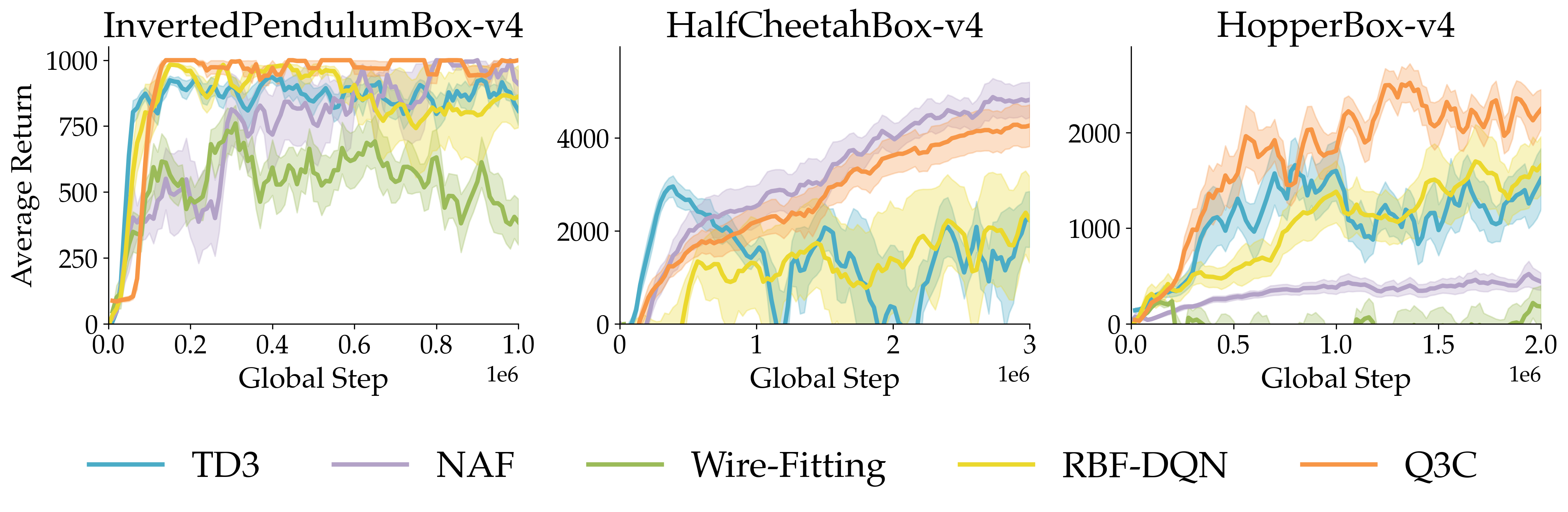
The team tested Q3C on common continuous-control tasks (like Pendulum, Hopper, Walker2d, HalfCheetah, Ant) and also on “restricted” environments where parts of the action space are invalid or unsafe, making the score landscape bumpy and tricky.
Main findings:
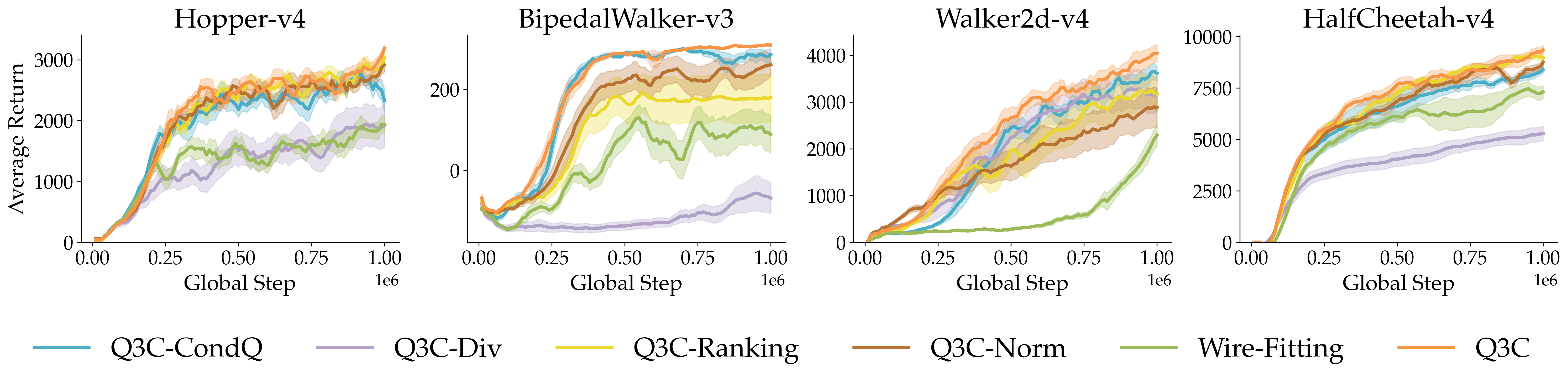
- On standard tasks, Q3C performs about as well as a strong actor-critic method (TD3), and better than other actor-free methods (like NAF, RBF-DQN, and vanilla wire-fitting).
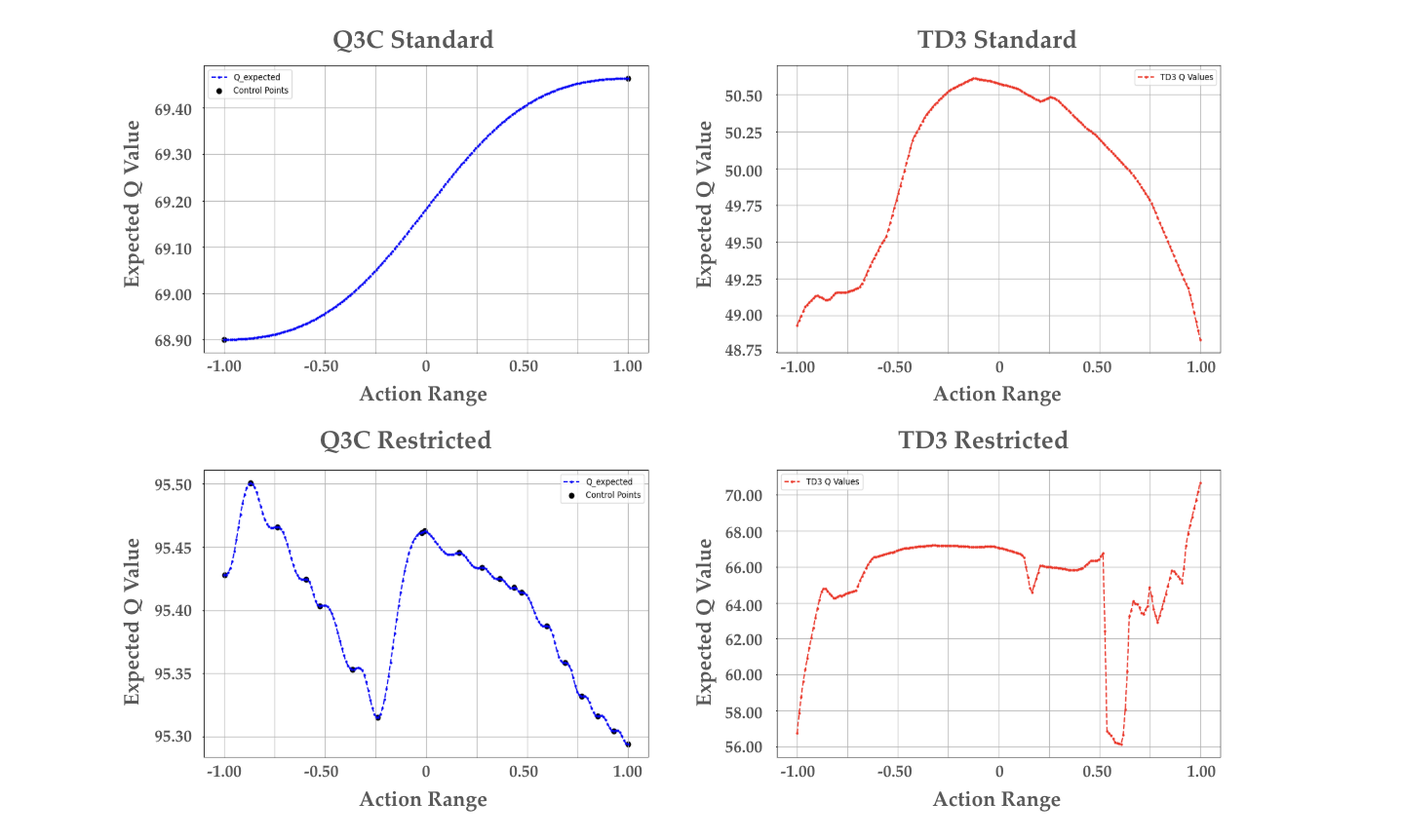
- On restricted tasks with constrained or non-smooth action spaces, Q3C often outperforms TD3. This makes sense because TD3’s actor uses gradient ascent and can get stuck on local hills, while Q3C can snap to the true maximum among its checkpoints.
- Ablation tests (removing parts of Q3C) showed each component helps. Without action-conditioned scoring, diversity, top-k filtering, or normalization, performance and stability drop. Together, they make the method robust.
Why it matters
This work shows you don’t always need a separate actor network to handle continuous actions. By designing the critic so the maximum is at one of a small set of learned checkpoints, action selection becomes simple, fast, and less fragile. This is especially useful in:
- Robotics with safety constraints (e.g., limited joint angles or safe torque ranges)
- Complex tasks where the best action might be hidden among many local optima
- Systems where simpler training (fewer networks and hyperparameters) improves reliability
Key takeaways
- Q3C is an “actor-free” continuous control method that picks the best action by choosing the highest-scoring checkpoint, avoiding gradient ascent over actions.
- It matches strong baselines on standard benchmarks and shines in constrained environments.
- Its success comes from combining a structurally maximizable Q-function with practical deep-learning tweaks: action-conditioned scoring, top-k filtering, checkpoint diversity, normalization, and stability tools from TD3.
- Future work could improve exploration, handle more tasks (like offline RL), and extend the approach to stochastic policies.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list highlights what remains missing, uncertain, or unexplored in the paper and points to concrete directions for future research.
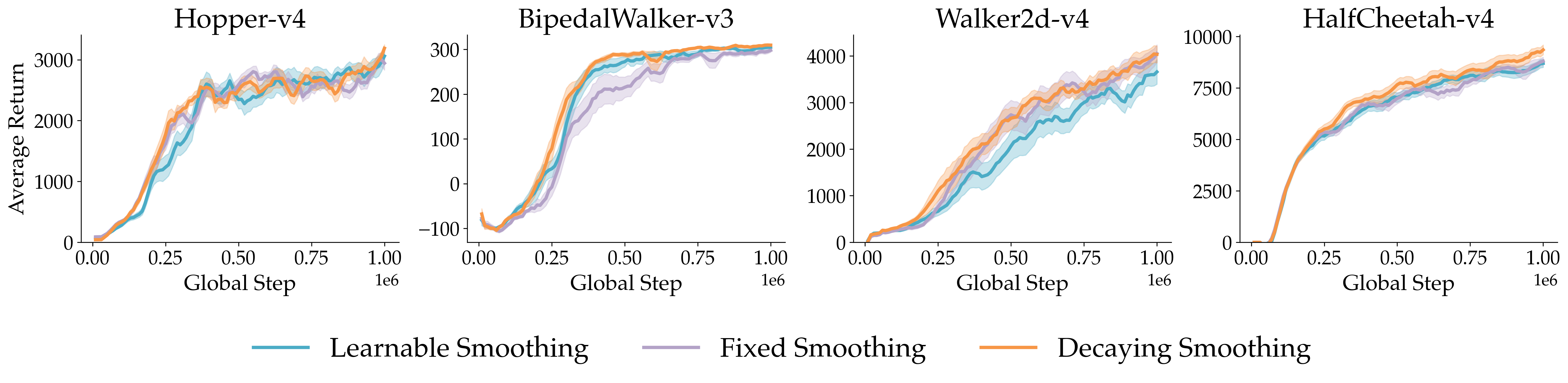
- Formal convergence guarantees: No theoretical analysis is provided for the convergence or stability of Q3C under its full set of modifications (action-conditioned Q-estimator, relevance-based top-k filtering, Q-value normalization in the kernel, smoothing schedules, target networks). Establishing contraction properties, error bounds, or conditions under which Q3C converges would make the method more rigorous.
- Maxima-at-control-points guarantee under modifications: The paper claims the Q-function’s maximum occurs at a control-point, but does not formally prove this property for the deep implementation with (i) hard top-k filtering, (ii) Q-value rescaling in the kernel, and (iii) exponentially decayed smoothing. A proof (or counterexample) for the implemented kernel would clarify when greedy action selection is exact.
- Kernel consistency and proof mismatch: The universal approximation proposition uses a kernel different from the main algorithm (e.g., distance vs squared distance; different smoothing term; min/max vs rescaled Q), and does not cover the practical adjustments (normalization, top-k). A unified theoretical treatment of the exact kernel used in Q3C is needed.
- Differentiability and gradient flow: The training relies on non-differentiable operations (argmax over control-point Q-values, min/max rescaling within each state, hard top-k selection). The paper does not address how gradients are handled (e.g., straight-through estimators, soft approximations), nor the impact on stability and bias. Analyzing and, if necessary, replacing discrete selections with differentiable relaxations would be valuable.
- Action-generator learning signal: It remains unclear how the control-point generator gφ receives robust gradients to place points near high-value actions when get_action(s) uses argmax over predicted Q_i and training targets come from replay actions, not from the greedy actions. A paper of the generator’s learning dynamics and explicit objectives for adaptive placement is missing.
- Adaptive control-point placement: The approach relies on a fixed number N and a diversity loss to spread control-points, but offers no mechanism to adaptively add/move/remove points to concentrate capacity near promising regions. Methods for adaptive control-point budgets (e.g., splitting/merging, curriculum placement, uncertainty-guided repositioning) are unexplored.
- Scalability to very high-dimensional action spaces: The paper tests up to moderate dimensions (e.g., Ant; mentions Adroit in appendix settings) but does not quantify how performance, N, k, and compute scale with action dimension (e.g., >20–50D). Benchmarks and complexity analyses on truly high-dimensional tasks are needed.
- Compute and memory cost vs actor-critic: Despite claiming the approach is “actor-free,” the architecture computes N control-point actions and their values per state. There is no measurement of training/inference time, GPU memory, and throughput compared to TD3/SAC. A comprehensive runtime and resource profile is missing.
- Sample efficiency quantification: The paper suggests Q3C is on par in sample efficiency, but provides only learning curves on selected tasks. A systematic analysis (e.g., area under curve, steps-to-threshold, performance vs number of environment steps) across diverse domains is not presented.
- Failure-mode analysis (e.g., Ant-v4): Q3C underperforms on Ant-v4, yet the paper does not diagnose why. Experiments isolating likely causes (action dimensionality, contact-rich dynamics, optimization landscape, control-point clustering) and targeted fixes would help.
- Exploration beyond Gaussian noise: Q3C inherits TD3-style Gaussian exploration; alternatives (Boltzmann over Q_i, UCB-style bonuses, CEM-style sampling over control-points, intrinsic motivation) are not evaluated. The impact of exploration strategies on performance and sample efficiency remains open.
- Robustness to reward scaling and normalization bias: Q-value rescaling to [0,1] inside the kernel alters the weight computation independent of the true Q scale; the bias this introduces into the Bellman targets and greedy action selection is not analyzed. Theoretical and empirical assessments of invariance and bias under different reward scales are missing.
- Overestimation/underestimation bias in wire-fitting: While twin Q-networks are used, the interaction between inverse-distance interpolation and double Q-learning is not studied. Quantifying estimation bias and devising controls (e.g., clipped interpolation, conservative updates) is an open task.
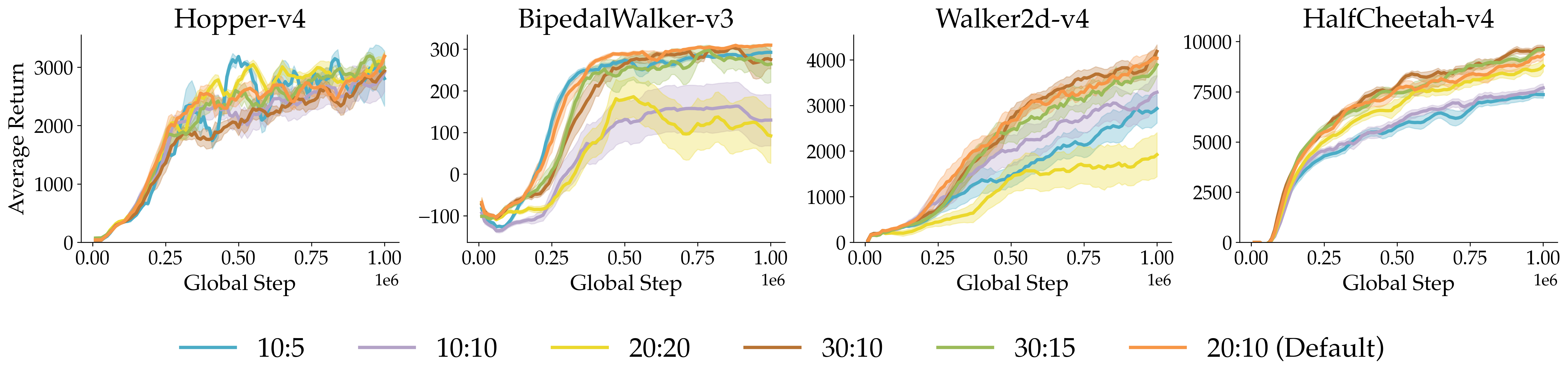
- Impact of top-k filtering choice: The hard relevance-based filtering (k ≪ N) improves stability, but there is no systematic paper relating k to local approximation error, convergence, or action selection fidelity. A principled way to set k (or learn it) is missing.
- Safety and constraints beyond synthetic hyperspheres: The constrained-action benchmarks are synthetic (invalid actions have no effect). Realistic safety constraints (state-dependent admissible sets, soft penalties, chance constraints) and methods to enforce them (projection layers, Lagrangian/dual formulations, constrained wire-fitting kernels) are not addressed.
- Partial observability and stochastic environments: The approach has not been tested with recurrent architectures, observation noise, or stochastic dynamics. Extending Q3C to POMDPs (e.g., LSTM/Transformer backbones) and evaluating robustness is an open question.
- Comparisons to stochastic actor-critic (SAC) in the main text: SAC comparisons are deferred to the appendix, and Q3C is deterministic. A thorough evaluation against entropy-regularized baselines and development of a “soft-Q3C” variant are missing.
- Action-space coverage vs concentration trade-off: The diversity loss spreads control-points, but may reduce concentration near true optima. An explicit mechanism to balance exploration (coverage) and exploitation (precision near peaks) and its effect on performance is not studied.
- Calibration and reliability of Q-values: The method leverages Q_i(s) primarily for ranking, yet it does not assess calibration (e.g., expected return vs predicted Q), nor propose calibration procedures (temperature scaling, monotonic constraints) to improve reliability.
- Sensitivity and auto-tuning of hyperparameters: Q3C involves several sensitive hyperparameters (N, k, λ for diversity, smoothing schedule c, learning-rate scheduler). A comprehensive sensitivity analysis and strategies for auto-tuning or meta-learning these parameters are absent.
- Kernel design alternatives: The inverse-distance kernel with Q-difference smoothing is fixed; potential alternatives (learned metric, Mahalanobis distance, anisotropic kernels, attention-based weights, local density-aware weighting) and their effect on accuracy and stability are unexplored.
- Handling non-differentiable ranking operations: The paper does not specify implementation details for backpropagation through top-k selection and min/max rescaling. Investigating soft top-k (e.g., differentiable sorting), Gumbel-top-k, or attention-based relevance weighting could improve trainability.
- Off-policy coverage and data distribution mismatch: Because control-points may cluster towards replayed actions, the method may struggle if the replay buffer undercovers optimal action regions. Techniques for coverage correction (e.g., pessimism, uncertainty-aware sampling, data-augmentation in action space) are not explored.
- Real-world validation: The approach is not evaluated on real robotic systems or safety-critical applications where constrained actions are common. Assessing latency, robustness to sensor noise, and failure rates in deployment would strengthen claims.
- Benchmarks beyond Gymnasium: Evaluating on harder, diverse suites (DM Control, Adroit, robotics manipulation, locomotion with contact-rich dynamics) would clarify generality and scalability.
- Offline RL extension: While mentioned as future work, Q3C’s compatibility with offline RL (e.g., conservative Q-learning, BCQ-style constraints, implicit regularization via interpolation) remains untested and untheorized.
- Global optimization guarantees: Structural maximization ensures the greedy action is a control-point, but there is no guarantee that learned control-points cover the global optimum. Methods to provide global optimality certificates or probabilistic guarantees based on coverage and N are missing.
Practical Applications
Below are practical, real-world applications derived from the paper’s findings and innovations in actor-free continuous control via structurally maximizable Q-functions (Q3C). Each item specifies sector(s), concrete use cases, potential tools/workflows, and key assumptions or dependencies affecting feasibility.
Immediate Applications
- Robotics: safer manipulation and locomotion under hard action constraints; deploy Q3C to pick-and-place, grasping, and mobile robots that must respect torque/velocity limits and contact-discontinuities; product/workflow: a single “critic-only” control stack that outputs control-points and selects the maximizing action (no actor), plus a control-point visualizer for debugging dispersion and local maxima. Assumptions/Dependencies: reliable simulation or safe RL infrastructure; action normalization to [-1,1]; moderate action dimensionality (N≈20–70 control-points); TD3-style exploration; safety shield or constraint projector when needed.
- Industrial process control: continuous setpoint tuning with non-smooth returns (e.g., chemical reactors, water treatment, printing lines) where standard policy gradients get stuck; workflow: retrofit Q3C into existing SCADA/MPC loops as an action-proposal layer that respects safety bounds. Assumptions/Dependencies: high-fidelity simulators or digital twins for off-policy training; robust reward scaling/normalization; supervisory safety constraints enforced downstream.
- Energy and buildings: HVAC control, battery charge/discharge scheduling, and microgrid dispatch under operational bounds; tool: Q3C-enabled controller with structural maximization that evaluates top-k control-points for fast action selection; integration with demand-response APIs. Assumptions/Dependencies: reliable sensor data; consistent reward shaping; validation under real-world disturbances.
- Networking/media: bitrate adaptation and congestion control with bounded actions (e.g., streaming QoE optimization); product: Q3C plugin for ABR controllers that produces stable actions amid discontinuities (link capacity changes). Assumptions/Dependencies: online/offline data logs; careful normalization to avoid reward-scale dominance in kernels.
- Automotive and e-mobility: throttle/brake/steering modulation within OEM safety envelopes for driver-assist or autonomous modules; workflow: actor-free RL module offering interpretable control-points for certification-friendly analysis. Assumptions/Dependencies: formal safety monitors; redundancy with classical controllers; extensive validation and ODD (operational design domain) scoping.
- Healthcare (operations): infusion pump flow control or lab automation (pipetting/centrifuge settings) with strict bounds; tool: Q3C controller for continuous parameters with non-convex performance profiles. Assumptions/Dependencies: clinical oversight; stringent testing; likely simulation or shadow-mode deployment before live use.
- Finance (ops-level tuning): market-making spread sizing or execution venue selection under bounded sizes and non-convex PnL surfaces; workflow: Q3C pilot in backtesting environments to probe local maxima issues. Assumptions/Dependencies: compliance gating; robust risk management; limited action dimensionality.
- Software engineering/ML ops: reinforcement-tuned autoscaling and continuous hyperparameter knobs (rate limits, caching TTLs) with discontinuous utility; product: Q3C “policy-free” tuner integrated into feature flags or canary pipelines. Assumptions/Dependencies: guardrails for rollback; offline replay buffers for safe training; normalized reward scales across services.
- Academia and teaching: reproducible RL labs that avoid actor-critic coupling and hyperparameter instability; tools: course modules using Q3C codebase, assignments to visualize control-point dispersion and top-k filtering. Assumptions/Dependencies: standard Gymnasium-like simulators; limited computational budgets; simple constraint setups.
- Policy and evaluation practice: benchmark expansions for constrained/non-convex action spaces in public RL evaluations; workflow: include “restricted action” tasks when assessing RL algorithms intended for safety-critical deployments. Assumptions/Dependencies: community consensus on benchmark definitions; open-source reference implementations (Q3C repo).
Long-Term Applications
- Safety-critical robotics and medical devices: surgical robots, radiation therapy alignment, and prosthetic/exoskeleton control where action-space constraints are strict and Q landscapes are non-convex; product: certification-oriented control stacks leveraging control-point maxima for explainability. Assumptions/Dependencies: extensive clinical trials; formal verification tooling around control-point maxima; integration with risk-aware learning and human oversight.
- Autonomous driving at scale: end-to-end or mid-level controllers (trajectory curvature, speed profiles) with hard constraints and discontinuities; workflow: Q3C fused with rule-based safety envelopes and scenario-level planners. Assumptions/Dependencies: large-scale data; domain randomization; strong safety cases; robustness under edge cases and high-dimensional action spaces.
- Grid-scale energy optimization: commitment and dispatch with multi-dimensional continuous decision vectors (battery fleets, distributed resources), with sharp discontinuities from market/physical constraints; tool: Q3C-based optimizer hybridized with MPC and economic dispatch solvers. Assumptions/Dependencies: interoperability with legacy systems; handling very high-dimensional actions (may require algorithmic scaling: adaptive N/k, hierarchical control-points); improved exploration/sample efficiency.
- Advanced manufacturing: robot swarms and flexible production lines with high-dimensional, continuous control under safety limits; product: “structurally maximizable” RL supervisor coordinating multi-agent actions. Assumptions/Dependencies: scaling Q3C to multi-agent settings; communication constraints; curriculum learning; stronger stability guarantees.
- Offline RL for constrained domains: use Q3C’s interpolation and structural maxima to mitigate overestimation in batch settings (healthcare, finance, industrial logs); tool: Q3C-Offline library with conservative Q updates and control-point uncertainty quantification. Assumptions/Dependencies: dataset coverage; off-policy corrections; confidence bounds over control-point values.
- Education and workforce tooling: interpretable RL dashboards that show control-points, their Q-values, and relevance filtering—supporting operator trust and training; product: “Control-Point Inspector” for audits, safety reviews, and debugging. Assumptions/Dependencies: UI/UX investment; data governance; alignment with organizational SOPs.
- Regulatory standards and certification: guidelines that favor actor-free or structurally maximizable RL in safety-critical domains due to better interpretability and explicit maxima properties; workflow: conformity assessment procedures referencing control-point distributions and top-k relevance. Assumptions/Dependencies: multi-stakeholder consensus; empirical evidence across sectors; harmonization with existing standards (ISO/IEC).
- Human-in-the-loop optimization: operators select among top-k control-points surfaced by the system (semi-automated control) in utilities, transport hubs, or hospital ops; product: decision support tools where RL proposes bounded actions and staff confirm/adapt. Assumptions/Dependencies: training and change management; guardrails; preference modeling and override workflows.
- High-dimensional dexterous manipulation: general-purpose hands and soft robots with many actuators; product: hierarchical Q3C that organizes control-points by subspaces and uses relevance filtering per subsystem. Assumptions/Dependencies: architectural advances for scalability; better exploration and sample efficiency; richer regularization (diversity, conditional Q heads).
- Research extensions: stochastic policies (soft-Q), prioritized replay, n-step returns, batchnorm-based critics; product: “Q3C+” research line combining DQN-style and actor-critic improvements for sample efficiency and robustness. Assumptions/Dependencies: empirical validation on diverse tasks (Ant, Adroit, real robots); ablation-heavy studies to isolate benefits; community adoption.
In all cases, feasibility hinges on key assumptions highlighted in the paper: normalized action spaces; appropriate reward scaling and kernel normalization; careful selection of control-point count N and top-k filtering; smoothing annealing; twin Q-networks and target networks for stability; and adequate exploration strategies. For high-stakes deployments, additional dependencies include formal safety monitors, thorough validation, and compliance-ready documentation of the structural maximization mechanism and its behavior under constraints.
Glossary
- Actor-critic methods: A reinforcement learning framework where a policy (actor) is trained alongside a value function (critic) to select actions in continuous spaces. "actor-critic methods are typically employed"
- Actor-free: A value-based approach that avoids learning a separate policy network and directly maximizes the Q-function to select actions. "actor-free Q-learning approach"
- Advantage function: The component of a value function that measures how much better an action is than the average at a state; often used as part of Q-function decompositions. "constructing the state-action advantage function in quadratic form"
- Bellman equation: A recursive relationship defining the optimal value of a decision problem by relating the value of a state-action pair to rewards and next-state values. "follows the Bellman equation,"
- Bellman residual: The difference between both sides of the Bellman equation, used as a minimization objective to improve value function estimates. "minimize the Bellman residual"
- Clipped double Q-learning: A technique that uses two Q-networks and clips their estimates to reduce overestimation bias and stabilize training. "clipped double Q-learning"
- Control-point generator: A network module that outputs representative actions (control-points) at a state, which are then evaluated by a Q-estimator. "a control-point generator estimates the representative control-point actions"
- Control-points: A finite set of learned actions with associated Q-values used in wire-fitting to make the Q-function structurally maximizable. "uses a finite number of control-points"
- Convex solver: An optimization routine that finds global optima for convex problems; here used for action selection under convex assumptions about the Q-function. "use a convex solver for action selection"
- Cross-entropy methods (CEM): Population-based optimization algorithms that iteratively update a sampling distribution to focus on high-performing solutions. "cross-entropy methods (CEM)"
- Deterministic policy gradient: A gradient-based method that directly optimizes a deterministic policy by ascending the critic’s output. "deterministic policy gradient algorithm"
- Distributional critics: Value function models that learn the full distribution of returns rather than just their expectation, improving robustness. "distributional critics"
- Entropy-regularized Q-function: A value function augmented with an entropy term to encourage exploration and stochasticity in policies. "maximizes an entropy-regularized Q-function."
- Greedy policy: A policy that selects actions with the highest estimated value at each state. "The greedy policy is optimal,"
- Inverse weighted interpolation: A smoothing interpolation method where weights decrease with distance and value differences, used in wire-fitting. "inverse weighted interpolation smoothed with "
- Markov Decision Process (MDP): A formalism for sequential decision-making with states, actions, rewards, and transition dynamics. "Markov Decision Process (MDP)"
- Mixed-integer programming: An optimization approach involving both integer and continuous variables; used in some RL formulations for action selection. "mixed-integer programming"
- Non-convex Q-function landscapes: Value function surfaces with multiple local maxima and complex geometry, challenging for gradient-based optimization. "non-convex Q-function landscapes"
- Off-policy: Learning from data generated by policies different from the one currently being optimized. "Off-policy actor-critic methods are widely employed"
- Partition of unity: A set of nonnegative weights that sum to one, used to interpret the interpolated value as a convex combination. "form a partition of unity"
- Prioritized replay buffers: Experience replay mechanisms that sample transitions with higher learning potential more frequently. "prioritized replay buffers"
- Radial basis function (RBF): A function centered at specific points used for interpolation; in RL, to approximate continuous Q-functions. "radial basis function (RBF) output layer"
- Replay buffer: A memory that stores past transitions for sampling during off-policy training. "Initialize replay buffer"
- Soft-Q function: A Q-function variant that incorporates entropy, enabling stochastic policies and improved exploration. "soft-Q function like SAC."
- Stochastic policy: A policy that outputs a distribution over actions rather than a single deterministic action. "learns a stochastic policy"
- Structural maximization: Designing the Q-function so its maximum can be found by evaluating a finite set of points rather than continuous optimization. "structural maximization of Q-functions"
- Structurally maximizable Q-function: A Q-function parameterization constructed so that the maximum lies at one of its learned control-points. "Structurally Maximizable Q-Functions"
- Target networks: Slowly updated copies of learning networks that provide stable targets for value updates. "target networks to make the learning targets stationary"
- Target policy smoothing: Adding noise to target actions during value estimation to improve generalization and stability. "target policy smoothing"
- Twin Q-networks: Using two separate Q-functions to reduce overestimation by taking the minimum of their predictions. "twin Q-networks"
- Universal approximation: The property that a function class (or parameterization) can approximate any continuous function to arbitrary accuracy. "preserves its universal approximation ability."
- Value-based algorithms: Methods that learn value functions (e.g., Q-functions) and derive policies via maximization, without directly parameterizing a policy. "Value-based algorithms are a cornerstone of off-policy reinforcement learning"
- Wire-fitting: A function approximation framework that interpolates values using control-points and inverse-distance weights. "wire-fitting, a general function approximation system"
- Wire-fitting interpolator: The specific interpolation formula in wire-fitting that computes the value at any action from control-point values and weights. "wire-fitting interpolator"
Collections
Sign up for free to add this paper to one or more collections.