STITCHER: Constrained Trajectory Planning in Complex Environments with Real-Time Motion Primitive Search (2510.14893v2)

Abstract: Autonomous high-speed navigation through large, complex environments requires real-time generation of agile trajectories that are dynamically feasible, collision-free, and satisfy state or actuator constraints. Modern trajectory planning techniques primarily use numerical optimization, as they enable the systematic computation of high-quality, expressive trajectories that satisfy various constraints. However, stringent requirements on computation time and the risk of numerical instability can limit the use of optimization-based planners in safety-critical scenarios. This work presents an optimization-free planning framework called STITCHER that stitches short trajectory segments together with graph search to compute long-range, expressive, and near-optimal trajectories in real-time. STITCHER outperforms modern optimization-based planners through our innovative planning architecture and several algorithmic developments that make real-time planning possible. Extensive simulation testing is performed to analyze the algorithmic components that make up STITCHER, along with a thorough comparison with two state-of-the-art optimization planners. Simulation tests show that safe trajectories can be created within a few milliseconds for paths that span the entirety of two 50 m x 50 m environments. Hardware tests with a custom quadrotor verify that STITCHER can produce trackable paths in real-time while respecting nonconvex constraints, such as limits on tilt angle and motor forces, which are otherwise hard to include in optimization-based planners.

• The paper presents an optimization-free, graph-based framework that stitches motion primitives to achieve constrained, real-time trajectory planning.
• It integrates sparse geometric path generation, velocity graph dynamic programming, and full-state motion primitive search to ensure collision-free, feasible trajectories.
• Experimental results demonstrate up to 400x planning speed improvement and zero constraint violations compared to state-of-the-art methods, validated in both simulation and hardware tests.

STITCHER: Constrained Trajectory Planning in Complex Environments with Real-Time Motion Primitive Search

Introduction and Motivation

The STITCHER framework addresses the challenge of real-time, long-range trajectory planning for autonomous aerial vehicles in complex environments, where dynamic feasibility, collision avoidance, and adherence to nonconvex state and actuator constraints are critical. Traditional optimization-based planners, while expressive, suffer from unpredictable computation times and numerical instability, especially in safety-critical scenarios. STITCHER circumvents these limitations by employing an optimization-free, graph-based approach that stitches together motion primitives—closed-form solutions to optimal control problems—using a multi-stage planning architecture with provable time and memory complexity bounds.

Figure 1: A trajectory generated by STITCHER in a Perlin noise environment, demonstrating real-time safe trajectory generation with complexity guarantees.

System Architecture and Algorithmic Innovations

STITCHER's architecture comprises three sequential planning stages:

1. Sparse Geometric Path Generation: An A* search over a voxelized map yields a collision-free waypoint sequence, which is sparsified to minimize the number of waypoints while maintaining connectivity.
2. Velocity Graph Construction and Dynamic Programming: At each waypoint, a set of velocity samples is generated. A velocity graph is constructed where nodes represent position-velocity pairs and edges correspond to minimum-time double integrator motion primitives. Dynamic programming (Bellman recursion) computes the cost-to-go for each node, forming an admissible heuristic for subsequent search.
3. Full-State Motion Primitive Search: An A* search is performed over a graph whose nodes encode full state (position, velocity, acceleration, etc.) and edges are higher-order motion primitives (e.g., triple integrator, LQMT). The heuristic from Stage 2 guides the search, and a greedy pre-processing step ensures the graph remains compact, avoiding exponential growth in edge count.

   Figure 2: System architecture illustrating the three planning stages: geometric path search, velocity graph dynamic programming, and motion primitive search.

Constraint Handling and Collision Checking

STITCHER enforces complex, nonconvex constraints—including thrust magnitude, tilt angle, and individual motor limits—by sampling candidate trajectories in time and pruning those that violate constraints. This approach is more general and less conservative than convex relaxation methods typical in optimization-based planners. Collision checking leverages a sphere-based safe set, reusing nearest-neighbor queries to avoid redundant computations and enabling efficient, on-the-fly addition of collision-free regions.

Figure 3: Achievable mass-normalized thrust for a VTOL vehicle under nonconvex thrust and tilt constraints.

Figure 4: Efficient collision checking by reusing safe spheres derived from previous nearest-neighbor queries.

Graph Construction and Complexity Analysis

The velocity and motion primitive graphs are proven to be finite, with node and edge counts determined solely by the number of waypoints and velocity samples. For $N$ waypoints and $M$ velocity samples, the velocity graph contains $(N-2)M + 2$ nodes and $(N-3)M^2 + 2M$ edges. The greedy pre-processing step in motion primitive graph construction maintains near-optimal connectivity while avoiding exponential edge growth, resulting in negligible loss in solution quality but substantial computational savings.

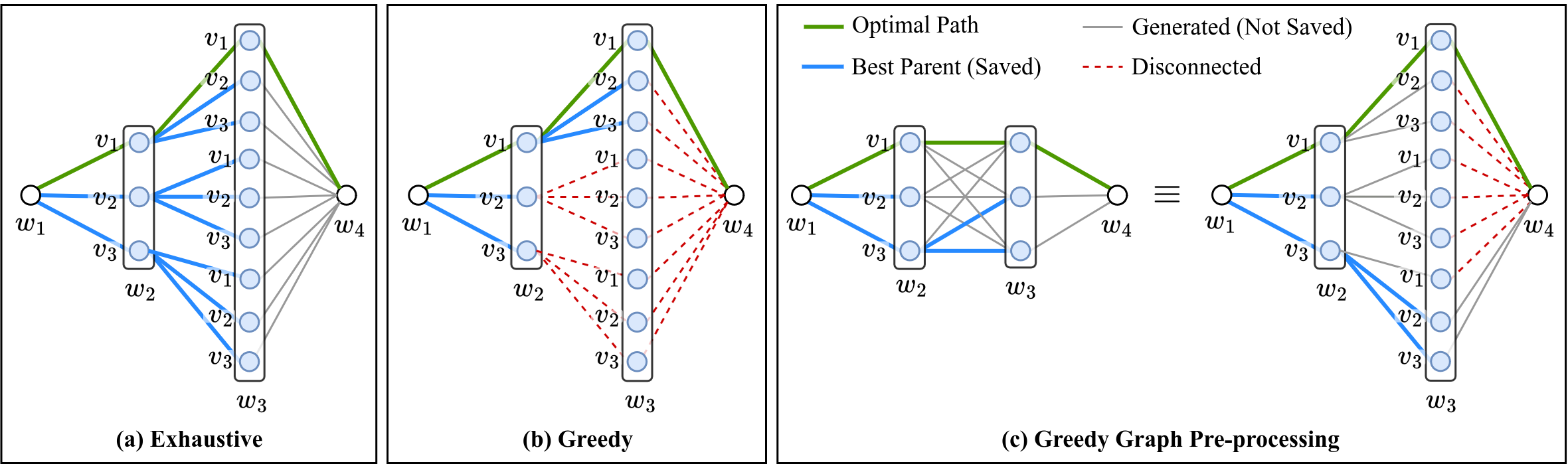
Figure 5: Comparison of exhaustive, greedy, and greedy pre-processed motion primitive graphs, highlighting the trade-off between connectivity and computational complexity.

Heuristic Admissibility and Optimality Guarantees

The cost-to-go computed via dynamic programming in the velocity graph is shown to be an admissible heuristic for the motion primitive search, regardless of the order of the integrator or the presence of nonconvex constraints. This guarantees resolution optimality of the resulting trajectory with respect to the discretized state space and ensures bounded time and memory complexity for the planner.

Simulation Studies

Extensive simulation experiments were conducted in two environments: Perlin Noise and Willow Garage, each spanning $50 \times 50$ meters. Key findings include:

• Velocity Sampling Trade-offs: Sparse velocity sampling ($|\mathcal{V}_m| = 5$) yields execution times within 8% of dense sampling, but with four orders of magnitude reduction in planning time.

  Figure 6: Speed discretization analysis showing convergence to Dense Dijkstra solution as sample count increases.

• Greedy Pre-processing Impact: The greedy graph pre-processing step results in less than 1% increase in solution cost, with up to 82% reduction in computation time for longer paths.

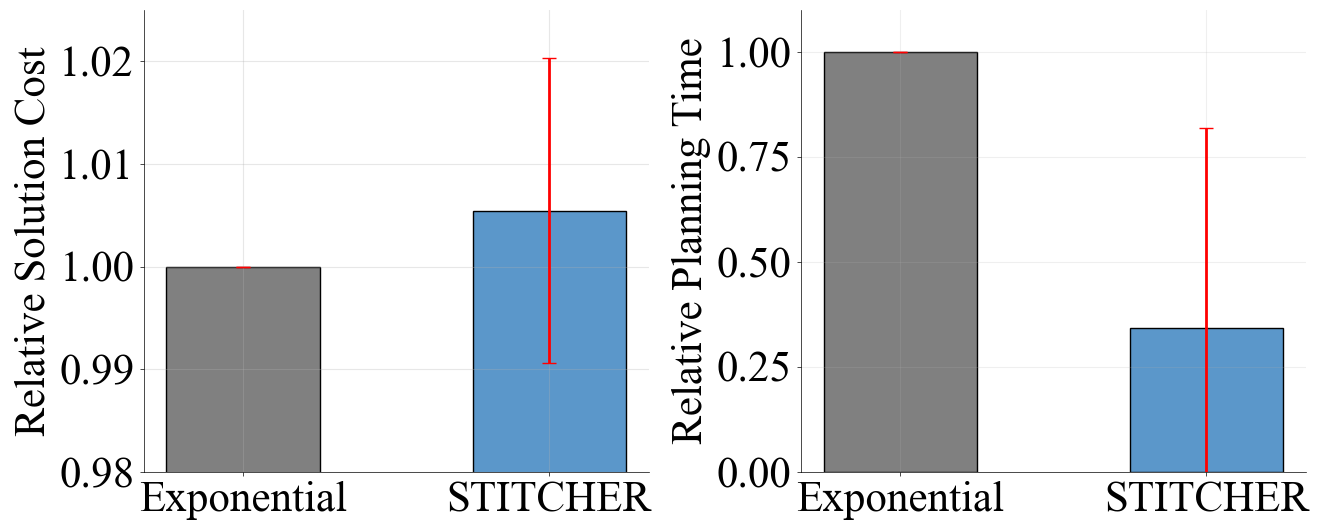
  Figure 7: Monte Carlo analysis of greedy pre-processing impact on solution cost and computation speed.

• Heuristic Effectiveness: The admissible heuristic reduces the number of generated edges by up to 30% compared to Dijkstra's algorithm, with further improvements possible using tighter acceleration constraints.

  Figure 8: Visualization of admissible and inadmissible acceleration constraints for heuristic evaluation.

• Constraint Satisfaction: STITCHER successfully plans trajectories that strictly satisfy individual motor thrust limits, demonstrating its flexibility in handling hardware-specific constraints.

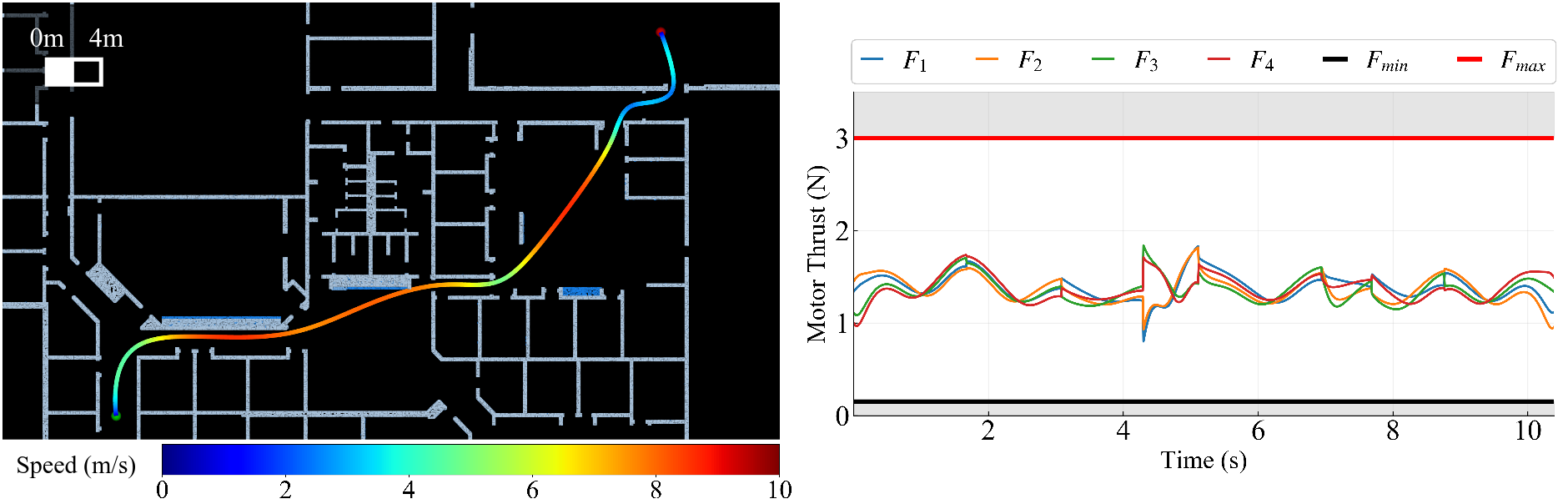
Figure 9: Case study of individual motor constraint satisfaction in trajectory planning.

Comparison with State-of-the-Art Planners

STITCHER was benchmarked against GCOPTER and FASTER, two leading optimization-based planners. Across all tested scenarios, STITCHER achieved:

• Faster Planning Times: Up to 400x speed-up over FASTER and 7x over GCOPTER.
• Zero Constraint Violations: STITCHER never violated state, actuator, or collision constraints, while optimization-based planners exhibited failures due to numerical instability or infeasible corridor generation.
• Comparable Execution Times: Minor differences in execution time were attributed to waypoint flexibility in optimization-based planners.

Hardware Validation

Indoor flight experiments with a custom quadrotor platform validated the dynamic feasibility and trackability of STITCHER-generated trajectories. The cascaded geometric controller tracked planned trajectories with position RMSE below 13.3 cm and tilt RMSE below 6.41 degrees across four distinct environments.

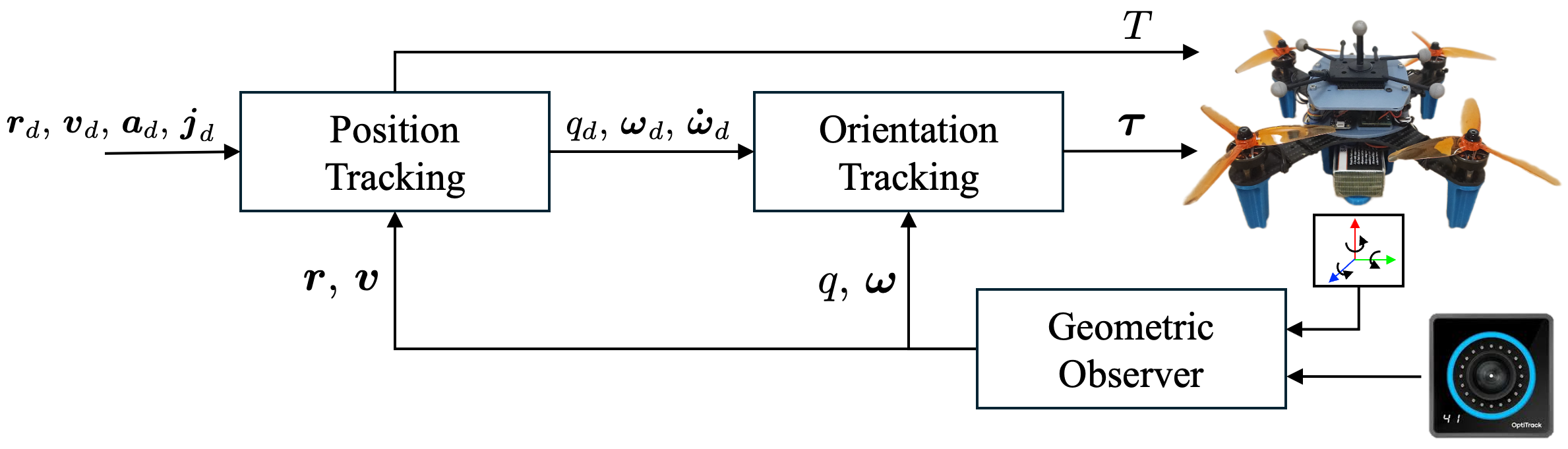
Figure 10: Control and estimation architecture for the quadrotor hardware platform.

Figure 11: Motion trail of quadrotor executing a STITCHER-planned trajectory in a drone cage.

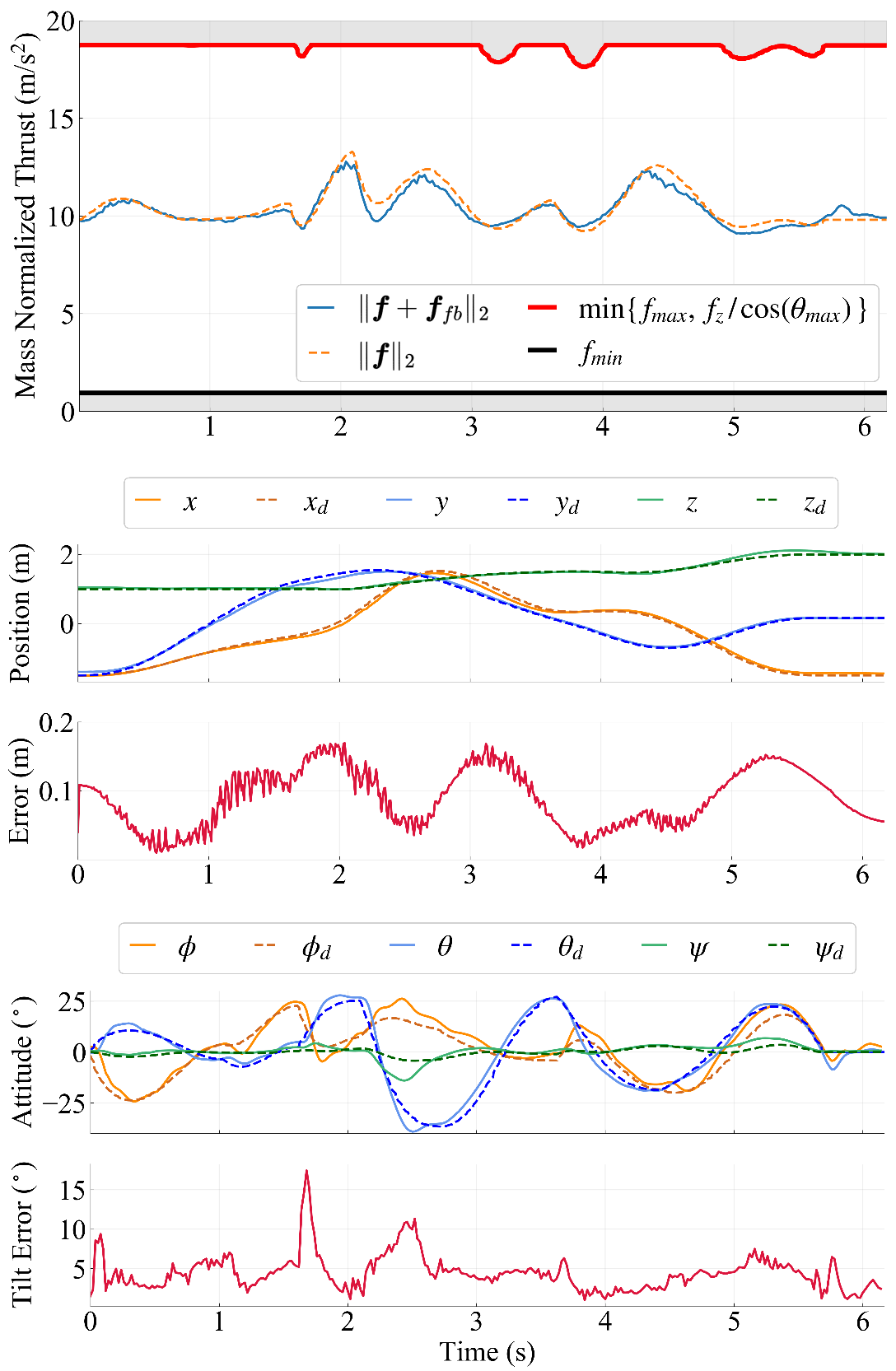
Figure 12: Comparison of actual and planned state profiles, demonstrating constraint satisfaction and low tracking error.

Implications and Future Directions

STITCHER's architecture provides strong theoretical guarantees on optimality and computational complexity, making it suitable for deployment in resource-constrained, safety-critical autonomous systems. Its ability to handle nonconvex constraints and hardware-specific actuator limits without resorting to conservative relaxations or offline computation is a significant practical advantage. The framework's modularity allows for extension to higher-order dynamics, more expressive motion primitives, and integration with learning-based heuristics or receding horizon strategies for operation in unknown environments.

Potential future developments include:

• Online Receding Horizon Planning: Enabling navigation in partially known or dynamic environments.
• Learning-Based Heuristics: Employing imitation or reinforcement learning to further reduce search effort.
• Generalization to Nonlinear Systems: Extending motion primitive libraries to cover broader classes of dynamics.

Conclusion

STITCHER presents a robust, real-time trajectory planning framework for complex environments, combining graph-based motion primitive search with admissible heuristics and efficient constraint/collision checking. Theoretical analysis, simulation, and hardware validation collectively demonstrate its effectiveness, scalability, and practical utility for autonomous aerial systems. The framework's design principles and empirical results suggest promising avenues for future research in constrained trajectory planning and autonomous navigation.