Heterogeneous RBCs via deep multi-agent reinforcement learning (2510.12272v1)

Abstract: Current macroeconomic models with agent heterogeneity can be broadly divided into two main groups. Heterogeneous-agent general equilibrium (GE) models, such as those based on Heterogeneous Agents New Keynesian (HANK) or Krusell-Smith (KS) approaches, rely on GE and 'rational expectations', somewhat unrealistic assumptions that make the models very computationally cumbersome, which in turn limits the amount of heterogeneity that can be modelled. In contrast, agent-based models (ABMs) can flexibly encompass a large number of arbitrarily heterogeneous agents, but typically require the specification of explicit behavioural rules, which can lead to a lengthy trial-and-error model-development process. To address these limitations, we introduce MARL-BC, a framework that integrates deep multi-agent reinforcement learning (MARL) with Real Business Cycle (RBC) models. We demonstrate that MARL-BC can: (1) recover textbook RBC results when using a single agent; (2) recover the results of the mean-field KS model using a large number of identical agents; and (3) effectively simulate rich heterogeneity among agents, a hard task for traditional GE approaches. Our framework can be thought of as an ABM if used with a variety of heterogeneous interacting agents, and can reproduce GE results in limit cases. As such, it is a step towards a synthesis of these often opposed modelling paradigms.

• The paper introduces MARL-BC, a framework that leverages deep multi-agent reinforcement learning to endogenously generate heterogeneous agent behavior and recover canonical RBC and KS models.
• It employs state-of-the-art RL algorithms like SAC, DDPG, TD3, and PPO with parameter sharing to enhance training efficiency and scalability across diverse agent populations.
• The framework accurately reproduces traditional macroeconomic dynamics, including impulse response functions, wealth distributions, and consumption policies, showcasing its practical implications for policy analysis.

Deep Multi-Agent Reinforcement Learning for Heterogeneous Real Business Cycles

Introduction

The paper "Heterogeneous RBCs via deep multi-agent reinforcement learning" (2510.12272) introduces the MARL-BC framework, which integrates deep multi-agent reinforcement learning (MARL) with Real Business Cycle (RBC) models to address the limitations of traditional macroeconomic approaches in modeling agent heterogeneity. Standard heterogeneous-agent general equilibrium (GE) models, such as HANK and Krusell-Smith (KS), are constrained by computational complexity and the rational expectations assumption, limiting the degree of heterogeneity that can be feasibly modeled. Agent-based models (ABMs), while flexible, require explicit behavioral rule specification, often leading to arbitrary or unrealistic agent behaviors. MARL-BC synthesizes these paradigms by enabling agents to learn optimal policies through interaction, thus endogenously generating heterogeneous behaviors without explicit rule design.

(Figure 1)

Figure 1: Schematic of the MARL-BC framework, showing $n$ RL household agents with heterogeneous productivities, aggregating capital and labor into production, and recovering RBC and KS models as limit cases.

MARL-BC Framework: Model Specification

The MARL-BC environment consists of $n$ household agents and a single firm. Each agent $i$ possesses individual capital $k^i_t$, labor $\ell^i_t$, and fixed productivities $\kappa^i$ (capital) and $\lambda^i$ (labor). Aggregate capital and labor are computed as weighted averages:

$$K_t = \frac{1}{n}\sum_{i=1}^{n} \kappa^i k^i_t, \qquad L_t = \frac{1}{n}\sum_{i=1}^{n} \lambda^i \ell^i_t$$

Production is determined by a Cobb-Douglas function:

$Y_t = A_t K_t^\alpha L_t^{1-\alpha}$

Wages and interest rates are proportional to marginal productivities:

$$r^i_t = \alpha \frac{Y_t}{K_t} \kappa^i, \qquad w^i_t = (1-\alpha) \frac{Y_t}{L_t} \lambda^i$$

Wealth dynamics for each agent are:

$$a^i_t = w^i_t \ell^i_t + r^i_t k^i_t + (1-\delta) k^i_t$$

Agents select actions $(\hat{c}^i_t, \ell^i_t)$, representing the fraction of wealth consumed and labor supplied. The reward function is:

$R^i_t = \log c^i_t + b \log(1 - \ell^i_t)$

where $b$ modulates the consumption-leisure trade-off. The observation space $\mathbf{x}^i_t$ includes individual and aggregate states, allowing for flexible agent information sets.

RL Algorithms and Training Paradigm

MARL-BC leverages state-of-the-art RL algorithms: SAC, DDPG, TD3, and PPO. Parameter sharing is employed, where a single neural network encodes policies for all agents, with agent-specific features (e.g., $\kappa^i$, $\lambda^i$) as inputs. This approach enhances sample efficiency and scalability, and supports emergent heterogeneous behaviors.

Figure 2: Mean rewards for different RL algorithms as a function of training steps, demonstrating sample efficiency and convergence properties.

Recovery of Canonical Macroeconomic Models

Representative-Agent RBC Limit

With $n=1$ and unit productivities, MARL-BC recovers the standard RBC model. For full capital depreciation ($\delta=1$), the optimal policy is analytically tractable:

$$\hat{c}^\star_t = 1 - \alpha\beta, \qquad \ell^\star_t = \frac{\alpha}{b(1-(1-\alpha)\beta) + \alpha}$$

MARL-BC agents trained with DDPG and SAC converge to these optimal choices within $10^4$ steps. For partial depreciation ($\delta=0.025$), MARL-BC matches solutions obtained via standard numerical solvers (e.g., Dynare), both in stationary choices and impulse response functions.

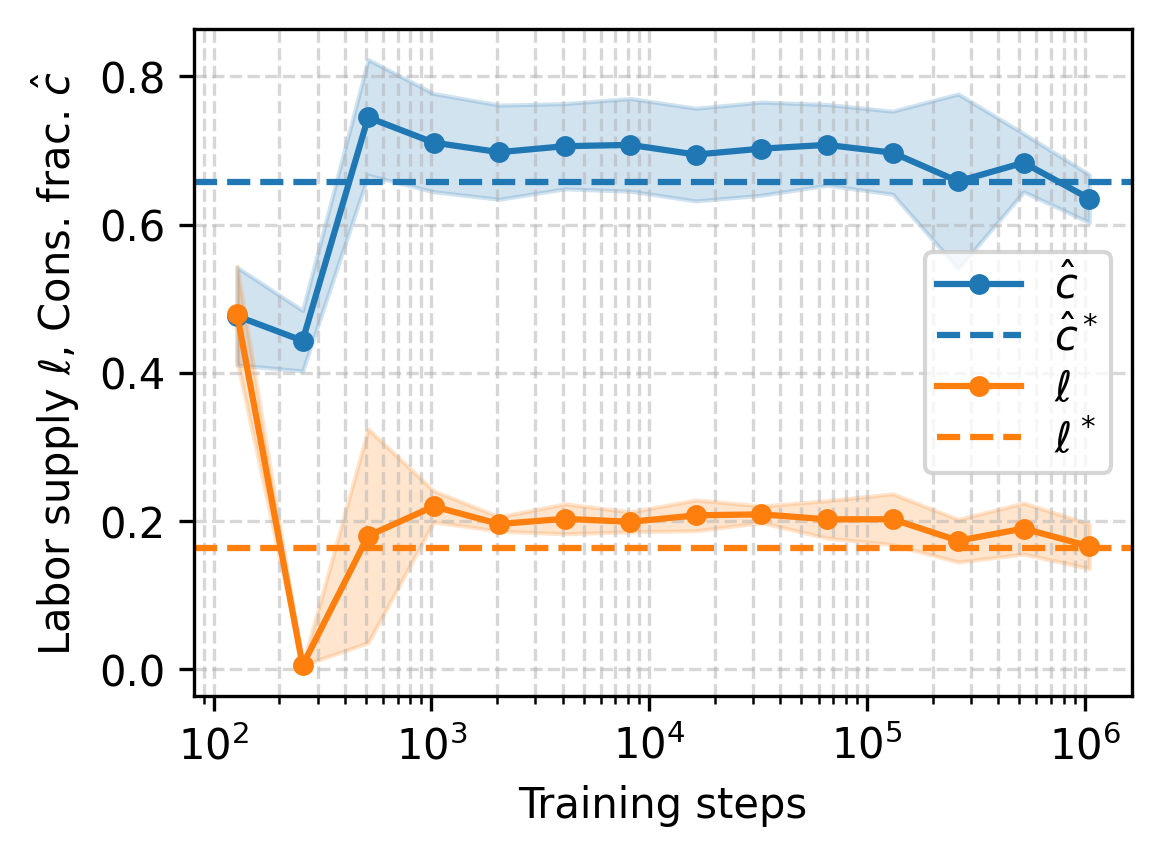
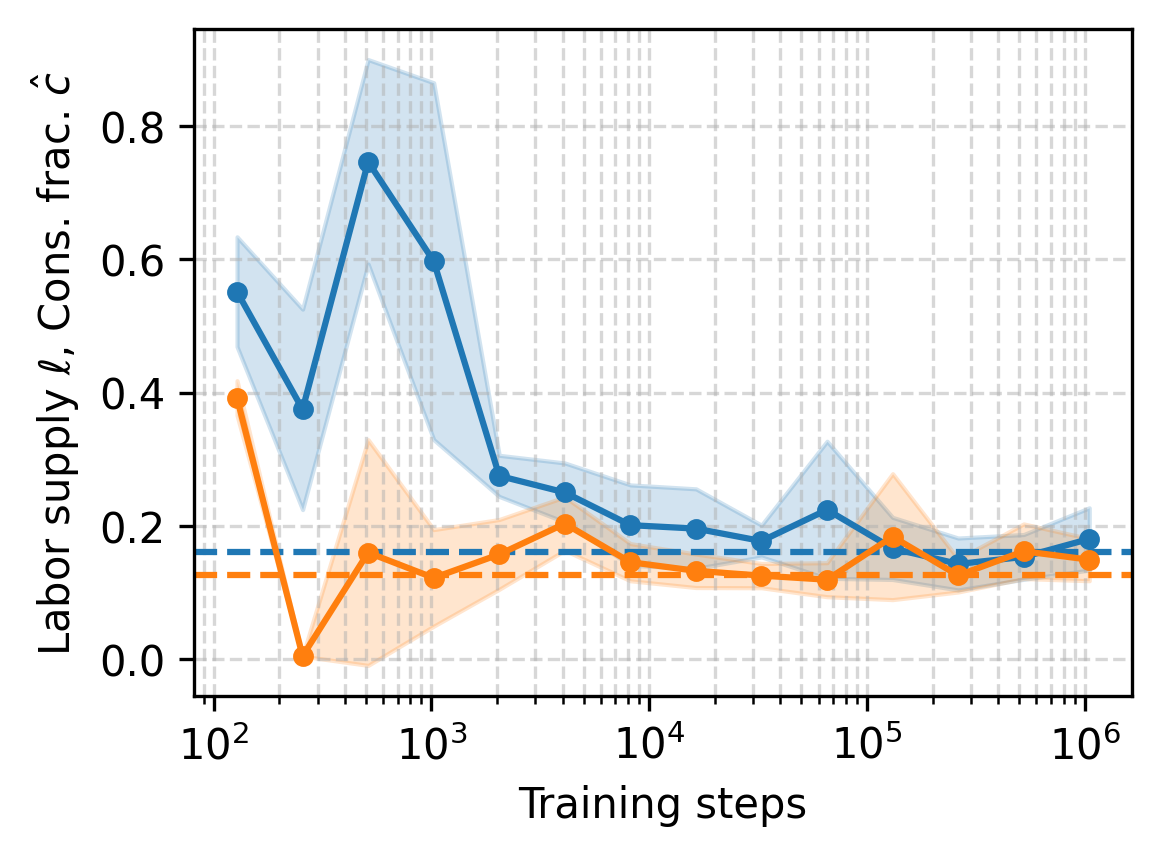
Figure 3: Convergence of RL agent policies to textbook RBC solutions for consumption and labor, and reproduction of impulse response functions.

Mean-Field Krusell-Smith Limit

With $n \gg 1$ and identical productivities, MARL-BC recovers KS model dynamics. Aggregate capital follows a linear law of motion, and wealth distributions and marginal propensities to consume match those in the original KS model. The Gini index and consumption policies learned by agents are consistent with established KS results.

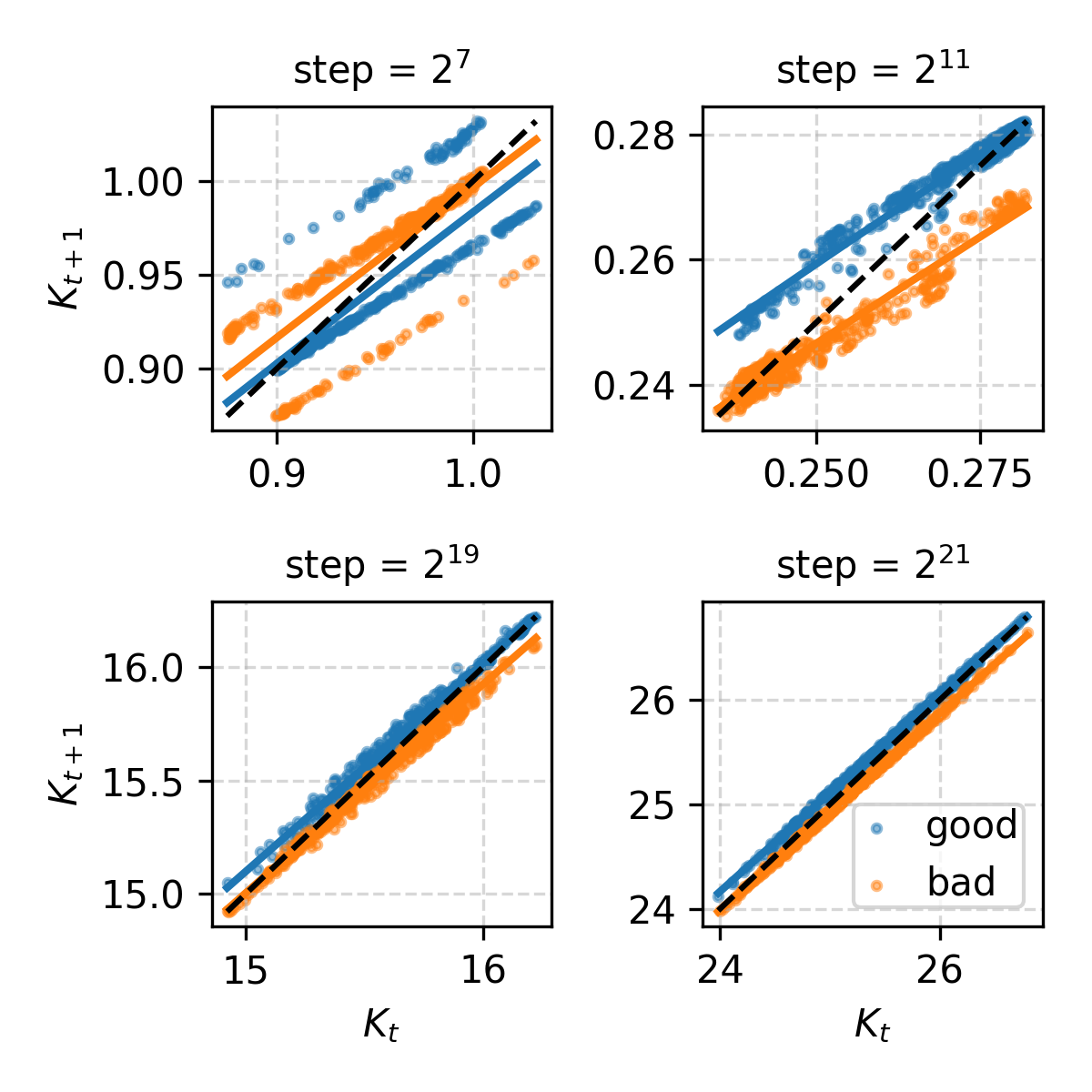
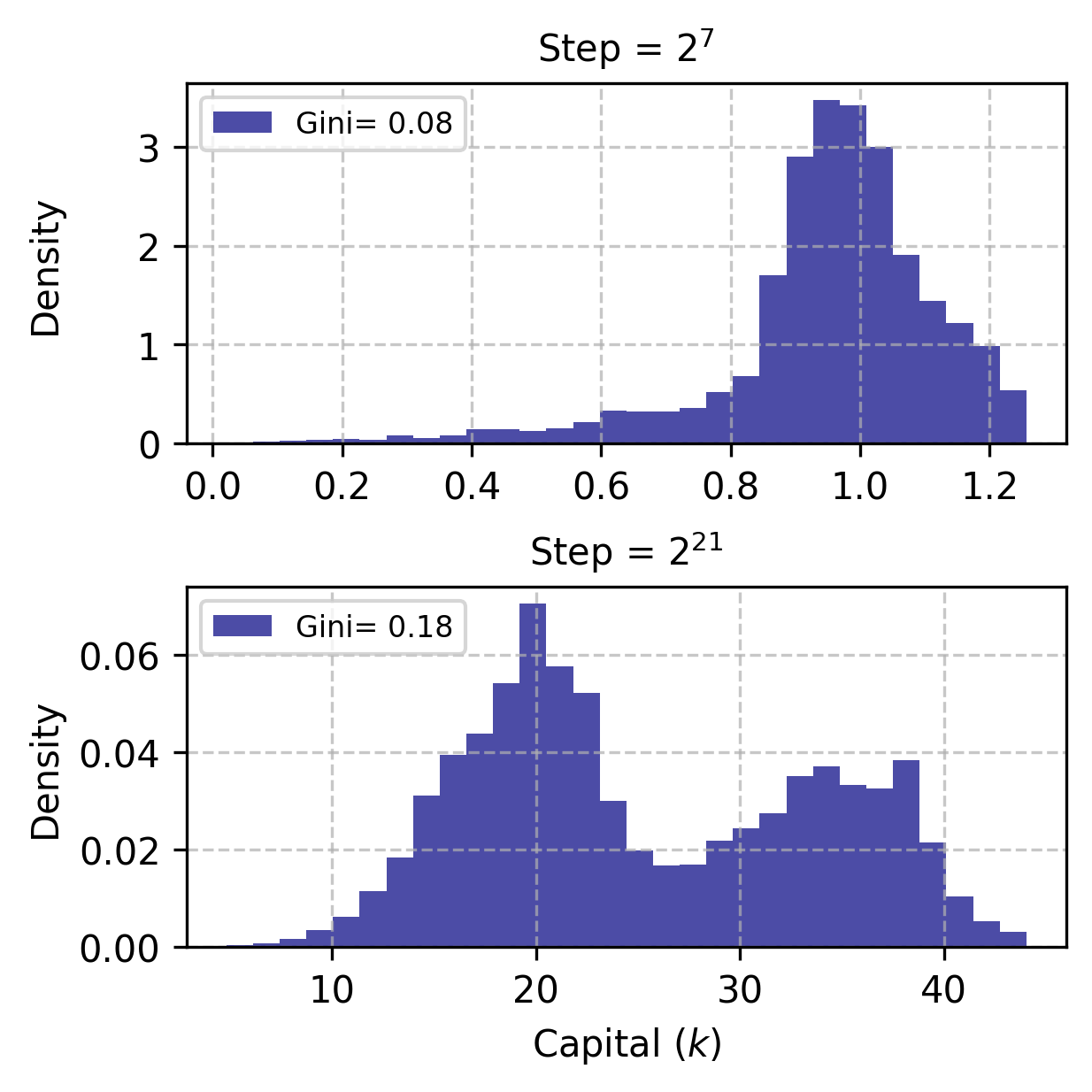
Figure 4: Emergence of KS law of motion for aggregate capital, wealth distributions, and marginal propensity to consume curves.

Modeling Rich Heterogeneity

MARL-BC enables ex-ante heterogeneity in capital and labor productivities, allowing for the simulation of economies with diverse agent types. Experiments with heterogeneous capital returns show that agents with low returns adopt "hand-to-mouth" consumption policies, while those with high returns accumulate wealth. The framework can model a wide range of wealth inequalities, as evidenced by Lorenz curves and Gini indices.

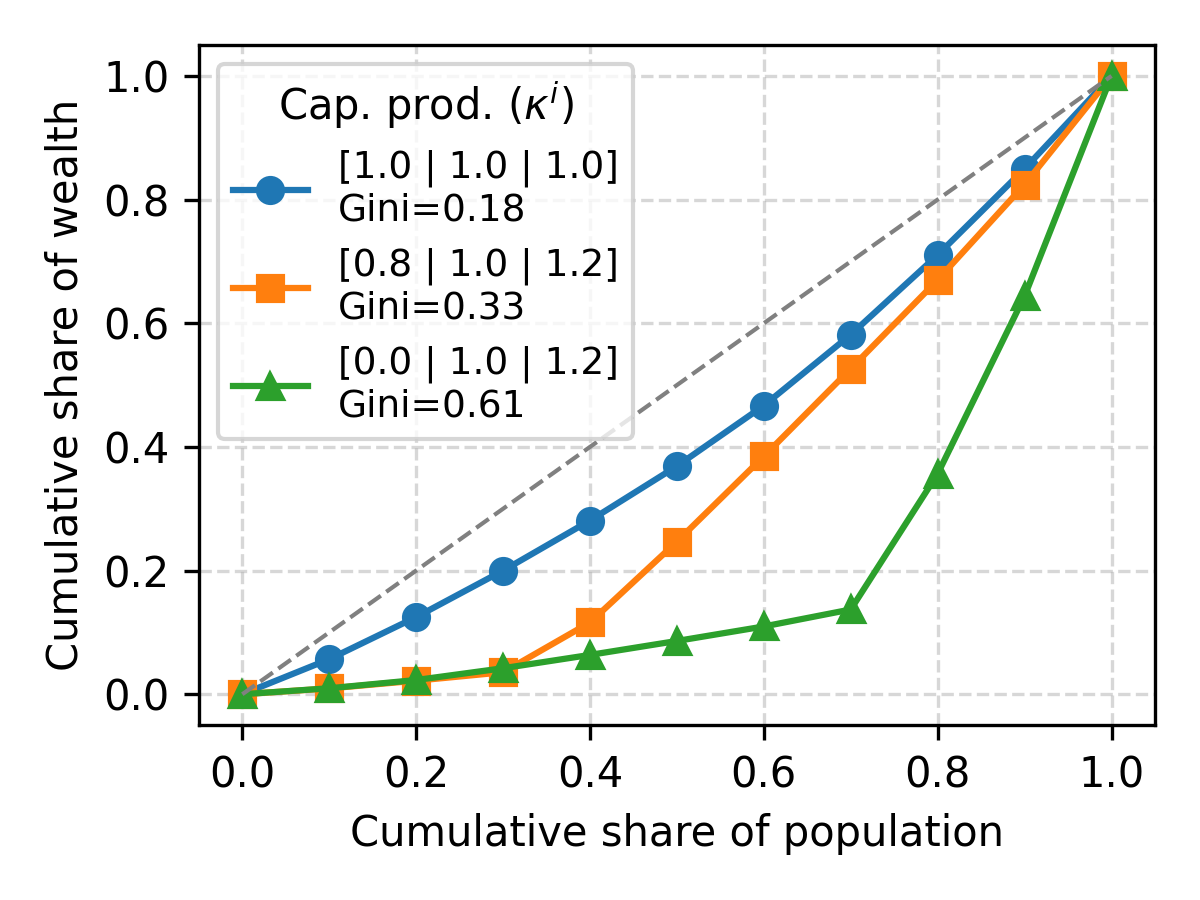
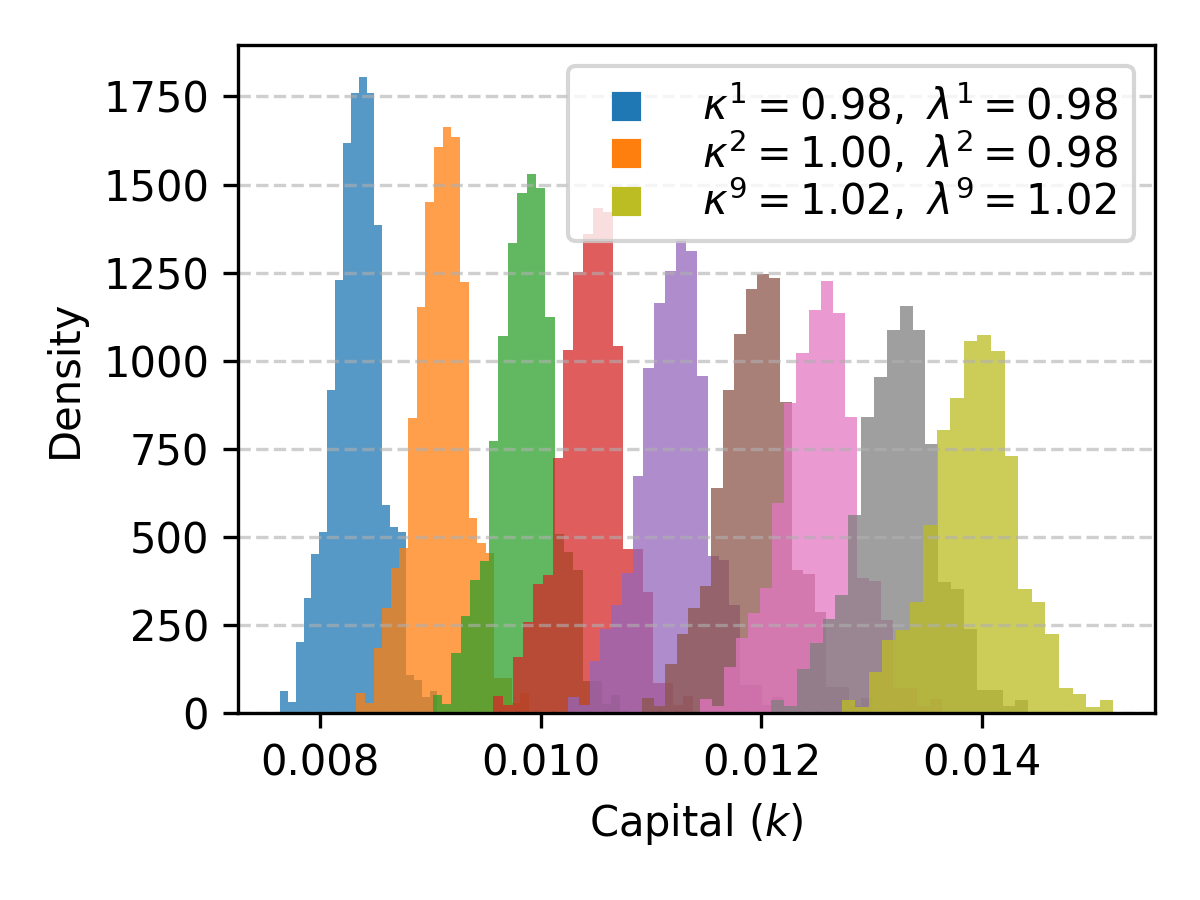
Figure 5: Lorenz curves and Gini indices for wealth distributions under varying degrees of agent heterogeneity, and emergent consumption policies.

Scalability and Computational Considerations

MARL-BC demonstrates scalability to hundreds of agents, with SAC maintaining stable performance and sample efficiency across population sizes. Training times remain practical on single-CPU hardware, and further acceleration is anticipated with vectorized GPU implementations.

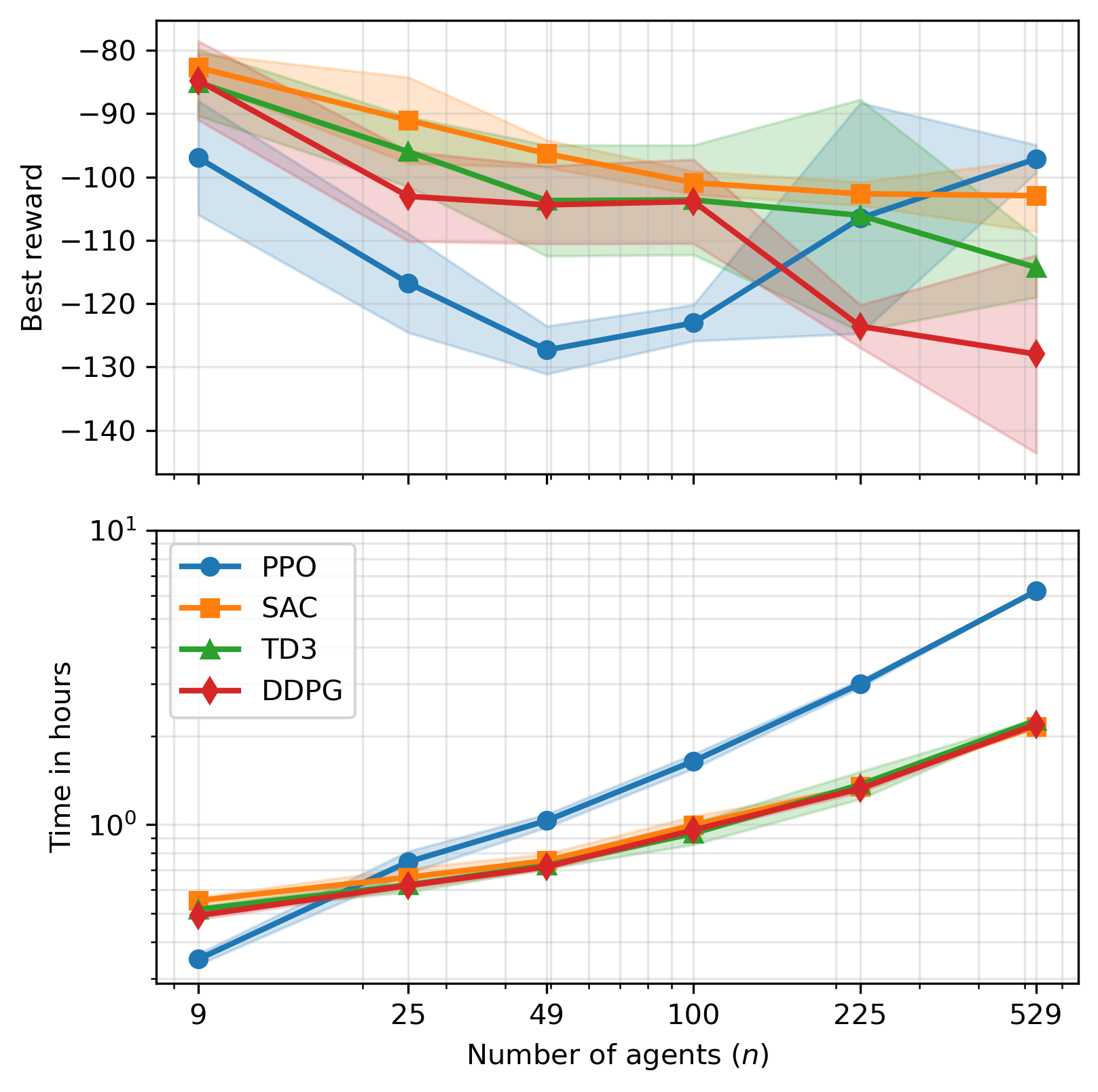
Figure 6: Best rewards and training times for MARL-BC as a function of agent population size, highlighting scalability and algorithmic trade-offs.

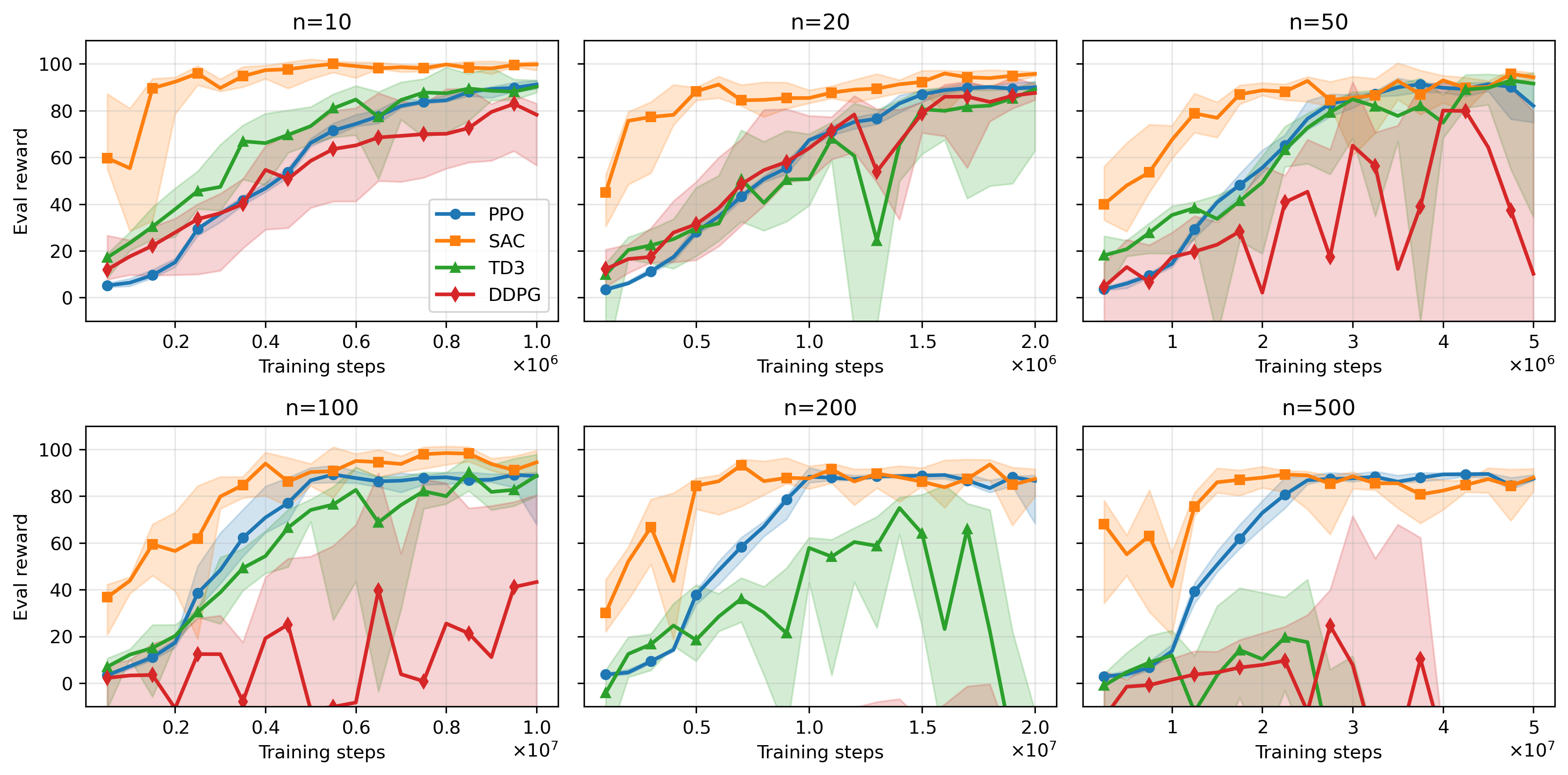
Figure 7: Learning curves for mean-field KS experiments across agent population sizes and RL algorithms.

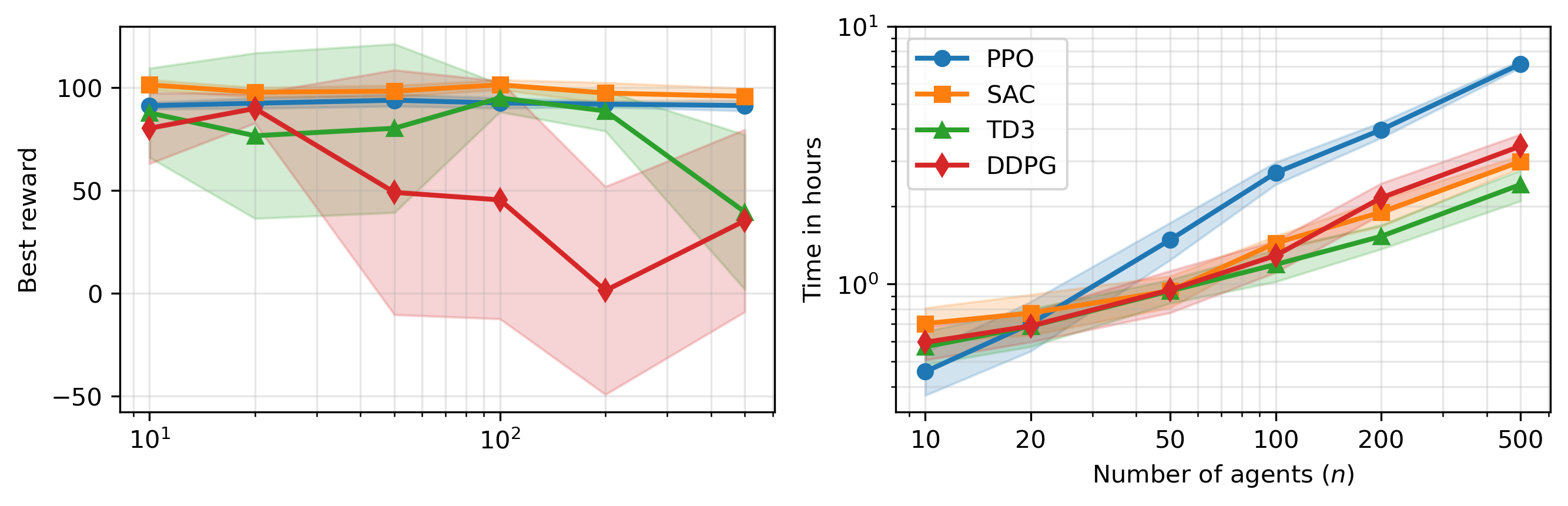
Figure 8: Scaling performance of MARL-BC in KS limit, showing reward stability and computational cost.

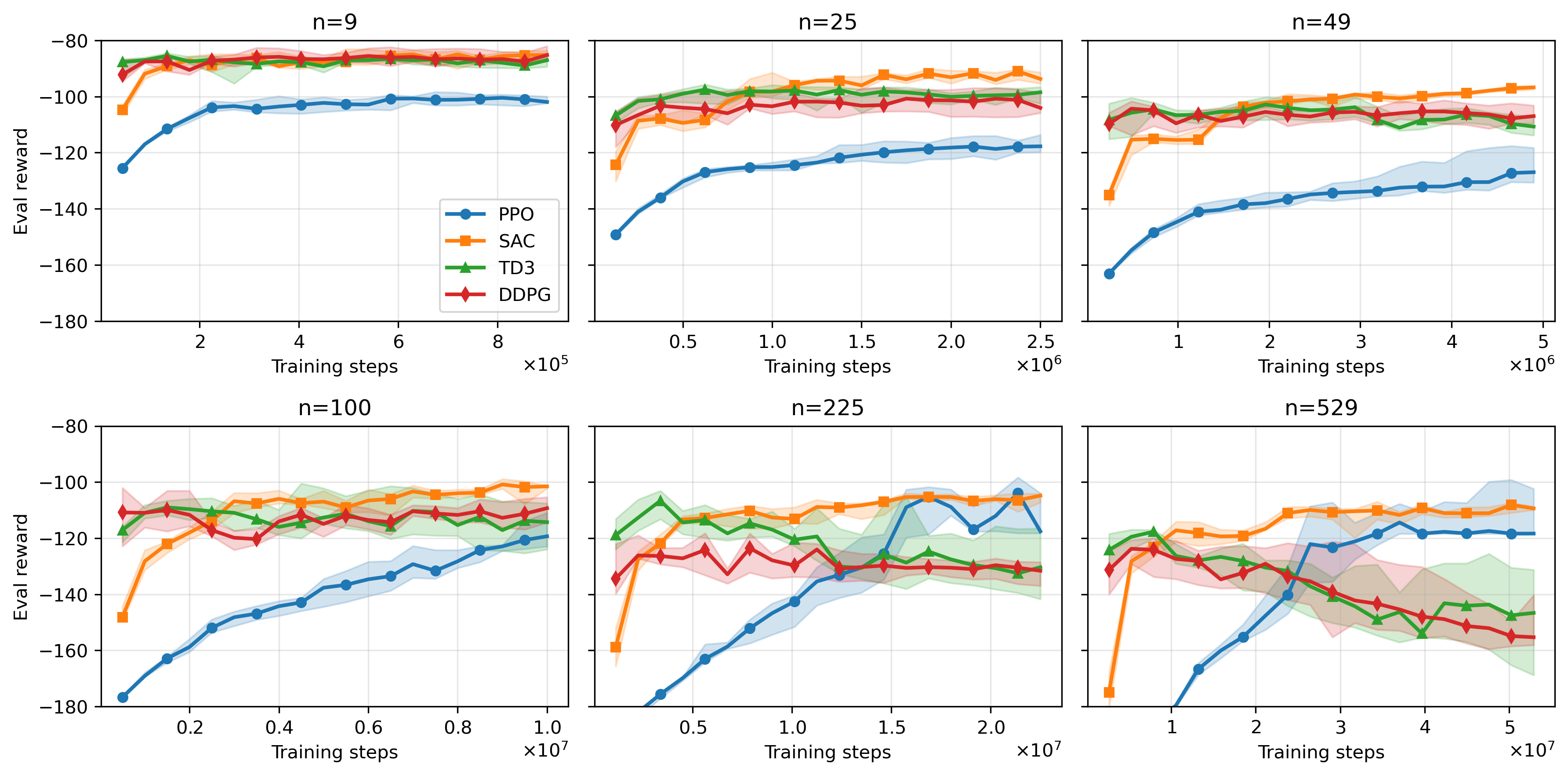
Figure 9: Learning curves for heterogeneous RBC experiments, demonstrating convergence and robustness across agent numbers.

Implications and Future Directions

MARL-BC bridges the gap between GE and ABM paradigms, providing a unified framework for modeling macroeconomic systems with rich agent heterogeneity and endogenous behavioral emergence. The approach circumvents the need for rational expectations and explicit behavioral rule specification, offering a scalable and principled alternative for macroeconomic simulation. The framework's flexibility enables the paper of distributional effects, policy interventions, and the impact of technological change (e.g., AI-driven shifts in labor productivity).

The main limitation is computational cost, particularly for large-scale multi-agent training. However, advances in vectorized RL environments and GPU acceleration are expected to mitigate this issue. Future work should explore MARL-BC applications to policy analysis, inequality dynamics, and integration with more complex macro-financial environments.

Conclusion

The MARL-BC framework provides a robust and scalable methodology for simulating heterogeneous macroeconomic systems using deep multi-agent reinforcement learning. It successfully recovers canonical RBC and KS results, extends them to richer heterogeneity, and demonstrates practical scalability. MARL-BC offers a promising direction for synthesizing GE and ABM approaches, with significant implications for both theoretical and applied macroeconomics.