Emergence of hybrid computational dynamics through reinforcement learning (2510.11162v1)

Abstract: Understanding how learning algorithms shape the computational strategies that emerge in neural networks remains a fundamental challenge in machine intelligence. While network architectures receive extensive attention, the role of the learning paradigm itself in determining emergent dynamics remains largely unexplored. Here we demonstrate that reinforcement learning (RL) and supervised learning (SL) drive recurrent neural networks (RNNs) toward fundamentally different computational solutions when trained on identical decision-making tasks. Through systematic dynamical systems analysis, we reveal that RL spontaneously discovers hybrid attractor architectures, combining stable fixed-point attractors for decision maintenance with quasi-periodic attractors for flexible evidence integration. This contrasts sharply with SL, which converges almost exclusively to simpler fixed-point-only solutions. We further show that RL sculpts functionally balanced neural populations through a powerful form of implicit regularization -- a structural signature that enhances robustness and is conspicuously absent in the more heterogeneous solutions found by SL-trained networks. The prevalence of these complex dynamics in RL is controllably modulated by weight initialization and correlates strongly with performance gains, particularly as task complexity increases. Our results establish the learning algorithm as a primary determinant of emergent computation, revealing how reward-based optimization autonomously discovers sophisticated dynamical mechanisms that are less accessible to direct gradient-based optimization. These findings provide both mechanistic insights into neural computation and actionable principles for designing adaptive AI systems.

• The paper demonstrates that reinforcement learning uniquely discovers hybrid attractor architectures that combine stable fixed-point and quasi-periodic dynamics.
• It employs dynamical systems analysis and information-theoretic metrics to quantify the emergence and stability of these network states.
• The study reveals that reward-driven exploration and weight initialization width are crucial factors in sculpting organized, balanced neural populations.

Emergence of Hybrid Computational Dynamics through Reinforcement Learning

Overview and Motivation

This work systematically investigates how the choice of learning paradigm—reinforcement learning (RL) versus supervised learning (SL)—fundamentally shapes the computational strategies that emerge in recurrent neural networks (RNNs) trained on context-dependent decision-making tasks. The central claim is that RL, via reward-driven exploration, autonomously discovers hybrid attractor architectures that combine stable fixed-point attractors for decision maintenance with quasi-periodic attractors for flexible evidence integration. In contrast, SL converges almost exclusively to fixed-point-only solutions. The paper employs dynamical systems analysis, information-theoretic metrics, and population-level characterization to elucidate the mechanisms underlying these divergent outcomes.

Experimental Framework and Task Structure

The primary experimental paradigm is a context-dependent decision-making (CtxDM) task, requiring the network to integrate one of two noisy stimulus streams based on a contextual cue, with distinct fixation, stimulus, delay, and decision stages. The RNN architecture is vanilla, with ReLU nonlinearities and a hidden layer size of $N_{hidden}=250$, ensuring sufficient capacity for complex dynamics while maintaining tractability. Networks are trained using PPO for RL and Adam with cross-entropy loss for SL, with systematic variation of weight initialization width $\delta$ to probe its effect on emergent dynamics.

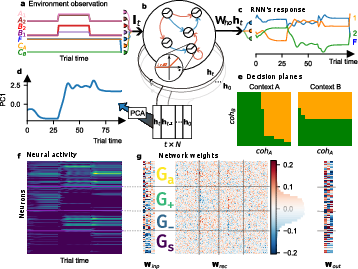
Figure 1: Task structure, RNN architecture, and emergent population-level connectivity in RL-trained networks.

Dynamical Landscape: RL vs. SL

A key result is the quantification of attractor types in the stationary regime during prolonged stimulus presentation. RL-trained networks exhibit a high prevalence of quasi-periodic (oscillatory) attractors, especially for ambiguous, low-coherence stimuli, whereas SL-trained networks overwhelmingly converge to stable fixed points. This divergence is robust across ensembles and is amplified by broader weight initializations in RL, which promote dynamical richness, while SL actively prunes such complexity.

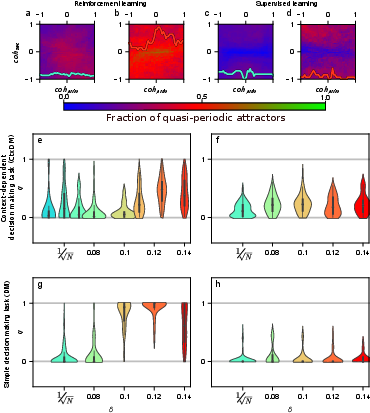
Figure 2: RL discovers quasi-periodic attractors for ambiguous stimuli, while SL converges to fixed points; prevalence is modulated by initialization width.

Linear stability analysis confirms the attractor classification, with quasi-periodic regimes corresponding to leading eigenvalues of the Jacobian matrix exceeding unity in modulus, and fixed points corresponding to subunitary eigenvalues.

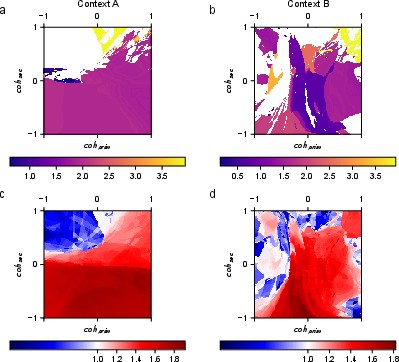
Figure 3: Distribution of oscillation frequencies and leading eigenvalues, validating attractor classification methodology.

Emergence of Hybrid Attractor Architectures

RL does not merely increase dynamical diversity; it organizes the network into a hybrid computational system. Low-dimensional projections of neural trajectories reveal a separation of computational functions: decisions are encoded by discrete, stable fixed-point attractors, while sensory evidence is integrated along a continuous manifold, often exhibiting quasi-periodic dynamics. This separation emerges progressively during training, with the reward signal guiding the elongation and bifurcation of the state space.

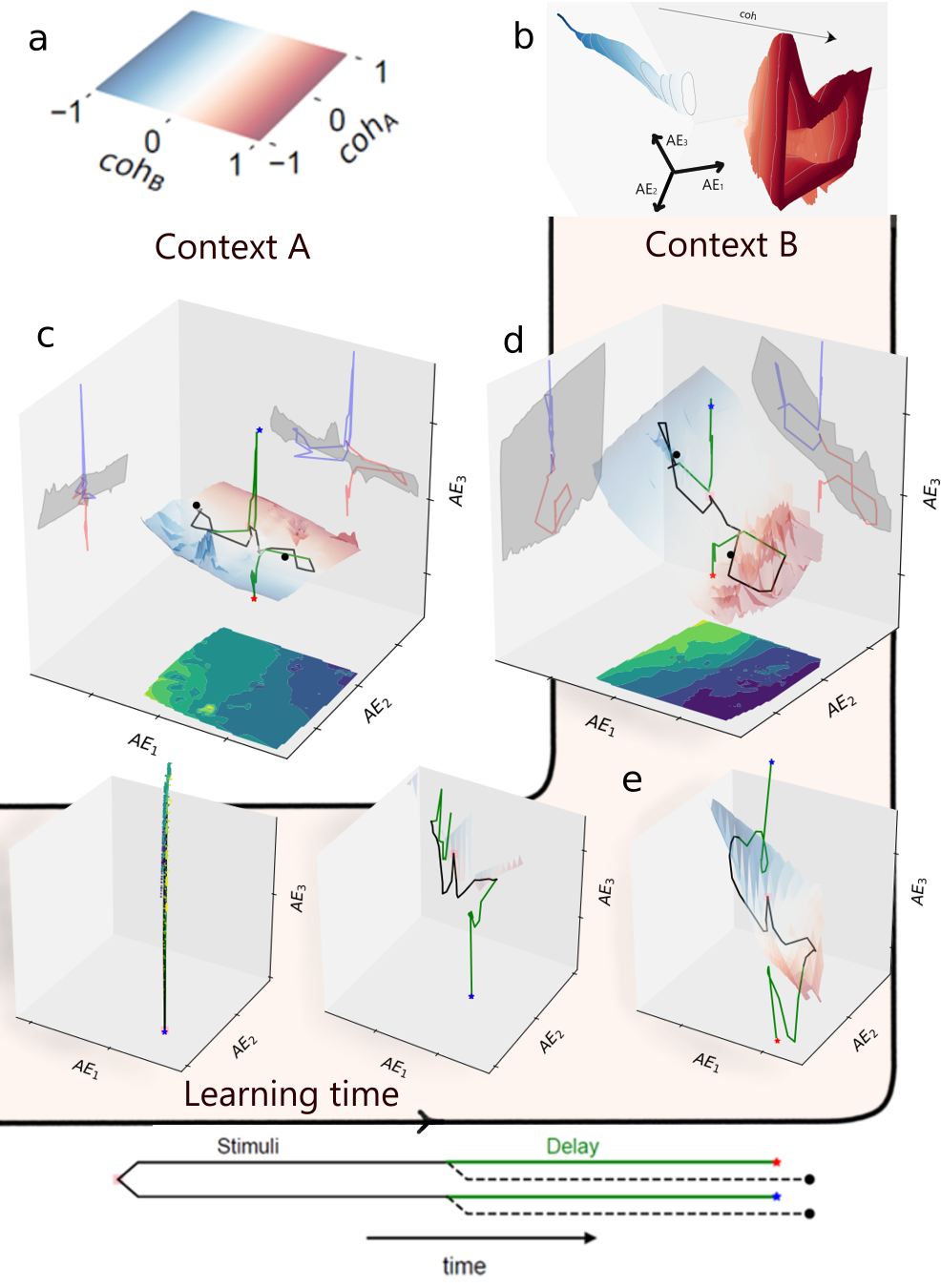
Figure 4: Progressive sculpting of state space during RL, culminating in a hybrid architecture with distinct encoding and decision subspaces.

Quasi-periodic attractors provide a dynamic mechanism for maintaining stimulus information, as opposed to static memory traces.

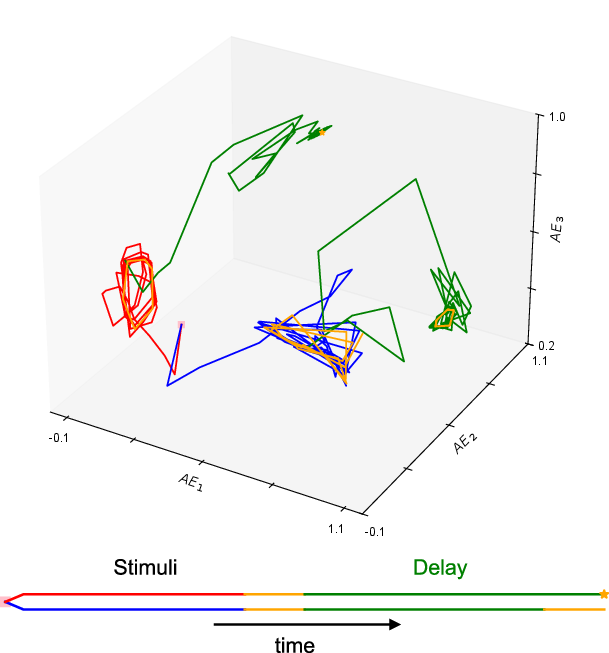
Figure 5: Example of quasi-periodic attractor dynamics during stimulus encoding.

Population-Level Self-Organization

RL induces the self-organization of the network into four functionally distinct neural populations: silent ($\mathrm{G}_s$), positive coherence-selective ($\mathrm{G}_+$), negative coherence-selective ($\mathrm{G}_-$), and context-integrating ($\mathrm{G}_a$). The emergence of balanced, opposing coherence-selective populations is tightly coupled to performance gains and the bifurcation of the decision landscape into bistable attractors. This population balance acts as an implicit regularizer, preventing over-specialization and enhancing robustness.

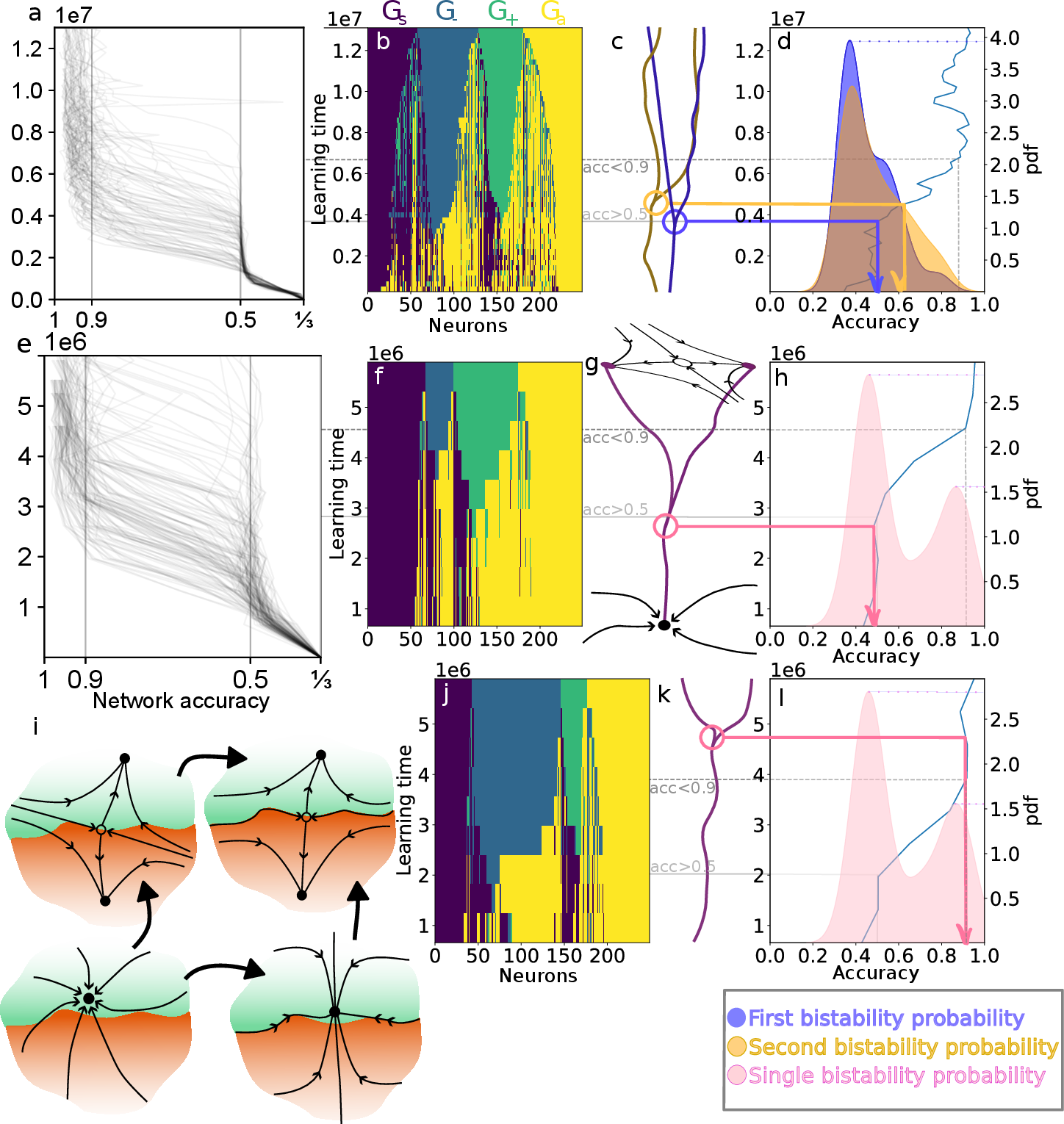
Figure 6: Coupling of population self-organization, performance gains, and bistability during RL.

Information-theoretic analysis (mutual information) confirms the functional specialization of these populations, with $\mathrm{G}_+$ and $\mathrm{G}_-$ encoding positive and negative coherence, respectively.

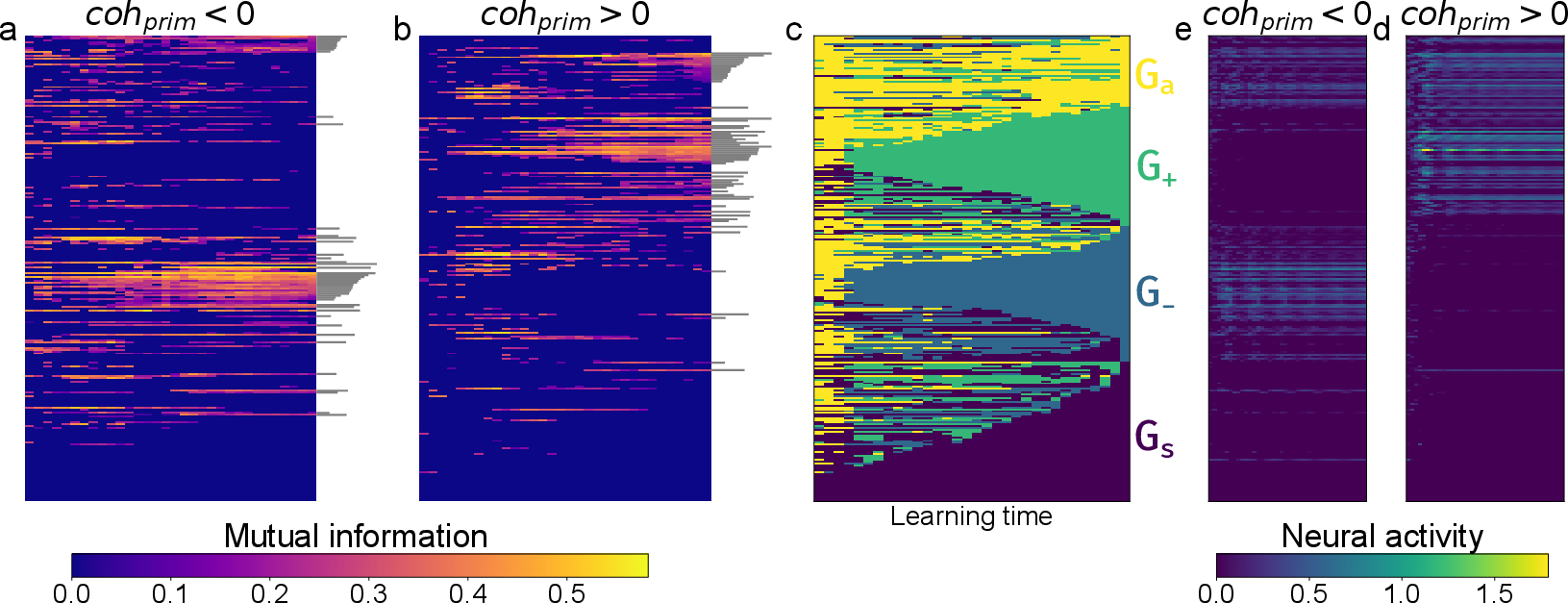
Figure 7: Distinct information encoding roles of dynamically-defined populations.

Population classification is performed via template-matching on activity-type matrices across the coherence space, providing an objective assignment of neurons to functional groups.

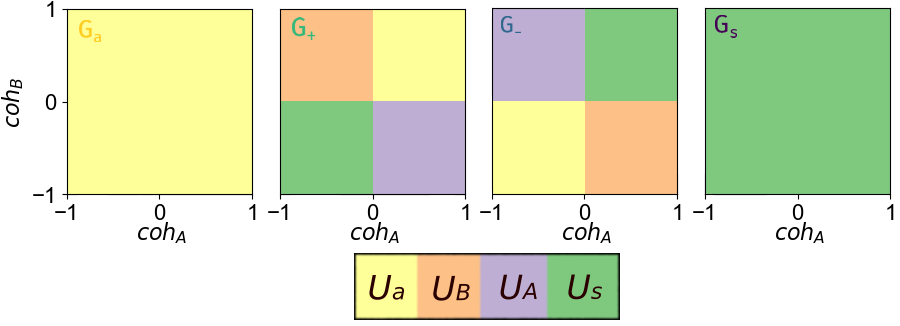
Figure 8: Idealized templates for neural population classification.

In contrast, SL-trained networks exhibit more heterogeneous and imbalanced population structures, lacking the regularization and balance found in RL solutions.

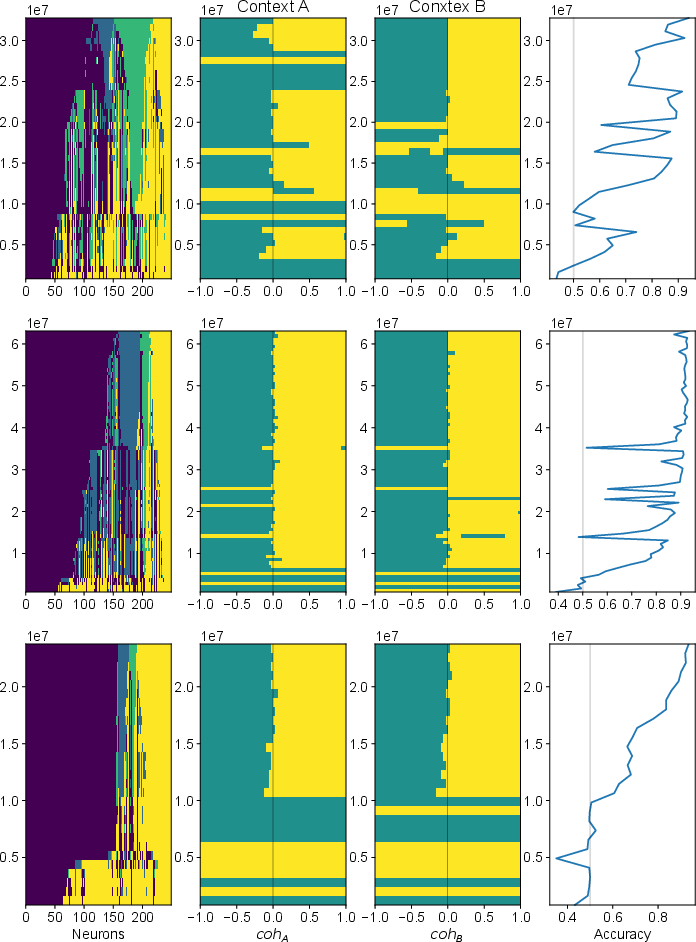
Figure 9: Heterogeneous population structure in SL-trained networks.

Modulation by Weight Initialization and Training Stability

The width of the initial weight distribution ($\delta$) modulates both the prevalence of quasi-periodic dynamics and the size of the silent population in RL networks. Broader initializations facilitate the construction of complex, oscillatory dynamics by providing a pool of uncommitted neurons.

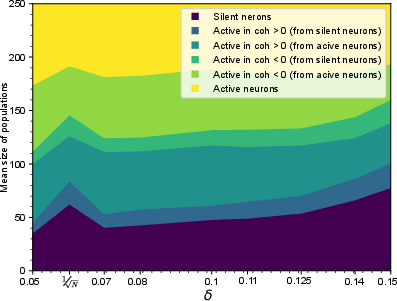
Figure 10: Effect of initialization width on population sizes in RL networks.

Training stability is sensitive to initialization width, with extremes leading to gradient explosion or vanishing and reduced probability of successful training.

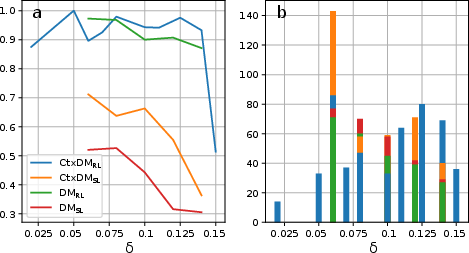
Figure 11: Training stability and ensemble sizes as a function of initialization width.

Theoretical and Practical Implications

The findings establish the learning algorithm as a primary determinant of emergent computation, with RL's reward-driven exploration discovering a richer class of dynamical solutions than SL's explicit error correction. The hybrid attractor architecture provides a computational model that reconciles persistent and dynamic coding mechanisms in working memory, paralleling functional motifs observed in biological circuits. The population-level regularization induced by RL suggests new strategies for designing robust AI systems, including hybrid training schemes that combine SL for rapid coarse learning and RL for fine-tuning dynamical richness.

The paper also highlights the importance of prolonged representational refinement ("crystallization" or "grokking") beyond immediate performance metrics, suggesting a general principle for learning in complex systems. The emergent push-pull connectivity and mixed selectivity mirror cortical microcircuit organization, supporting the view that many features of biological computation are convergent solutions discovered through goal-directed learning.

Limitations and Future Directions

The analysis is restricted to a single task paradigm and a vanilla RNN architecture. Extension to other cognitive domains, more biologically realistic models (e.g., spiking networks, Dale's law), and alternative learning algorithms is necessary to assess generalizability. Causal interventions to test the functional necessity of quasi-periodic dynamics are proposed as future work.

Conclusion

This paper reframes RL as a discovery engine for novel computational principles, demonstrating that reward-driven exploration autonomously produces hybrid attractor architectures and balanced population structures that enhance robustness and flexibility. The mechanistic insights provided here are foundational for both neuroscience and AI, offering actionable principles for the design of adaptive, multi-timescale cognitive systems.