Image reconstruction with the JWST Interferometer (2510.10924v1)
Abstract: Flying on board the James Webb Space Telescope (JWST) above Earth's turbulent atmosphere, the Aperture Masking Interferometer (AMI) on the NIRISS instrument is the highest-resolution infrared interferometer ever placed in space. However, its performance was found to be limited by non-linear detector systematics, particularly charge migration - or the Brighter-Fatter Effect. Conventional interferometric Fourier observables are degraded by non-linear transformations in the image plane, with the consequence that the inner working angle and contrast limits of AMI were seriously compromised. Building on the end-to-end differentiable model & calibration code amigo, we here present a regularised maximum-likelihood image reconstruction framework dorito which can deconvolve AMI images either in the image plane or from calibrated Fourier observables, achieving high angular resolution and contrast over a wider field of view than conventional interferometric limits. This modular code by default includes regularisation by maximum entropy, and total variation defined with $l_1$ or $l_2$ metrics. We present imaging results from dorito for three benchmark imaging datasets: the volcanoes of Jupiter's moon Io, the colliding-wind binary dust nebula WR 137 and the archetypal Seyfert 2 active galactic nucleus NGC 1068. In all three cases we recover images consistent with the literature at diffraction-limited resolutions. The performance, limitations, and future opportunities enabled by amigo for AMI imaging (and beyond) are discussed.
Summary
- The paper introduces a differentiable forward-modeling framework using regularized maximum likelihood to accurately reconstruct interferometric images from JWST data.
- The methodology mitigates non-linear detector effects like the Brighter-Fatter Effect and validates performance across diverse astrophysical targets.
- Empirical results on NGC 1068, Io, and WR 137 demonstrate effective image plane and DISCO-based fitting, ensuring diffraction-limited imaging even with calibration challenges.
Image Reconstruction with the JWST Interferometer: Methods, Results, and Implications
Introduction
The paper "Image reconstruction with the JWST Interferometer" (2510.10924) presents a comprehensive framework for high-fidelity image reconstruction from data acquired by the James Webb Space Telescope (JWST) Non-Redundant Mask (NRM) mode on the NIRISS instrument. The authors address the limitations imposed by detector systematics—most notably the Brighter-Fatter Effect (BFE)—on conventional interferometric analysis, and introduce a regularized maximum-likelihood (RML) approach implemented in the open-source dorito package. The methodology is validated on three astrophysically diverse targets: the AGN NGC 1068, Jupiter's moon Io, and the colliding-wind binary WR 137, demonstrating diffraction-limited imaging performance and robust recovery of complex scene morphologies.
Figure 1: Interferograms and RML reconstructions for NGC 1068, Io, and WR 137, illustrating the transition from raw data to deconvolved images at the JWST diffraction limit.
Instrumental Context and Motivation
JWST's NIRISS/AMI mode employs a 7-hole non-redundant mask, enabling sparse aperture masking interferometry in space. While this configuration offers self-calibrating closure phase observables, the performance is fundamentally limited by non-linear detector effects, particularly BFE-induced charge migration. The BFE introduces non-linearities that cannot be fully calibrated in the Fourier domain, degrading sensitivity and contrast, especially for faint companion searches and high-dynamic-range imaging. The authors argue for a forward-modeling approach that operates directly on the image plane, leveraging differentiable programming frameworks (JAX) to enable gradient-based optimization and Bayesian inference.
Forward Modeling and Regularized Maximum Likelihood
The core methodological advance is the adoption of an end-to-end differentiable forward model of the JWST instrument, encapsulating both optical and detector physics. This model is trained on calibration data to fix instrumental parameters, while astrophysical scene parameters are inferred via optimization or sampling. The RML framework is formalized as:
where is the log-likelihood of the data given the image, and is a regularization (log-prior) term. The image is parameterized in a pixel basis, with regularization imposed via maximum entropy, / norms, quadratic variation, or total variation (TV). The selection of the regularization strength is guided by L-curve analysis, balancing data fidelity and prior constraints.
Figure 2: L-curve for TV regularization on Io, with reconstructions illustrating the trade-off between data fit and regularization-induced smoothness.
Image Reconstruction Methods
Two primary reconstruction strategies are developed:
Method 1: Image Plane Fitting
This approach fits the forward model directly to the ramp data in the image plane, bypassing the extraction of complex visibilities. The source distribution is convolved with a small Gaussian kernel at each iteration to mitigate pixel-level sparsity, and positivity is enforced via log-space parameterization. This method is robust to detector non-linearities and is the default for most targets.
Figure 3: Schematic of Method 1, showing direct image plane fitting via convolutional forward modeling and gradient descent.
Method 2: DISCO-Based Fitting
Here, the forward model is used to extract complex visibilities, which are then transformed into the Delay-Insensitive Subspace of Calibrated Observables (DISCOs)—generalized kernel phases that are self-calibrating against wavefront errors. The image is reconstructed by fitting to these DISCOs, with additional priors to constrain the image centroid due to translation invariance. This method is particularly effective when wavefront miscalibration dominates, as in the presence of mirror tilt events.
Empirical Results
NGC 1068: AGN Torus and Outflow
The RML reconstruction of NGC 1068 recovers the extended structure of the AGN torus and outflow, with excellent agreement to mid-IR LBTI imaging. The multi-band JWST image shows consistent morphology across filters, and the spatial correspondence with LBTI contours confirms the fidelity of the reconstruction.
Figure 4: Comparison of JWST and LBTI images of NGC 1068, demonstrating consistent recovery of the AGN torus and outflow structure across independent instruments.
Io: Volcanic Surface Features
For Io, Method 1 with TV regularization yields high-resolution images that resolve the disk and track the rotation of the moon over multiple exposures. Five known volcanic features are detected at their expected positions, and the temporal evolution is consistent with Io's rotation. The method outperforms neural network-based deconvolution in terms of limb sharpness and spatial resolution.
Figure 5: Time series of Io reconstructions, showing rotation and identification of volcanic features with ephemeris overlays.
WR 137: Colliding-Wind Binary
WR 137 presents a challenging case due to a mirror tilt event between science and calibrator exposures. Method 2 (DISCO-based) successfully reconstructs the expected streak morphology of the dust plume, while Method 1 suffers from chromatic speckle artifacts due to PSF miscalibration. This demonstrates the utility of DISCOs for self-calibration in the presence of significant wavefront error.
Figure 6: WR 137 reconstructions before and after a mirror tilt event, highlighting the robustness of DISCO-based fitting to wavefront miscalibration.
Discussion and Implications
The results establish that forward-modeling in the image plane, combined with RML regularization, enables robust recovery of complex astrophysical scenes at the JWST diffraction limit, even in the presence of severe detector and wavefront systematics. The authors emphasize that, for most moderate-contrast targets, image plane modeling is preferable to Fourier-domain approaches, as the latter discard valuable information and are more sensitive to calibration errors. However, in cases of severe wavefront miscalibration, DISCO-based methods provide essential self-calibration.
The open-source dorito and amigo packages provide a modular, extensible platform for JWST interferometric data analysis, with applicability to a wide range of archival and future datasets. The authors recommend maximizing ramp groups (subject to BFE limits), matching calibrator and science target brightness, and employing subpixel dithering to disentangle detector effects.
Theoretical implications include the demonstration that RML imaging, while effective, is not optimal in all cases. The authors advocate for future work exploring alternative image bases (e.g., wavelets, shearlets) and machine learning-based priors (score-based, deep image priors, information field theory, autoencoders) to further enhance reconstruction fidelity, especially for high-contrast and coronagraphic observations.
Conclusion
This work provides a rigorous, data-driven framework for image reconstruction with the JWST Interferometer, overcoming key limitations of conventional interferometric analysis. The combination of differentiable forward modeling, RML regularization, and robust calibration strategies enables high-fidelity imaging across diverse astrophysical contexts. The open-source tools and methodological advances presented here will inform both the analysis of existing JWST data and the design of future high-angular-resolution astronomical instruments. The extension of these techniques to incorporate advanced priors and machine learning approaches represents a promising direction for further improvement in astronomical image reconstruction.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about making super-sharp pictures with the James Webb Space Telescope (JWST) using a special technique called interferometry. The team focuses on an instrument on JWST named NIRISS that can use a small mask with seven holes (the Aperture Masking Interferometer, or AMI). AMI can see very fine details, but its images were being blurred and distorted by detector quirks. The authors built new software tools (“amigo” and “dorito”) that learn how the telescope and detector behave and then use smart math to reconstruct clear, accurate images from the raw data.
Key Objectives
The paper sets out to do three main things in plain terms:
- Figure out why AMI’s images weren’t as sharp as expected.
- Build a method that models how the telescope and detector really work so they can “undo” problems and recover crisp pictures.
- Test the method on three very different targets to show it works: Jupiter’s volcanic moon Io, a dust-producing binary star system (WR 137), and a galaxy with an active black hole in its center (NGC 1068).
Methods and Approach
The problem in everyday language
Imagine taking a photo through a cardboard with seven small holes. The pattern of overlapping light from these holes contains hidden detail about the scene, like tiny stars or fine structures. AMI does this in infrared light. But JWST’s detector has a problem: when a pixel gets very bright, some charge “leaks” into neighboring pixels, making bright things look a bit puffier. This is called the “Brighter-Fatter Effect” (BFE). Because AMI’s images rely on precise patterns, even small non-linear distortions can mess up the details.
The solution: forward modeling and regularization
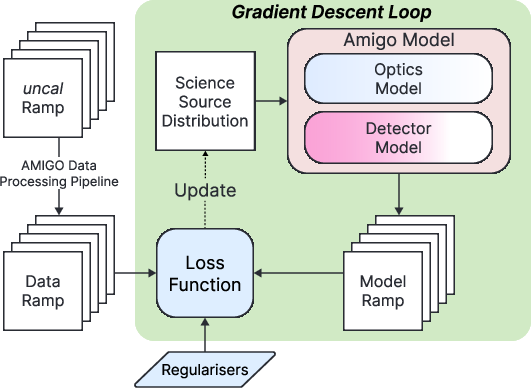
Rather than trying to “undo” the telescope data directly (which is very hard), the team uses “forward modeling.” Think of it like this: start with a guess of the true scene, pass it through a realistic, simulated JWST + detector pipeline, and compare the result to what JWST actually measured. Then nudge the guess to make it match better. Repeat until the simulated data and real data agree. This approach handles complicated physics and detector behavior.
Because many different images could fit the data, the team uses “regularization,” which is a set of gentle rules to prefer more natural-looking solutions. Two key regularizers are:
- Maximum Entropy: prefers images that don’t add unnecessary structure unless the data clearly demands it.
- Total Variation: prefers images with smooth regions and clean edges (like sharp borders), rather than noisy, wiggly patterns.
They implement all this in “dorito,” building on their differentiable instrument model “amigo.” “Differentiable” here means the software can automatically figure out how changes in the image or instrument parameters change the simulated data, which makes optimization fast and efficient. They also take advantage of GPUs (the kind of processors used in gaming) to speed things up.
Calibrating the optics with a reference star
Before reconstructing the science image, they first observe a nearby point-like star as a reference (a “PSF calibrator”). This tells them about tiny imperfections in the telescope’s mirrors and how the wavefront of light is distorted. They describe the distortions with standard shapes (Zernike polynomials), fix those in the model, and then apply the calibrated model to the science target.
Two reconstruction strategies
To improve readability, here are the two strategies they use:
- Method 1: Image-plane method
- They fit the image directly in the camera plane (the pixel data), modeling the detector and optics at the pixel level. This avoids tricky transformations and is very good when detector non-linearities (like the BFE) are the main issue.
- Method 2: DISCO method
- They first extract special interferometry measurements called “kernel-like” observables that are designed to ignore certain optical errors. Their version is called DISCO (Delay-Insensitive Subspace of Calibrated Observables). Then they reconstruct the image from these robust measurements. This is especially helpful if there are remaining wavefront errors, like sudden mirror segment changes.
Main Findings and Why They Matter
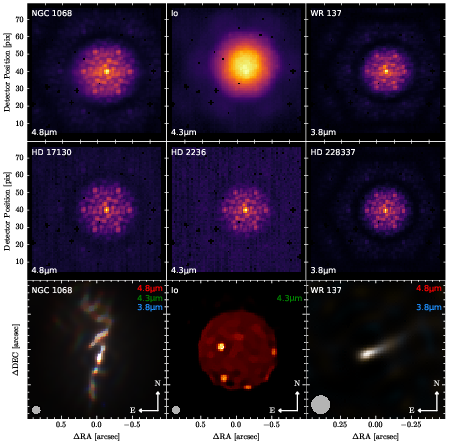
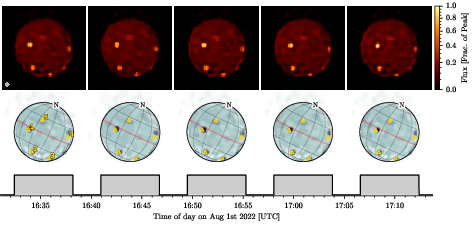
- Io (Jupiter’s moon):
- The reconstructions show a sharp disk with bright, well-resolved volcanic hotspots that move over about an hour. The edges of Io look crisp, and the hotspots match known volcano locations. This demonstrates that the method can handle extended objects with both smooth areas and tiny bright features.
- WR 137 (a colliding-wind binary with dust):
- They recover a narrow, elongated dust structure aligned with expectations from earlier work. During these observations, a “tilt event” moved a mirror segment, causing a mismatch between the calibrator and the science data. In this case, the DISCO method helped the reconstruction because it is more robust to wavefront errors. This shows the value of having two complementary methods.
- NGC 1068 (an active galaxy with a supermassive black hole):
- They recover structures consistent across three infrared filters, matching mid-infrared images taken by another instrument (LBTI). Getting consistent results across wavelengths is a strong sign of successful deconvolution. It means their approach can reveal detailed shapes in complex, bright, and dusty galactic centers.
Overall, their images reach JWST’s diffraction limit (the theoretical sharpness possible for its size and wavelength), and they can achieve good contrast over a wider field of view than older methods. That means more of the scene can be recovered clearly, and smaller, fainter features can be seen.
Implications and Potential Impact
This work shows a practical path to fix the main limitations that were holding back JWST’s AMI imaging. By accurately modeling the optics and detector and by using powerful, well-chosen regularization, astronomers can:
- Sharpen high-resolution images of complex targets like active galaxies, dusty binaries, and volcanically active moons.
- Better separate faint structures near bright sources, important for studying exoplanets, disks, and jets.
- Recover consistent details across multiple wavelengths, giving more confidence in the physical interpretation.
In short, these methods boost JWST’s ability to deliver the kind of ultra-fine infrared images that can answer big questions: how material flows around black holes, how stars and planets form in dusty environments, and how solar system bodies behave. The tools (amigo and dorito) are modular and scalable, so they can likely help with other telescopes or related imaging challenges in astronomy.
Knowledge Gaps
Below is a consolidated list of concrete knowledge gaps, limitations, and open questions that remain unresolved in the paper. Each item is phrased to guide future work toward actionable investigations or improvements.
- Detector Brighter-Fatter calibration ceiling: The effective detector model was trained only up to ~45% well depth (~30k counts), forcing ramp truncation. Extend calibration/training to higher counts to exploit full dynamic range and quantify reconstruction gains.
- Noise model fidelity: The likelihood assumes Gaussian errors, whereas up-the-ramp NIRISS data exhibit Poisson-Gaussian statistics with inter-group correlations and potential nonstationarity. Develop and compare physically accurate likelihoods (e.g., Poisson-Gaussian with correlated read noise and IPC).
- Uncertainty quantification: Reconstructions are MAP-only with Laplace approximations for visibilities; there is no posterior sampling or credible intervals for images. Implement HMC/NUTS over image and instrument parameters to propagate uncertainties into astrophysical inferences.
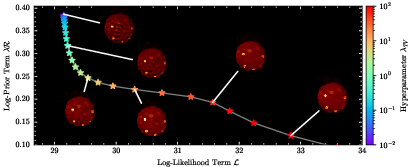
- Regularization choice and tuning: λ is selected heuristically (L-curve shown only for Io), with no standardized, automated criterion. Evaluate cross-validation, Bayesian evidence, or hierarchical priors for λ, and assess robustness across targets and filters.
- Regularizer/basis diversity: Reconstructions use MaxEnt, TV/QV in a pixel basis; sparsity in wavelet/shearlet bases and mixed-basis approaches are not explored. Benchmark alternative bases and regularizers against extended and point-like morphologies.
- Method selection criteria: The paper lacks quantitative diagnostics to decide between the image-plane (Method 1) and DISCO (Method 2) approaches. Design metrics (e.g., residual wavefront error, detector nonlinearity indicators) to select or blend methods adaptively.
- Wavefront calibration strategy: Science reconstructions hold calibrator-derived Zernike coefficients fixed; tilt events and temporal drift can invalidate this. Investigate joint wavefront+image inference for science frames and quantify sensitivity to calibrator mismatch.
- Pupil amplitude aberrations: The forward model and Jacobian ignore amplitude errors in the pupil. Determine whether amplitude aberrations measurably bias visibilities/images and extend the formalism to include amplitude terms.
- Spectral calibration and multi-band coupling: DISCO observables address spectral miscalibration, but spectral-model errors are not quantified and filters are reconstructed independently. Develop joint multi-band reconstructions with spectral regularization and validate against spectroscopy.
- Centroid constraint in DISCO fits: A tight prior forces the image centroid to the frame center, potentially biasing astrometry. Create centroid-invariant formulations or incorporate external astrometric constraints; quantify astrometric accuracy.
- Additional detector systematics: The scope of the effective detector model beyond BFE (e.g., IPC, persistence, nonlinearity, inter-group correlations) is unclear. Characterize and incorporate additional systematics; test across brightness and temperature regimes.
- Ramp vs slope modeling: Figures show slope images while methods claim up-the-ramp fitting; the treatment of group-to-group correlations and the comparative performance of slope-only vs full ramp modeling are not evaluated. Clarify and benchmark both approaches.
- Dithering and flux concentration: Undithered data exhibit flux concentration and require ad hoc Gaussian smoothing (σ≈0.25 pix). Quantify the impact of different dither strategies and replace smoothing with principled priors or sampling-based mitigation.
- Undersampled F277W band: Imaging at F277W is avoided due to undersampling. Investigate super-resolution strategies within the forward model (e.g., subpixel shifts, sparsity priors) to recover this band.
- Quantitative performance metrics: Claims of “consistent with the literature” lack standardized figures of merit (e.g., fidelity, dynamic range, contrast, inner working angle, residual maps). Define and report metrics; benchmark against AMICAL, SAMPip, ImPlaneIA, CLEAN, MPoL on identical datasets.
- Field-of-view and near-field effects: The asserted wider FOV relative to conventional interferometric limits is not quantified. Map reconstruction fidelity vs. off-axis angle, and characterize Fresnel defocus and mask non-conjugacy across the detector.
- Computational performance and scalability: No runtimes, memory footprints, GPU utilization, or scalability analyses are provided. Report computational costs for typical reconstructions and offer guidance on parameter counts and hardware requirements.
- Photometric fidelity: Source normalization and positivity constraints may bias absolute/relative photometry across filters. Validate photometric calibration against standards and quantify errors.
- Mixed parametric+pixel modeling: Targets with bright cores plus extended structures (NGC 1068, WR 137) may benefit from hybrid models (parametric core, pixel-based extended emission). Develop and test such models to stabilize reconstructions.
- Robustness to mirror tilt events: Only one tilt-event dataset is qualitatively discussed. Perform controlled tests to quantify Method 2’s mitigation, and implement automatic detection/flagging of tilt events in the pipeline.
- Temporal generalization of the base model: Mask metrology and electronic properties are held fixed; temporal variation is not modeled. Monitor and adapt these parameters per epoch or adopt online learning to maintain calibration fidelity.
- Synthetic truth validation: There are no end-to-end tests on realistic synthetic scenes with known ground truth under JWST-like noise/systematics. Add such benchmarks to quantify accuracy, bias, and failure modes.
- DISCO invariants domain of validity: The construction and limits of DISCO (e.g., sensitivity to defocus magnitude, Zernike truncation order, redundancy) are not mapped. Determine the conditions where DISCO remains invariant and its breakdown regimes.
- Reproducibility and workflow transparency: Code repos are cited, but complete, runnable workflows (configs, seeds, fits, outputs) for the three targets are not provided. Release fully reproducible pipelines and data products (e.g., via MAST/Zenodo).
- Backgrounds and stray light: Treatment of thermal/scattered backgrounds and stray light in NIRISS is not described. Model and subtract backgrounds within the forward model and quantify their impact.
- Propagating calibrator wavefront uncertainty: Covariance of calibrator-derived wavefront parameters is not propagated to science image uncertainties. Implement uncertainty propagation to image-level error bars.
- Zernike basis completeness per hole: The choice and order of Zernike polynomials across mask holes is unspecified; perform sensitivity analyses to basis order and parametrization choices.
- Fresnel defocus quantification: The magnitude and variability of near-field defocus are noted but not quantified. Establish calibration procedures to monitor defocus and assess its impact on invariants and reconstructions.
- Pixel grid and multi-resolution: The choice of reconstruction pixel scale and grid is not analyzed. Explore multi-resolution/adaptive grids and quantify effects on fidelity and computational cost.
Practical Applications
Immediate Applications
The following applications can be deployed now using the paper’s open-source tools (amigo for differentiable forward modeling and detector calibration; dorito for regularized maximum-likelihood image reconstruction; DISCO observables for self-calibrating Fourier-domain constraints), supported by demonstrated results on JWST/NIRISS AMI data (Io, WR 137, NGC 1068).
- Astronomy (space/ground-based interferometry)
- JWST/NIRISS AMI reprocessing for extended and high-contrast imaging
- Use
amigoto infer the wavefront from PSF calibrators (Zernike per hole); hold detector/mask parameters fixed to the trained base model; reconstruct science target imagery withdoritoin the image plane (Method 1) to overcome non-linear detector systematics (Brighter-Fatter Effect, BFE) and achieve near-diffraction-limited and wider-field reconstructions. - Sector: Software + Astronomy
- Tools/workflows:
amigobase model loading → calibrator wavefront fit → image-plane RML (max entropy,TV/QVregularization) → L-curve tuning → RGB-band fusion and validation against literature. - Assumptions/dependencies: Access to JWST AMI raw ramps; up-the-ramp data retained; base model trained/calibrated below ~45% full well (~30k counts); GPU resources; valid dither metadata; scene positivity enforced via log-parameterization; regularization hyperparameter selection (L-curve).
- Robust imaging in presence of significant wavefront error or tilt events
- Apply the
DISCOpipeline (Method 2) when PSF vary across calibrator/science or after “tilt events”: forward-model visibilities, build Jacobian with autodiff, derive kernel operator for phase modes (near-field, Fresnel defocus), diagonalize covariances, fit source distribution in the DISCO basis; mitigate wavefront sensitivity at low spatial frequencies. - Sector: Software + Astronomy
- Tools/workflows: Visibility fit → kernel operator via autodiff → DISCO transform + covariance propagation → centroid prior (tip/tilt invariance) →
doritoRML fit in DISCO space. - Assumptions/dependencies: Correct Jacobian generation; accurate Fresnel defocus modeling; covariance tracking and re-diagonalization; centroid priors to ensure convergence; amplitude errors not modeled in pupil; assumes Zernike basis captures dominant wavefront modes.
- Immediate science cases enabled or improved
- AGN torus/outflow morphology (e.g., NGC 1068): Cross-band, diffraction-limited reconstructions consistent with LBTI mid-IR morphology; supports comparative studies of fueling and feedback.
- Solar System volcanism (Io): High-fidelity mapping of thermal hotspots, resolved limb structure, temporal evolution over hour-long observations; complements Juno infrared characterization.
- Colliding-wind binaries (WR 137): Recover barely resolved dust structures (spiral plumes/streaks), improved robustness in adverse wavefront conditions.
- Sector: Academia (Astrophysics)
- Tools/workflows: Multi-filter imaging; cross-instrument comparisons (ALMA/LBTI/Keck AO); band combination; time-resolved reconstruction for rotation/variability.
- Assumptions/dependencies: Accurate spectral modeling per filter; reliance on PSF calibrators; stable up-the-ramp sampling; limited amplitude error modeling.
- High-contrast companion searches at the diffraction limit
- Extend
amigo+doritoto parametric + pixel hybrid reconstructions; reprocess archival AMI data (e.g., AB Dor AC, HD 206893) to refine contrasts/inner working angles beyond FFT-based pipelines. - Sector: Academia + Software
- Tools/workflows: Joint fits of discrete companions + extended emission; Bayesian optimization (Laplace or NUTS/HMC for uncertainties where feasible).
- Assumptions/dependencies: Detector non-linearity modeled; sufficient SNR; stable calibration across epochs.
- Observatory pipeline enhancement
- Integrate forward-modeling and RML reconstruction into JWST/NIRISS community workflows alongside AMICAL/SamPy/SAMPip; provide reproducible notebooks and GPU configs for batch reprocessing.
- Sector: Software + Policy (data processing standards)
- Tools/workflows: Containerized pipelines; MAST-linked recipes; open regularization presets (
MaxEnt,TV,QV) + L-curve selection; provenance tracking; public release of base models. - Assumptions/dependencies: STScI pipeline compatibility; community adoption; sustained maintenance and documentation.
- Education and training (computational imaging, astrostatistics)
- Course/lab modules on differentiable forward modeling and RML
- Use the paper’s datasets/workflows to teach autodiff-based Jacobian generation, regularization design, hyperparameter selection (L-curve), and uncertainty estimation.
- Sector: Education + Software
- Tools/workflows: JAX notebooks; GPU/CPU backends; hands-on reconstruction of Io/NGC 1068/WR 137; comparison of image-plane vs Fourier-plane methods.
- Assumptions/dependencies: Access to open-source code/data; student GPU resources or cloud credits.
- Industrial imaging and inspection (pilot/prototyping)
- Correcting non-linear CMOS artifacts (BFE-like effects) in lab/bench imaging systems
- Adapt
amigo-style effective detector modeling to characterize charge migration and non-linearities in machine vision cameras or microscopy detectors; prototype forward-model RML reconstruction for better edge preservation (TV) or smoothing (QV) depending on task. - Sector: Software + Robotics + Manufacturing
- Tools/workflows: Calibration dataset collection; detector neural net modeling; image-plane RML for deblurring and artifact suppression.
- Assumptions/dependencies: Availability of calibration sequences akin to up-the-ramp sampling; willingness to build instrument-specific forward models; compute resources.
Long-Term Applications
These applications require further research, scaling to new domains or instruments, generalization beyond JWST, or productization of the underlying methods.
- Cross-sector computational imaging platform
- A generalized, differentiable forward-model + RML SDK
- Productize
dorito/amigoconcepts into a cross-domain computational imaging SDK for Python (JAX/PyTorch) with plug-in instrument models (optics, detectors), regularizers (MaxEnt, TV/QV, wavelets/shearlets), and inference engines (gradient descent, HMC/NUTS). - Sector: Software
- Tools/products: “Computational Imaging SDK” with templates for cameras, telescopes, microscopes, and satellites; auto hyperparameter selection; covariance propagation; GPU-first design.
- Assumptions/dependencies: Instrument-specific forward-models; standardized calibration formats; open-source governance; sustained development funding.
- Medical imaging (MRI/CT/OCT/ultrasound)
- RML reconstructions with differentiable system models to correct non-linear systematics and sparse sampling artifacts
- Integrate TV/QV regularization (edge-preserving vs smoothing) and Bayesian priors into clinical reconstruction pipelines; apply kernel-like invariants where phase/amplitude paths are error-prone (e.g., OCT speckle).
- Sector: Healthcare
- Tools/workflows: Instrument forward models; clinical-grade validation; uncertainty quantification for diagnostics; real-time GPU recon with regulatory compliance.
- Assumptions/dependencies: Collaboration with device vendors; strict validation; privacy/compliance; high-throughput compute; evidence of clinical benefit.
- Satellite remote sensing and Earth observation
- Onboard or ground-based correction of detector non-linearities and optical aberrations for improved resolution/contrast in IR/VIS bands
- Use DISCO-like invariant observables to mitigate defocus/thermal drift; forward-model based deconvolution to sharpen features for environmental monitoring and urban analytics.
- Sector: Energy + Finance + Policy (environmental monitoring)
- Tools/workflows: Cal/Val campaigns; instrument thermal/optics models; batch reprocessing pipelines; QA metrics; change detection improved by better reconstructions.
- Assumptions/dependencies: Access to calibration telemetry; mission constraints; bandwidth/compute; model robustness to varied scenes.
- Robotics and autonomous systems (machine vision)
- Self-calibrating imaging pipelines under optical defocus and sensor non-linearities
- Embed kernel-invariant observables for robust feature extraction when optics deviate (vibration, temperature) and detectors exhibit charge migration; improve reliability in adverse conditions.
- Sector: Robotics
- Tools/workflows: Edge GPU implementations; sensor calibration routines; synthetic-to-real transfer learning with differentiable camera models.
- Assumptions/dependencies: Real-time constraints; robustness across environments; co-development with camera vendors.
- Instrument and mission co-design (optics + computation)
- Use differentiable forward models to optimize mask patterns, wavefront control, and detector readouts for future space/ground interferometers
- Jointly design hardware/software to maximize information recovery under practical constraints (sampling, BFE, Fresnel near-field effects).
- Sector: Academia + Space industry
- Tools/workflows: End-to-end simulations; gradient-based design optimization; sensitivity analyses; lab prototyping; flight pipeline alignment.
- Assumptions/dependencies: Access to design parameters; multi-party collaboration; validation against testbeds.
- Astronomical ecosystem extension
- Generalize
dorito/amigoto other instruments (NIRCam, MIRI, ground-based AMI/AO on ELT/TMT/GMT; LBTI-like mid-IR setups) - Build instrument-specific forward models and detector effective models; extend to undersampled bands (e.g., F277W) with super-resolution priors; integrate HMC/NUTS for credible intervals.
- Sector: Academia + Software
- Tools/workflows: Calibration campaigns; wavelet/shearlet bases for disks and extended features; uncertainty maps; cross-instrument joint inversions.
- Assumptions/dependencies: Sufficient calibration data; instrument metadata fidelity; compute scaling; community standards for uncertainty reporting.
- Generalize
- Industrial inspection and thermography
- Enhanced deconvolution and artifact correction in infrared thermography for energy audits and industrial monitoring
- Apply forward-modeled detector non-linearity correction and TV regularization to improve edge detection and thermal feature segmentation.
- Sector: Energy + Manufacturing
- Tools/workflows: Detector characterization kits; pipeline integration with thermography software; validation on controlled heat sources.
- Assumptions/dependencies: Calibration access; domain adaptation; operator training.
- Public policy and standards
- Guidelines for forward-model based calibration and reconstruction in large scientific missions
- Encourage archiving of calibration models (mask metrology, detector effective models) with data releases; set standards for uncertainty quantification and regularization disclosure.
- Sector: Policy
- Tools/workflows: Data standards; reproducibility checklists; funding support for open-source maintenance; community governance.
- Assumptions/dependencies: Agency buy-in (e.g., STScI/NASA/ESA); sustained community effort; interoperability with existing pipelines.
Notes on assumptions and dependencies common across applications
- Differentiable programming stack: Reliance on JAX (or PyTorch/TensorFlow) for autodiff, GPU acceleration, and Jacobian computation; access to modern GPUs or cloud resources.
- Calibration quality: Forward models require high-quality, instrument-specific calibration datasets; detector effective models must be trained across relevant operating ranges (not saturated).
- Regularization choice and tuning: Results depend on appropriate priors/regularizers (MaxEnt, TV/QV, wavelets) and sensible hyperparameter selection (e.g., L-curve).
- Domain generalization: Extending beyond JWST/NIRISS AMI requires developing new optical/detector models; DISCO invariants depend on accurate Jacobians and may not cover amplitude errors without extension.
- Data access and governance: Open-source sustainability and data-sharing practices (e.g., via MAST) affect reproducibility and community uptake.
Glossary
- Active Galactic Nucleus (AGN): A compact, extremely luminous region at a galaxy’s center powered by accretion onto a supermassive black hole. "NGC~1068 is a well-known \ac{agn} whose inner regions have recently been imaged in the mid-infrared \citep{Isbell25} using the \ac{lbti}."
- Aperture Masking Interferometer (AMI): An interferometric mode that uses a mask with multiple openings to create interference fringes for high-resolution imaging. "Flying on board the James Webb Space Telescope (JWST) above Earth's turbulent atmosphere, the \ac{ami} on the NIRISS instrument is the highest-resolution infrared interferometer ever placed in space."
- Aperture synthesis: Technique to reconstruct images by combining interference patterns from multiple sub-apertures to sample spatial frequencies. "Aperture synthesis is still possible in the presence of wavefront phase distortions by transforming the measured complex visibilities into data products that are less vulnerable to phase error."
- Angular differential imaging: High-contrast imaging strategy that exploits rotational diversity to distinguish astrophysical sources from quasi-static speckles. "— developed to reconstruct near-infrared circumstellar disk and exoplanet images in the context of high contrast angular differential imaging —"
- Brighter-Fatter Effect (BFE): Detector nonlinearity where charge migrates from bright pixels to neighbors, making bright features appear broader. "Charge diffuses from brighter pixels into neighbouring pixels, resulting in bright features appearing broader or fatter; hence this charge migration has been dubbed the \ac{bfe}."
- CLEAN method: Iterative deconvolution algorithm widely used in radio interferometry to remove the instrument’s PSF and reconstruct images. "An older but still widely used approach is the CLEAN method, which was designed to tackle interferometric data with sparse and irregular sampling of the - plane"
- Closure invariants: Self-calibrating interferometric quantities (e.g., closure phases) that are robust to certain wavefront errors. "While in general we show in this paper that closure invariants perform poorly for anchoring image reconstructions with jwst compared to image plane modelling, in this case we find that they significantly improve the deconvolution with significant wavefront error present."
- Closure phase: Sum of visibility phases around a baseline triangle that cancels certain phase errors, enabling robust detection of asymmetry. "Closure phases can therefore provide extremely accurate constraints on faint companions and asymmetric structure in images, even in the presence of systematic optical errors."
- Colliding-wind binary: A binary system where stellar winds collide, often producing dust structures observable via interferometry. "Colliding-wind binaries like \ac{wr137} \citep{WR1371985,WR1372001} produce spiral plumes of dust that were some of the first images to be resolved by aperture-masking interferometry \citep{Tuthill1999}."
- Delay-Insensitive Subspace of Calibrated Observables (DISCO): Self-calibrating interferometric observables constructed to be insensitive to wavefront and spectral miscalibration effects. "We refer to these observables as \acp{disco} to reflect that these are neither the previously-used kernel phase nor amplitude observables, as they include not just near-field effects but also spectral miscalibration."
- Dirty image: The direct inverse transform of sparsely sampled visibilities, containing sidelobe artifacts from incomplete sampling. "In radio astronomy, this resultant image is referred toas the ``dirty image''."
- Fizeau interferometry: Interferometric technique combining beams in the image plane using multiple apertures to form fringes. "The venerable technique of sparse aperture masking \citep[or Fizeau interferometry;] []{fizeau1868} blocks much of the telescope aperture, passing light only through a pattern of holes."
- Fresnel defocus: Near-field diffraction effect requiring a slight defocus in modeling when pupil and mask are not perfectly conjugate. "a small Fresnel defocus is required; this near-field effect means that the closure phases are no longer invariant."
- HAWAII-2RG CMOS detector: A specific infrared detector (CMOS-based) used in NIRISS, affected by BFE in these observations. "non-linear charge migration in \ac{niriss}' HAWAII-2RG \ac{cmos} detector"
- Inner working angle: The smallest angular separation at which an instrument can reliably detect features (e.g., companions). "with the consequence that the inner working angle and contrast limits of AMI were seriously compromised."
- Interferogram: The fringe pattern recorded on the detector from beam combination in an interferometric system. "in Fizeau interferometry as we do here, we refer to the fringe pattern on the detector as the interferogram."
- James Webb Space Telescope (JWST): Space-based infrared observatory providing stable, high-resolution imaging above Earth’s atmosphere. "Following its successful launch, the \ac{jwst} immediately established itself as the world's leading observatory for infrared astronomy."
- Kernel amplitude: The amplitude counterpart to kernel phase, forming self-calibrating observables in redundant apertures. "We therefore adapt the kernel phase and amplitude formalism \citep{kernel_phase,Pope_2013,kernel_amp}, which generalises closure invariants to redundant apertures:"
- Kernel operator: Null-space operator applied to visibilities to construct self-calibrating kernel observables that suppress phase error modes. "If we generate a null operator (also known as kernel operator) for the Jacobian matrix , we can use this to generate self-calibrating kernel phases"
- Kernel phase: Self-calibrating visibility phase combinations derived via a kernel operator to mitigate wavefront errors. "We therefore adapt the kernel phase and amplitude formalism \citep{kernel_phase,Pope_2013,kernel_amp}, which generalises closure invariants to redundant apertures:"
- L-curve: A diagnostic plot of data fit vs. regularization penalty used to select regularization strength. "L-curve diagram used to select the optimal regularisation parameter $\lambda_{\text{TV}$ for Io."
- Laplace approximation: Gaussian approximation to the posterior near its mode used to estimate parameter covariance. "by optimisation and then applying the Laplace approximation to estimate the covariance of these parameters \citep{Kass1991}."
- Large Binocular Telescope Interferometer (LBTI): Mid-infrared interferometer on the LBT used for high-resolution imaging of sources like NGC 1068. "NGC~1068 is a well-known \ac{agn} whose inner regions have recently been imaged in the mid-infrared \citep{Isbell25} using the \ac{lbti}."
- Mask metrology: Precise characterization of the aperture mask geometry used in forward modeling and calibration. "Here we allow the surface figures of mirrors and the parameters of astrophysical scenes to vary while holding the mask metrology and electronic properties fixed."
- Maximum Entropy (MaxEnt): Regularization that maximizes image entropy, favoring minimally informative images unless data demand structure. "This modular code by default includes regularisation by maximum entropy, and total variation defined with or metrics."
- NIRISS: JWST instrument (Near InfraRed Imager and Slitless Spectrograph) hosting the AMI mode. "Included in its suite of revolutionary instruments is the \ac{niriss}, hosting the Aperture Masking Interferometer \citep[AMI;] []{Sivaramakrishnan_2023} as one of its four observing modes."
- Non-Redundant Mask (NRM): Aperture mask with hole separations all unique, ensuring distinct baselines and better Fourier sampling. "The aperture mask, or \ac{nrm}, is a modest titanium disc small enough to fit into the \ac{niriss} pupil wheel perforated with seven holes in a non-redundant pattern to enable interferometric observations."
- Point spread function (PSF): The instrument’s response to a point source; convolved with the scene to form observed interferograms. "This pattern is the convolution of the \ac{psf} of the telescope with the source intensity distribution."
- Quadratic Variation (QV): Regularizer penalizing the squared magnitude of image gradients to encourage smoothness. "Quadratic variation, also known as total squared variation or quadratic smoothness, is the norm on the spatial gradient of the image."
- Ramp data / up-the-ramp: Detector readout strategy recording multiple groups as charge accumulates, enabling improved calibration. "By directly modelling pixel-level data as they accumulate up-the-ramp, amigo is able to sidestep the challenges of Fourier-plane calibration and improve upon the performance of the \hyperlink{https://jwst-docs.stsci.edu/jwst-science-calibration-pipeline}{\ac{jwst} pipeline} significantly."
- Regularized Maximum Likelihood (RML): Imaging approach combining a likelihood with regularization to solve ill-posed inverse problems. "In this paper, we document and apply \ac{rml} image reconstruction methods fitting to either the image plane or interferometric observables."
- Seyfert 2: A class of AGN observed at higher inclination, with obscured central engines and strong IR emission from dusty tori. "NGC~1068, or M77, is the prototypical Seyfert 2 \ac{agn} located at distance,"
- SUB80 sub-array: A specific NIRISS detector sub-array configuration used for AMI observations. "All observations were taken on NIRISS' SUB80 sub-array with the NISRAPID readout pattern."
- Tilt event: Sudden movement of a mirror segment changing the wavefront between calibrator and science observations. "there was a `tilt event' \citep{Schlawin2023,Lajoie2023} in which one of the mirror segments abruptly moved, so that the wavefront encountered by the \ac{psf} reference calibrator differs from that of the science target."
- Total Variation (TV): Regularizer penalizing the sum of gradient magnitudes, preserving edges while reducing noise and ringing. "Over-regularisation with total variation will result in an image with cartoonish features."
- u–v plane: Spatial frequency domain sampled by interferometric baselines; incomplete coverage leads to artifacts. "each telescope pairing will sample a different region of the - plane."
- Wavefront: The phase front of light across the pupil; distortions produce aberrations affecting the PSF and visibilities. "This \ac{psf} is the Fourier (or Fresnel) transform of the incoming wavefront, which typically experiences phase distortions — whether from the turbulent atmosphere or, even in space, from optical path delays from uneven or misaligned mirror surfaces."
- Wavefront error: Deviation of the actual wavefront from the ideal, introducing phase (and amplitude) errors in measurements. "Since \acp{disco} are invariant to Zernike tip/tilt modes by design, they are also invariant to translations in the image plane. This introduces a heavy covariance to the pixel parameters in the third stage fit, as there is zero constraint on the image centroid position. To assist convergence, a tight prior is added for the image centroid position to be at the image centre." [context: Method 2 is expected to be most effective when limited by residual wavefront error.]
- Zernike polynomials: Orthogonal polynomials on the unit disk used to parameterize wavefront aberrations. "We take the \ac{psf} reference star observed along the science target, and fit for the wavefront across each aperture with the trained amigo base model. This is parametrised as a set of Zernike polynomials across each hole of the aperture mask."
Collections
Sign up for free to add this paper to one or more collections.