Preconditioned Norms: A Unified Framework for Steepest Descent, Quasi-Newton and Adaptive Methods (2510.10777v1)
Abstract: Optimization lies at the core of modern deep learning, yet existing methods often face a fundamental trade-off between adapting to problem geometry and leveraging curvature utilization. Steepest descent algorithms adapt to different geometries through norm choices but remain strictly first-order, whereas quasi-Newton and adaptive optimizers incorporate curvature information but are restricted to Frobenius geometry, limiting their applicability across diverse architectures. In this work, we propose a unified framework generalizing steepest descent, quasi-Newton methods, and adaptive methods through the novel notion of preconditioned matrix norms. This abstraction reveals that widely used optimizers such as SGD and Adam, as well as more advanced approaches like Muon and KL-Shampoo, and recent hybrids including SOAP and SPlus, all emerge as special cases of the same principle. Within this framework, we provide the first systematic treatment of affine and scale invariance in the matrix-parameterized setting, establishing necessary and sufficient conditions under generalized norms. Building on this foundation, we introduce two new methods, $\texttt{MuAdam}$ and $\texttt{MuAdam-SANIA}$, which combine the spectral geometry of Muon with Adam-style preconditioning. Our experiments demonstrate that these optimizers are competitive with, and in some cases outperform, existing state-of-the-art methods. Our code is available at https://github.com/brain-lab-research/LIB/tree/quasi_descent
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper is about making training deep learning models faster, more stable, and easier to tune. The authors show that many popular training tricks (like SGD, Adam, Shampoo, Muon, SOAP, SPlus) are actually different faces of the same idea. They build one “big picture” that connects them, then use it to design two new optimizers, called MuAdam and MuAdam-SANIA, which perform very well in tests.
What questions are the authors asking?
In simple terms, they ask:
- Can we have the best of both worlds in training? That means:
- Flexibility to match the shape/structure of the model (geometry).
- Smart use of “curvature” (how the slope changes), which often makes training faster and more stable.
- Can we describe old and new optimizers using one shared recipe?
- When will an optimizer behave the same even if we change units (like meters to centimeters) or rotate/reshape the parameters? This is called invariance.
How did they approach the problem?
Think of training like hiking down a mountain to reach the lowest point (the best model). You choose:
- A direction to step (based on the gradient—where it slopes downward).
- How to measure distance and steepness (the “norm” or geometry).
- Whether to wear “special shoes” that reshape the ground to make downhill easier (that’s “preconditioning,” which uses curvature information).
The authors introduce “preconditioned norms,” which are like saying:
- We measure steepness after warping the space with certain matrices (L and R) or after scaling each position separately (D).
- Then we pick the direction that most reduces the loss under that warped measurement.
Key ideas explained:
- Gradient: The direction of steepest downhill slope right now.
- Norm (geometry): A rule for “how big” a step is. Different norms = different ways to measure steps.
- Preconditioning: A clever re-scaling of the problem so that downhill becomes smoother and faster.
- Steepest descent: Always step in the direction that most reduces loss given your chosen norm.
- Quasi-Newton methods: Use curvature information (second-order hints) to choose smarter steps.
- Adaptive methods (like Adam): Scale each parameter by its past behavior, so busy parameters step smaller and quiet ones step larger.
- Linear Minimization Oracle (LMO): A little “helper” that, given a budget for step size, picks the direction that helps the most under your chosen norm.
What the authors add:
- Two families of preconditioned norms:
- (L, R)-preconditioned norms: reshape rows and columns of a weight matrix before measuring step size (good for quasi-Newton-style methods).
- D-preconditioned norms: scale each element separately (good for Adam-style adaptive methods).
- A general result showing the LMO can be computed by transforming the gradient, using the base norm, and transforming back. This unifies many algorithms under one procedure.
What did they find?
1) A unified framework
They prove that many well-known optimizers are all special cases of their “preconditioned norms” idea:
- Steepest descent with different norms (e.g., spectral/Muon, sign-based methods).
- Quasi-Newton methods (e.g., K-FAC, Shampoo, SOAP).
- Adaptive methods (e.g., AdaGrad, Adam, SANIA).
- Hybrids (e.g., SOAP, SPlus).
This is powerful because it gives one recipe to design, compare, and improve optimizers.
2) Clear rules for invariance
They give exact conditions for when an optimizer:
- Is affine invariant: behaves the same after left/right linear changes to a weight matrix (like rotating or changing bases).
- Is scale invariant: behaves the same if you scale each weight/feature separately (like changing units).
These are practical: the rules say how the preconditioners (L, R, or D) should transform so the optimizer’s behavior stays consistent.
3) Two new optimizers: MuAdam and MuAdam-SANIA
- MuAdam: Combines Muon’s spectral geometry (it focuses on the most “influential directions” of a weight matrix) with Adam-style adaptive scaling.
- MuAdam-SANIA: Same idea, but with SANIA’s scaling (which is scale-invariant), making it robust to unit changes.
Why spectral geometry helps: It pays attention to how a matrix (layer weights) affects inputs overall, not just element by element. This often gives more stable, meaningful steps for matrix-shaped layers.
4) Experiments show strong results
They test on:
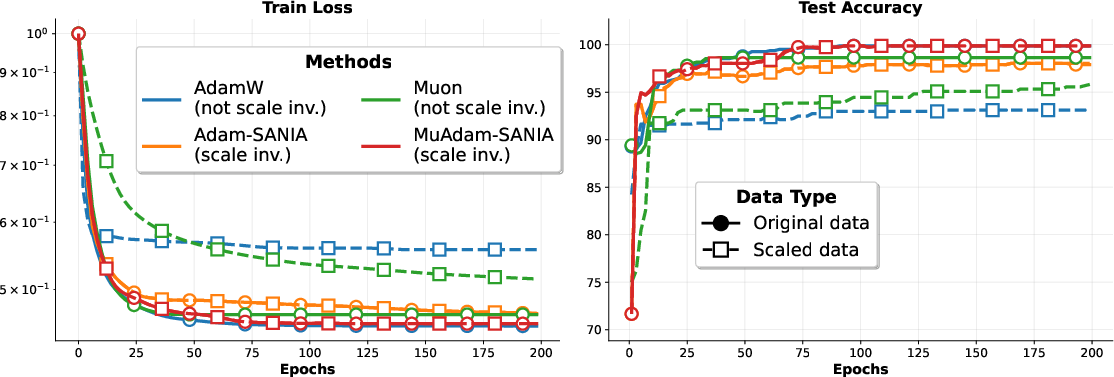
- Scale invariance (Mushrooms dataset): Methods without scale invariance (AdamW, Muon) suffer when features are rescaled; MuAdam-SANIA stays steady, as expected.
- GLUE (language tasks with DistilBERT): MuAdam is competitive and often matches or beats strong baselines.
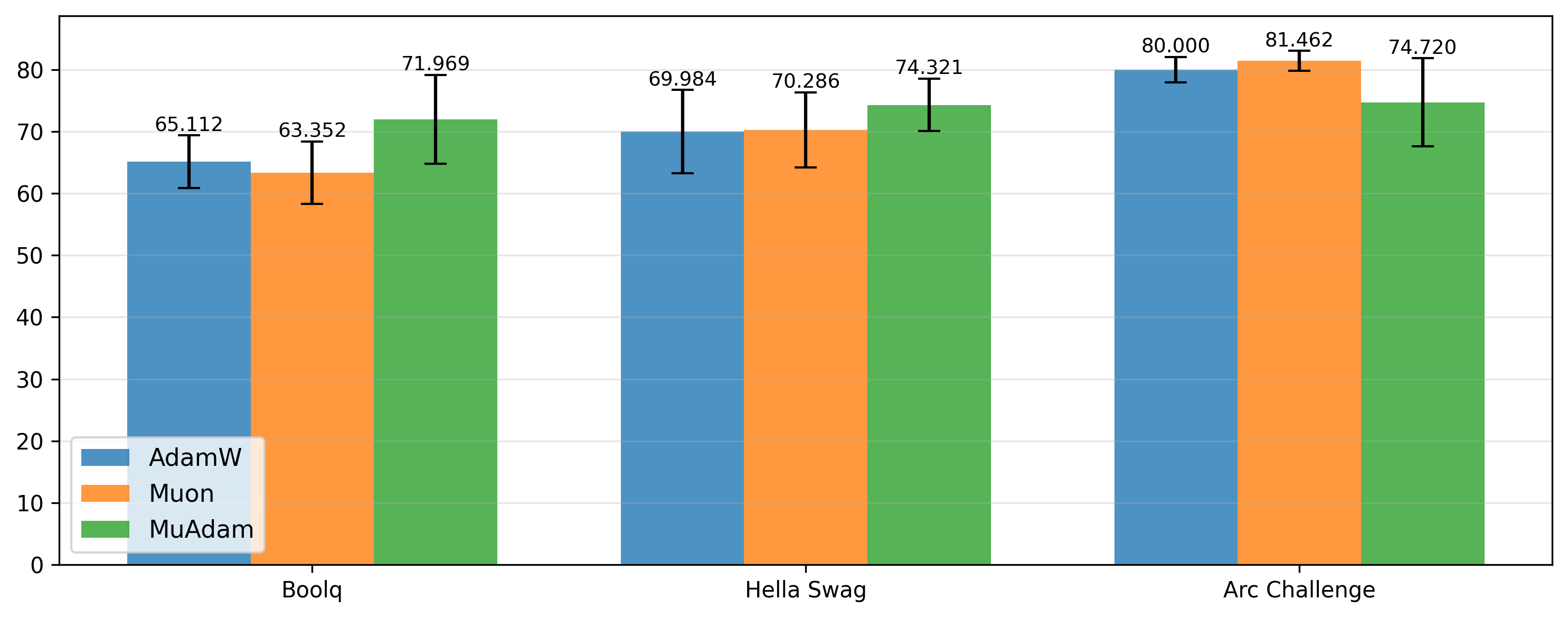
- LLM fine-tuning (Qwen2-7B on BoolQ, HellaSwag, ARC-Challenge): MuAdam is strong on two of three tasks.
- Character-level language modeling (Shakespeare): MuAdam usually edges out AdamW and clearly beats Muon.
Overall, their new methods are competitive or better than popular baselines in several settings.
Why is this important?
- One framework to reason about many optimizers makes it easier to understand why they work, when to use them, and how to combine their strengths.
- Invariance means less headache tuning hyperparameters when data or layers are represented differently (e.g., different units, bases, or scales). This can save time and reduce training failures.
- The new optimizers (MuAdam, MuAdam-SANIA) show that mixing spectral geometry with adaptive scaling is practical and effective.
What’s the impact and what comes next?
This work gives a “toolbox” for designing better optimizers:
- You can pick a geometry (how you measure steps) and a preconditioner (how you reshape the problem), then combine them systematically.
- The invariance rules help you build optimizers that are robust to common changes in data and model design.
- The promising results suggest that many unexplored combinations might perform even better, especially for large models like LLMs.
In short: the paper unifies many training methods under one simple idea (preconditioned norms), proves when they’re robust to changes, and introduces new optimizers that work well in practice.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of concrete gaps and open problems left unresolved by the paper that future work could address:
Theoretical foundations
- Lack of convergence guarantees: no global/local convergence rates (convex or nonconvex), stationarity guarantees, or regret bounds for LMO steps under the proposed preconditioned norms in stochastic settings.
- Missing descent and stability analysis: no conditions under which the preconditioned LMO step is a descent direction, nor stability guarantees under stochastic gradients and momentum.
- Invariance results hinge on uniqueness: the affine/scale invariance theorems assume a unique LMO solution; many norms (e.g., spectral norm with repeated top singular values, sign-based norms) yield non-unique solutions. There is no treatment of tie-breaking, randomized selection, or robustness of invariance under non-uniqueness.
- Invariance with momentum and bias correction: the paper includes momentum and bias correction (Adam-style) in Algorithm 1 but does not analyze whether these modifications preserve the stated invariance properties beyond the special SANIA case with ε=0.
- Impact of ε > 0 on invariance: scale invariance of MuAdam-SANIA is shown only for ε=0, whereas practical implementations require ε>0; bounds quantifying invariance-breaking due to ε are missing.
- Conditions for simultaneous invariances: necessary and sufficient conditions are provided separately for affine (L,R) and scale (D) invariance, but the compatibility (or impossibility) of achieving both simultaneously in the matrix setting remains unaddressed.
- General base norms: Theorem 1 covers general base norms abstractly, but computability and properties (e.g., smoothness, duality, Lipschitz constants) required for LMO tractability and convergence are not specified for many α→β norms.
- Relation to mirror/natural gradient: no formal connection to mirror descent, Bregman divergences, or natural gradient methods, despite the heavy emphasis on geometry and invariance.
- Quasi-Newton interpretation limits: while unification is claimed, there is no rigorous equivalence proof (beyond Frobenius geometry) connecting the proposed preconditioned norms to known quasi-Newton updates (e.g., exact conditions when the LMO update replicates a quasi-Newton step).
- Proof completeness: parts of the appendix proofs are truncated/incomplete; full technical details for Theorem 1/Theorem 2 conditions and edge cases are not fully documented.
Algorithmic design and analysis
- Spectral LMO approximation accuracy: no error bounds or iteration/time complexity guarantees for the Newton–Schulz spectral LMO, nor sensitivity to gradient conditioning or choice of iterations/tolerance.
- Double preconditioning in Algorithm 1: the necessity and quantitative benefit of applying the element-wise preconditioner both before and after the spectral LMO (lines “First preconditioning” and “Second preconditioning”) are not theoretically justified or empirically ablated.
- Choice of exponent p: setting p=1/4 (Adam) and p=1/2 (SANIA) is adopted from prior methods without analysis; no theory or ablation shows how p affects invariance, conditioning, convergence, or generalization.
- Handling non-uniqueness in Muon/SPlus LMOs: the spectral LMO (Muon) and sign-based LMO (SPlus) can be non-unique; the paper does not specify deterministic tie-breakers or assess the impact on convergence and invariance.
- Extension beyond matrices: the framework targets matrix parameters; many DL parameters are tensors (conv kernels, attention tensors). How to generalize preconditioned norms and invariance to tensor operators is left open.
- Integration with regularization: interactions with decoupled weight decay (AdamW), gradient clipping, and other common training tricks are not analyzed within the invariance framework.
- Robustness to heavy-tailed noise and non-smooth losses: no analysis of behavior under gradient noise with heavy tails or non-smooth objectives, which are common in modern training regimes.
Computational and systems aspects
- Computational overhead: no wall-clock or FLOP/byte breakdown comparing MuAdam/MuAdam-SANIA to AdamW, Muon, Shampoo, SOAP, or SPlus; absent is a cost–accuracy trade-off analysis.
- Memory footprint: no analysis of memory overhead for maintaining Vt and performing spectral LMO per layer, especially for large models; memory–speed trade-offs and feasible approximations are not explored.
- Distributed/mixed-precision training: no discussion of how the spectral LMO and double preconditioning interact with data/model parallelism, communication costs, mixed precision, and numerical stability across devices.
- Scalability to large pretraining: empirical results are limited to fine-tuning (GLUE, LLM LoRA) and small-scale tasks (Shakespeare, Mushrooms); no evidence on large-scale pretraining (e.g., ImageNet pretraining, LLM full training) where second-order methods often show gains.
Empirical evaluation gaps
- Limited baselines: comparisons omit strong hybrid/second-order baselines (Shampoo, KL-Shampoo, K-FAC, SOAP, SPlus) on the same tasks; claims of competitiveness lack head-to-head evaluations with these methods.
- Scope of MuAdam-SANIA evaluation: MuAdam-SANIA is only tested in the scale invariance experiment; its performance on GLUE/LLM/vision tasks is not reported.
- Hyperparameter fairness: tuning strategies differ across experiments (Optuna vs. learning-rate-only sweeps), with few seeds in some settings; fair, compute-matched hyperparameter sweeps and robust aggregation across seeds are missing.
- Wall-clock and throughput: no reporting of training throughput, time-to-target, or efficiency under equal compute budgets—critical to justify added complexity of spectral LMOs.
- Ablations: missing ablations on (i) number of Newton–Schulz iterations/tolerance, (ii) presence/absence of the second D preconditioning, (iii) momentum and bias-correction effects, (iv) ε magnitude, and (v) p choices.
- Domain breadth: no evaluation on standard vision benchmarks (e.g., ImageNet, CIFAR), speech, or reinforcement learning—domains where curvature-aware methods often differ in efficacy.
- Generalization diagnostics: no analyses of sharpness, Hessian spectra, or calibration; it remains unclear whether the proposed geometry affects generalization beyond task accuracy.
- High learning rate robustness: claims about stability at high learning rates are not systematically tested (e.g., LR stress tests, divergence rates, recovery from instabilities).
Practical usability and design guidance
- Norm selection guidance: no practical criteria for choosing the base norm (spectral vs. other α→β norms) per layer/architecture; automatic norm selection or adaptive geometry choice is not addressed.
- Layer-wise/tensor-wise design: no guidelines for applying spectral LMO to convolution kernels (reshape vs. direct tensor operators), attention matrices, or low-rank adapters (LoRA), nor analysis of how these choices impact invariance.
- Preconditioner construction under constraints: how to build L, R, or D that satisfy invariance transformation rules given running estimates (EMA, clipping, damping) is not operationalized for practitioners.
- Numerical stability: no investigation of conditioning and numerical issues in Newton–Schulz with preconditioned inputs, sensitivity to scaling, or failure modes under extreme gradients.
Conceptual and methodological extensions
- Joint invariance and curvature: feasibility of designs that achieve both affine and scale invariance while leveraging curvature (beyond trivial cases) is not explored.
- Learning the geometry: the possibility of learning or adapting the base norm or preconditioners online (meta-optimization) is not considered within the framework.
- Bridging to information geometry: whether the preconditioned norms approximate Fisher geometry or natural gradient in any limit remains unexplored.
- Task- and layer-adaptive composition: the framework suggests a large design space (composing L,R with D and diverse base norms), but systematic exploration and principled selection heuristics are not provided.
Practical Applications
Practical Applications of “Preconditioned Norms: A Unified Framework for Steepest Descent, Quasi-Newton and Adaptive Methods”
This paper introduces a unifying framework for matrix-parameterized optimization using preconditioned norms, rigorously characterizes affine and scale invariance, and proposes two deployable optimizers (MuAdam and MuAdam-SANIA) that blend spectral-geometry LMOs with adaptive preconditioning. Below are concrete, real-world applications derived from the paper’s findings, methods, and innovations.
Immediate Applications
- Drop-in optimizer replacement for deep learning training and fine-tuning
- Sector: software/AI, healthcare, finance, education, robotics, energy
- What: Replace AdamW/Muon with MuAdam or MuAdam-SANIA in PyTorch/TensorFlow/JAX training loops to improve stability, reduce sensitivity to feature scaling, and match or exceed baseline performance (validated on GLUE, LLM LoRA fine-tuning, and character-level language modeling).
- Tools/Workflows: torch.optim.MuAdam, Hugging Face Trainer callback, Lightning strategy plugin; code from the paper’s GitHub.
- Assumptions/Dependencies: Accurate and stable Newton–Schulz iteration for spectral LMO; matrix-shaped parameter mapping for layers (reshape conv kernels/LoRA matrices); potential epsilon trade-off in SANIA (ε=0 gives exact scale invariance but may need ε>0 for numerical stability).
- Stable and robust LoRA fine-tuning at higher learning rates
- Sector: software/AI (LLMs), education-tech, enterprise NLP
- What: Use MuAdam for LoRA fine-tuning of transformer models (e.g., Qwen2-7B) to achieve competitive or better accuracy with improved stability and reduced hyperparameter sensitivity.
- Tools/Workflows: LoRA adapters + MuAdam; learning-rate sweeps with fewer trials due to invariance; CI recipes for model personalization.
- Assumptions/Dependencies: Spectral LMO overhead must be amortized by improved convergence; ensure batched matrix multiplies are efficient on target hardware (GPU/TPU).
- Reduced data preprocessing burden via scale-invariant training
- Sector: healthcare (EHR), finance (tabular time series), industrial IoT
- What: Use MuAdam-SANIA to reduce or eliminate manual feature rescaling/standardization for ill-conditioned inputs; training becomes less sensitive to coordinate-wise scaling (empirically verified on Mushrooms dataset).
- Tools/Workflows: Swap optimizer + simple scaling stress-test harness to validate invariance on your dataset.
- Assumptions/Dependencies: Exact scale invariance assumes ε→0; in production ε>0 typically used—expect near-invariance; ensure stable EMA configuration.
- Faster optimizer selection and fewer hyperparameter sweeps in AutoML
- Sector: AutoML/MLOps
- What: Because invariance reduces sensitivity to data and parameter reparametrizations, AutoML pipelines can narrow the search grid (learning rates, weight decay), speeding iteration.
- Tools/Workflows: Integrate MuAdam/MuAdam-SANIA as default candidates; “invariance-aware” AutoML templates.
- Assumptions/Dependencies: Benefits depend on task variability and the extent of feature/architecture heterogeneity.
- Invariance diagnostics for optimizer evaluation
- Sector: academia, MLOps/QA
- What: Add invariance unit tests (affine/scale stress tests) to model/optimizer validation to catch instability early and standardize optimizer benchmarking.
- Tools/Workflows: “Invariance profiler” in CI: data rescaling, basis changes, and layer reparameterization checks; adopt paper’s definitions/conditions for invariance.
- Assumptions/Dependencies: Requires reproducible pipelines and standardized protocols for rescaling/transformations.
- Training stability for on-device and edge learning with heterogeneous sensors
- Sector: robotics, embedded/IoT
- What: Apply scale-invariant MuAdam-SANIA to mitigate sensor-scale heterogeneity during on-device fine-tuning or continual learning (less error from device-to-device scaling).
- Tools/Workflows: Lightweight model adapters (LoRA) + MuAdam-SANIA; avoid extensive per-device normalization.
- Assumptions/Dependencies: Compute/memory footprint must fit edge constraints; Newton–Schulz iteration count may need to be reduced on constrained hardware.
- Improved robustness in classical tabular ML pipelines
- Sector: finance, insurance, operations
- What: Drop-in use of MuAdam-SANIA in deep tabular models where feature scaling is irregular across sources; reduce time spent on feature engineering.
- Tools/Workflows: Tabular DL frameworks (e.g., FT-Transformer) with MuAdam-SANIA; standardized data-ingestion with minimal normalization.
- Assumptions/Dependencies: Benefit size depends on current data hygiene and model architecture.
- Teaching and curriculum updates in optimization and deep learning
- Sector: academia/education
- What: Use the unified framework to teach how SGD, quasi-Newton (Shampoo/K-FAC), adaptive (Adam), and hybrids (SOAP/SPlus) arise from preconditioned norms; design lab assignments showing invariance conditions.
- Tools/Workflows: Lecture notes and code labs with lmo_base + preconditioners; compare optimizer behaviors under controlled reparametrizations.
- Assumptions/Dependencies: Students need access to GPU resources for spectral LMO experiments.
- Research baselines and ablation studies across architectures
- Sector: academia/industrial research
- What: Adopt MuAdam/MuAdam-SANIA and the framework’s LMO formulations as standard baselines in papers exploring optimizer behavior, geometry, or curvature use.
- Tools/Workflows: Add “geometry × preconditioner” ablation matrices; include SOAP/SPlus/MuAdam variants from the paper’s unification table.
- Assumptions/Dependencies: Ensure fair compute accounting since LMOs/preconditioners differ in cost.
- Production training cost and energy reductions through convergence and stability gains
- Sector: software/AI, cloud platforms
- What: Leverage improved stability/robustness to maintain higher learning rates or fewer restarts, thus cutting training time and energy.
- Tools/Workflows: Optimizer selection policies in training orchestration; energy/CO2 dashboards attribute savings to optimizer choice.
- Assumptions/Dependencies: Realized savings depend on model size, batch size, hardware throughput, and training schedule.
- Plugin for “optimizer composer” in frameworks
- Sector: software tooling
- What: Provide a UI/API to compose base norms (spectral/Frobenius/operator norms) with preconditioners (Kronecker/diagonal) and LMOs (sign/spectral) to quickly prototype new optimizers.
- Tools/Workflows: PyTorch/JAX extension; config-driven optimizer graphs; use Theorem 1 (LMO under transformations) to wire components correctly.
- Assumptions/Dependencies: Requires careful numerical safeguards and automatic scaling for Newton–Schulz convergence.
- Better personalization and fine-tuning in consumer AI apps
- Sector: consumer apps/daily life
- What: Faster, more stable small-scale fine-tuning (e.g., custom assistants, domain-specific summarizers) with fewer failed runs and less tuning effort.
- Tools/Workflows: App-level “personalize with MuAdam” button; background LR sweep minimized.
- Assumptions/Dependencies: Gains vary by model and personalization data size/quality.
Long-Term Applications
- Optimizer auto-design (“optimizer search”) powered by the unified framework
- Sector: AutoML, research tooling
- What: Automated exploration of the design space: base norms × (L,R) preconditioners × D-preconditioners × LMO choices; task-specific optimizer synthesis.
- Tools/Workflows: NAS-style optimizer search; meta-learning of geometry and preconditioning schedules.
- Assumptions/Dependencies: Compute-intensive; needs robust scoring/regularization to avoid overfitting to benchmarks.
- Hardware co-design for LMOs and preconditioned norms
- Sector: semiconductor/accelerators
- What: Add primitives for Newton–Schulz iterations, batched operator norms, and Kronecker factorizations in GPUs/TPUs/NPUs to accelerate generalized LMOs.
- Tools/Workflows: Kernel libraries (CUDA, ROCm, XLA) and sparsity-friendly matmul; hardware-aware optimizer implementations.
- Assumptions/Dependencies: Requires vendor adoption; careful evaluation of cost–benefit vs standard Adam kernels.
- Invariance-aware training standards and benchmarks
- Sector: policy, industry consortia, reproducibility initiatives
- What: Establish guidelines to report optimizer invariance (affine, scale) and energy/convergence metrics; standardize data-rescaling stress tests.
- Tools/Workflows: Shared benchmark suites; reporting checklists; MLPerf-style tracks for invariance.
- Assumptions/Dependencies: Community buy-in; clear definition of acceptable ε and numerical tolerances.
- Federated and multi-tenant training with heterogeneous feature scales
- Sector: mobile/edge/federated learning
- What: Use scale-invariant optimizers to mitigate client heterogeneity (device-specific scaling), improving aggregation stability and fairness.
- Tools/Workflows: Federated averaging with MuAdam-SANIA on clients; invariance diagnostics at the server.
- Assumptions/Dependencies: Communication and privacy constraints; heterogeneity may extend beyond scaling (e.g., label shift).
- Robust optimization under distribution and representation shifts
- Sector: safety-critical AI (healthcare, autonomous systems)
- What: Exploit invariance to reduce brittleness under representation changes (sensor calibrations, feature units), complementing robustness training.
- Tools/Workflows: Robust training pipelines that combine invariant optimizers with data augmentation and uncertainty estimation.
- Assumptions/Dependencies: Invariance is not a substitute for full distributional robustness; need broader robustness strategies.
- Cross-modal and layer-wise geometry selection
- Sector: multimodal AI, foundation models
- What: Assign different base norms per layer/module (e.g., spectral for attention weights, Frobenius for embeddings) to match local geometry, guided by the framework.
- Tools/Workflows: Per-layer optimizer composer; automated geometry assignment via curvature/gradient statistics.
- Assumptions/Dependencies: Requires profiling tools and heuristics; incremental rollout to control complexity.
- Training at scale for foundation models
- Sector: large-scale AI pretraining
- What: Explore whether hybrid LMOs with structured preconditioning can stably support larger learning rates, reduce warmup, and decrease total steps.
- Tools/Workflows: Large-cluster training with MuAdam/SOAP/SPlus-like hybrids; schedule and precision co-tuning.
- Assumptions/Dependencies: Empirical validation at 10B–100B+ scales; careful memory and communication budgeting.
- Low-precision and compressed training compatibility
- Sector: systems/efficiency
- What: Combine spectral-LMO-based updates with quantization or low-rank adapters (LoRA) to maintain stability at lower precision.
- Tools/Workflows: FP8/BF16 training with mixed-precision LMOs; quantization-aware optimizer kernels.
- Assumptions/Dependencies: Sensitivity of Newton–Schulz to low precision; needs error-compensation strategies.
- Domain-specific optimizer presets and “recipes”
- Sector: vertical AI solutions (bioinformatics, climate, recommendation)
- What: Package geometry–preconditioner combinations tuned for domain architectures and data (e.g., Kronecker-based for vision backbones, spectral+SANIA for transformers).
- Tools/Workflows: Cookbook repositories and config presets; MLOps templates per sector.
- Assumptions/Dependencies: Domain-dependent validation; keep recipes updated with evolving architectures.
- Extended theory and methods for tensors and structured layers
- Sector: research
- What: Generalize preconditioned norms and invariance conditions to tensor-parameterized models (e.g., convolution kernels, factorized layers), and to RL and control.
- Tools/Workflows: Tensor-operator LMOs; invariance in manifold/structured optimization.
- Assumptions/Dependencies: New math and efficient kernels; proof techniques for uniqueness and stability.
- “Invariance profiler” and compliance tooling for enterprises
- Sector: governance, risk, and compliance (GRC)
- What: Tools that audit training pipelines for invariance properties and generate compliance artifacts (e.g., sensitivity to reparametrization).
- Tools/Workflows: CI integration; dashboards showing invariance scores over time and across releases.
- Assumptions/Dependencies: Clear acceptance thresholds; mapping invariance metrics to business risk.
- Adaptive curricula that change geometry over training
- Sector: research/AutoML
- What: Schedules that start with one geometry (e.g., spectral) and gradually blend in/away from preconditioning as curvature estimates mature.
- Tools/Workflows: Geometry schedulers; progression rules tied to gradient anisotropy metrics.
- Assumptions/Dependencies: Require robust phase-change criteria; avoid destabilizing transitions.
Notes on feasibility and dependencies across applications:
- Numerical stability: Theoretical invariance results often assume exact conditions (e.g., ε=0, unique LMO solution). Production systems typically set ε>0 and approximate LMOs (Newton–Schulz with few iterations), yielding near-invariance.
- Compute overhead: Spectral LMOs introduce additional matrix multiplications. Gains must outweigh costs (often true when they reduce restarts or tuning).
- Layer shapes: Mapping tensors to matrices (and back) must be consistent for spectral LMOs; reshaping conventions matter for convs and attention.
- Hardware: Benefits improve with efficient matmul kernels and batched operations; specialized kernels could further accelerate LMOs.
- Generality: Empirical evidence is promising across NLP and language modeling tasks; broader validation is needed on vision, speech, and large-scale pretraining.
Glossary
- AdaGrad: An adaptive optimization algorithm that uses accumulated squared gradients to scale updates per parameter. "AdaGrad \citep{duchi2011adaptive}"
- Adaptive optimizers: Methods that adjust learning rates per parameter using gradient statistics, often achieving scale invariance. "adaptive optimizers incorporate curvature information but are restricted to Frobenius geometry"
- Affine invariance: A property where optimization dynamics are unchanged under linear reparameterizations of parameters. "the so-called affine invariance \citep{nesterov1994interior, nesterov2018lectures, d2018optimal}"
- ARC-Challenge: A benchmark dataset for complex multiple-choice reasoning. "ARC-Challenge \citep{clark2018think}"
- Adam: An adaptive optimizer combining momentum and per-parameter scaling via exponential moving averages of gradients and squared gradients. "Adam \citep{kingma2014adam}"
- Adam-SANIA: A variant of Adam using SANIA-style normalization for scale invariance. "Adam-SANIA \citep{abdukhakimov2023sania}"
- BoolQ: A yes/no question answering dataset used for evaluating reading comprehension. "BoolQ \citep{clark2019boolq}"
- CoLA: The Corpus of Linguistic Acceptability task in GLUE, evaluated with Matthews correlation. "Matthews correlation for CoLA"
- DistilBERT: A compact transformer model used for fine-tuning on NLP benchmarks. "We fine-tune DistilBERT base on GLUE tasks \citep{wang-etal-2018-glue}"
- Exponential moving average (EMA): A running average that gives exponentially decreasing weights to older observations. "EMA indicates that the exponential moving average of the corresponding quantity is utilized."
- Frobenius geometry: Optimization geometry based on the Frobenius norm, often assumed by quasi-Newton and adaptive methods. "restricted to Frobenius geometry"
- Frobenius inner product: The sum of element-wise products of two matrices, used as the inner product in matrix spaces. "\langle \cdot,\cdot\rangle denotes the Frobenius inner product."
- Frobenius norm: The square root of the sum of squared matrix entries; a common base norm for matrix optimization. "includes adaptive optimizers with Frobenius base norm"
- GLUE: A benchmark suite of NLP tasks for evaluating LLM performance. "GLUE tasks \citep{wang-etal-2018-glue}"
- Hadamard product: Element-wise multiplication of matrices. "\odot denotes the Hadamard product"
- HellaSwag: A commonsense reasoning benchmark with multiple-choice sentence completion. "HellaSwag \citep{zellers2019hellaswag}"
- Hessian: The matrix of second derivatives of the loss, encoding curvature information. "estimates the Hessian \nabla2 \mathcal{L}(W_t)"
- K-FAC: Kronecker-Factored Approximate Curvature; a layer-wise second-order optimizer using Kronecker factorizations. "K-FAC \citep{martens2015optimizing}"
- KL-Shampoo: A variant of Shampoo incorporating KL-based updates or regularization. "KL-Shampoo"
- Kronecker product: A tensor product between matrices used to build large structured curvature approximations. "their Kronecker product acts as a surrogate Hessian "
- Kronecker-factored preconditioning: Curvature approximation using Kronecker products of smaller factors for scalability. "are representative of the widely used Kronecker-factored preconditioning family \citep{martens2015optimizing,zhang2025concurrence}"
- Kronecker structure: The use of Kronecker products to structure curvature approximations in matrix-parameterized models. "via the Kronecker structure "
- Linear Minimization Oracle (LMO): A procedure that returns the direction maximizing inner product with the gradient under a norm constraint. "the update step is written in terms of a Linear Minimization Oracle (LMO)"
- LoRA: Low-Rank Adaptation; a parameter-efficient fine-tuning method for large models. "We evaluate both LoRA and full fine-tuning"
- MADGRAD: An adaptive optimizer variant that uses different exponent rules for preconditioners. "MADGRAD \citep{defazio2022momentumized}"
- Matthews correlation: A balanced metric for binary classification, used for CoLA in GLUE. "Matthews correlation for CoLA"
- MuAdam: A hybrid optimizer combining Muon’s spectral LMO with Adam-style diagonal preconditioning. "MuAdam"
- MuAdam-SANIA: A Muon-based optimizer with SANIA preconditioning to achieve scale invariance. "MuAdam-SANIA"
- Muon: A spectral steepest descent optimizer using the matrix spectral norm geometry. "Muon \citep{jordan2024muon}"
- Newton–Schulz iteration: An iterative method to approximate matrix inverses or projections using only multiplications. "via Newton–Schulz iteration \citep{bernstein2024old}"
- Operator norms (α→β): Matrix norms induced by vector norms, measuring the worst-case amplification from one normed space to another. "A general and widely studied family is given by the operator norms:"
- Preconditioned matrix norm: A matrix norm defined after applying a transformation (preconditioner) to encode geometry or curvature. "preconditioned matrix norms"
- Qwen2-7B: A 7-billion-parameter LLM used for fine-tuning experiments. "Qwen2-7B"
- Quasi-Newton methods: Optimization methods that use curvature approximations to adjust update directions without computing full Hessians. "quasi-Newton methods approximate curvature by introducing a positive definite matrix "
- RMS norm: The root-mean-square vector norm used to define certain operator/matrix norms. "rootâmeanâsquare norm"
- RMSProp: An adaptive optimizer that scales gradients by an exponential moving average of their squared values. "RMSProp \citep{tieleman2012rmsprop}"
- SANIA: A scale-invariant adaptive method that normalizes by squared gradients without square roots. "SANIA \citep{abdukhakimov2023sania}"
- Scale invariance: A property where optimization dynamics are unchanged under coordinate-wise rescaling of parameters. "scale invariance"
- Shampoo: A Kronecker-factored second-order optimizer using accumulated gradient covariances. "Shampoo \citep{gupta2018shampoo}"
- SignSGD: A first-order method that uses the sign of gradients, often linked to geometry. "SignSGD \citep{bernstein2018signsgd}"
- Singular value decomposition (SVD): Factorization of a matrix into singular vectors and values. "singular value decomposition "
- SOAP: A hybrid optimizer combining Shampoo’s Kronecker preconditioners with Adam-style diagonal adaptation in a preconditioned basis. "SOAP \citep{vyas2024soap}"
- Spectral geometry: Optimization geometry defined by the spectral norm and singular directions of matrices. "combine the spectral geometry of Muon with Adam-style preconditioning"
- Spectral norm: The largest singular value of a matrix; used to define spectral steepest descent updates. "the resulting operator norm coincides with the spectral norm"
- Steepest descent: A first-order optimization principle choosing the direction of maximal immediate loss decrease under a chosen norm. "The steepest descent principle provides one of the most classical formulations of first-order optimization"
- Surrogate Hessian: An approximate curvature matrix used in place of the true Hessian for preconditioning. "acts as a surrogate Hessian "
- SPlus: A hybrid optimizer combining Kronecker structure with a sign-based LMO. "SPlus \citep{frans2025stable}"
- Two sided preconditioning: Applying left and right matrix preconditioners around the gradient to form updates. "quasi-Newton updates are usually expressed through two sided preconditioning"
Collections
Sign up for free to add this paper to one or more collections.