MCMC: Bridging Rendering, Optimization and Generative AI (2510.09078v1)
Abstract: Generative AI has made unprecedented advances in vision LLMs over the past two years. During the generative process, new samples (images) are generated from an unknown high-dimensional distribution. Markov Chain Monte Carlo (MCMC) methods are particularly effective in drawing samples from such complex, high-dimensional distributions. This makes MCMC methods an integral component for models like EBMs, ensuring accurate sample generation. Gradient-based optimization is at the core of modern generative models. The update step during the optimization forms a Markov chain where the new update depends only on the current state. This allows exploration of the parameter space in a memoryless manner, thus combining the benefits of gradient-based optimization and MCMC sampling. MCMC methods have shown an equally important role in physically based rendering where complex light paths are otherwise quite challenging to sample from simple importance sampling techniques. A lot of research is dedicated towards bringing physical realism to samples (images) generated from diffusion-based generative models in a data-driven manner, however, a unified framework connecting these techniques is still missing. In this course, we take the first steps toward understanding each of these components and exploring how MCMC could potentially serve as a bridge, linking these closely related areas of research. Our course aims to provide necessary theoretical and practical tools to guide students, researchers and practitioners towards the common goal of generative physically based rendering. All Jupyter notebooks with demonstrations associated to this tutorial can be found on the project webpage: https://sinbag.github.io/mcmc/
Summary
- The paper presents a unified framework that integrates MCMC methods across physically based rendering, gradient-based optimization, and generative modeling.
- It details and contrasts algorithms like Metropolis-Hastings, Langevin, and Hamiltonian Monte Carlo, highlighting their trade-offs in high-dimensional sampling.
- The work demonstrates practical implications such as robust path sampling in rendering, scalable Bayesian inference, and stable generative model training.
MCMC: Bridging Rendering, Optimization, and Generative AI
This paper presents a comprehensive synthesis of Markov Chain Monte Carlo (MCMC) methods, elucidating their foundational role in physically based rendering, gradient-based optimization, and generative modeling. The authors systematically develop the theoretical underpinnings of MCMC, connect them to practical algorithms, and demonstrate their unifying power across disparate domains in computational science and AI.
Theoretical Foundations of MCMC
The exposition begins with a rigorous treatment of Markov chains and stochastic differential equations (SDEs), establishing the memoryless property and the construction of Markov processes for sampling from complex distributions. The paper details the discretization of SDEs via the Euler-Maruyama scheme, enabling practical simulation of stochastic processes such as Brownian motion and Langevin dynamics.
Figure 1: Overview of MCMC methods for sampling from complex distributions, with applications in rendering and generative modeling.
The authors emphasize the importance of gradient information in efficient exploration of high-dimensional spaces. Langevin dynamics leverages the gradient of the log-probability, while Hamiltonian dynamics introduces auxiliary momentum variables and exploits phase space geometry for coherent exploration. The leapfrog symplectic integrator is highlighted as a robust numerical method for simulating Hamiltonian trajectories, ensuring volume preservation and efficient mixing.
Figure 2: Gradient-based exploration and Hamiltonian dynamics enable efficient sampling in high-dimensional parameter spaces.
MCMC Algorithms: Metropolis-Hastings, Langevin, and Hamiltonian Monte Carlo
The paper provides detailed algorithmic descriptions and code-level pseudocode for Metropolis-Hastings (MH), Langevin Monte Carlo (LMC), Annealed Langevin Monte Carlo (ALMC), and Hamiltonian Monte Carlo (HMC). The trade-offs between these methods are systematically analyzed:
- MH: General applicability, but poor mixing in high dimensions and strong dependence on proposal distribution.
- LMC: Gradient-informed proposals improve efficiency, but require smoothness and careful discretization.
- HMC: Superior performance in high-dimensional, smooth distributions, but computationally intensive and sensitive to hyperparameters.
The authors present a comparative analysis of autocorrelation, scalability, convergence, and suitability for multimodal distributions, providing clear guidance for method selection in practical scenarios.
MCMC in Physically Based Rendering
The path space formulation of light transport is presented as a high-dimensional integration problem, where MCMC methods are essential for robust sampling. The paper reviews multiple importance sampling (MIS) and its balance heuristic, demonstrating variance reduction in Monte Carlo estimators.
The limitations of sequential path sampling are illustrated in challenging scenarios such as caustic rendering, where specular-diffuse-specular (SDS) paths are difficult to sample efficiently. MCMC-based methods, notably Metropolis Light Transport (MLT), are shown to amortize the cost of discovering rare but important paths by exploring their neighborhoods.
Figure 3: MLT mutation rules enable systematic exploration of path space, improving convergence in difficult rendering scenarios.
Primary Sample Space MLT (PSSMLT) is introduced as a practical alternative, operating in the space of random numbers and leveraging black-box mappings for integration. The Hessian-Hamiltonian MLT variant further improves local exploration by modeling anisotropic dependencies via the Hessian of the integrand.
Figure 4: PSSMLT performs mutations in primary sample space, simplifying implementation and leveraging existing importance sampling techniques.
MCMC in Optimization
The paper draws a formal connection between stochastic gradient descent (SGD) and MCMC, showing that SGD updates form a Markov chain. Stochastic Gradient Langevin Dynamics (SGLD) augments SGD with noise, enabling sampling from the posterior in Bayesian inference.
The authors provide explicit update rules and code snippets for SGLD, highlighting its utility in large-scale Bayesian learning where exact MCMC is infeasible. The distinction between point estimation (MAP) and posterior sampling is clarified, and the role of noise in escaping local minima and exploring parameter space is emphasized.
MCMC in Generative Modeling
The generative modeling section traces the evolution from variational autoencoders (VAEs) to hierarchical VAEs (HVAEs) and variational diffusion models (VDMs). The evidence lower bound (ELBO) is derived as a tractable surrogate for likelihood maximization, and its decomposition into reconstruction and prior matching terms is detailed.
Figure 5: Markovian hierarchical VAE model with multiple latent steps, enabling expressive generative modeling.
VDMs are presented as Markovian HVAEs with fixed Gaussian encoders, where the latent dimension matches the data dimension and the encoder parameters are predefined. The sampling procedure is reduced to iterative denoising transitions, connecting directly to the theoretical framework of MCMC.
Figure 6: Variational diffusion model adds linear Gaussian noise at each time step, culminating in a standard Gaussian at the final latent step.
Energy-based models (EBMs) are discussed as flexible, unnormalized models where MCMC is essential for both training (via contrastive divergence) and sampling. The paper provides explicit gradient derivations for likelihood maximization and discusses the computational challenges of sampling in high dimensions.
Score-based generative models are introduced as an alternative, where the score function (gradient of log-probability) is learned directly, and sampling is performed via Langevin dynamics. This approach circumvents the need for normalization constants and enables efficient sample generation.
Practical and Theoretical Implications
The unification of MCMC methods across rendering, optimization, and generative modeling has significant implications:
- Rendering: MCMC enables robust sampling in high-dimensional path spaces, improving convergence and realism in physically based rendering.
- Optimization: MCMC-inspired algorithms such as SGLD provide scalable Bayesian inference, bridging the gap between deterministic optimization and probabilistic modeling.
- Generative AI: Diffusion models and score-based generative models leverage MCMC principles for stable training and high-fidelity sample generation.
The paper identifies key challenges, including the invariance and reversibility constraints of MH, slow mixing, and excessive local exploration. Recent advances in continuous-time Markov frameworks and rejection-free algorithms are highlighted as promising directions for overcoming these limitations.
Conclusion
This work establishes MCMC as a foundational bridge linking physically based rendering, gradient-based optimization, and generative modeling. The theoretical rigor and practical algorithms presented provide a unified framework for sampling from complex distributions, with direct applications in graphics, machine learning, and AI. The synthesis of these domains opens avenues for future research in scalable, robust, and physically realistic generative models, and underscores the centrality of probabilistic reasoning in computational science.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is a set of course notes that teach how a family of methods called Markov Chain Monte Carlo (MCMC) can connect three big areas in computing:
- Physically based rendering (making realistic images by simulating light),
- Optimization (the math used to train machine learning models),
- Generative AI (models that create images, text, etc., especially diffusion models).
The main idea is that many problems in these areas involve dealing with complex randomness. MCMC gives us smart ways to explore and sample from complicated “distributions” (the shapes of possible outcomes), which helps us render images more realistically, train AI more efficiently, and generate better samples.
Objectives and Questions
The course aims to answer a few simple questions:
- How can we sample from very complicated, high-dimensional probability distributions when simple methods fail?
- Why do MCMC methods help both in making realistic graphics (rendering) and in training and running generative AI models?
- How do ideas like random motion (Brownian motion), guided motion (Langevin dynamics), and energy/momentum (Hamiltonian dynamics) improve sampling?
- In what way is common optimization (like Stochastic Gradient Descent, or SGD) itself a kind of Markov chain?
- How can we move toward “generative physically based rendering,” where AI-generated images obey real physics?
Methods and Approach (Explained Simply)
The course builds up concepts step-by-step, starting from basic probability and moving toward practical algorithms and applications.
- Markov chains: Imagine walking through a maze where each step depends only on where you are now, not on how you got there. That “memoryless” walk is a Markov chain.
- Stochastic differential equations (SDEs): These describe motion with randomness over time. Think of a pollen grain jiggling around in water. Even though each jiggle is random, overall behavior can be predicted statistically.
- Brownian motion: Pure random wandering, like a drunkard’s walk.
- Langevin dynamics: Random wandering plus a “push” in a helpful direction (using gradients). Like drifting toward a low valley while still being jostled by noise.
- Hamiltonian dynamics: Motion with position and momentum, like a satellite orbiting a planet. Momentum keeps you moving efficiently through space without getting stuck.
- Monte Carlo integration: When you can’t solve a big complicated math problem exactly, you try many random samples and average them. This is how many renderers estimate light.
- MCMC sampling: Instead of taking random samples anywhere, you build a smart walk (a Markov chain) that spends more time in important areas. Common methods include:
- Metropolis–Hastings: Propose a move, accept it based on how good it is; simple but can be slow.
- Langevin Monte Carlo: Uses gradients to propose better moves, so it explores more intelligently.
- Hamiltonian Monte Carlo: Uses momentum to make long, efficient moves, great in high dimensions.
- Rendering applications:
- Path space: Light moves along paths from sources to the camera. Integrals over many possible paths determine pixel brightness.
- Multiple Importance Sampling (MIS): When you have several ways to sample light paths, mix them wisely to reduce noise.
- Metropolis Light Transport (MLT): An MCMC method that explores neighboring light paths to handle tricky scenes (like sharp reflections, glass, and caustics—the bright patterns at the bottom of a pool).
- Primary Sample Space MLT (PSSMLT): A simpler twist on MLT that works by nudging the random inputs of an existing renderer, making implementation easier.
- Optimization and generative models:
- SGD as a Markov chain: Each update depends only on the current parameters and a fresh random batch—so training steps form a chain.
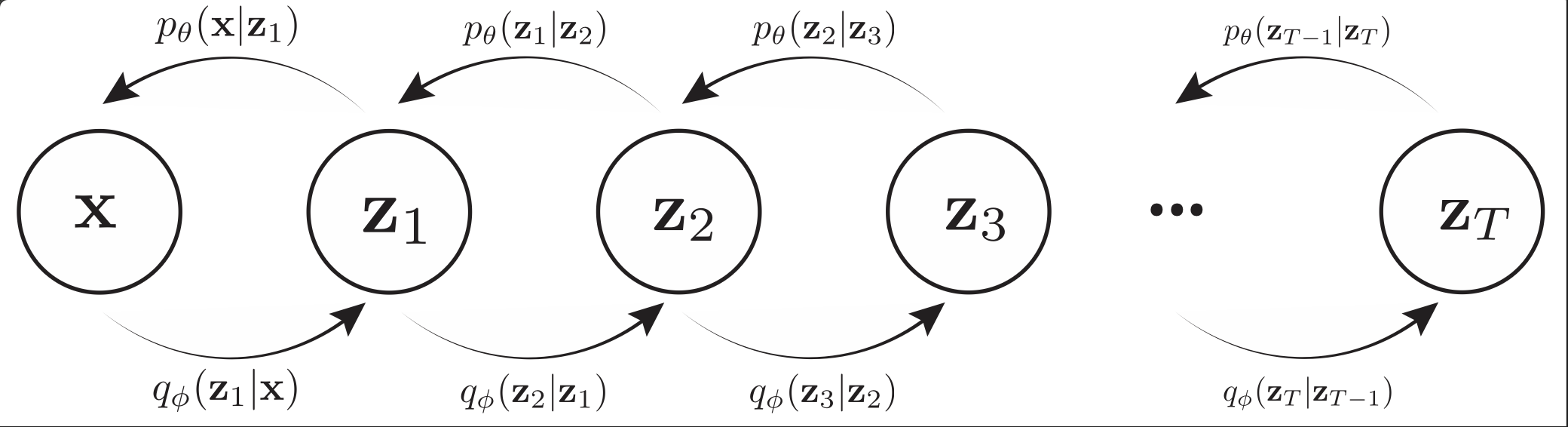
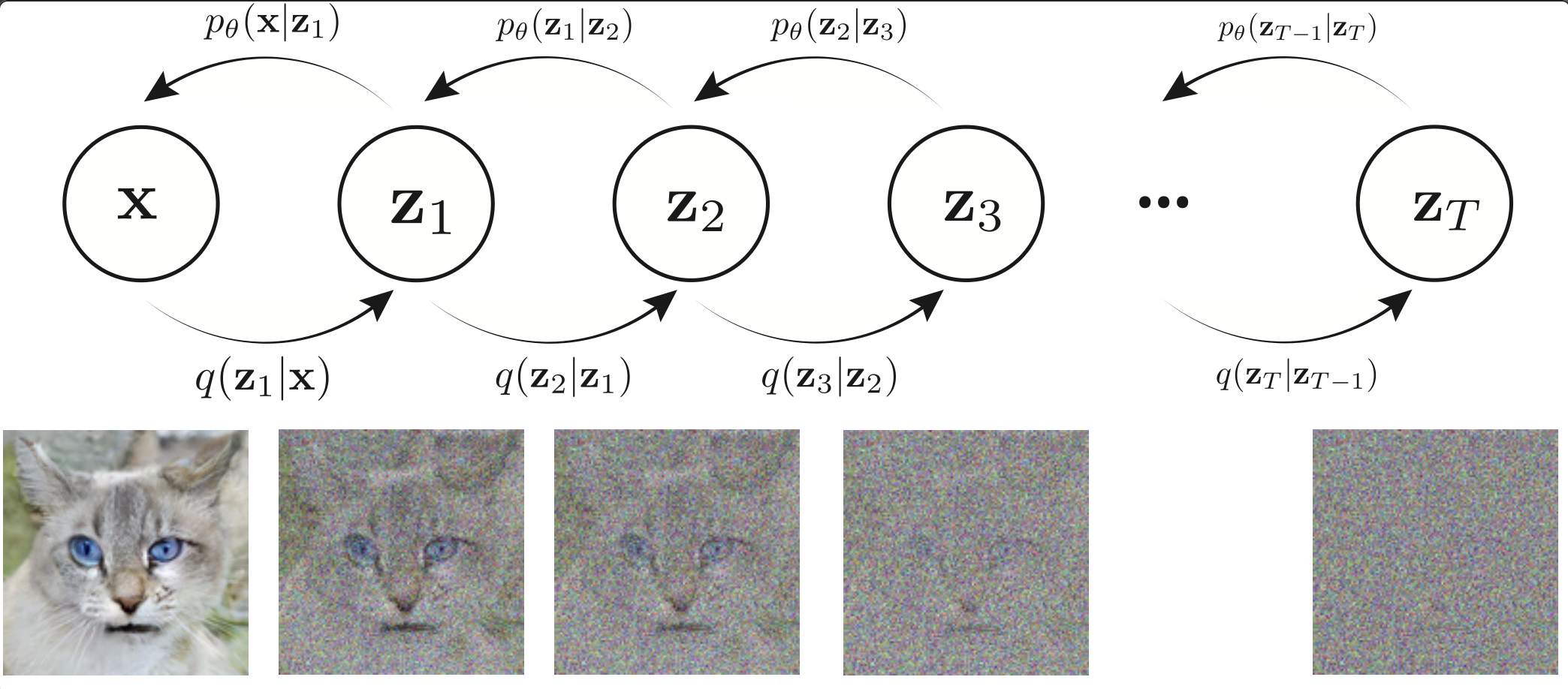
- Diffusion models and SDEs: These modern generative models can be viewed through the lens of SDEs, connecting them naturally to MCMC ideas.
- Variational Autoencoders (VAEs), energy-based models: Other generative approaches that benefit from sampling and optimization insights.
Main Findings and Why They Matter
Instead of presenting new experiments, the course pulls together theory and practice across fields and highlights key takeaways:
- MCMC is a common thread: The same sampling ideas power realistic rendering, optimization, and modern generative AI.
- Gradients help: Using gradient information (how to move “downhill” toward better regions) makes sampling and training much more efficient.
- Momentum matters: Hamiltonian methods with momentum can explore tough, high-dimensional spaces without getting stuck.
- Rendering gets robust: MLT and PSSMLT can handle difficult light paths (like in scenes with glass or caustics) better than standard random sampling.
- AI gets principled: Viewing diffusion models and other generative approaches through SDEs and MCMC gives a solid mathematical foundation for training and sampling.
Implications and Impact
- Better, more realistic visuals: MCMC-based rendering techniques reduce noise and handle complex lighting, making images look more physically correct.
- Smarter AI generation: Tying diffusion models to SDEs and MCMC improves our understanding of how to train and sample, potentially leading to faster or more accurate generative models.
- Unified thinking: Seeing optimization, rendering, and generation under one framework encourages cross-pollination—ideas from one area can improve the others.
- Practical tools: The course provides theory and hands-on notebooks to help students and researchers apply these methods. This supports future work toward “generative physically based rendering,” where AI-generated images respect real-world physics.
In short, the course shows how MCMC can be the bridge between making images the right way (physics), training models the smart way (optimization), and generating content the creative way (AI).
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what the paper leaves missing, uncertain, or unexplored, aimed at guiding future research:
- Unified framework: No rigorous probabilistic formulation that jointly covers rendering path-space sampling, gradient-based optimization (SGD as Markov chain), and diffusion/score-based generative modeling under one MCMC framework (state spaces, objectives, correctness guarantees).
- Convergence guarantees in rendering: Missing proofs or formal conditions (irreducibility, aperiodicity, detailed balance) that ensure MLT/PSSMLT chains converge in realistic scenes, especially with specular–diffuse–specular (SDS) paths and delta interactions.
- Convergence diagnostics: No methodology for practical diagnostics in MCMC rendering (e.g., effective sample size per pixel, Gelman–Rubin R̂, autocorrelation analysis), burn-in length selection, or stopping criteria.
- Quantitative comparisons: Absent empirical benchmarks comparing MH, LMC/MALA, and HMC for path-space sampling (acceptance rates, variance reduction, noise vs. sample count, wall-clock time) on canonical scenes (caustics, glossy materials, and volumes).
- SDE correctness and reproducibility: Key SDE and discretization equations are underspecified/inconsistent (drift/diffusion terms, time-step effects), preventing reproducible implementations; need corrected formulations and stability/error analyses.
- Discretization bias: Unaddressed bias from discretized Langevin updates in rendering; conditions and practical recipes for Metropolis adjustment (MALA) to restore the correct stationary distribution.
- Gradients in path space: How to obtain or approximate ∇ log p in path-space where visibility and delta BSDF terms produce non-differentiabilities; evaluation of differentiable rendering, soft visibility, reparameterizations, or surrogate scores.
- HMC for rendering: Feasibility and design of HMC in path-space (mass matrix choice, momentum distribution), robustness of symplectic integrators under discontinuities, and applicability of NUTS or Riemannian HMC.
- Multimodality handling: Strategies to traverse disparate path families/modes (tempered transitions, parallel tempering, annealing schedules tailored to SDS/glossy cases), including tuning guidelines and correctness.
- MIS–MCMC integration: Principled ways to incorporate MIS (including negative weights) within MCMC acceptance ratios, co-sampling multiple proposals in a single chain, and proofs of variance/correctness improvements.
- Hyperparameter tuning: Automatic, scene-aware tuning of step sizes, leapfrog steps, temperature schedules, and preconditioners for rendering workloads (e.g., adaptive algorithms or learned samplers).
- Scalability and systems: GPU/accelerator-friendly implementations of MLT/PSSMLT and Langevin/HMC, parallel chain orchestration across pixels, memory layout, and reproducibility across hardware/software stacks.
- Singularities and delta terms: Robust mutation kernels and acceptance computations near specular constraints and measure-zero sets; correctness proofs and practical heuristics to avoid chain stickiness/bias.
- Normalization in histogram-based rendering: Efficient, unbiased estimation of the global scale factor for image reconstruction from marginal histograms, with variance analysis and practical estimators.
- Chain initialization: Strategies to find initial SDS/caustic paths cheaply (e.g., warm starting from path tracing, learned proposals), reuse across pixels, and effects on burn-in and mixing.
- PSSMLT details: Proposal design in primary sample space (u-space), acceptance behavior under variable path length, controlling correlations introduced by warps, and empirical guidance on mutation kernels.
- Beyond surfaces: Extension of the framework to volumetric media, participating scattering, spectral effects, and motion blur; impact on mutation rules, gradients, and convergence.
- Temporal coherence: MCMC sampling for dynamic scenes/video, chain reuse across frames, maintaining temporal coherence while preserving correctness.
- Typical set geometry: Formalization of “typical set” for rendering path-space (measure concentration, geometry) and its implications for sampler design and diagnostics.
- Optimization bridge: Concrete algorithms that leverage Langevin/HMC to explore inverse rendering/material estimation loss landscapes; trade-offs vs. SGD, computational budgets, and stopping/adaptation strategies.
- Generative AI integration: Explicit mechanisms to inject physical constraints (rendering equation residuals, energy terms) into diffusion/score models; using learned scores to propose path mutations; training/validation pipelines.
- Energy-based models for rendering: Specification of energies tied to path contributions, visibility, and constraints; training regimes, sampler choices, preconditioning, and comparison against diffusion/VAE baselines.
- Evaluation protocol: Standardized scene suites, metrics (variance, ESS, PSNR/SSIM, perceptual measures), ablations of mutation sets, and reproducible code; the notes reference notebooks but provide no systematic empirical results.
- Failure modes and safety: Identification and mitigation of non-ergodicity, chain stickiness near constraints, rejection-induced bias, and remedies (reparameterization, resampling, reflective boundaries, adaptive proposals).
Practical Applications
Immediate Applications
Below is a concise set of actionable use cases that can be deployed with current methods and tooling derived from the paper’s findings and techniques.
- Production-grade caustics and SDS effects via MLT/PSSMLT — sectors: media/entertainment, design/architecture, automotive visualization
- Tools/products/workflows: Integrator plug-ins for existing renderers (e.g., Mitsuba, PBRT, Arnold, RenderMan) that switch to Metropolis Light Transport (MLT) or Primary Sample Space MLT (PSSMLT) when variance diagnostics detect specular–diffuse–specular (SDS) paths; render-farm job profiles that enable MCMC-based integrators for caustic-heavy shots.
- Assumptions/dependencies: Accurate BSDFs and visibility; correct MIS weighting; careful mutation design; tuning of acceptance rates and burn-in; scene complexity may impact convergence.
- Faster convergence previews for challenging scenes — sectors: CAD, product design, AR/VR
- Tools/products/workflows: Progressive PSSMLT-based “difficult-lighting mode” for interactive look-dev; designer-facing toggles to bias toward lens/caustic perturbations described in the course notes.
- Assumptions/dependencies: GPU-friendly implementations, stable perturbation kernels; performance depends on scene structure and noise thresholds acceptable for previews.
- Variance-aware denoising and confidence maps — sectors: VFX, visualization, medical/engineering simulation
- Tools/products/workflows: Per-pixel effective sample size (ESS) and posterior variance estimates from MCMC chains to drive denoisers and QA; auto-flagging of under-sampled regions (e.g., caustics through glass).
- Assumptions/dependencies: Additional samples/chains to estimate uncertainty; calibration of confidence-to-noise mappings; denoiser integration.
- Robust optimization via SGLD/MALA noise in training loops — sectors: AI/ML software
- Tools/products/workflows: Stochastic Gradient Langevin Dynamics (SGLD) or Metropolis-adjusted Langevin (MALA) options in modern training frameworks (PyTorch/TF) to improve exploration, generalization, and escape sharp minima; annealing schedules (ALMC-inspired) for curriculum training.
- Assumptions/dependencies: Access to gradients; step-size/noise scheduling; modest compute overhead; benefits depend on model smoothness and loss landscape.
- Practical posterior sampling for energy-based and diffusion models — sectors: generative AI
- Tools/products/workflows: LMC/ALMC samplers for EBMs; post-hoc Langevin refinement of diffusion latents; temperature schedules to navigate multimodality before concentrating on high-probability regions.
- Assumptions/dependencies: Computation of ∇log p(x) (score or energy gradients); annealing schedule design; compute budgets for extra sampling steps.
- Renderer diagnostics for “insufficient techniques” — sectors: rendering software, tools
- Tools/products/workflows: Built-in diagnostics that use MCMC mutations (lens/caustic/multi-chain perturbations) to identify path classes causing high variance; dashboard-style reports recommending integrator changes or light-path expression hints.
- Assumptions/dependencies: Access to sampler hooks and path logs; reproducible proposal densities; overhead acceptable in debug builds.
- Courseware and curricula using the provided Jupyter notebooks — sectors: academia, professional training
- Tools/products/workflows: Cross-disciplinary courses (graphics + ML) using the project notebooks (SDEs, Langevin/HMC, MLT/PSSMLT); research lab tutorials to bootstrap Bayesian inference and rendering literacy.
- Assumptions/dependencies: Python environments, GPU where needed; open-source renderers (e.g., Mitsuba) for hands-on labs.
- Energy-aware render-farm policies — sectors: studio operations, sustainability/policy in production pipelines
- Tools/products/workflows: Shot classification that routes difficult lighting to MLT/PSSMLT to reduce re-render/iteration cycles; KPIs tied to variance targets and kWh/frame.
- Assumptions/dependencies: Metered energy use; pipeline buy-in; integrator selection automation; QA thresholds to prevent over-sampling.
- Bayesian inference templates for domain science — sectors: healthcare, finance, energy systems
- Tools/products/workflows: HMC/LMC recipes for posterior inference in high-dimensional models (e.g., parameter estimation, risk models), leveraging concepts and code patterns from the course.
- Assumptions/dependencies: Differentiable log posteriors; good priors; tuning of step size/leapfrog steps; convergence diagnostics (R̂, ESS).
Long-Term Applications
These use cases require further research, scaling, integration, or hardware/software advances before becoming broadly deployable.
- Unified “generative physically based rendering” (GPBR) — sectors: media/entertainment, e-commerce, robotics simulation
- Tools/products/workflows: Diffusion/EBM models constrained by light transport (via SDE/MCMC priors) to generate physically consistent images and materials; text-to-3D pipelines with physically faithful caustics and refractions; MCMC-guided inverse rendering.
- Assumptions/dependencies: Differentiable renderers at scale; large paired datasets (geometry/material/illumination); efficient score/energy training; hybrid MIS–MCMC learning.
- Real-time or near-real-time MCMC rendering on GPUs — sectors: gaming, AR/VR, design collaboration
- Tools/products/workflows: GPU-optimized PSSMLT/MLT kernels and symplectic integrators for real-time path mutation; adaptive kernels that maintain high acceptance at low latency.
- Assumptions/dependencies: Hardware acceleration for correlated sampling; low-overhead random number and mutation pipelines; stability under scene dynamics.
- Learned proposal distributions for MLT — sectors: rendering software, media tech
- Tools/products/workflows: Neural proposal networks trained to predict effective perturbations (lens/caustic/multi-chain) and local path neighborhoods; MIS with learned, scene-adaptive proposals.
- Assumptions/dependencies: Generalization across materials/lighting; safety under rare path classes; variance guarantees with learned proposals.
- Physically based sensor simulation for autonomy — sectors: robotics, automotive
- Tools/products/workflows: MCMC-enhanced simulators that reproduce glare, multiple scattering, and rare optical edge cases for cameras/LiDAR; curriculum training with annealed samplers for rare-event data generation.
- Assumptions/dependencies: Integration with simulators (e.g., CARLA, Isaac); performance scaling; accurate sensor/scene models and validation.
- Biomedical optics and therapy planning — sectors: healthcare/biomedical engineering
- Tools/products/workflows: MLT-based path sampling for light transport in tissue to improve optical tomography, endoscopy simulation, and phototherapy dose planning under complex scattering.
- Assumptions/dependencies: Validated tissue optical models; computational acceleration; regulatory pathways for clinical decision support.
- City-scale daylighting and energy codes — sectors: energy, urban planning, policy
- Tools/products/workflows: MCMC-rendered daylight/reflection analyses in dense urban scenes to inform building codes and façade/glazing standards; uncertainty-aware reports for policy decisions.
- Assumptions/dependencies: Accurate GIS/geometry/material databases; scalable compute; alignment with policy processes and standards bodies.
- HMC-inspired optimizers for deep learning at scale — sectors: AI/ML platforms
- Tools/products/workflows: Hybrid deterministic–stochastic optimizers that maintain exploration (momentum + noise) in non-convex landscapes; plug-in PyTorch/TF optimizers for foundation models.
- Assumptions/dependencies: Theoretical and empirical stability at trillion-parameter scales; efficient gradient/momentum management; scheduler design.
- Uncertainty-quantified generative AI — sectors: healthcare, finance, safety-critical AI, policy
- Tools/products/workflows: MCMC-based uncertainty bands around diffusion outputs (images, 3D, time series) for downstream risk assessments and auditing; policy frameworks requiring uncertainty disclosure for automated content.
- Assumptions/dependencies: Access to model scores/energies; calibration datasets; standardized uncertainty reporting.
- Automated integrator selection and scene rewrites — sectors: DCC tools, rendering pipelines
- Tools/products/workflows: Scene analyzers that predict when MIS will fail and recommend MLT/PSSMLT or material/light-path adjustments; auto-rewrites of shaders/light-path expressions to reduce singularities.
- Assumptions/dependencies: Reliable predictors; integration with DCC (e.g., Blender, Houdini); artist oversight; robustness to creative intent.
Glossary
- Acceptance ratio: The probability of accepting a proposed move in Metropolis-Hastings, ensuring detailed balance. "Compute the acceptance ratio and accept or reject the proposed state based on a random draw from a uniform distribution."
- Annealed Langevin Monte Carlo (ALMC): A Langevin Monte Carlo variant that uses a decreasing temperature schedule to better explore multimodal distributions. "Annealed Langevin Monte Carlo (ALMC) is a variant of LMC that introduces an annealing schedule."
- Autocorrelation: Correlation between successive samples in a chain; high values indicate poor mixing and less efficient sampling. "slow mixing and high autocorrelation"
- Balance heuristic: A multiple importance sampling weighting rule that balances contributions by their sampling densities. "A particularly simple weighting function known as the balance heuristic has the following expression for two input strategies:"
- Bidirectional mutation: An MLT path-space mutation that replaces a segment of the current path with a newly generated segment. "Bidirectional mutation:"
- Bidirectional path tracing: A rendering technique that builds paths from both the camera and the light and connects them. "using the building blocks of bidirectional path tracing to sample paths."
- Bidirectional sampling methods: Strategies that sample from lights and camera and attempt to connect subpaths. "Bidirectional sampling methods (Figure~\ref{fig:unbiased-difficulties}~(c)) tracing from both sides also fail:"
- Bidirectional scattering distribution function (BSDF): A function describing how light scatters at a surface from one direction to another. "$f(x_{k-1}\tox_k\tox_{k+1})$ is the \emph{bidirectional scattering distribution function} (BSDF), which specifies how"
- Boltzmann distribution: Probability distribution relating state probability to energy, central to connecting potentials to target densities. "The key relationship between potential energy and the probability distribution is given by the Boltzmann distribution in thermal equilibrium ."
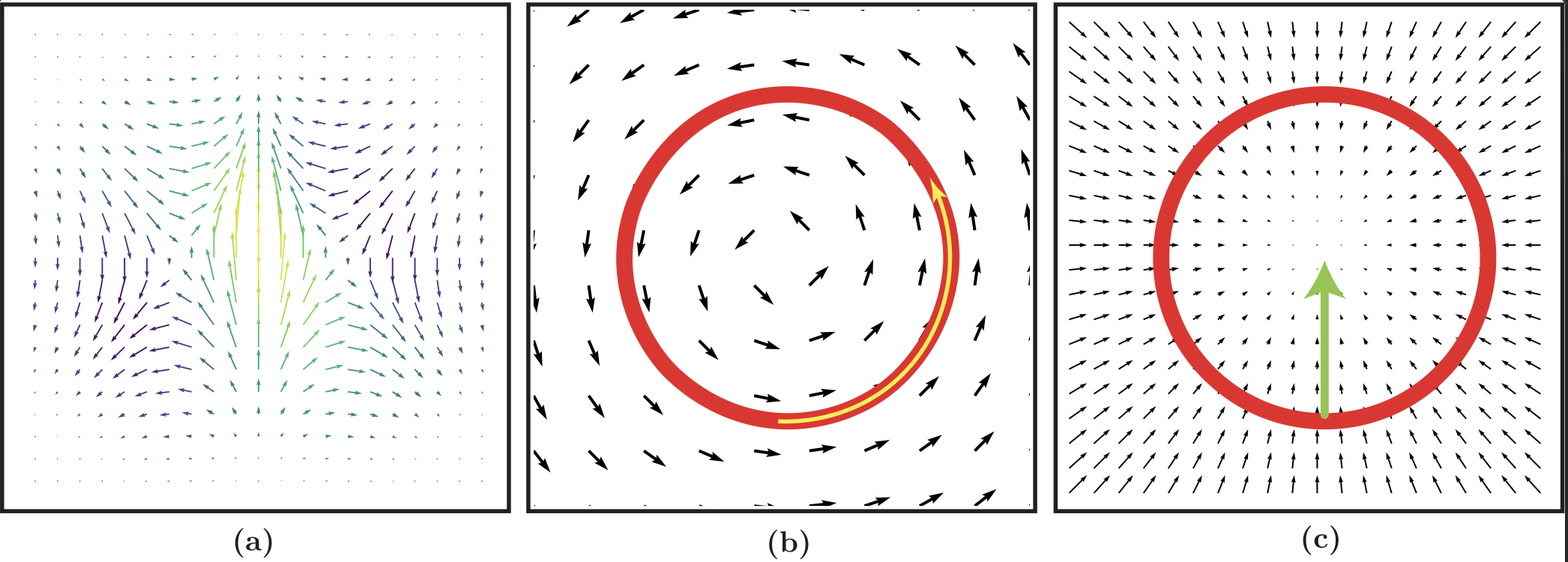
- Brownian motion: A continuous-time stochastic process with independent Gaussian increments; the canonical model of random motion. "Brownian motion is the simplest form of an SDE and serves as the foundation for more complex models (like Langevin dynamics)."
- Burn-in period: Initial iterations of an MCMC chain discarded to allow convergence to the stationary distribution. "Collect samples after a burn-in period (initial samples are discarded to allow the chain to converge)."
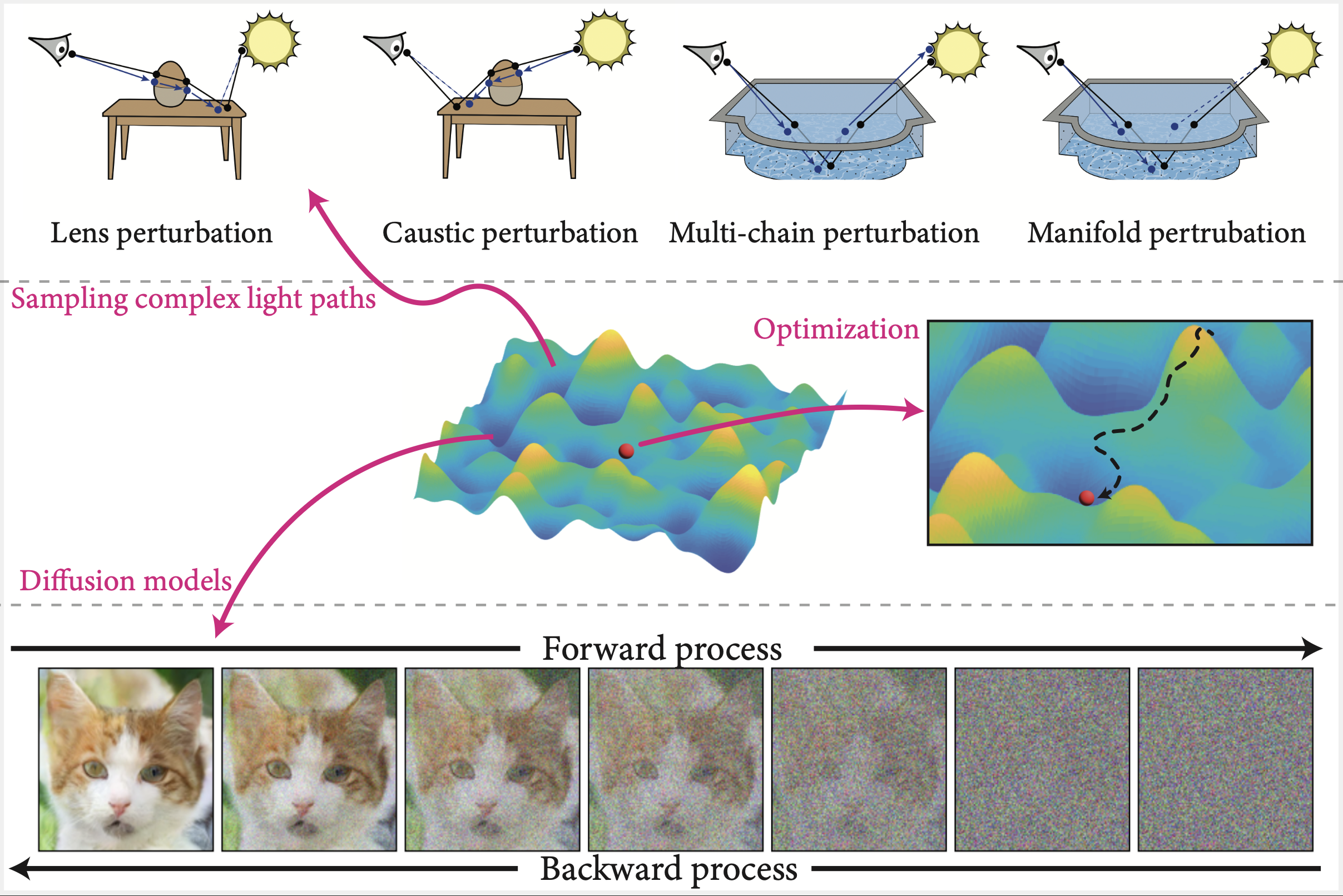
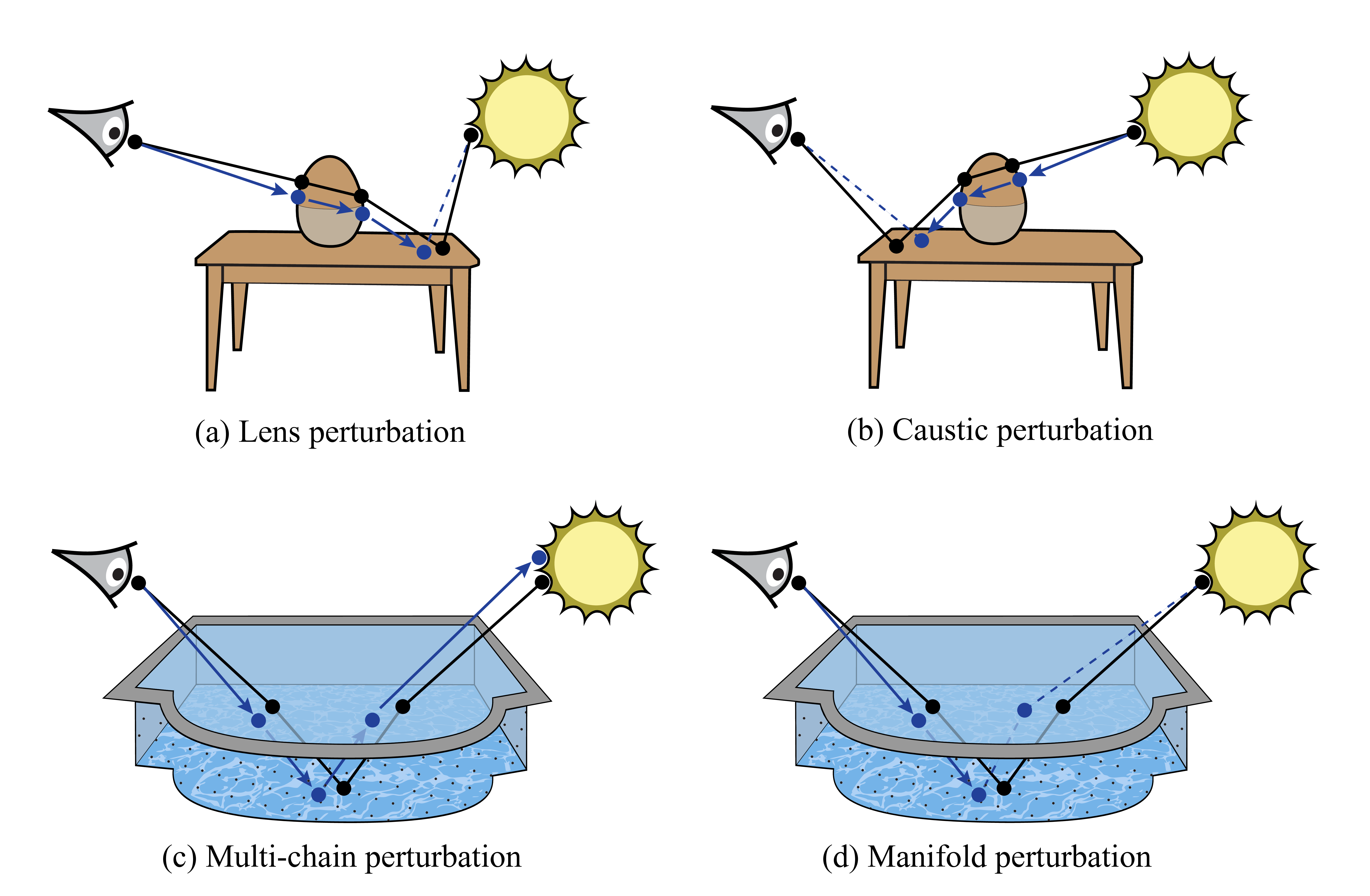
- Caustic perturbation: An MLT perturbation designed to handle caustics by tracing from the light side. "The caustic perturbation (Figure~\ref{fig:mlt-perturbations}b) works just like the lens perturbation, except that it proceeds in reverse starting at the light source."
- Caustics: Concentrated light patterns formed by reflection/refraction, challenging for many sampling methods. "when rendering caustic patterns at the bottom of a swimming pool."
- Conservative dynamics: Dynamics that preserve volumes (and often energy) in phase space, crucial for HMC correctness. "Conservative dynamics in physical systems requires that volumes are exactly preserved."
- Diffusion-based generative models: Generative models trained via denoising/diffusion processes with stable training dynamics. "These advances are largely due to diffusion-based generative models, which are very stable and simple to train."
- Energy-based models: Probabilistic models defined via an unnormalized energy function instead of explicit likelihoods. "We then discuss energy-based models which, although slow to train, provides a lot of flexibility."
- Ergodicity: Property ensuring a Markov chain can explore the entire state space and converge to a unique stationary distribution. "This rule generally has a low acceptance ratio but it is essential to guarantee ergodicity of the resulting Markov Chain."
- Euler-Maruyama method: A numerical scheme for discretizing and simulating stochastic differential equations. "The Euler-Maruyama method is a numerical scheme used to approximate the solution of stochastic differential equations (SDEs)."
- Evidence lower bound (ELBO): A variational objective used to train latent-variable models like VAEs. "we study variational autoencoders, how they are driven by evidence lower bound"
- Fokker-Planck equation: A PDE that governs the time evolution of probability densities for diffusion processes. "it's often modeled using the Fokker-Planck equation for probability density evolution"
- Geometric term: The term in path-space integrals accounting for visibility and geometric coupling along segments. "$G(x\leftrightarrowy)$ is the geometric term, which"
- Hamilton's equations: Coupled ODEs describing the time evolution of position and momentum in Hamiltonian mechanics. "The dynamics of the system are governed by two main equations, known as Hamilton's equations, which tell us how the position and momentum change over time."
- Hamiltonian dynamics: Physics-based dynamics over position and momentum that preserve volume; leveraged by HMC for efficient exploration. "In Hamiltonian dynamics, we describe a system using a function called the Hamiltonian, which usually represents the total energy (kinetic + potential) of the system."
- Hamiltonian function: The total energy function (potential plus kinetic) defining Hamiltonian dynamics. "The Hamiltonian function represents the total energy of the system and is typically given by:"
- Hamiltonian Monte Carlo (HMC): An MCMC method that uses Hamiltonian dynamics to propose distant, low-reject moves in high dimensions. "A direct connection between SDEs and MCMC is also found in the Hamiltonian Monte Carlo (HMC) method."
- Importance sampling: Monte Carlo technique that draws samples from a proposal and reweights to estimate integrals efficiently. "Importance sampling is one such strategy and is known to reduce the variance."
- Inverse transform method: Procedure to sample from a target distribution by inverting its CDF on uniform random inputs. "In practice, the inverse transform method is almost always used to realize this warping step."
- Langevin dynamics: An SDE combining deterministic drift from the log-density gradient with stochastic noise to explore distributions. "Langevin dynamics describes the motion of a particle under the influence of both deterministic forces and random noise."
- Langevin Monte Carlo (LMC): An MCMC algorithm that discretizes Langevin dynamics to sample from target distributions. "Langevin Monte Carlo (LMC) is a class of Markov Chain Monte Carlo (MCMC) algorithms that generate samples from a probability distribution of interest by simulating the Langevin Equation."
- Leapfrog integrator: A symplectic integrator used in HMC that alternates momentum and position updates and preserves volume. "then we can employ a simple leapfrog integrator."
- Lens perturbation: An MLT perturbation that slightly adjusts the camera subpath while keeping the rest of the path fixed. "Lens perturbation: This transition rule shown in Figure~\ref{fig:mlt-perturbations}a only perturbs the lens subpath rather than regenerating it from scratch."
- Lens subpath mutation: An MLT mutation that regenerates only the camera-connected portion of the path. "Lens subpath mutation: The lens subpath mutation is similar to the previous mutation but only replaces the lens subpath,"
- Markov chain: A stochastic process with memoryless transitions where the next state depends only on the current state. "Markov Chains are mathematical models used to describe systems that transition from one state to another, where the probability of each transition depends only on the current state"
- Markov Chain Monte Carlo (MCMC): A family of algorithms that construct Markov chains whose stationary distribution is the target, enabling sampling/integration. "MCMC methods are powerful tools for sampling from complex, high-dimensional probability distributions"
- Metropolis-Hastings algorithm: A foundational MCMC algorithm that proposes moves and accepts them with a probability ensuring the correct stationary distribution. "The Metropolis-Hastings algorithm is an MCMC method for obtaining a sequence of samples from a probability distribution from which direct sampling is difficult."
- Metropolis Light Transport (MLT): An MCMC-based rendering algorithm that explores path space via specialized mutations and perturbations. "In 1997, Veach and Guibas proposed an unusual rendering technique named Metropolis Light Transport \citep{veach1997metropolis},"
- Multiple importance sampling (MIS): A strategy to combine multiple estimators using weights based on their sampling densities to reduce variance. "This is the key insight of a widely used technique known as multiple importance sampling (MIS)~\citep{Veach:1995:OCS}."
- Path space: The space of all light transport paths; an integral formulation over paths for rendering. "path space formulation"
- Path tracing: A Monte Carlo rendering algorithm that samples light paths from the camera using random walks. "Path tracing in Figure~\ref{fig:unbiased-difficulties}~(b) generates paths from the opposite end and also remains extremely inefficient."
- Phase space: The combined position-momentum space in which Hamiltonian dynamics evolve. "the state of a Hamiltonian system is represented in a space called phase space,"
- Physically based rendering: Rendering that simulates light transport and material interactions via physically grounded models. "MCMC methods have shown an equally important role in physically based rendering"
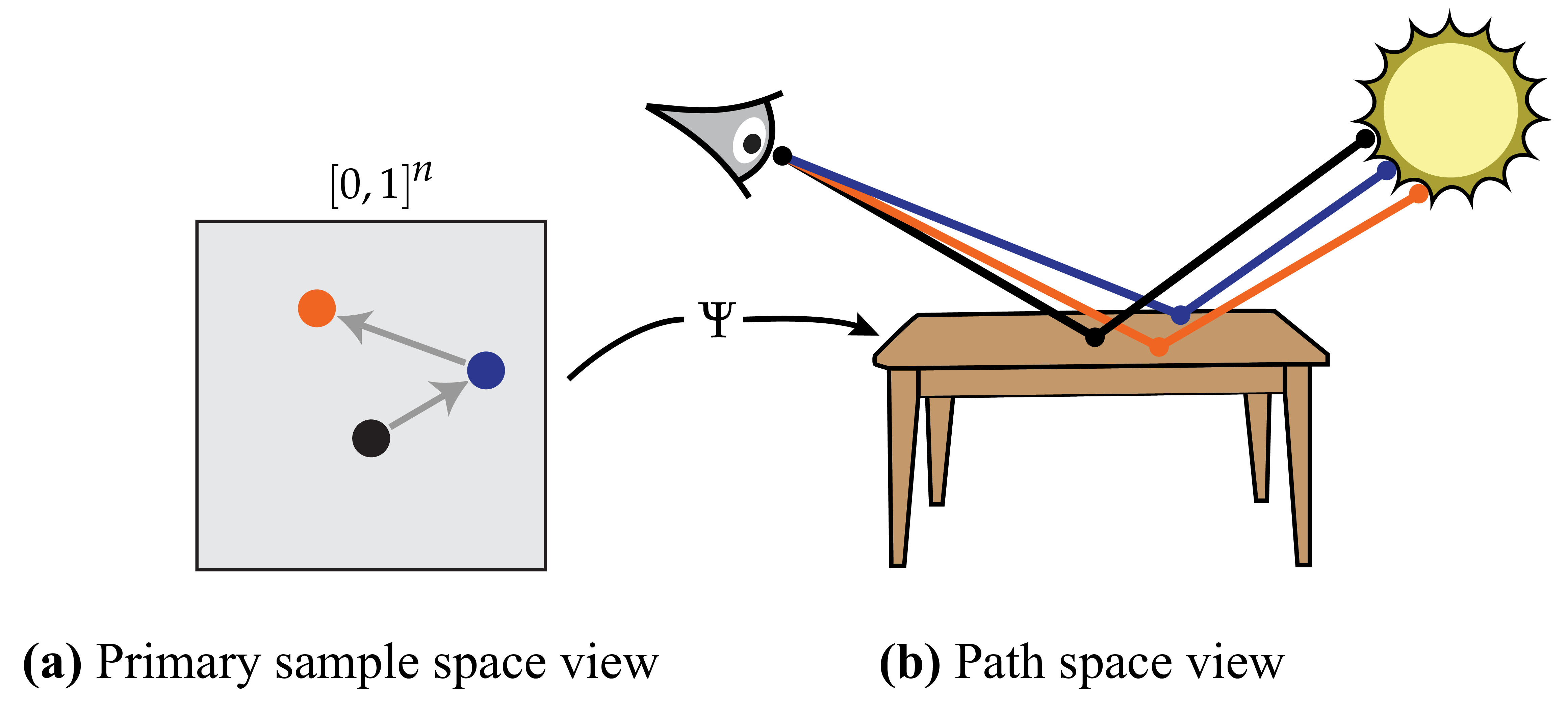
- Primary Sample Space MLT (PSSMLT): An MLT variant that operates on the unit hypercube of random numbers feeding the sampler instead of path space. "The main idea underlying their method named \emph{Primary Sample Space MLT} (PSSMLT) is general and can also be applied to integration problems outside of rendering."
- Proposal distribution: The distribution from which candidate states are drawn in MH or importance sampling. "This strategy can be quite efficient if proposal distribution is well-matched with the target distribution."
- Random walk: A process of successive random steps, often used to describe or simulate Brownian motion and baseline MCMC moves. "Simulating Brownian motion is the same as performing a random walk (a)."
- Specular--diffuse--specular (SDS) paths: Light transport paths with a specular-diffuse-specular interaction sequence that are hard to sample. "specular--diffuse--specular (SDS) paths"
- Stationary distribution: The invariant distribution of a Markov chain toward which it converges under mild conditions. "Ensure that the Markov chain has the target distribution as its stationary distribution."
- Symplectic integrators: Numerical integrators that preserve the geometric structure (volume) of Hamiltonian systems, crucial for stable HMC. "symplectic integrators~\citep{leimkuhler2005hamiltonian,hairer2013geometric}."
- Tempered distribution: A temperature-adjusted target used in annealing to flatten or sharpen the landscape. "The tempered distribution is given by: ."
- Typical set: The high-probability region of a distribution where efficient exploration should concentrate. "the geometry of the typical set (the red rings in~\cref{fig:langevin_hmc}b,c)."
- Variance reduction: Techniques that reduce estimator variance to achieve faster convergence in Monte Carlo. "Several variance reduction strategies are proposed in the literature~\cite{veach1998thesis}."
- Variational autoencoders (VAEs): Latent-variable generative models trained by maximizing the ELBO. "in~\cref{mcmc_generative} we study variational autoencoders,"
- Variational diffusion models: Diffusion-based generative models derived from variational principles. "their connection to variational diffusion models."
- Wiener process: The standard Brownian motion process used to model stochastic noise in SDEs. " is a Wiener process or Brownian motion,"
Collections
Sign up for free to add this paper to one or more collections.
