LOTION: Smoothing the Optimization Landscape for Quantized Training (2510.08757v1)
Abstract: Optimizing neural networks for quantized objectives is fundamentally challenging because the quantizer is piece-wise constant, yielding zero gradients everywhere except at quantization thresholds where the derivative is undefined. Most existing methods deal with this issue by relaxing gradient computations with techniques like Straight Through Estimators (STE) and do not provide any guarantees of convergence. In this work, taking inspiration from Nesterov smoothing, we approximate the quantized loss surface with a continuous loss surface. In particular, we introduce LOTION, \textbf{L}ow-precision \textbf{O}ptimization via s\textbf{T}ochastic-no\textbf{I}se sm\textbf{O}othi\textbf{N}g, a principled smoothing framework that replaces the raw quantized loss with its expectation under unbiased randomized-rounding noise. In this framework, standard optimizers are guaranteed to converge to a local minimum of the loss surface. Moreover, when using noise derived from stochastic rounding, we show that the global minima of the original quantized loss are preserved. We empirically demonstrate that this method outperforms standard QAT on synthetic testbeds and on 150M- and 300M- parameter LLMs.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What this paper is about
This paper introduces a new way to train neural networks that will later be run using very few bits (low precision). Using fewer bits makes models smaller and faster, but it also makes training harder because the math becomes “jumpy” and breaks the usual tools for learning. The authors propose LOTION, a method that smooths out those jumps so standard training methods work reliably and give better results.
The big questions the paper asks
- How can we train models that will be quantized (stored with few bits) without running into mathematical problems that make learning unstable?
- Can we create a smooth version of the “quantized” training goal so normal optimizers (like the ones used every day in deep learning) can still find good solutions?
- Will this approach keep the same best solutions (global minima) as the original quantized problem?
- Does this method actually improve real models, including LLMs, at very low precision like 4 or 8 bits?
How the method works (in everyday terms)
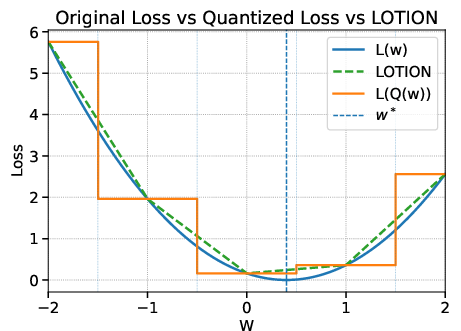
Training a model is like rolling a ball down a hill to the lowest point. When you quantize (use fewer bits), the hill turns into a staircase: flat steps with sudden drops. On flat steps, the ball doesn’t know where to go (the gradient is zero), and at the edges the slope is undefined. That breaks normal training.
LOTION turns the staircase back into a gentle ramp by adding a tiny, smart “shake” before measuring the loss:
- Quantization: This is like rounding each number to the nearest slot in a small set (like rounding prices to the nearest dollar). With very low precision (like 4 bits), you have very few slots, so rounding is aggressive.
- Straight-Through Estimator (STE): A common trick that pretends the rounding didn’t happen when computing gradients. It often works but can be unstable and has no guarantees.
- Randomized rounding: Instead of always rounding to the nearest slot, you flip a biased coin to round up or down. The bias depends on how close you are to each slot, so the average of many coin flips equals the original value. That’s called “unbiased.”
- Smoothing the loss: LOTION doesn’t change the gradient rule. It changes the loss you optimize. It replaces the raw quantized loss with its expected value under randomized rounding. In plain words, it trains on “the average loss you’d get if you applied tiny random roundings,” which turns the staircase into an almost-smooth surface.
- Why this helps: A smooth surface gives meaningful gradients almost everywhere, so standard optimizers (SGD, Adam, second-order methods) can move in the right direction and come with known convergence guarantees.
A helpful mental picture: Imagine your model’s loss landscape is bumpy. LOTION gently blurs it by taking an average over tiny random nudges. That blur makes the path downhill clearer without changing where the very lowest points are.
A bit more detail (without heavy math)
- The paper proves two friendly properties:
- Continuity: The “smoothed” loss is continuous (no sudden jumps), and differentiable almost everywhere.
- Global minima preserved: The best solutions of the smoothed problem are the same as the best solutions of the original quantized loss. So you’re not optimizing the wrong thing.
- Second-order view: The authors show that smoothing behaves like adding a smart penalty (a “curvature-aware regularizer”). If a direction in the loss landscape is very sharp (the surface curves a lot), LOTION penalizes stepping in that direction. This reduces instability. They use the Gauss–Newton approximation (a standard second-order tool) to keep this penalty positive and practical.
- Implementation: You can compute the needed regularizer with information similar to what Adam tracks (squared gradients), so it’s practical even for large models.
What they found and why it matters
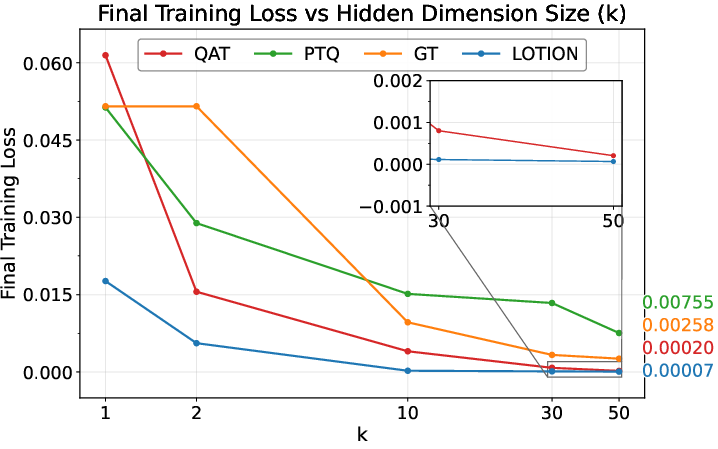
Across small synthetic tests and real LLMs, LOTION beat common baselines:
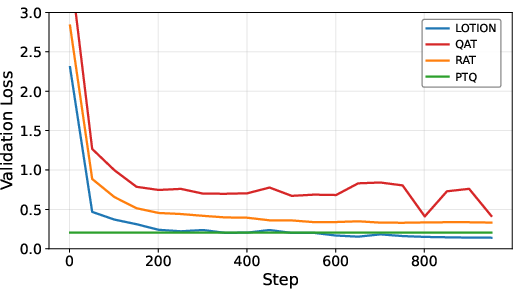
- On a simple linear regression task (a controlled testbed), LOTION achieved lower quantized validation loss than:
- PTQ (post-training quantization), which trains fully and quantizes after
- QAT (quantization-aware training) with STE, which often becomes jagged and stalls at very low precision
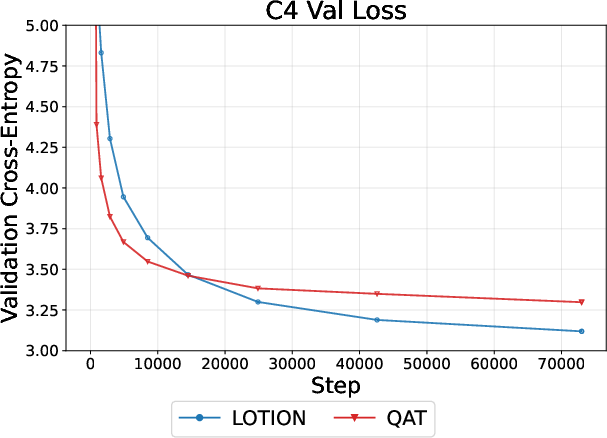
- On 150M- and 300M-parameter LLMs trained on real data:
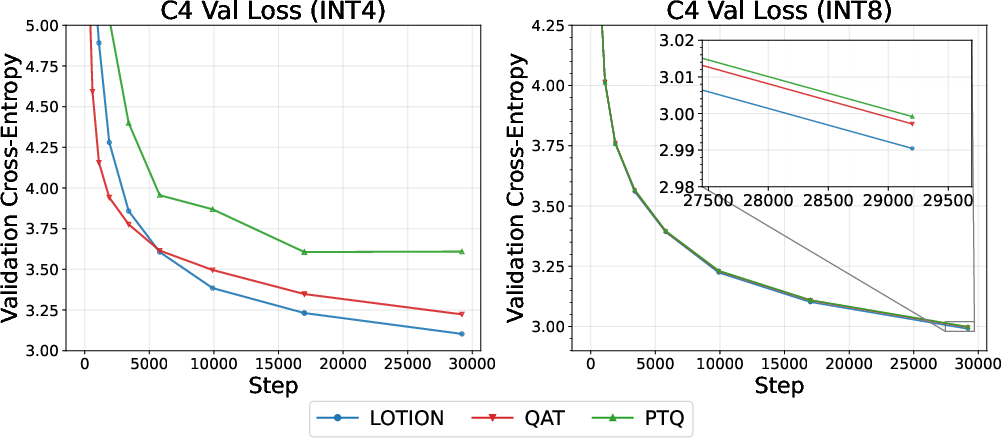
- At INT4 (very low precision), LOTION consistently reduced validation loss more than QAT and PTQ.
- At INT8, LOTION still performed better than baselines.
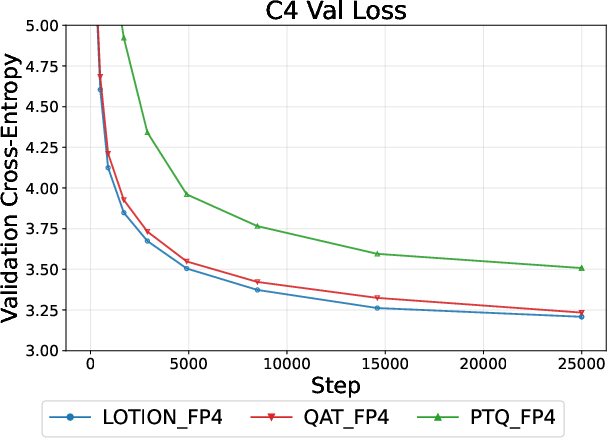
- Even with FP4 (a more forgiving, non-uniform format), LOTION provided noticeable gains over QAT and PTQ.
- Stability: QAT curves often looked noisy and plateaued, while LOTION kept improving, especially at 4-bit precision where training is hardest.
- Guarantees: Because LOTION smooths the loss directly, it inherits convergence guarantees from standard optimization, unlike STE-based methods.
Why this is important:
- Low-precision models are faster and cheaper to run, especially for big LLMs where memory traffic is the bottleneck. Better training at 4–8 bits means more efficient deployment without losing accuracy.
- LOTION is principled (backed by proofs), simple (no extra learned knobs), and works with many rounding schemes.
What this could mean in the future
- Better, cheaper AI: Training directly for low-precision performance means you can serve large models faster and at lower cost, while keeping quality high.
- Fewer hacks: LOTION avoids heuristic gradient tricks and gives a clear, transparent connection between quantization noise and loss curvature.
- Broad compatibility: It works with standard optimizers and various quantization formats (INT4, INT8, FP4), making it easy to adopt.
- Next steps:
- Extend from weight quantization to activation quantization for even bigger speedups.
- Explore other noise choices that keep the same best solutions but make the surface even smoother everywhere.
- Refine the curvature estimates to further stabilize training without much overhead.
In short, LOTION smooths out the nasty parts of quantized training in a mathematically clean way. It keeps the good solutions, makes optimization behave nicely, and improves performance in practice—especially where low precision is most challenging.
Knowledge Gaps
Below is a single, consolidated list of concrete knowledge gaps, limitations, and open questions that remain unresolved by the paper. Each item is phrased to be directly actionable for future research.
- Formal convergence: Provide a full proof (beyond citation to general nonsmooth results) that the LOTION objective with weight-dependent, blockwise absmax scales is “tame” or otherwise satisfies the assumptions required for the cited non-smooth convergence guarantees, including mini-batch stochasticity and moving scales.
- Boundary non-smoothness: The smoothed objective remains non-differentiable at quantization cell boundaries; characterize how often training encounters these boundaries, the impact on convergence, and whether alternative noise distributions can deliver fully smooth objectives while preserving global minima.
- Preservation of minima beyond unbiased RR: The global-minima preservation is proved for unbiased randomized rounding that collapses to a delta on exact codebook points; determine whether this property extends to common practical quantizers with clipping, asymmetric zero-points, or learned scales.
- Approximation gap of the training objective: The algorithm actually optimizes a Gauss–Newton-diagonal (empirical Fisher) regularized surrogate with a tunable weight λ, not the exact E[L(q)]; quantify the bias introduced by (i) Gauss–Newton substitution, (ii) diagonal truncation, and (iii) λ-scaling, and establish conditions under which this surrogate remains faithful to the exact smoothed loss.
- Gradient correctness through scales: Block absmax scales are non-smooth functions of w (argmax and absolute value), yet gradients of the surrogate depend on these scales; derive and validate correct and stable gradient formulas (or subgradients) through the scales, or propose smooth approximations to absmax that preserve guarantees.
- Covariance structure under shared scales: The theory assumes independent per-coordinate rounding, but shared scales couple coordinates via sB; analyze whether off-diagonal terms in Cov[ε] can emerge (e.g., when scale changes) and the effect on the regularizer and optimization.
- Unbiased RR for non-uniform quantizers: Construct and analyze unbiased randomized rounding for non-uniform formats (e.g., FP4 with exponent/mantissa spacing), and derive closed-form σi2 for those formats; validate that minima-preservation and continuity lemmas still hold.
- Clipping-aware smoothing: Many high-quality INT/PTQ schemes rely on clipping to minimize MSE; extend LOTION to clipped quantizers and determine whether global-minima preservation persists, or specify trade-offs introduced by clipping.
- Activation and gradient quantization: The method is evaluated for weight-only quantization; extend and analyze LOTION for activation and/or gradient quantization (including backprop quantization), especially under dynamic activation ranges and layer normalization.
- Scale learning within LOTION: Incorporate learnable scales (per-channel/per-group/per-tensor) into the smoothed objective and paper joint optimization stability, gradient flow through scale parameters, and whether learned scales erode the minima-preservation guarantees.
- Smoothing schedule and λ selection: Provide principled guidance (or adaptive rules) for setting/annealing λ and for scaling the regularization as training progresses, ideally with theoretical bounds or automatic tuning criteria tied to curvature and quantization resolution.
- Error bounds beyond second order: Quantify the O(E[∥ε∥3]) remainder term in the Taylor expansion for realistic quantization noise; bound the mismatch between the second-order approximation and the exact smoothed loss during training.
- Robustness to distribution shift: Evaluate whether LOTION-trained models retain their quantization robustness under domain shift or changing sequence length, and characterize when smoothing-induced regularization helps or hurts generalization.
- Trade-off with full-precision accuracy: Report and analyze the Pareto frontier between full-precision validation loss and quantized validation loss to understand whether improvements in quantized loss come at a cost in FP32 performance.
- Stronger and broader baselines: Compare against state-of-the-art QAT/PTQ methods that learn scales and/or clipping (e.g., LSQ/LSQ+, PACT, AdaRound/Adaptive Rounding variants, NIPQ) across identical settings, including mixed-precision allocation baselines.
- Bit-extreme regimes: Test and analyze performance at very low precisions (3-, 2-, and 1-bit) where STE methods often fail, to assess LOTION’s stability and whether the smoothing still preserves desirable minima or induces degenerate solutions.
- Architectural and task diversity: Validate on broader architectures and modalities (e.g., vision CNNs/ViTs, speech, RL) and tasks beyond pretraining loss (e.g., downstream NLP benchmarks), including fine-tuning scenarios and instruction-tuning.
- Seed and hyperparameter sensitivity: Quantify variance across seeds and hyperparameters (optimizer choice, LR schedules, block sizes, calibration data size for PTQ), and provide robustness analyses and confidence intervals.
- Block size and grouping effects: Systematically paper how block size (per-tensor, per-channel, per-group) affects σi2, the regularizer, and final quantized accuracy, including the interplay with outliers and heavy-tailed weight distributions.
- Deployment realism: Move beyond simulated quantization to on-device integer/fp4 execution; measure end-to-end latency, bandwidth, and energy gains, and verify that training with randomized-rounding-based smoothing translates into real deployment benefits.
- Evaluation with deterministic quantization: Clarify and quantify the potential train–test mismatch between training under randomized rounding and deployment under deterministic RTN (or vice versa), and provide recipes to “de-randomize” at inference without loss.
- Computational overhead: Measure the extra cost of estimating the diagonal Gauss–Newton/empirical Fisher and σi2 at scale; profile training-time slowdowns and memory overhead, and explore low-cost surrogates with similar effectiveness.
- Off-the-shelf optimizer compatibility: Although the paper claims standard optimizers apply, provide empirical and theoretical analysis of optimizer interactions (AdamW, Sophia, Lion, second-order methods), including any stability constraints unique to the smoothed objective.
- Theoretical characterization of local minima: While global minima are preserved under assumptions, characterize how smoothing reshapes local minima and saddle points, and whether it can introduce spurious attractors that impede reaching good quantized solutions.
Glossary
- Absolute maximum quantization: A block-wise scaling scheme that uses the largest absolute value in a block to set the scale, preventing overflow in integer formats. "absolute maximum quantization method described in LLM.int8()"
- Bandwidth-bound: A regime where execution speed is limited by memory bandwidth rather than compute, common in LLM inference. "inference is overwhelmingly bandwidth-bound"
- Codebook: The finite set of representable quantized values to which parameters are mapped. "every forward pass maps weights according to a finite codebook"
- Curvature-aware regularizer: A regularization term weighted by curvature (e.g., Hessian or Gauss–Newton), penalizing sharp directions to stabilize training. "can be interpreted as a curvature-aware regularizer"
- Empirical Fisher approximation: A practical approximation of the Fisher information (often its diagonal) computed from squared gradients. "we can use the empirical Fisher approximation by accumulating the square of the gradients observed in practice as done by Adam"
- Fine-grained shared-scale: A quantization format where parameters are partitioned into blocks that share a single scale, improving range utilization. "the FP8 \"fineâgrained sharedâscale\" format adopted by DeepSeek"
- FP4: A 4-bit floating-point precision format with non-uniform levels that better capture small values and outliers. "Quantized validation loss at FP4 precision"
- FP8: An 8-bit floating-point format used in modern accelerators for efficient training and inference. "the FP8 \"fineâgrained sharedâscale\" format adopted by DeepSeek"
- Gauss–Newton matrix: A positive semidefinite approximation to the Hessian formed from Jacobians and the loss curvature in output space. "we therefore substitute it with the positive-semidefinite GaussâNewton matrix."
- Hessian trace: The sum of the diagonal elements (or eigenvalues) of the Hessian, used to quantify layer-wise curvature and sensitivity. "Hessian trace~\citep{dong2019hawq}"
- Hutchinson-based Hessian trace approximations: Stochastic methods for estimating the trace of the Hessian efficiently using random probe vectors. "Hutchinson-based Hessian trace approximations~\citep{zhou2020adaptive}."
- INT4: A 4-bit signed integer quantization format for weights/activations, offering high compression at the cost of increased error. "at INT4 precision"
- INT8: An 8-bit signed integer quantization format widely used for efficient inference with moderate accuracy loss. "INT8 (Right) precision"
- Lattice (quantization lattice): The grid of quantized points determined by scales and bit-widths, which can change during optimization. "the quantization lattice moves as optimization proceeds."
- LOTION: A loss-smoothing framework that optimizes the expected quantized loss under unbiased randomized rounding noise, preserving global minima. "LOTION introduces a loss-level smoothing framework that avoids heuristic gradient modifications."
- Measure-zero: A set with zero Lebesgue measure; here, the quantizer’s threshold boundaries where gradients fail to exist. "except on the measure-zero cell boundaries induced by the quantizer"
- Nesterov smoothing: A technique that smooths non-smooth objectives by convolving them with a smooth kernel, enabling gradient-based optimization. "taking inspiration from Nesterov smoothing"
- Non-uniform quantization: A quantization scheme with unevenly spaced levels (e.g., FP4), granting finer resolution near zero. "its non-uniform quantization scheme that can represent small values while accounting for rare large outliers."
- Post-training quantization (PTQ): Quantizing a pretrained model using calibration objectives without modifying the training loop. "Post-training quantization (PTQ) and quantization-aware training (QAT) directly alleviate this burden"
- Quantization-aware training (QAT): Training procedures that simulate quantization effects during forward/backward passes to improve quantized performance. "QAT instead optimizes the quantized objective by relying on the straight-through estimator (STE)"
- Quantization bin: The interval of real values mapped to the same discrete quantized level. "the distance to the lower quantization bin after scaling"
- Quantizer: The operator that maps real-valued parameters to a finite set of representable values, often piece-wise constant. "the quantizer is piece-wise constant"
- Randomized rounding: A probabilistic rounding rule that rounds up or down with probabilities chosen to make the expectation equal to the original value. "Randomized Rounding () is a function from "
- Randomized smoothing: Constructing a smooth surrogate by taking expectations of the loss under a noise distribution. "randomized smoothing~\citep{duchi2012randomized, duchi2012ada}"
- Ridge regularizer: An L2 penalty added to the objective, often improving stability and conditioning. "yields an -style ridge term:"
- Round-to-nearest (RTN): Deterministic rounding to the nearest quantization level. "round-to-nearest (RTN)"
- Rounding-Aware Training (RAT): A training approach that computes gradients at randomly rounded points, akin to QAT but with unbiased rounding noise. "We define an analogous algorithm RAT (Rounding-Aware Training) that computes gradients on randomly rounded points instead."
- Shared scale: A single scaling factor applied to all parameters within a block in fine-grained quantization schemes. "the shared scale of the block being rounded"
- Stochastic rounding: A rounding mechanism that selects adjacent levels with probabilities based on the fractional part, reducing bias. "when using noise derived from stochastic rounding, we show that the global minima of the original quantized loss are preserved."
- Straight-through estimator (STE): A heuristic gradient approximation that treats non-differentiable quantization as identity during backpropagation. "straight-through estimator (STE)--a heuristic gradient approximation"
- Symmetric signed integer quantization: A scheme that uses a symmetric range around zero for signed integers, typically avoiding zero-points. "We study the standard symmetric signed integer quantization method"
- Unbiased randomized rounding: Randomized rounding whose expectation equals the original value, enabling differentiable loss smoothing. "unbiased randomized-rounding noise."
Practical Applications
Immediate Applications
Below are specific, deployable use cases and workflows that directly leverage the paper’s findings on LOTION—loss smoothing via unbiased randomized rounding—and its curvature-aware regularizer.
- Quantization-friendly pretraining and fine-tuning of LLMs for lower-cost inference
- Sectors: software, cloud computing, finance, customer support, healthcare, education
- What: Add the LOTION regularization term (Gauss–Newton or empirical Fisher diagonal) during training to produce checkpoints that quantize to INT4/INT8/FP4 with lower validation loss than PTQ/QAT baselines.
- Tools/Workflows: PyTorch/DeepSpeed training with Adam or Sophia; integration with Hugging Face Transformers; export to TensorRT-LLM or ONNX Runtime; blockwise absmax scaling consistent with shared-scale formats.
- Impact: Higher throughput and lower latency on bandwidth-bound inference; reduced serving costs; improved feasibility of 4-bit weight-only deployment.
- Assumptions/Dependencies:
- Access to training pipeline (pretraining or fine-tuning) and data.
- Hardware and runtime support for INT4/INT8/FP4 inference (e.g., TensorRT, custom kernels).
- Empirical Fisher/Gauss–Newton diagonal estimation overhead is acceptable; regularization strength λ requires light tuning.
- Improved weight-only quantization of medium-scale models on edge devices
- Sectors: mobile and embedded AI, robotics, IoT
- What: Train or fine-tune models with LOTION so weights compress well to 4–8 bits; deploy with weight-only quantization to reduce footprint and energy.
- Tools/Workflows: PyTorch training with LOTION; export quantized weights via RR or RTN; deploy with mobile inference runtimes that support low-precision (e.g., vendor NPUs, custom 4/8-bit matmul kernels).
- Impact: Better on-device accuracy at low precision, improved battery life.
- Assumptions/Dependencies:
- Device runtime must support low-precision GEMMs and memory formats.
- Activation quantization not covered yet; benefits are strongest for weight-only pipelines.
- Drop-in training regularizer for quantization-aware optimization without STE heuristics
- Sectors: software, academia
- What: Replace STE-based QAT with LOTION’s loss smoothing using unbiased randomized rounding, preserving convergence guarantees while avoiding gradient instability at 4-bit.
- Tools/Workflows: Implement per-parameter variance σ_i2 = s_B2 Δ_i(1−Δ_i) from shared scales and fractional bin distances; add 0.5 ∑ g_ii σ_i2 to the loss; reuse standard optimizers and convergence theory.
- Impact: More stable low-precision training; matches quantized loss minima with principled smoothing.
- Assumptions/Dependencies:
- Access to the quantization format details (blockwise scales, lattice).
- Empirical Fisher or Gauss–Newton diagonal approximations available (e.g., gradient-square accumulation).
- Quantization export toolkit that selects rounding schemes to minimize post-quantization loss
- Sectors: MLOps, software
- What: Evaluate RR vs RTN per checkpoint (or layer) and choose the rounding strategy that yields lower validation loss; integrate into CI pipelines.
- Tools/Workflows: Post-training evaluation scripts; per-layer rounding policy selection; automated reporting.
- Impact: Reduced accuracy drop at deployment without retraining.
- Assumptions/Dependencies:
- Validation data available to measure quantized loss.
- Runtime supports the chosen rounding scheme at export.
- Academic baselines and reproducible testbeds for low-precision training
- Sectors: academia
- What: Use the paper’s synthetic quadratic and linear testbeds to benchmark quantization-aware methods; adopt LOTION as a principled baseline with convergence guarantees.
- Tools/Workflows: Reference implementations; curriculum modules on smoothing and randomized rounding; integration into open-source quantization benchmarks.
- Impact: Better scientific rigor; reduced reliance on ad hoc STE choices.
- Assumptions/Dependencies:
- Availability of open-source code or straightforward reimplementation.
Long-Term Applications
These applications require additional research, scaling, hardware support, or ecosystem development to fully realize.
- Joint weight-and-activation quantization training with smoothing
- Sectors: software, energy, edge AI, robotics
- What: Extend LOTION to activation quantization, enabling end-to-end 4-bit inference with stability and convergence guarantees.
- Potential Products/Workflows: “LOTION-X” training recipes that co-smooth weights and activations; per-layer curvature-aware bit allocation.
- Dependencies/Assumptions:
- New theory and algorithms to preserve minima under activation quantization.
- Hardware/runtime support for low-precision activations.
- Hardware support for unbiased randomized rounding (RR) in quantizers
- Sectors: semiconductors, accelerators, system software
- What: Implement RR in hardware quantization units to ensure unbiasedness and reproducibility; support fine-grained shared-scale formats efficiently.
- Potential Products/Workflows: RR-capable cast instructions; noise generators; compiler/runtime hooks for RR during training/export.
- Dependencies/Assumptions:
- ISA/runtime changes and validation; negligible overhead relative to RTN.
- Alignment with emerging formats (FP4/FP8, INT4/INT8).
- Precision-aware scaling laws and AutoML that co-optimize accuracy, cost, and precision
- Sectors: software, cloud, energy
- What: Integrate LOTION into training recipes and meta-optimization loops to jointly select model size, tokens, and precision (cf. “Scaling Laws for Precision”).
- Potential Products/Workflows: AutoML pipelines that tune λ, bit-widths, and scales; forecast serving cost and latency under precision constraints.
- Dependencies/Assumptions:
- Robust modeling of accuracy vs precision vs cost; standardized benchmarks; large-scale experiments.
- Standardization of quantization policies and rounding in ML deployment stacks
- Sectors: policy, standards bodies, cloud platforms
- What: Define best practices for unbiased RR, scale management, and curvature-aware regularization in training; include guidance in deployment standards and audits.
- Potential Products/Workflows: Vendor-neutral specs for rounding policies; procurement guidelines that prefer quantization-aware training with convergence guarantees.
- Dependencies/Assumptions:
- Consensus across vendors and platforms; demonstrable energy savings and accuracy retention.
- Curvature-aware bit allocation and noise shaping
- Sectors: software, hardware co-design
- What: Use the Gauss–Newton diagonal to dynamically allocate bits per layer/parameter block and shape quantization noise toward flatter directions.
- Potential Products/Workflows: “LOTION-BitAllocator” integrated into training and export; layer-wise precision scheduling.
- Dependencies/Assumptions:
- Accurate curvature estimation at scale; fast per-layer decision-making; compatibility with mixed-precision kernels.
- Robustness and generalization improvements via principled smoothing
- Sectors: academia, safety-critical applications
- What: Investigate whether LOTION’s curvature-aware smoothing confers robustness to model perturbations beyond quantization (e.g., weight noise, mild adversarial compression).
- Potential Products/Workflows: Regularization modules for safety-critical ML; certified tolerance to compression-induced perturbations.
- Dependencies/Assumptions:
- Empirical and theoretical validation; domain-specific safety standards.
Notes on Feasibility and Assumptions Across Applications
- LOTION’s guarantees rely on unbiased randomized rounding and the continuity/local boundedness properties of the RR distribution; practical deployment often uses RTN, so hardware/software adoption of RR improves fidelity to the theory.
- The curvature-aware term needs diagonal Gauss–Newton or empirical Fisher approximations; these require gradient-square accumulation and introduce small memory/compute overhead and a tuning parameter λ.
- Demonstrated gains are strongest for weight-only quantization; activation quantization remains a research direction.
- Real-world inference throughput and energy benefits depend on low-precision kernel availability and memory bandwidth characteristics of the target hardware.
Collections
Sign up for free to add this paper to one or more collections.