Parallel Spooky Pebbling Makes Regev Factoring More Practical (2510.08432v1)

Abstract: "Pebble games," an abstraction from classical reversible computing, have found use in the design of quantum circuits for inherently sequential tasks. Gidney showed that allowing Hadamard basis measurements during pebble games can dramatically improve costs -- an extension termed "spooky pebble games" because the measurements leave temporary phase errors called ghosts. In this work, we define and study parallel spooky pebble games. Previous work by Blocki, Holman, and Lee (TCC 2022) and Gidney studied the benefits offered by either parallelism or spookiness individually; here we show that these resources can yield impressive gains when used together. First, we show by construction that a line graph of length $\ell$ can be pebbled in depth $2\ell$ (which is exactly optimal) using space $\leq 2.47\log \ell$. Then, to explore pebbling schemes using even less space, we use a highly optimized $A^*$ search implemented in Julia to find the lowest-depth parallel spooky pebbling possible for a range of concrete line graph lengths $\ell$ given a constant number of pebbles $s$. We show that these techniques can be applied to Regev's factoring algorithm (Journal of the ACM 2025) to significantly reduce the cost of its arithmetic. For example, we find that 4096-bit integers $N$ can be factored in multiplication depth 193, which outperforms the 680 required of previous variants of Regev and the 444 reported by Eker{\aa} and G\"artner for Shor's algorithm (IACR Communications in Cryptology 2025). While space-optimized implementations of Shor's algorithm remain likely the best candidates for first quantum factorization of large integers, our results show that Regev's algorithm may have practical importance in the future, especially given the possibility of further optimization. Finally, we believe our pebbling techniques will find applications in quantum cryptanalysis beyond integer factorization.

• The paper introduces parallel spooky pebbling as a novel framework that combines mid-circuit measurements with parallel operations to optimize quantum factoring.
• It formalizes pebble games on line graphs using a recursive Fibonacci-like strategy to achieve optimal depth with near-optimal space usage, validated by an A* search.
• The approach dramatically reduces multiplication depth in quantum factoring, lowering 4096-bit integer depth from 680 to 193 while maintaining practical qubit counts.

Parallel Spooky Pebbling and Its Application to Regev Factoring

Introduction and Motivation

This paper introduces and analyzes the concept of parallel spooky pebbling, a new abstraction that combines two previously distinct resources in reversible and quantum computation: parallelism and "spookiness" (mid-circuit measurement with phase errors). The motivation is to optimize the implementation of inherently sequential computations—such as repeated squaring in modular exponentiation—on quantum computers, with a particular focus on improving the practicality of Regev's quantum factoring algorithm.

Pebble games have long served as a model for understanding the space-time tradeoffs in reversible computation. In the quantum setting, Gidney's "spooky pebble games" leverage mid-circuit measurements to reduce space at the cost of introducing correctable phase errors. Parallel pebble games, on the other hand, allow multiple pebbling moves in a single time step, reducing depth at the cost of increased space. This work is the first to systematically combine these two resources, demonstrating that their synergy yields strictly better tradeoffs than either alone.

Parallel Spooky Pebbling: Model and Main Results

The paper formalizes parallel spooky pebbling games on line graphs, where each vertex represents a computational step (e.g., an iteration of $H$ in $H^\ell(x)$), and pebbles represent the storage of intermediate results. The key operations are:

• Pebble(i): Compute and store the result at position $i$.
• Unpebble(i): Uncompute and free the result at position $i$.
• Ghost(i): Measure and remove the result at position $i$, introducing a phase error ("ghost") that must be corrected later.

Parallelism allows multiple non-interfering pebble/unpebble operations per time step, while ghosting can be performed in parallel without restriction.

The main technical result is a recursive construction (based on a Fibonacci-like sequence) that achieves optimal depth $2\ell$ for a line graph of length $\ell$ using only $\approx 2.47 \log \ell$ pebbles. This matches the best possible depth (as shown by a lower bound) and nearly matches the best possible space up to constant factors.

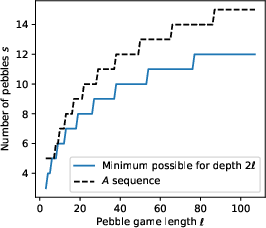
Figure 1: Results of the $A^*$ search for optimal parallel pebble games. The left plot shows the minimum number of pebbles $s$ needed to achieve optimal depth $2\ell$, compared to the theoretical construction; the right plot shows achievable depth as a function of $\ell$ for fixed $s$.

The authors also provide a highly optimized Julia implementation of an $A^*$ search to find optimal pebbling strategies for concrete values of $\ell$ and $s$, supporting weighted cost metrics to account for non-uniform space requirements across pebble positions.

Application to Regev's Factoring Algorithm

The most significant application is to Regev's quantum factoring algorithm, which previously suffered from high space requirements due to the need to store many intermediate results in repeated squaring. Prior approaches either used space-inefficient square-and-multiply or space-efficient but depth-inefficient Fibonacci-based exponentiation.

By recasting the modular exponentiation as a parallel spooky pebbling game, the authors achieve a dramatic reduction in the multiplication depth required for factoring large integers. For example, factoring a 4096-bit integer $N$ can be performed in multiplication depth 193, compared to 444 for the best-known Shor implementation and 680 for previous Regev variants.

The implementation leverages several optimizations:

• Windowing: Batching updates to reduce the number of expensive multiplications.
• Measurement-based uncomputation: Ghosting intermediate results to minimize ancilla usage.
• Ancilla-aware pebbling: Incorporating the varying space cost of different pebble positions into the pebbling optimization.
• In-place classical-quantum multiplication: Using Gidney's low-space adder to further reduce space overhead.

The result is a family of circuits that, for practical problem sizes, outperform both Shor and previous Regev implementations in depth, with a moderate increase in qubit count (e.g., $7n$–$15n$ qubits for $n$-bit factoring).

Tradeoffs, Numerical Results, and Practical Implications

The paper provides detailed numerical results for $n=2048$ and $n=4096$-bit factoring, comparing:

• Shor's algorithm (with and without windowing)
• Regev's algorithm with Fibonacci-based arithmetic
• Regev's algorithm with parallel spooky pebbling

The key findings are:

• Depth: Parallel spooky pebbling achieves the lowest multiplication depth per run, outperforming both Shor and Fibonacci-based Regev circuits.
• Total multiplications: The total number of multiplications per run is also reduced, with only a small gap between depth and total count (unlike the Fibonacci case).
• Space: While not as space-efficient as Shor, the qubit count is significantly lower than previous Regev implementations and is within a practical range for future quantum hardware.
• Classical postprocessing: Increasing the power of the classical lattice reduction (BKZ block size) yields only marginal improvements in quantum resource requirements, suggesting diminishing returns for more aggressive classical postprocessing.

Theoretical and Practical Implications

Theoretically, the work establishes that the combination of parallelism and spookiness in pebble games achieves the best possible asymptotic tradeoff between space and depth for line graphs, up to constant factors. The recursive construction and the $A^*$ search methodology provide a toolkit for optimizing other sequential quantum algorithms.

Practically, the results suggest that Regev's algorithm, previously considered impractical for large $n$ due to space overhead, may become competitive with Shor's algorithm for integer factorization, especially in scenarios where circuit depth is the limiting factor (e.g., near-term quantum devices with limited coherence times). The techniques are also likely to be applicable to other cryptanalytic tasks and sequential quantum computations, such as time-lock puzzles and proofs of work.

Future Directions

Potential avenues for further research include:

• Tighter constant-factor improvements in pebbling space via further optimization of the recursive construction or the $A^*$ search.
• Application to other graph topologies beyond line graphs, relevant for more complex sequential computations.
• Integration with error-corrected quantum architectures, leveraging the centrality of mid-circuit measurement in fault-tolerant quantum computing.
• Exploration of weighted pebbling games for tasks with highly non-uniform space or gate costs.

Conclusion

This work demonstrates that parallel spooky pebbling provides a powerful new abstraction for optimizing sequential quantum computations, achieving optimal depth with near-optimal space. Its application to Regev's factoring algorithm yields concrete improvements over both Shor's algorithm and previous Regev implementations, suggesting that the practical landscape of quantum cryptanalysis may shift as these techniques are further refined and adopted. The generality of the pebbling framework and the availability of optimized search tools position this approach as a foundational technique for future quantum algorithm engineering.