2000 character limit reached
Dual Goal Representations (2510.06714v1)
Published 8 Oct 2025 in cs.LG and cs.AI
Abstract: In this work, we introduce dual goal representations for goal-conditioned reinforcement learning (GCRL). A dual goal representation characterizes a state by "the set of temporal distances from all other states"; in other words, it encodes a state through its relations to every other state, measured by temporal distance. This representation provides several appealing theoretical properties. First, it depends only on the intrinsic dynamics of the environment and is invariant to the original state representation. Second, it contains provably sufficient information to recover an optimal goal-reaching policy, while being able to filter out exogenous noise. Based on this concept, we develop a practical goal representation learning method that can be combined with any existing GCRL algorithm. Through diverse experiments on the OGBench task suite, we empirically show that dual goal representations consistently improve offline goal-reaching performance across 20 state- and pixel-based tasks.
Summary
- The paper demonstrates that dual goal representations, encoding temporal distances, ensure sufficiency and noise invariance in goal-conditioned RL.
- The method employs neural network approximations to model temporal distances, significantly accelerating policy learning in offline settings.
- Empirical evaluations show robust improvements in state- and pixel-based tasks, outperforming traditional approaches and handling noisy observations.
Dual Goal Representations: Theory, Algorithms, and Empirical Evaluation
Introduction
This paper introduces the concept of dual goal representations for goal-conditioned reinforcement learning (GCRL). The central idea is to represent a goal not by its raw state observation, but by the set of temporal distances from all other states in the environment. This functional representation is shown to possess two critical properties: sufficiency (it contains all information necessary to recover an optimal goal-reaching policy) and noise invariance (it is robust to exogenous, uncontrollable noise in the state observations). The authors provide both theoretical justification and practical instantiation of dual goal representations, and demonstrate their empirical effectiveness across a diverse suite of offline goal-reaching tasks.
Figure 1: Dual goal representation encodes a goal as the set of temporal distances from all other states, capturing intrinsic dynamics and discarding exogenous noise.
Theoretical Foundations
The dual goal representation is formally defined as a functional , where is the optimal temporal distance from state to goal . The paper proves two main theorems:
- Sufficiency: There exists a deterministic policy that, given a dual goal representation, can recover the optimal goal-reaching policy for any state-goal pair.
- Noise Invariance: In the exogenous block controlled Markov process (Ex-BCMP) framework, dual goal representations are invariant to exogenous noise; i.e., two observations corresponding to the same latent state yield identical dual representations.
These results establish dual goal representations as both minimal and sufficient for optimal goal-reaching, and robust to irrelevant observation noise.
Practical Instantiation
Directly implementing the functional form of dual goal representations is infeasible for large or continuous state spaces. The authors propose a practical approximation using parameterized neural networks:
- The temporal distance function is modeled as , where and are neural network encoders for states and goals, respectively, and is an aggregation function.
- The inner product is used for its universality and expressiveness.
- Temporal distances are approximated via goal-conditioned value learning (e.g., goal-conditioned IQL), and the goal head is used as the learned dual goal representation.
This representation can be integrated into any downstream GCRL algorithm, such as GCIVL, CRL, or GCFBC, by conditioning policies and value functions on .
Empirical Evaluation
Experiments are conducted on OGBench, a comprehensive suite of state- and pixel-based goal-conditioned tasks spanning robotic navigation and manipulation.
Figure 2: OGBench environments provide diverse state- and pixel-based goal-conditioned tasks for evaluating representation learning in GCRL.
Discrete Puzzle Proof-of-Concept
In tabular "Lights Out" puzzle environments, dual goal representations (using ground-truth temporal distances) substantially accelerate policy learning and improve final performance compared to raw state representations. This demonstrates the value of structured, dynamics-aware goal encoding.
State-Based and Pixel-Based Tasks
Across 20 OGBench tasks, dual goal representations consistently outperform prior goal representation learning methods (VIB, VIP, TRA, BYOL-) and the raw state baseline. Notably, dual representations yield strong improvements in complex manipulation tasks (e.g., cube rearrangement), and exhibit robustness to noisy goal observations.
Ablations and Analysis
- Noise Robustness: Dual goal representations maintain performance under significant goal noise, validating theoretical noise invariance.
- Aggregation Function: The inner product parameterization outperforms metric-based parameterizations (e.g., ), likely due to its universality.
- Policy Extraction: Directly extracting policies from the temporal distance function is suboptimal; a separate downstream GCRL policy network yields better results.
- Fusion in Visual Tasks: Early fusion of state and goal images is critical for pixel-based tasks; late fusion (required for representation-based methods) degrades performance in certain environments, indicating a limitation and direction for future work.
Implementation Considerations
- Computational Requirements: Dual goal representation learning requires training an additional goal-conditioned value function, but is compatible with standard offline RL pipelines.
- Scalability: The method scales to high-dimensional state and goal spaces via neural network parameterization.
- Integration: Dual representations can be used with any GCRL algorithm, and do not require environment interaction beyond the offline dataset.
- Limitations: In pixel-based tasks where early fusion is critical, representation-based methods may underperform; architectural modifications may be necessary.
Implications and Future Directions
The dual goal representation framework provides a principled approach to goal encoding in GCRL, with strong theoretical guarantees and empirical performance. Its robustness to noise and universality make it attractive for real-world applications in robotics and sequential decision making. Future work may explore:
- Joint state-goal representations for improved fusion in visual tasks.
- Extensions to hierarchical or compositional goal representations.
- Applications in online RL and continual learning settings.
- Further analysis of aggregation functions and representation dimensionality.
Conclusion
Dual goal representations offer a theoretically sound and practically effective solution to goal encoding in goal-conditioned RL. By leveraging temporal distances and intrinsic dynamics, they enable robust, generalizable, and efficient policy learning across diverse environments. The framework is broadly applicable and opens new avenues for research in representation learning for RL.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper introduces a new way to describe goals for robots and AI agents that learn by trial and error (reinforcement learning). The new idea is called a dual goal representation. Instead of showing the robot a goal as a picture or a list of numbers (which might include lots of unhelpful details), the goal is described by how long it would take to reach that goal from every possible place. Think of it as a “time-to-get-there” map for that goal. This makes learning faster, more reliable, and more resistant to noise (like messy backgrounds in images).
What questions did the researchers ask?
They focused on two simple but important questions about goal representations (how we describe goals to a learning agent):
- Can the goal description contain just the right information to do the task as well as possible? (Sufficiency)
- Can the goal description ignore useless details, like random visual noise, that don’t affect what the robot can control? (Noise invariance)
They wanted a representation that keeps what matters for reaching the goal and throws away what doesn’t.
How did they paper it?
First, the idea in everyday language:
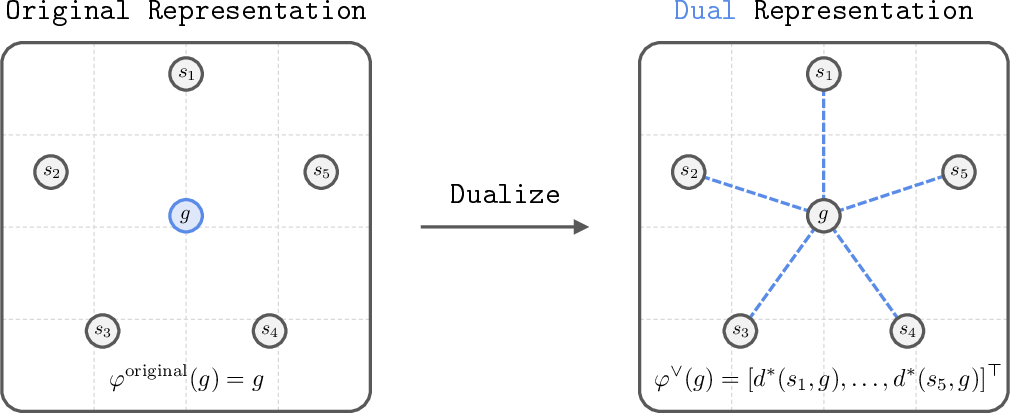
- Imagine a city where you can stand at many different locations (states) and you want to reach a specific restaurant (a goal). A dual goal representation for that restaurant would be a table that tells you, for every location in the city, how long it would take to get to the restaurant. That “time-from-everywhere” table uniquely describes the restaurant in a way that’s useful for planning. It doesn’t care about the restaurant’s photo, the color of the sign, or background noise—it only cares about the city’s road network (the environment’s dynamics).
Then, how they make this practical with computers:
- Real environments have huge numbers of states, so they can’t store a giant “time-from-everywhere” table for every goal. Instead, they train a neural network to approximate the “time-to-goal” using two compact vectors (embeddings): one for the current state and one for the goal.
- The network combines these two vectors with a simple inner product (a dot product) to predict the time-to-goal. If the prediction is accurate for many state–goal pairs, the goal vector must be capturing the right kind of information—the dual goal representation.
- They learn this using offline data (previously collected experience), with a value-learning method (a type of algorithm that learns how good it is to be in a state when trying to reach a goal). Specifically, they use a strong modern method called Implicit Q-Learning adapted for goals.
- After training the “time-to-goal” predictor, they keep the goal vector as the new goal representation and plug it into any goal-reaching algorithm to train a policy (a rule for choosing actions).
In short, the approach has two phases:
- Learn time-to-goal from data using a network with a state head and a goal head, combined by a dot product.
- Use the learned goal head as the goal representation when training the final goal-reaching policy.
What did they find, and why is it important?
Main theoretical results:
- Sufficiency: If you describe a goal by its “time-from-everywhere” map, that’s enough information to recover an optimal way of reaching it. In other words, you don’t lose any decision-making power by switching to this representation.
- Noise invariance: If two images look different but actually come from the same underlying situation (say, same object positions, just different lighting), they get the same dual representation. This helps ignore irrelevant visual noise.
Main practical results (experiments):
- In a puzzle game (“Lights Out”), using dual representations made learning much faster and better than using raw states.
- On a large benchmark suite with 20 tasks (robots navigating mazes, moving objects, playing with cubes, etc.), dual goal representations consistently improved performance across many tasks, often beating other modern representation-learning methods.
- In visual tasks (using images), dual goal representations were best in 5 of 7 tasks. They—and all other methods—struggled on two image-based puzzles, likely because of how image inputs are combined (“late fusion” vs. “early fusion”; the latter usually works better for images but is trickier with separate goal embeddings).
- Robustness: When the goals were made noisier (for example, adding random noise to goal images), policies using dual goal representations stayed strong more often than those using raw goals.
- Design choices: Using the dot product to combine state and goal vectors worked better than using a simple distance (like Euclidean distance). Also, directly turning the time-to-goal predictor into a policy wasn’t as good as training a separate policy on top of the learned representations—so the two-step approach works best.
Why this matters:
- Better goal representations make learning faster and more reliable, especially when data is noisy or when goals look different on the surface but mean the same thing.
- The method is “plug-and-play”: it can be added to many existing goal-reaching algorithms to boost performance.
What could this change in the future?
- More robust robots: Agents could handle messy, real-world inputs (like cluttered backgrounds or lighting changes) because the dual representation focuses on what the robot can control and how to get there.
- Easier generalization: Since the representation is tied to the environment’s dynamics (how actions change the world) rather than raw appearances, agents may adapt better to new goals they haven’t seen before.
- Broad compatibility: The idea is algorithm-agnostic, so it can improve many different goal-reaching methods.
- Next steps: Make the approach work even better with images (for example, by designing state-aware goal representations or improved fusion methods), and explore more complex real-world tasks.
Overall, the paper shows that describing goals by “how long it takes to get there from everywhere” is both a powerful theory and a practical tool for building better goal-reaching AI.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what remains missing, uncertain, or unexplored in the paper, framed to be actionable for future research:
- Formal extension of theoretical results to continuous state and action spaces
- The sufficiency and noise-invariance theorems are stated for discrete spaces with a note that “results can be extended” to continuous spaces, but no formal proofs, conditions, or construction are provided.
- Open question: Under what topological or measure-theoretic assumptions on do sufficiency and noise invariance hold, and what is the precise functional approximation class needed?
- Realism of the Ex-BCMP assumptions for noise invariance
- Invariance requires observation emissions with disjoint supports and a deterministic latent mapping , which is often violated in realistic vision-based tasks (e.g., occlusions, aliasing, partial observability).
- Open question: Can noise invariance be established (or relaxed) under overlapping emissions, stochastic mappings, or partial observability (POMDPs)?
- Handling unreachable or rarely reached goals
- The definition is undefined for and ill-conditioned when is very small; the paper does not discuss how unreachable goals or poor dataset coverage affect representation learning.
- Open question: What are robust surrogates for in the presence of unreachable goals, and how do approximation errors propagate to policy performance?
- Generality beyond “hit-the-goal-once” reward and absorbing goal dynamics
- All theory assumes and absorbing behavior upon reaching the goal; many tasks have success regions, repeated rewards, or shaped rewards.
- Open question: Do sufficiency and noise invariance extend to region goals, tolerance bands, or general reward functions, and how should be redefined?
- Approximation guarantees and error propagation from learned temporal distances
- The practical method learns via GC-IQL but provides no bounds: how errors in translate to suboptimality in downstream policies using .
- Open question: Can we characterize the sample complexity and approximation error of learning and its impact on downstream goal-reaching performance?
- Choice and capacity of the inner product parameterization
- While inner products are claimed “universal,” the paper does not specify required dimensionality, capacity, or regularization to achieve universality in practice, nor how to select .
- Open question: What are principled model-selection criteria (dimension, architecture) and regularizers for stable learning of and that preserve expressivity and avoid degenerate solutions?
- State-conditioned or relational goal representations for visual tasks
- The failure on visual puzzle tasks is attributed to the need for early fusion; the current design forces late fusion via separate goal encoders.
- Open question: Can a state-conditioned goal representation (e.g., cross-attention, concatenation in feature space, conditional encoders) retain dual-representation benefits while enabling early fusion?
- Robustness beyond exogenous goal noise
- Empirical robustness tests add Gaussian noise to goals only; robustness to state noise, temporal drift, sensor occlusions, and endogenous (action-dependent) noise is not studied.
- Open question: How do dual representations perform under broader distribution shifts (state and dynamics) and realistic visual corruptions (blur, occlusion, lighting)?
- Dataset coverage and offline training limitations
- The approach relies on offline data to learn temporal distances; there is no analysis of coverage requirements (e.g., graph connectivity, shortest path coverage) or behavior when coverage is sparse or biased.
- Open question: What coverage metrics predict successful learning of , and can active data selection or dataset repair improve representation quality?
- Scalability and computational trade-offs
- Training two value functions (for and for downstream policy learning) increases computational cost; the paper does not quantify overhead nor interactions between the two training loops (e.g., shared encoders, interference).
- Open question: What are efficient joint-training strategies, and can one reduce compute by distilling into downstream networks without degrading performance?
- Ambiguity in the practical target used for learning
- The paper mentions learning a “transformed variant” of via but does not specify the exact transformation, targets, or stability tricks necessary for reliable estimation across tasks.
- Open question: Which target transformations (e.g., temperature scaling, clipping, log-transform) improve stability and accuracy of temporal distance estimation?
- Policy extraction directly from
- The paper notes degraded performance when extracting policies directly from , but does not explore architectural or training remedies (e.g., auxiliary heads, actor-critic over ).
- Open question: Can we design a richer parameterization or multi-head architecture to allow to serve both as a dual representation learner and a competent policy without separate downstream training?
- Sensitivity to the downstream GCRL algorithm and broader compatibility
- While tested with GCIVL, CRL, and GCFBC, compatibility with planning-based, model-based, or hierarchical GCRL methods is not evaluated.
- Open question: How do dual representations interact with planners or hierarchical controllers (subgoals), and can they improve planning cost heuristics or goal relabeling strategies?
- Real-world validation and partial observability
- All experiments are in simulation; real-robot evaluations, delayed observations, and sensor imperfections are not covered.
- Open question: Do dual goal representations retain benefits on real robots with POMDP dynamics and practical sensing constraints?
- Symmetry, invariance, and structure in representations
- The representation is not explicitly constrained to respect task symmetries (e.g., translation, rotation) or invariances common in robotics tasks.
- Open question: Can incorporating symmetry-aware encoders or group-equivariant architectures enhance generalization and reduce sample complexity?
- Failure analysis on tasks where dual underperforms “Orig”
- In some environments (e.g., antsoccer-arena with GCIVL), dual representations trail the original; reasons (misestimated , representation mismatch, task idiosyncrasies) are not analyzed.
- Open question: What task properties lead to dual underperformance, and can adaptive aggregation functions or task-dependent losses mitigate this?
- Evaluation breadth and statistical rigor
- The paper reports means and CIs but lacks formal significance testing across methods and an analysis of variance across seeds, tasks, and algorithms.
- Open question: Can more rigorous statistical comparisons and broader ablations (e.g., encoder sharing, representation dimension, expectile κ sensitivity) strengthen conclusions?
- Theoretical treatment of stochastic dynamics and risk
- Temporal distances in stochastic environments encode expected time-to-go under optimal policies; the paper does not address variance, risk-sensitive objectives, or multi-modal dynamics.
- Open question: How should dual representations be adapted for risk-aware or distributional objectives (e.g., CVaR), and can they encode higher-order temporal statistics?
- Goal semantics beyond exact-state equality
- Many practical goals are sets (regions), predicates, or task graphs; the formulation assumes exact state equality and one-time success.
- Open question: How to define dual representations for set-valued goals, multi-step tasks, or compositional objectives, and what are the corresponding theoretical guarantees?
Practical Applications
Immediate Applications
The following items describe practical uses that can be deployed now, drawing directly on the paper’s methods and empirical results. For each, we include sector links, potential tools/workflows, and feasibility considerations.
- Robust offline pretraining for goal-conditioned robot policies
- Sector: robotics, logistics, manufacturing
- What: Use dual goal representations (DGR) to pretrain multi-task goal-reaching policies from “play”-style, unlabeled datasets (e.g., navigation to coordinates, pick-and-place, object rearrangement), improving success rates and generalization to unseen goals.
- Workflow: Collect diverse play data → train goal-conditioned IQL to approximate temporal distance → extract the goal head as the DGR → train downstream policy via GCIVL/CRL/GCFBC → evaluate and deploy.
- Tools/products: A PyTorch module implementing f(ψ(s), φ(g)) with inner-product aggregation; a reproducible training script based on OGBench; ROS node for goal encoding and policy conditioning.
- Assumptions/dependencies: Access to offline data covering diverse transitions; reward defined as goal equality (absorbing at goal); environments where state-based observations are available; compute resources for offline training.
- Warehouse and factory robot navigation with improved goal generalization
- Sector: logistics, industrial automation
- What: Pretrain mobile robots (point/ant/humanoid analogs) to navigate mazes/warehouse aisles toward arbitrary coordinates using DGR, with increased robustness to goal-specification noise (e.g., localization jitter).
- Workflow: Map goals to spatial states; train temporal distance via GC-IQL; use inner-product goal embedding in downstream navigation RL (GCIVL or CRL).
- Tools/products: Goal Embedding API service that receives a target coordinate and returns φ(g); integration with mapping/localization stacks.
- Assumptions/dependencies: Reliable mapping from goal observations to latent positions; sufficient coverage of the environment in offline data; safety validation before on-floor deployment.
- Manipulation policies for structured tasks (cube stacking, scene rearrangement)
- Sector: manufacturing, e-commerce fulfiLLMent, consumer robotics
- What: Train arms for multi-object manipulation tasks using DGR to represent end states (target object poses), improving performance and invariance to background visual noise or minor sensor drift.
- Workflow: Play-style data collection (random reach/press/grasp) → DGR training via GC-IQL → downstream policy via GCIVL/GCFBC.
- Tools/products: Manipulation goal encoder integrated into task planners; retraining pipeline for new layouts/objects.
- Assumptions/dependencies: Ex-BCMP-like observation structure (distinct latent states underpin observations); state-based or reliably estimated latent states; availability of diverse play data.
- Noise-robust goal specification in control systems
- Sector: robotics, industrial control, automation
- What: Replace raw goal observations with DGR embeddings to reduce sensitivity to exogenous noise (e.g., lighting changes or camera noise), consistent with the paper’s theoretical and empirical noise-invariance claims.
- Workflow: Inject noise into evaluation goals to test; swap goal inputs with φ(g); monitor robustness improvements.
- Tools/products: Diagnostic toolkit for goal-embedding robustness; automated OOD goal stress tests.
- Assumptions/dependencies: Observation noise matches exogenous patterns covered by Ex-BCMP (distinct latent-state supports); well-trained value function approximations.
- Game AI and simulation agents with structured goal embeddings
- Sector: software, gaming, simulation
- What: Use DGR for grid/world navigation, puzzle-solving, and pathfinding where temporal distances are estimable, accelerating policy learning.
- Workflow: For discrete domains (like “Lights Out”), precompute or learn d*(s,g); use sampled DGR vectors or inner-product embeddings as goal inputs to goal-conditioned DQN/GCIVL.
- Tools/products: Lightweight DGR encoder for turn-based/maze games; benchmarking harness for pathfinding tasks.
- Assumptions/dependencies: Tabular or low-dimensional approximations of d*; consistent reward design (goal absorption).
- Standardized offline GCRL pipeline upgrade
- Sector: ML engineering, RL platforms
- What: Drop-in DGR module combined with any offline GCRL algorithm (GCIVL, CRL, GCFBC) to boost goal-reaching performance with minimal changes.
- Workflow: Wrap existing datasets and training loops to add φ(g) and ψ(s); retain downstream algorithm unchanged.
- Tools/products: Library extension for existing RL frameworks; tutorial notebooks on OGBench tasks.
- Assumptions/dependencies: Model capacity sufficient for inner-product universality; stable value-learning (e.g., expectile loss with target networks).
- Teleoperation assistance and goal-aware feedback
- Sector: robotics, human-in-the-loop systems
- What: Use the learned temporal distance model and DGR to compute progress-to-goal and provide goal-aware hints or autopilot nudges during teleoperation.
- Workflow: Estimate d*(s,g) online via f(ψ(s), φ(g)); surface progress bars/hints; optionally blend with low-level assistance.
- Tools/products: Teleop UI widgets for progress visualization; assistance functions leveraging DGR embeddings.
- Assumptions/dependencies: Reliable on-policy inference of ψ(s); latency budgets for computing f; careful human factors design for assistance blending.
Long-Term Applications
The following applications require further research or engineering, scaling, and/or solving limitations noted in the paper (e.g., pixel-based late-fusion constraints, broader domain assumptions).
- Pixel-based manipulation with state-aware goal encoders
- Sector: robotics, computer vision
- What: Overcome the “early vs. late fusion” limitation by developing state-aware goal encoders (e.g., φ(g|s), cross-attention, shared CNN backbones) so DGR can match or exceed early-fusion performance in visual tasks.
- Tools/products: Vision encoders with state-goal cross-attention; joint training pipelines for φ(g|s) and ψ(s) with GC-IQL; benchmarking suites for pixel-based tasks.
- Assumptions/dependencies: Advances in architecture design to re-enable “early fusion”-like benefits within representation learning; larger pixel datasets.
- Hierarchical RL using DGR for subgoal discovery and curriculum learning
- Sector: robotics, software agents
- What: Use DGR and d*(s,g) to identify intermediate subgoals at bottlenecks or waypoints, building curricula that improve long-horizon performance.
- Tools/products: Subgoal mining utilities from temporal-distance landscapes; hierarchical controllers that condition on φ(g) at multiple levels.
- Assumptions/dependencies: Accurate temporal distance estimation over large state spaces; stable hierarchical training methods.
- Autonomous driving/path-planning with robust goal embeddings
- Sector: automotive, drones
- What: Use DGR for destination encoding and waypoint selection, leveraging noise invariance to reduce sensitivity to sensor perturbations.
- Tools/products: Destination embedding module φ(g) integrated with planners; offline pretraining from human driving datasets.
- Assumptions/dependencies: Safety certification; mapping to latent states with Ex-BCMP-like structure; large-scale datasets and edge-compute hardware.
- Standardized “Goal Embedding” interoperability layer
- Sector: robotics platforms, middleware vendors
- What: Define a cross-robot, cross-software specification for φ(g) goal embeddings (including dimensionality, normalization, and API design) to enable plug-and-play GCRL across devices.
- Tools/products: Open specification and SDKs; converters for common robot frameworks (ROS/ROS2, Isaac, Mujoco-based stacks).
- Assumptions/dependencies: Community adoption; benchmarks demonstrating interoperability benefits.
- Multi-agent coordination via shared goal representations
- Sector: warehouse fleets, collaborative robotics
- What: Coordinate multiple agents by conditioning policies on shared or decomposed goal embeddings (e.g., team tasks requiring synchronized subgoals).
- Tools/products: Multi-agent training frameworks using DGR; goal decomposition and assignment utilities.
- Assumptions/dependencies: Extensions of DGR to multi-agent dynamics; scalable offline datasets capturing coordination behaviors.
- Healthcare and micro-assembly robots with precise target-state control
- Sector: healthcare, semiconductor manufacturing
- What: Apply noise-robust goal embeddings to delicate tasks (e.g., surgical tool positioning, micro-assembly alignment), reducing sensitivity to visual noise and minor perturbations.
- Tools/products: Specialized φ(g) encoders validated under domain-specific noise; safety-monitored offline pretraining.
- Assumptions/dependencies: Regulatory approval; high-fidelity latent state estimation; robust sim-to-real transfer.
- Energy and building control for setpoint-reaching policies
- Sector: energy management, smart buildings
- What: Treat setpoints as goals; use DGR to encode targets and learn policies that robustly reach them under noisy measurements (e.g., HVAC, grid control).
- Tools/products: Control policies trained from historical logs; goal encoders integrated with BMS.
- Assumptions/dependencies: Mapping continuous control to GCRL frameworks; reward shaping beyond strict equality; safety constraints in critical infrastructure.
- RL+LLM agent integration for structured goal conditioning
- Sector: software automation, digital assistants
- What: Combine LLM planners with DGR-conditioned RL controllers, where text-defined goals are grounded into φ(g) to drive low-level execution.
- Tools/products: Goal grounding modules mapping task descriptions to latent goal states; hybrid planners.
- Assumptions/dependencies: Reliable grounding from language to latent states; joint training across modalities.
- Policy guidance and governance for safe offline RL
- Sector: policy/regulation, enterprise risk management
- What: Develop best-practice guidelines for collecting “play” datasets, auditing goal representations for robustness and fairness, and minimizing risky exploration through offline training.
- Tools/products: Data collection standards; robustness audit tooling; documentation templates for compliance.
- Assumptions/dependencies: Industry buy-in; domain-specific safety and privacy constraints.
- Direct policy extraction from temporal distance models at scale
- Sector: robotics, ML systems
- What: Improve direct policy extraction from f(ψ(s), φ(g)) (noted as weaker in experiments) via more expressive architectures or hybrid losses, eventually eliminating separate downstream training.
- Tools/products: Enhanced temporal-distance parameterizations (e.g., bilinear forms, attention); joint optimization schemes.
- Assumptions/dependencies: Architectural advances; large datasets; careful regularization to avoid overfitting.
Cross-cutting dependencies and assumptions that impact feasibility
- Ex-BCMP assumptions: Noise invariance relies on observation distributions from different latent states having disjoint supports and a reliable mapping pℓ(s)→z.
- Reward structure: Many results hinge on r(s,g)=I[s=g] with absorption at the goal; adapting to shaped/continuous rewards needs methodological adjustments.
- Value approximation quality: The effectiveness of DGR depends on accurate temporal distance learning via goal-conditioned IQL and sufficient model capacity (inner-product universality holds only with adequate dimensionality).
- Fusion limitations in vision: Late fusion degrades pixel-based performance; overcoming this requires state-aware goal encoders or architectural changes.
- Dataset diversity: Generalization to unseen goals depends on broad coverage in offline “play” data; sparse or biased datasets may limit performance.
- Compute and tooling: Offline training pipelines require GPUs and mature infrastructure; success is contingent on stable training (e.g., expectile losses, target networks).
Glossary
- absorbing state: A terminal state where the episode ends and no further rewards can be obtained. Example: "assume that the agent enters an absorbing state once it reaches the goal (\ie, it can get a reward of $1$ at most once)."
- aggregation function: A function that combines state and goal representations to produce a scalar (e.g., a temporal distance). Example: "$f: \sR^{N} \times \sR^{N} \to \sR$ is a (simple) aggregation function that combines the information from both heads to compute the temporal distance."
- controlled Markov process (CMP): A Markov decision process without explicit rewards, defined by states, actions, and transition dynamics. Example: "A controlled Markov process (CMP) is defined by the tuple $\gM = (\gS, \gA, p)$."
- contrastive RL (CRL): A reinforcement learning approach that uses contrastive objectives to learn policies or representations. Example: "contrastive RL (CRL)~\citep{crl_eysenbach2022}"
- discount factor: A number in (0,1) that exponentially down-weights future rewards. Example: "where denotes a discount factor"
- dual goal representation: A representation of a goal by its temporal distances from all states, i.e., a functional mapping states to distances. Example: "We call this a dual goal representation."
- emission distribution: The probabilistic mapping from latent states to observable states in an observation model. Example: "$p^e({s} \mid {z}): \gZ \to \Delta(\gS)$ is an observation emission distribution"
- exogenous noise: Observation variations unrelated to the underlying controllable dynamics. Example: "and is able to discard exogenous noise."
- Ex-BCMP (Exogenous block CMP): A framework where observations are noisy emissions of latent states with disjoint supports, enabling noise-invariant analysis. Example: "An Ex-BCMP is defined by a tuple $(\gS, \gZ, \gA, p, p^e, p^d)$"
- expectile loss: A regression loss that generalizes quantiles to expectations at a specified asymmetry level (expectile κ). Example: "where denotes the expectile loss with expectile ~\citep{iql_kostrikov2022}"
- functional: A function that takes a function-like object (here, a state) as input and returns a scalar; in this paper, a mapping from states to temporal distances. Example: "we represent a goal as a functional (\ie, a function from the state space to )"
- goal-conditioned flow BC (GCFBC): A behavioral cloning method that uses flow models conditioned on goals. Example: "goal-conditioned flow BC (GCFBC)~\citep{sharsa_park2025}"
- goal-conditioned IQL (Implicit Q-Learning): An offline RL method adapted to goal-conditioned settings to learn value functions (and here, temporal distances). Example: "In particular, we employ goal-conditioned IQL~\citep{iql_kostrikov2022, ogbench_park2025} to learn "
- goal-conditioned IVL (GCIVL): Goal-conditioned implicit V-learning, a value-based offline RL algorithm for goal-reaching. Example: "goal-conditioned IVL (GCIVL)~\citep{iql_kostrikov2022, ogbench_park2025}"
- goal-conditioned policy: A policy that selects actions based on the current state and a specified goal. Example: "Given a goal-conditioned policy $\pi({a} \mid {s}, {g}): \gS \times \gS \to \Delta(\gA)$"
- goal-conditioned reinforcement learning (GCRL): RL where the agent is trained to reach arbitrary specified goals. Example: "goal-conditioned reinforcement learning (GCRL)~\citep{gcrl_kaelbling1993, ogbench_park2025}."
- Hilbert space: A complete inner-product vector space used in functional analysis and learning theory. Example: "a point in a Hilbert space as a linear functional in its dual space"
- inner product parameterization: Modeling a scalar function as the inner product of two learned embeddings (state and goal). Example: "we use the following inner product parameterization:"
- latent mapping function: A deterministic map from observations to latent states assumed by the Ex-BCMP framework. Example: "and $p^\ell({s}): \gS \to \gZ$ is a latent mapping function"
- offline goal-conditioned RL: Training goal-reaching policies solely from a fixed dataset without environment interaction. Example: "The objective of offline goal-conditioned RL is to find a goal-conditioned policy "
- Riesz representation theorem: A theorem stating that continuous linear functionals on Hilbert spaces can be represented as inner products with a unique element. Example: "the Riesz representation theorem implies that we can uniquely represent a point in a Hilbert space as a linear functional in its dual space"
- target Q network: A slowly updated copy of the Q-function used to stabilize temporal-difference learning. Example: "and denotes the target Q network~\citep{dqn_mnih2013}."
- temporal distance function: A function mapping a state-goal pair to the (discount-based) shortest expected time to reach the goal. Example: "We also define the temporal distance function as ."
- trajectory distribution: The distribution over sequences of states and actions induced by a policy and dynamics. Example: "and denotes the trajectory distribution induced by the policy and transition dynamics."
- transition dynamics kernel: The conditional probability distribution over next states given current state and action. Example: "$p({s'} \mid {s}, {a}): \gS \times \gA \to \Delta(\gS)$ be a transition dynamics kernel"
- universality: The property that a function class can approximate any target function (on compact sets) to arbitrary accuracy. Example: "We note that this inner product form is universal~\citep{metra_park2024}, meaning that it is expressive enough to approximate any two-variable function (on a compact set) up to an arbitrary accuracy."
- variational information bottleneck (VIB): A representation learning objective that compresses inputs while preserving predictive information. Example: "VIB~\citep{recon_shah2021, hiql_park2023} trains goal representations via a variational information bottleneck (VIB) within a goal-conditioned value function or policy."
- Yoneda lemma: A foundational result in category theory stating that objects can be characterized by their morphisms to/from other objects. Example: "the Yoneda lemma implies that we can identify an object through its morphisms to all other objects in the same category"
Collections
Sign up for free to add this paper to one or more collections.