Attention Sinks and Compression Valleys in LLMs are Two Sides of the Same Coin (2510.06477v1)

Abstract: Attention sinks and compression valleys have attracted significant attention as two puzzling phenomena in LLMs, but have been studied in isolation. In this work, we present a surprising connection between attention sinks and compression valleys, tracing both to the formation of massive activations in the residual stream. We prove theoretically that massive activations necessarily produce representational compression and establish bounds on the resulting entropy reduction. Through experiments across several models (410M-120B parameters), we confirm that when the beginning-of-sequence token develops extreme activation norms in the middle layers, both compression valleys and attention sinks emerge simultaneously. Targeted ablation studies validate our theoretical predictions. This unified view motivates us to propose the Mix-Compress-Refine theory of information flow, as an attempt to explain how LLMs organize their computation in depth by controlling attention and representational compression via massive activations. Specifically, we posit that Transformer-based LLMs process tokens in three distinct phases: (1) broad mixing in the early layers, (2) compressed computation with limited mixing in the middle layers, and (3) selective refinement in the late layers. Our framework helps explain why embedding tasks perform best at intermediate layers, whereas generation tasks benefit from full-depth processing, clarifying differences in task-dependent representations.

• The paper reveals that massive bos token activations cause both attention sinks and compression valleys, unifying seemingly separate phenomena.
• It introduces the Mix-Compress-Refine (MCR) theory, outlining a three-phase depth-wise computation strategy in LLMs.
• Targeted ablations and empirical analysis validate that controlling massive activations eliminates compression effects and attention sinks.

Unified Mechanisms of Attention Sinks and Compression Valleys in LLMs

Introduction

The paper "Attention Sinks and Compression Valleys in LLMs are Two Sides of the Same Coin" (2510.06477) presents a comprehensive mechanistic and theoretical analysis of two prominent phenomena in LLMs: attention sinks and compression valleys. The authors establish that both are emergent consequences of massive activations in the residual stream, particularly on the beginning-of-sequence (bos) token. This work provides a unified theoretical and empirical framework, demonstrating that these phenomena are not independent but are tightly coupled manifestations of the same underlying mechanism. The paper further introduces the Mix-Compress-Refine (MCR) theory, which characterizes the depth-wise organization of computation in LLMs.

Empirical Synchronization of Sinks and Compression

The authors empirically demonstrate that attention sinks and compression valleys emerge simultaneously across a wide range of model families and scales (410M–120B parameters). The key metrics tracked are the matrix-based entropy of the representation matrix, the bos sink rate (fraction of heads focusing on the bos token), and the bos token norm. Across all examined models, these metrics exhibit tightly synchronized transitions: the bos norm spikes by several orders of magnitude, entropy drops sharply (indicating compression), and sink rates surge to near 1.0 in the same layers.

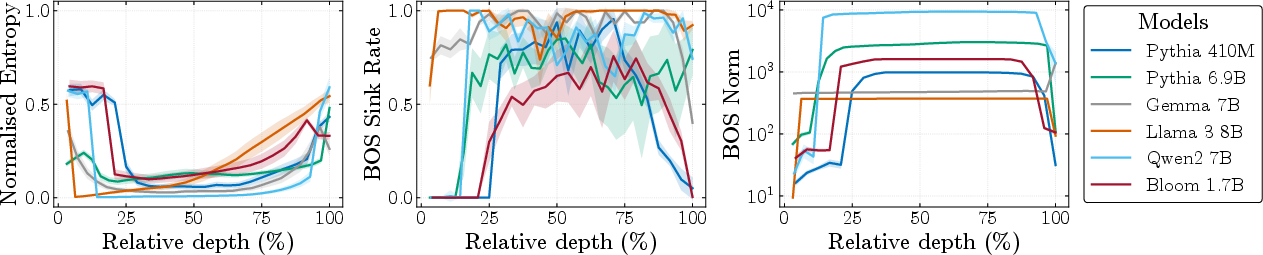
Figure 1: Attention sinks and compression valleys emerge simultaneously when bos tokens develop massive activations; all three metrics align across depth for six models.

This synchronization is robust to input variation and model scale, indicating an architectural rather than data-driven origin. The coupled emergence is also observed early in training and persists throughout, as shown by tracking these metrics across training checkpoints.

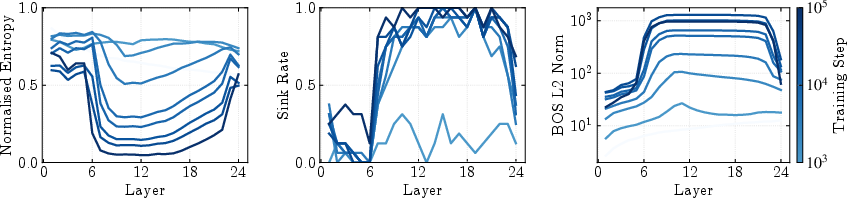
Figure 2: The coupled emergence of massive activations, compression, and sinks develops early in training and persists throughout model development.

Theoretical Analysis: Massive Activations Imply Compression

The core theoretical contribution is a set of tight lower bounds relating the norm of the bos token (massive activation) and the alignment of other token representations to the dominance of the top singular value of the representation matrix. The main result is that when the bos token norm $M$ is much larger than the sum of the norms of other tokens $R$, the representation matrix becomes nearly rank-one, and the entropy of its singular value spectrum collapses. The bounds become exact in the regime where massive activations are present, as confirmed by empirical measurements.

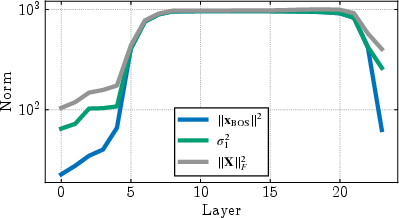
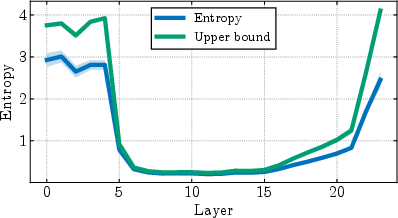
Figure 3: Theoretical bounds become exact when massive activations emerge, proving they drive compression; the first singular value and entropy upper bound match empirical values in compressed layers.

This analysis formalizes the intuition that a single high-norm token induces a dominant direction in representation space, leading to both low entropy (compression) and high anisotropy.

Causal Evidence via Targeted Ablations

To establish causality, the authors perform targeted ablations by zeroing the MLP contribution to the bos token at layers where massive activations emerge. This intervention eliminates both the entropy drop (compression) and the formation of attention sinks, while keeping the bos norm comparable to other tokens. This result holds across multiple model families, though some model-dependent exceptions are noted (e.g., in Pythia 410M, sinks can persist despite decompression).

Figure 4: Removing massive activations eliminates both compression and attention sinks, confirming causality via MLP ablation.

Mix-Compress-Refine Theory of Depth-wise Computation

Building on these findings, the paper proposes the Mix-Compress-Refine (MCR) theory, which posits that LLMs organize computation into three distinct phases:

1. Mixing (Early Layers, 0–20%): Diffuse attention patterns enable broad contextual mixing, with high mixing scores and no massive activations.
2. Compression (Middle Layers, 20–85%): The emergence of massive activations on bos induces both representational compression (low entropy) and attention sinks, halting further mixing.
3. Refinement (Late Layers, 85–100%): Norms re-equalize, compression dissipates, and attention patterns shift to sharp positional or identity heads, enabling token-specific refinements.

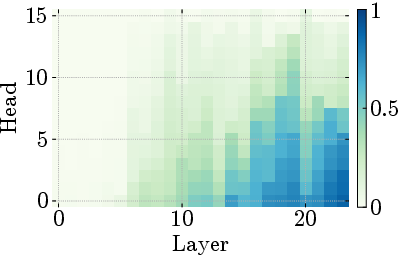
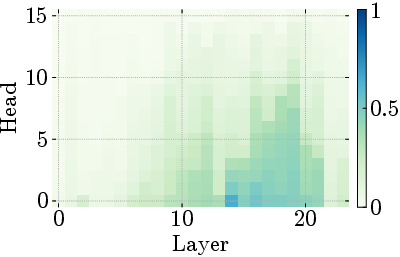
Figure 5: Middle-layer sinks adapt to input complexity while early mixing remains constant, demonstrating phase-specific computational roles.

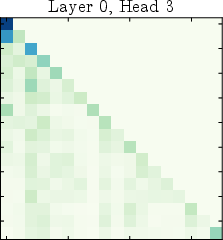
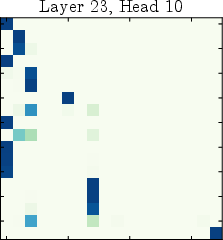
Figure 6: Attention patterns transform from diffuse mixing to sinks to positional focus across depth, illustrating the three-phase organization.

Task-Dependent Implications and Downstream Performance

A key implication of the MCR theory is the explanation of task-dependent optimal depths. Embedding tasks (e.g., classification, retrieval) achieve peak performance in the compressed middle layers, where representations are low-dimensional and linearly separable. In contrast, generation tasks (e.g., next-token prediction) require the full refinement of late layers, with performance improving monotonically through all phases.

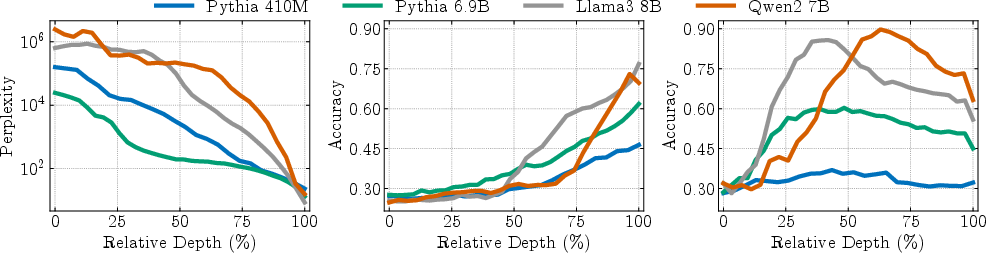
Figure 7: Embedding tasks peak during compression while generation requires full refinement, revealing distinct computational objectives and phase-specific performance.

This divergence is robust across models and datasets, and is further validated by linear probing and LogitLens/TunedLens analyses. The results clarify why different studies report different "optimal" layers for different tasks: the computational objectives are fundamentally distinct and map to different phases of the MCR organization.

Broader Model and Training Dynamics

The paper extends its analysis to a broad set of models, including very large models (70B–120B), and tracks the emergence of the phenomena across training checkpoints. The observed synchronization and phase transitions are universal across architectures, though some models (e.g., Gemma 7B) achieve norm disparity via different mechanisms (e.g., decreasing non-bos norms rather than increasing bos norm).

Limitations and Future Directions

The analysis is focused on decoder-only Transformers with explicit bos tokens and may not generalize to architectures with alternative positional encodings or attention sparsity patterns. The theoretical results assume a single massive activation, though the extension to multiple massive activations is discussed. Some model-dependent exceptions in the causal ablation results suggest further investigation is warranted.

Conclusion

This work provides a unified mechanistic and theoretical account of attention sinks and compression valleys in LLMs, demonstrating that both are consequences of massive activations in the residual stream. The Mix-Compress-Refine theory offers a principled framework for understanding depth-wise computation in Transformers, with direct implications for model analysis, interpretability, and efficient deployment. The phase-specific organization explains the divergent optimal depths for embedding and generation tasks, and suggests that phase-aware early exiting and targeted interventions on massive activations could be promising directions for future research and model design.