Beyond Regularization: Inherently Sparse Principal Component Analysis

Abstract: Sparse principal component analysis (sparse PCA) is a widely used technique for dimensionality reduction in multivariate analysis, addressing two key limitations of standard PCA. First, sparse PCA can be implemented in high-dimensional low sample size settings, such as genetic microarrays. Second, it improves interpretability as components are regularized to zero. However, over-regularization of sparse singular vectors can cause them to deviate greatly from the population singular vectors, potentially misrepresenting the data structure. Additionally, sparse singular vectors are often not orthogonal, resulting in shared information between components, which complicates the calculation of variance explained. To address these challenges, we propose a methodology for sparse PCA that reflects the inherent structure of the data matrix. Specifically, we identify uncorrelated submatrices of the data matrix, meaning that the covariance matrix exhibits a sparse block diagonal structure. Such sparse matrices commonly occur in high-dimensional settings. The singular vectors of such a data matrix are inherently sparse, which improves interpretability while capturing the underlying data structure. Furthermore, these singular vectors are orthogonal by construction, ensuring that they do not share information. We demonstrate the effectiveness of our method through simulations and provide real data applications. Supplementary materials for this article are available online.

• The paper proposes IS-PCA, which inherently aligns sparse singular vectors with natural block diagonal covariance structures.
• It overcomes over-regularization and non-orthogonality issues in traditional sparse PCA, ensuring accurate variance estimation.
• Validation on gene expression datasets shows improved separation of tumor types and enhanced interpretability of principal components.

Inherently Sparse Principal Component Analysis

Introduction

The paper "Beyond Regularization: Inherently Sparse Principal Component Analysis" addresses the challenges associated with traditional PCA in high-dimensional, low-sample size (HDLSS) data environments. This study puts forth a method to refine sparse PCA, enhancing interpretability while preserving the data's inherent structure. The authors present a new methodology, inherently sparse PCA (IS-PCA), which aligns singular vectors with the sparse covariance structures observed often in gene expression matrices and other high-dimensional datasets.

Methodology

Sparse Principal Component Analysis Challenges

Sparse PCA is designed to overcome the limitations of standard PCA, especially in settings where high dimensionality and low sample sizes prevail, such as genetic microarray analyses. Traditional PCA computes principal components as linear combinations of all original variables, often resulting in non-zero singular vector components across inputs—hindering interpretability. Sparse PCA improves upon this by zeroing out certain component weights, thus clarifying interpretation. However, the paper identifies critical limitations in sparse PCA:

• Over-regularization: Excessive regularization leads sparse singular vectors to deviate from population singular vectors, miscalculating singular values and explained variance.
• Non-orthogonal Vectors: Regularization can yield non-orthogonal vectors, leading to shared information between components and complicating variance calculations.

Proposed Methodology: IS-PCA

The authors propose a novel approach, IS-PCA, which inherently mirrors the sparse block diagonal structure of the covariance matrix. This structure, prevalent in high-dimensional data, makes singular vectors naturally sparse and orthogonal. The authors leverage the block diagonal configuration to ensure orthogonality and non-overlapping contribution among singular vectors. The method involves:

1. Detection of sparse block submatrices within the data matrix.
2. Construction of sparse PC loadings from these submatrices, preserving orthogonal singular vectors by padding them with zeros.

Essentially, IS-PCA maintains the structural integrity of singular vectors, aligning them rigorously with inherent covariance matrix traits without over-regularizing.

Simulation and Real Data Validation

Simulations

The simulation study highlights IS-PCA's enhanced singular vector estimation compared to CDM and PMD methods. The simulation maintained an HDLSS framework and benchmarked various estimation approaches, demonstrating IS-PCA's accuracy in detecting block structures and estimating explained variances. The results underscore IS-PCA's role in improving singular vector and eigenvalue accuracy, especially evident in "Oracle Block IS-PCA" where the known block structure is used.

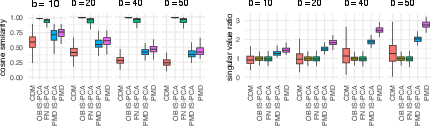
Figure 1: Simulation results for CDM (red), OB IS-PCA (yellow), FN IS-PCA (green), PMD IS-PCA (blue), and PMD (pink) for the cosine similarity $| \bm{v}^T \tilde{\bm{v}|$.

Real Data Applications

Real data applications in gene expression profiles for both prostate tumors and lymphoma malignancies further validate IS-PCA's practical relevance. By analyzing the prostate tumor dataset, IS-PCA efficiently identified a submatrix of 219 variables, capturing significant variance and facilitating tumor type separation.

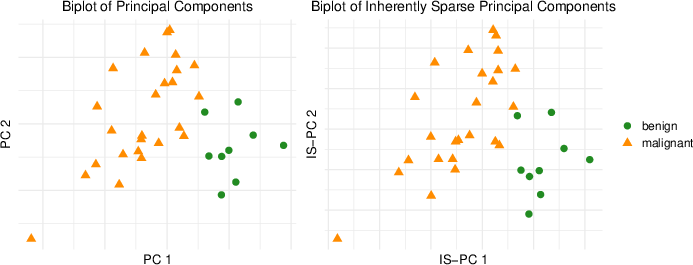
Figure 2: Biplots for a gene expression data matrix comprising 9 benign (noncancerous) prostate tumors (green, bullet) and 25 malignant (cancerous) observations (orange, blacktriangle).

Similarly, IS-PCA's application on a lymphoma dataset yielded improved separation between malignant types, notably identifying a sparse singular vector that enhanced distinction between follicular lymphoma and chronic lymphocytic leukemia.

Figure 3: The first PC (left) and fifth sparse PC (right) for the prostate tumors gene expression data set, showing distinction improvement between tumor types.

Discussion

IS-PCA represents a significant advancement in PCA methodologies, especially in high-dimensional scenarios where traditional approaches fall short. It circumvents the pitfalls of over-regularization by aligning sparse singular vectors with the genuine structural layout of data matrices. This improves not only interpretability but also provides orthogonality, facilitating clearer variance computation.

Future research could explore the interrelationship between principal submatrices and principal variables. Leveraging efficient submatrix segmentation could refine methods for identifying key principal variables—the core contributors to variance explanation in these complex datasets.

Conclusion

The research presented in the paper enriches the PCA toolbox with a robust method suited for high-dimensional environments, relying less on arbitrary regularization and more on elegant structural alignment. IS-PCA has demonstrated practical benefits in gene expression analysis and is poised for broader applications in data science domains where dimensionality reduction and clear interpretability remain challenging.