Distributed Connectivity Maintenance and Recovery for Quadrotor Motion Planning (2510.03504v1)

Abstract: Maintaining connectivity is crucial in many multi-robot applications, yet fragile to obstacles and visual occlusions. We present a real-time distributed framework for multi-robot navigation certified by high-order control barrier functions (HOCBFs) that controls inter-robot proximity to maintain connectivity while avoiding collisions. We incorporate control Lyapunov functions to enable connectivity recovery from initial disconnected configurations and temporary losses, providing robust connectivity during navigation in obstacle-rich environments. Our trajectory generation framework concurrently produces planning and control through a Bezier-parameterized trajectory, which naturally provides smooth curves with arbitrary degree of derivatives. The main contribution is the unified MPC-CLF-CBF framework, a continuous-time trajectory generation and control method for connectivity maintenance and recovery of multi-robot systems. We validate the framework through extensive simulations and a physical experiment with 4 Crazyflie nano-quadrotors.

• The paper presents a unified framework integrating MPC, CLF, and CBF for predictive quadrotor motion planning in cluttered environments.
• It employs B-Spline trajectories and quadratic programming to ensure smooth paths, connectivity maintenance, and safe obstacle avoidance.
• Simulation and physical experiments demonstrate improved success rates, reduced makespan, and effective connectivity recovery compared to baseline approaches.

Distributed Connectivity Maintenance and Recovery for Quadrotor Motion Planning

This essay discusses the paper titled "Distributed Connectivity Maintenance and Recovery for Quadrotor Motion Planning" which presents a unified framework incorporating Model Predictive Control (MPC), Control Lyapunov Functions (CLF), and Control Barrier Functions (CBF) for robust quadrotor motion planning in cluttered environments. This framework aims to maintain and recover connectivity within multi-robot systems, ensuring safe and efficient navigation.

Introduction to Connectivity Maintenance

Connectivity maintenance is crucial in multi-robot systems to enable effective coordination and information exchange. These systems can be fragile due to obstacles and occlusions that prevent robots from staying within communication range. The paper proposes a hybrid approach combining local and global strategies to adaptively maintain connectivity while allowing reconfiguration.

Figure 1: Long exposure of 4 quadrotors navigating a cluttered environment with 6 obstacles. All quadrotors are connected at the beginning, and the team is forced to disconnect into 2 subgroups to avoid obstacles. Eventually, all robots reconnect and reach their goals.

Control Barrier Functions and High-Order Extensions

Control Barrier Functions (CBFs) are used to ensure safety in nonlinear control systems by making sets forward invariant. The introduction of High-Order Control Barrier Functions (HOCBFs) extends this concept to systems with high relative degrees, providing a mechanism to enforce constraints in higher-order dynamics.

The CBFs are complemented by CLFs which drive the system towards desired goals, ensuring connectivity recovery after disconnections. This is essential for maintaining connectivity in environments where temporary losses are inevitable due to obstacles.

B-Spline Trajectory Generation

The framework uses B-Spline curves for trajectory generation, providing smooth paths with high-order derivatives, suitable for agile systems like quadrotors. B-Splines inherently offer the smoothness required for real-time trajectory optimization and are implemented in a piecewise fashion to handle extended planning horizons efficiently.

Problem Formulation and Framework Implementation

The problem is formulated by considering a team of robots navigating a 2D space, articulated with double integrator dynamics. Connectivity is quantified with the Fiedler eigenvalue (algebraic connectivity) of the graph representing the robot network. The core novelty lies in the MPC-CLF-CBF integration, providing predictive and reactive control. Each robot solves a quadratic program at each timestep to satisfy safety, connectivity, and goal-reaching requirements concurrently.

Figures throughout the paper illustrate model behaviors under various conditions — notably, situations involving dynamic reconnection after temporary disconnections due to environmental constraints.

Simulation Experiments and Results

Simulation results validate the proposed approach in scenarios featuring obstacle avoidance, disconnection recovery, and performance scalability. The metrics — success rate, makespan, and percentage connected — highlight the framework's efficacy relative to baseline approaches.

Figure 2: CLF-CBF baseline

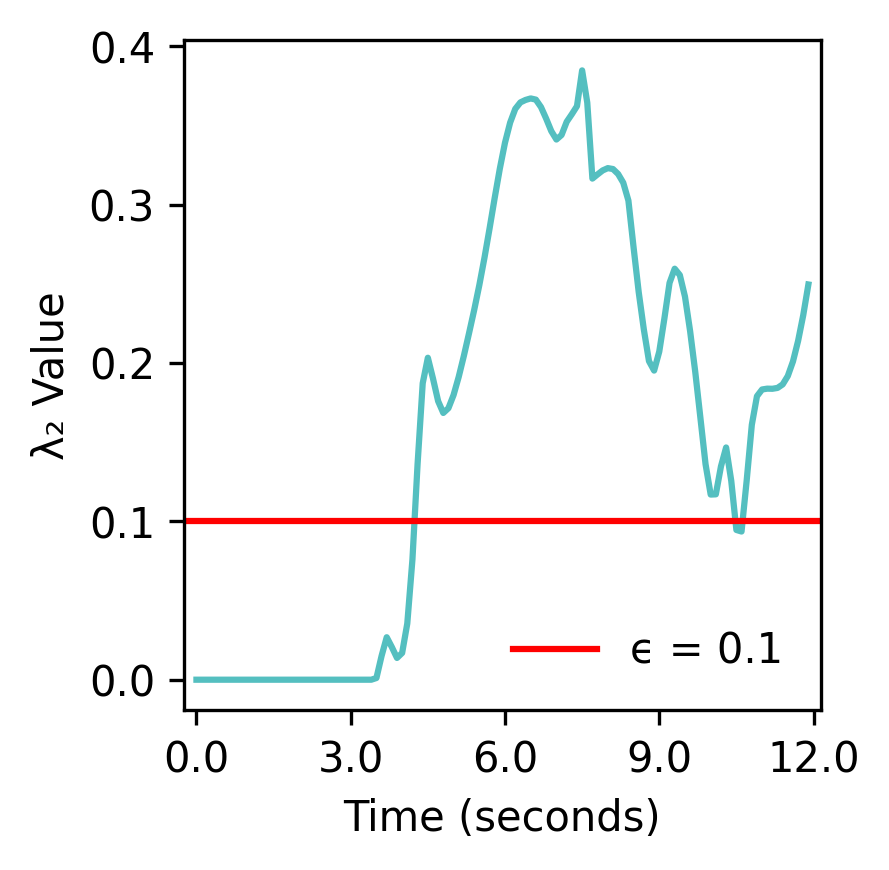
Figure 3: Algebraic connectivity throughout the recovery

Comparative Analysis

Comparative analysis demonstrates that the proposed MPC-CLF-CBF framework offers substantial improvements over CLF-CBF and MPC-CBF baselines. It exhibits higher success rates, reduced makespan, and improved connectivity maintenance in both obstacle-rich and obstacle-free scenarios.

Physical Experiments

The framework's practical applicability is validated with experiments involving Crazyflie nano-quadrotors. These experiments demonstrate successful real-time navigation in cluttered environments, confirming the framework's robustness and potential for real-world application.

Conclusion

The research introduces a robust trajectory planning framework for multi-robot connectivity maintenance and recovery. Results underscore its ability to navigate complex environments while maintaining system connectivity, paving the way for future applications in diverse robotic tasks such as formation control and exploration.

The framework offers promising directions for extension to 3D environments and heterogeneous robot teams, necessitating further validation on more complex robotic models and dynamic setups.