Universal Beta Splatting (2510.03312v1)

Abstract: We introduce Universal Beta Splatting (UBS), a unified framework that generalizes 3D Gaussian Splatting to N-dimensional anisotropic Beta kernels for explicit radiance field rendering. Unlike fixed Gaussian primitives, Beta kernels enable controllable dependency modeling across spatial, angular, and temporal dimensions within a single representation. Our unified approach captures complex light transport effects, handles anisotropic view-dependent appearance, and models scene dynamics without requiring auxiliary networks or specific color encodings. UBS maintains backward compatibility by approximating to Gaussian Splatting as a special case, guaranteeing plug-in usability and lower performance bounds. The learned Beta parameters naturally decompose scene properties into interpretable without explicit supervision: spatial (surface vs. texture), angular (diffuse vs. specular), and temporal (static vs. dynamic). Our CUDA-accelerated implementation achieves real-time rendering while consistently outperforming existing methods across static, view-dependent, and dynamic benchmarks, establishing Beta kernels as a scalable universal primitive for radiance field rendering. Our project website is available at https://rongliu-leo.github.io/universal-beta-splatting/.

• The paper introduces an N-D Beta kernel framework that overcomes Gaussian primitive limitations by enabling independent modeling of spatial, angular, and temporal properties.
• It employs spatial-orthogonal Cholesky parameterization and Beta-modulated conditioning to achieve up to +8.27 dB PSNR improvement on static scenes and notable gains on dynamic scenes.
• The method is backward compatible with Gaussian splatting while reducing per-primitive parameters by 73% and cutting training time by up to 69.2%.

Universal Beta Splatting: A Unified Framework for N-Dimensional Explicit Radiance Field Rendering

Introduction

Universal Beta Splatting (UBS) introduces a unified, explicit radiance field representation that generalizes 3D Gaussian Splatting (3DGS) to $N$-dimensional anisotropic Beta kernels. The framework is designed to overcome the representational limitations of fixed Gaussian primitives, which are inherently constrained by their symmetric bell-shaped profiles and coupled dimensional dependencies. UBS enables per-dimension shape control, allowing for independent modeling of spatial geometry, angular appearance, and temporal dynamics within a single primitive. This approach eliminates the need for auxiliary networks or color encodings, streamlining both the parameterization and computational pipeline.

Figure 1: UBS achieves superior rendering of reflective/specular materials in static scenes and maintains high fidelity in dynamic volumetric scenes compared to 3DGS and 4DGS.

Methodology

N-Dimensional Beta Kernel Formulation

UBS models the radiance field using $N$-dimensional Beta kernels parameterized by mean $\bm{\mu} \in \mathbb{R}^N$, covariance $\bm{\Sigma} \in \mathbb{R}^{N \times N}$, and per-dimension Beta shape parameters $\bm{b} \in \mathbb{R}^{N-2}$. The kernel density is given by:

$$\sigma(\bm{x}, \bm{q}) = B(\bm{x}, \bm{q};\,\bm{\mu},\,\bm{\Sigma},\,\bm{b})$$

where $\bm{x}$ are spatial coordinates and $\bm{q}$ encodes additional dimensions (view, time, etc.). The Beta exponent $\beta_i = 4\exp(b_i)$ allows each dimension to adopt a flat, Gaussian-like, or peaked profile, enabling efficient modeling of diverse scene properties.

Spatial-Orthogonal Cholesky Parameterization

To ensure geometric consistency and positive semi-definiteness of the covariance matrix, UBS employs a spatial-orthogonal Cholesky parameterization. The spatial subspace is rotated using a skew-symmetric matrix with a first-order Taylor approximation, while cross-dimensional correlations are handled via Cholesky factors. This hybrid approach preserves explicit 3D geometric structure and enables flexible modeling of view and temporal dependencies.

Beta-Modulated Conditional Slicing

Rendering at a query condition $\bm{q}$ involves conditioning the $N$-dimensional kernel to obtain a 3D spatial representation. Beta modulation is applied to the conditional mean and covariance, allowing dimension-specific anisotropy. Opacity is factorized in product form, providing independent control over each non-spatial dimension. The final density is:

$$\sigma(\bm{x}, \bm{q}) = B(\bm{x};\, \bm{\mu}_{x\mid q},\, \bm{\Sigma}_{x\mid q},\, b_x) \cdot o(\bm{q})$$

Universal Compatibility and Interpretability

UBS is backward compatible: setting all Beta parameters to zero recovers Gaussian splatting (3DGS, 6DGS, 7DGS). The learned Beta parameters naturally decompose scene properties without supervision, distinguishing geometry, appearance, and motion components.

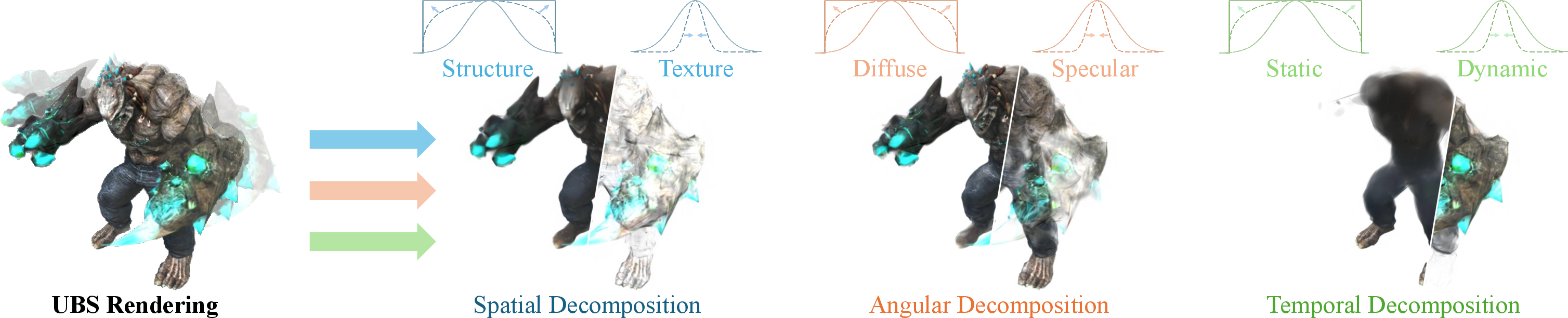
Figure 2: Learned Beta parameters provide interpretable decomposition across spatial, angular, and temporal dimensions.

Optimization and Implementation

UBS leverages MCMC-based primitive management, reconstruction and regularization losses, and spatial noise injection for stable optimization. The CUDA-accelerated implementation supports real-time rendering and is compatible with existing splatting frameworks.

Experimental Results

Static Scene Benchmarks

UBS-6D demonstrates consistent improvements over 3DGS and 6DGS across NeRF Synthetic, Mip-NeRF 360, and 6DGS-PBR datasets. Notably, UBS-6D achieves up to +8.27 dB PSNR improvement on volumetric scenes and substantial gains on view-dependent effects.

Figure 3: Qualitative comparison of UBS with baseline methods for static and dynamic scenes.

Dynamic Scene Benchmarks

UBS-7D outperforms 4DGS and 7DGS on dynamic datasets (7DGS-PBR, D-NeRF), with +2.78 dB PSNR improvement on cardiac motion and volumetric dynamics. UBS achieves these results with a 73% reduction in per-primitive parameters compared to 4DGS, due to the elimination of auxiliary color encodings.

Computational Efficiency

UBS achieves significant training time reductions (up to 69.2% on Mip-NeRF 360) and maintains real-time rendering performance. The streamlined primitive design and fused CUDA kernels contribute to these efficiency gains.

Ablation Studies

Ablations confirm the necessity of spatial-orthogonal parameterization, Beta-modulated conditioning, and product-form opacity. Disabling any component results in notable drops in reconstruction quality, especially for dynamic and volumetric scenes.

Theoretical Analysis

Limitations of Gaussian Kernels

Gaussian kernels enforce symmetric, coupled dimensional dependencies, preventing independent control of spatial, angular, and temporal properties. This results in inefficient representations for complex scenes.

Properties of Beta Kernels

Beta kernels provide per-dimension shape adaptivity, enabling flat, Gaussian-like, or peaked profiles as needed. The product form allows independent control, and backward compatibility ensures seamless integration with existing methods.

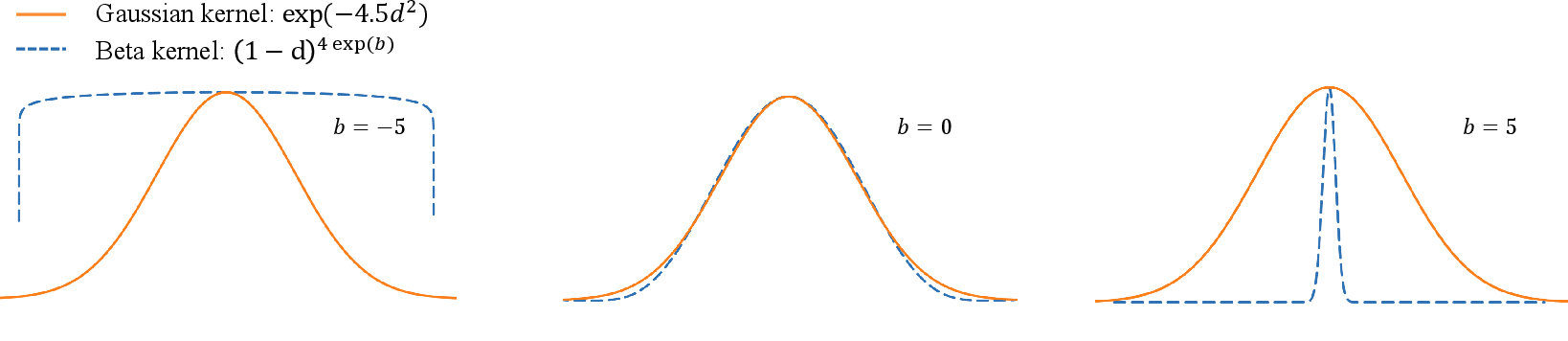
Figure 4: Adaptive Beta kernels enable dimension-specific control, spanning flat to highly peaked profiles.

Implications and Future Directions

UBS establishes Beta kernels as a scalable, universal primitive for explicit radiance field rendering. The framework's parameter efficiency and interpretability open avenues for large-scale scene modeling, real-time dynamic rendering, and applications in relighting and motion analysis. Future work may extend UBS to additional modalities (e.g., lighting, material properties), integrate with advanced acceleration techniques, and explore its utility in semantic and feature-based scene understanding.

Conclusion

Universal Beta Splatting generalizes explicit radiance field rendering to $N$-dimensional anisotropic Beta kernels, enabling independent modeling of spatial, angular, and temporal properties. The framework achieves state-of-the-art reconstruction quality, substantial parameter and computational efficiency, and interpretable scene decomposition. UBS provides a practical, extensible foundation for real-time photorealistic rendering and advanced scene analysis.