Measurement-Guided Consistency Model Sampling for Inverse Problems (2510.02208v1)

Abstract: Diffusion models have become powerful generative priors for solving inverse imaging problems, but their reliance on slow multi-step sampling limits practical deployment. Consistency models address this bottleneck by enabling high-quality generation in a single or only a few steps, yet their direct adaptation to inverse problems is underexplored. In this paper, we present a modified consistency sampling approach tailored for inverse problem reconstruction: the sampler's stochasticity is guided by a measurement-consistency mechanism tied to the measurement operator, which enforces fidelity to the acquired measurements while retaining the efficiency of consistency-based generation. Experiments on Fashion-MNIST and LSUN Bedroom datasets demonstrate consistent improvements in perceptual and pixel-level metrics, including Fr\'echet Inception Distance, Kernel Inception Distance, peak signal-to-noise ratio, and structural similarity index measure, compared to baseline consistency sampling, yielding competitive or superior reconstructions with only a handful of steps.

• The paper introduces Inverse-aDDIM, which integrates measurement residue-based variance compensation into consistency model sampling.
• It achieves high-quality reconstructions on tasks like super-resolution, inpainting, and deblurring with as few as two sampling steps.
• Experimental evaluations demonstrate improved perceptual metrics (KID, FID) and competitive pixel-level scores (PSNR, SSIM) across datasets.

Measurement-Guided Consistency Model Sampling for Inverse Problems

Introduction and Motivation

This paper addresses the challenge of efficiently solving inverse imaging problems using diffusion-based generative models. While diffusion models have demonstrated strong performance as priors for ill-posed inverse problems, their practical deployment is hindered by the need for hundreds of iterative sampling steps. Consistency models (CMs) offer a solution by enabling high-quality generation in a single or a few steps, but their direct application to inverse problems is nontrivial due to the need to enforce measurement fidelity. The authors propose a deterministic sampling strategy, Inverse-aDDIM, that integrates measurement consistency into the CM sampling process, thereby improving both efficiency and reconstruction quality for a range of inverse problems.

Background: Diffusion and Consistency Models in Inverse Problems

Inverse problems are formulated as recovering an unknown signal $\boldsymbol{x}$ from degraded measurements $\boldsymbol{y} = A(\boldsymbol{x}) + n$, where $A$ is a degradation operator and $n$ is noise. The Bayesian approach seeks the MAP estimate by maximizing the posterior $$p(\boldsymbol{x}|\boldsymbol{y}) \propto p(\boldsymbol{y}|\boldsymbol{x})p(\boldsymbol{x})$$, where $p(\boldsymbol{x})$ is the prior.

Diffusion models learn $p(\boldsymbol{x})$ by reversing a noising process, but require many steps for sampling. Denoising Diffusion Restoration Models (DDRM) adapt diffusion models for inverse problems by iteratively sampling from the posterior, but remain computationally expensive. Consistency models (CMs) address this by learning a mapping from noisy latents to clean samples, enabling few-step or even single-step generation. However, enforcing measurement consistency within CM sampling remains an open problem.

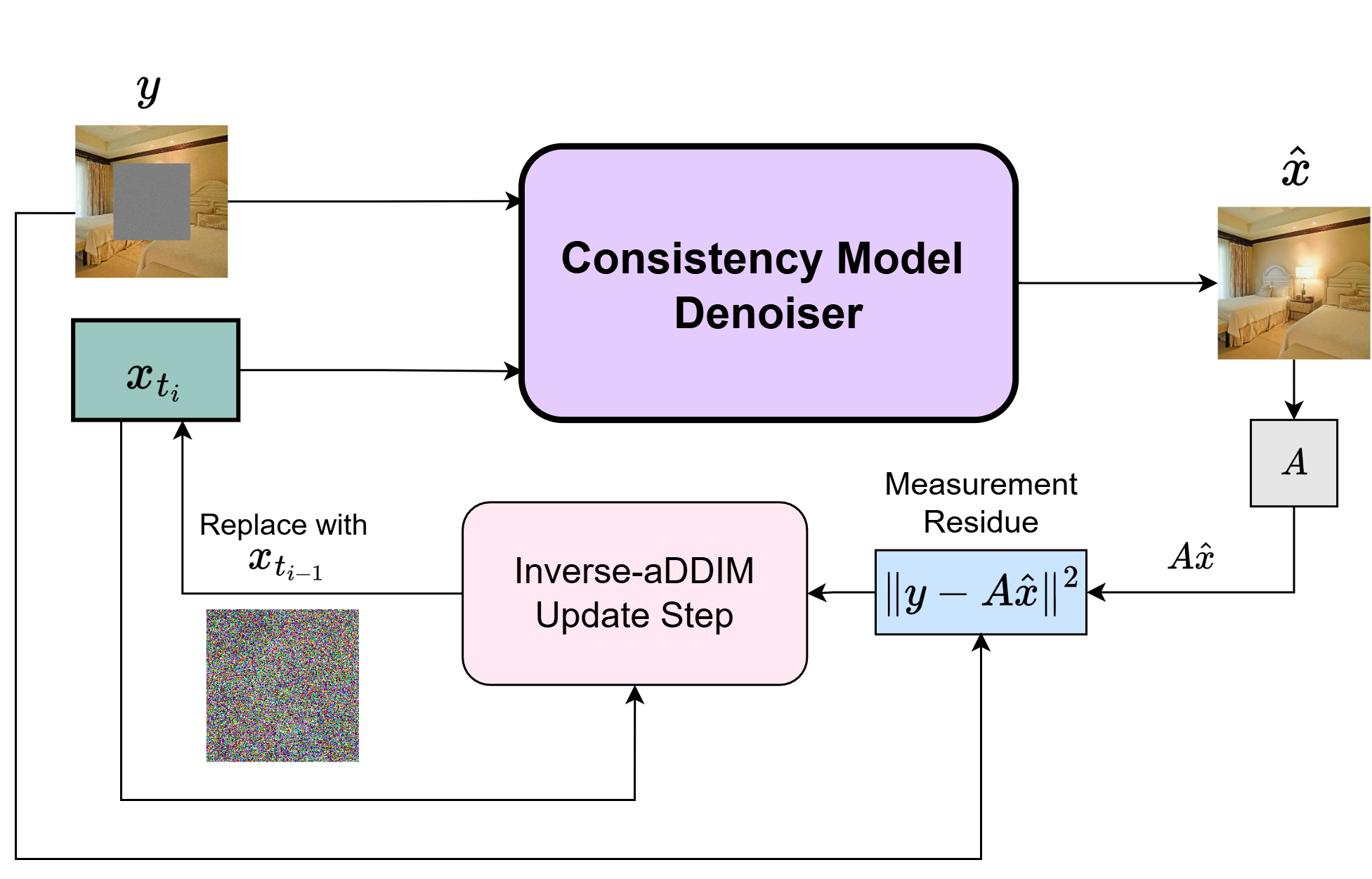
Inverse-aDDIM: Measurement-Consistent Consistency Model Sampling

The core contribution is the Inverse-aDDIM algorithm, which adapts the aDDIM sampler for CMs to inverse problems by incorporating a measurement-driven variance term. In standard aDDIM, the variance term is estimated using a teacher signal, which is unavailable in inverse problems. The authors propose replacing this with the measurement residue $\|\boldsymbol{y} - A\hat{\boldsymbol{x}}\|^2$, directly reflecting the fidelity of the reconstruction to the observed measurements.

The Inverse-aDDIM update is as follows:

• At each step, the CM predicts a clean sample $$\hat{\boldsymbol{x}} = f_\theta(\boldsymbol{x}_t, \boldsymbol{y}, t)$$.
• The update to the next latent $\boldsymbol{x}_s$ is computed using a variance term proportional to the measurement residue, modulated by a hyperparameter $\gamma$.
• This approach adaptively injects stochasticity when the reconstruction deviates from the measurements and becomes deterministic as measurement fidelity improves.

  Figure 1: Illustration of the proposed Inverse-aDDIM framework, where measurement consistency is enforced using the measurement residue.

Theoretical justification is provided by showing that, for linear $A$, the expected measurement residue upper-bounds the original variance term, ensuring that the variance compensation property of aDDIM is preserved.

Experimental Evaluation

Datasets and Tasks

Experiments are conducted on the LSUN Bedroom (256×256) and Fashion-MNIST (28×28) datasets. The authors evaluate on three canonical inverse problems—super-resolution, inpainting, and deblurring—plus a nonlinear deblurring task for LSUN Bedroom. For LSUN, a ControlNet-based CoSIGN model is used; for Fashion-MNIST, a CM with an auxiliary network is employed.

Quantitative Results

On Fashion-MNIST, Inverse-aDDIM consistently outperforms baseline CM sampling across all metrics (PSNR, SSIM, KID, FID). On LSUN Bedroom, Inverse-aDDIM achieves lower KID and FID (better perceptual quality) while maintaining competitive PSNR and SSIM. Notably, the method achieves these results with only two sampling steps, demonstrating significant computational efficiency.

Qualitative Results

Visual comparisons show that Inverse-aDDIM produces reconstructions with improved perceptual quality and measurement fidelity across all tasks.

Figure 2: Visual comparison on four inverse problems on the LSUN Bedroom dataset: super-resolution (top row), deblurring (second row), inpainting (third row), and nonlinear deblurring (bottom row).

Figure 3: Visual comparison on three inverse problems: super-resolution (top), deblurring (middle), and inpainting (bottom) on the Fashion-MNIST dataset.

Implementation Considerations

• Integration: Inverse-aDDIM can be integrated into any CM-based inverse problem solver without retraining the backbone, requiring only access to the measurement operator $A$ and the measurement $\boldsymbol{y}$.
• Hyperparameters: The variance compensation hyperparameter $\gamma$ must be tuned for each task to balance measurement fidelity and sample diversity.
• Computational Efficiency: The method achieves strong results with as few as two sampling steps, making it suitable for real-time or large-scale applications.
• Limitations: Slight reductions in pixel-level metrics (PSNR, SSIM) may occur due to the generation of perceptually plausible but pixel-wise different details, especially on complex datasets.

Implications and Future Directions

The proposed measurement-guided sampling strategy demonstrates that CMs can be effectively adapted to inverse problems with minimal computational overhead and without sacrificing reconstruction quality. This approach is particularly relevant for applications requiring fast inference, such as medical imaging or remote sensing. The method's generality suggests applicability to a wide range of linear and nonlinear inverse problems.

Future work may explore:

• Extension to more complex, non-linear, or non-Gaussian measurement operators.
• Task-specific adaptation of the measurement residue term.
• Joint training of the CM and measurement-guided sampler for further gains.
• Application to high-dimensional or multi-modal inverse problems.

Conclusion

This work introduces Inverse-aDDIM, a measurement-aware sampling algorithm for consistency models that enforces measurement fidelity via variance compensation using the measurement residue. The method achieves efficient, high-quality reconstructions across diverse inverse problems and datasets, with strong perceptual and pixel-level performance in only a few sampling steps. The approach provides a principled and practical solution for integrating measurement consistency into fast generative inverse problem solvers, with broad implications for future research and deployment in computational imaging.