Rethinking KL Regularization in RLHF: From Value Estimation to Gradient Optimization (2510.01555v1)
Abstract: Reinforcement Learning from Human Feedback (RLHF) leverages a Kullback-Leibler (KL) divergence loss to stabilize training and prevent overfitting. However, in methods such as GRPO, its implementation may be guided by principles from numerical value estimation-a practice that overlooks the term's functional role as an optimization loss. To analyze this issue, we establish a unified framework that connects two seemingly distinct implementation styles: using the mathematical term $k_n$ as a detached coefficient for the policy's score function ('$k_n$ in reward') or as a direct loss function through which gradients are propagated ('$k_n$ as loss'). We show that the latter can always be analyzed via an equivalent gradient coefficient in the former, unifying the two perspectives. Through this framework, we prove that the conventional '$k_1$ in reward' (like in PPO) is the principled loss for Reverse KL (RKL) regularization. We further establish a key finding: under on-policy conditions, the '$k_2$ as loss' formulation is, in fact, gradient-equivalent to '$k_1$ in reward'. This equivalence, first proven in our work, identifies both as the theoretically sound implementations of the RKL objective. In contrast, we show that the recently adopted '$k_3$ as loss' (like in GRPO) is merely a first-order, biased approximation of the principled loss. Furthermore, we argue that common off-policy implementations of '$k_n$ as loss' methods are biased due to neglected importance sampling, and we propose a principled correction. Our findings provide a comprehensive, gradient-based rationale for choosing and correctly implementing KL regularization, paving the way for more robust and effective RLHF systems.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper looks at how we train LLMs (like chatbots) using feedback from humans, a process called RLHF. During RLHF, we add a penalty called “KL regularization” to stop the model from drifting too far away from a safer starting version (the supervised fine-tuned model). The authors argue that people often use this penalty the wrong way: they focus on measuring the size of the penalty (a number) instead of how it changes the direction of learning (the gradient). The paper fixes this by showing which KL penalty forms actually give the right learning signal and which ones don’t.
Key questions the paper asks
- When we add the KL penalty in RLHF, what is the correct way to make it influence the model’s learning direction?
- Are the different popular ways of implementing the KL penalty actually equivalent—or are some of them biased or ineffective?
- Why do some modern methods (like GRPO) behave unstably, and how can we correct them?
How the authors approached it
Think of training a model like teaching a student:
- The student is the current model.
- The “reference” is a trusted notebook with safe, good answers (the model before RL).
- Human feedback tells the student which answers are better.
- The KL penalty says: “Don’t wander too far from the notebook while improving.”
The authors compare two main ways people plug the KL penalty into training:
1) “In reward” style: treat the KL term as a fixed weight that multiplies the usual learning signal. In everyday terms, this is like adjusting how strong your “don’t drift too far from the notebook” voice is, without letting that voice change itself during the update.
2) “As loss” style: make the KL term a separate loss that directly pushes the model during training. Here, the KL term itself sends a learning “nudge,” not just a fixed weight.
They use math to paper the gradients—the directions the model gets pushed in each step—and prove when these styles are truly equivalent and when they are not. They also run experiments on math reasoning tasks to check their claims.
Helpful analogies for key terms:
- Gradient: the “direction to move” to improve the model, like “turn a little left” in a maze.
- On-policy: the student learns from answers it just produced itself.
- Off-policy: the student learns from old or different answers (not from its current behavior).
- Importance sampling: a fairness correction when learning from off-policy data, like adjusting points because some questions were much more common in the old homework than in today’s practice.
Main findings
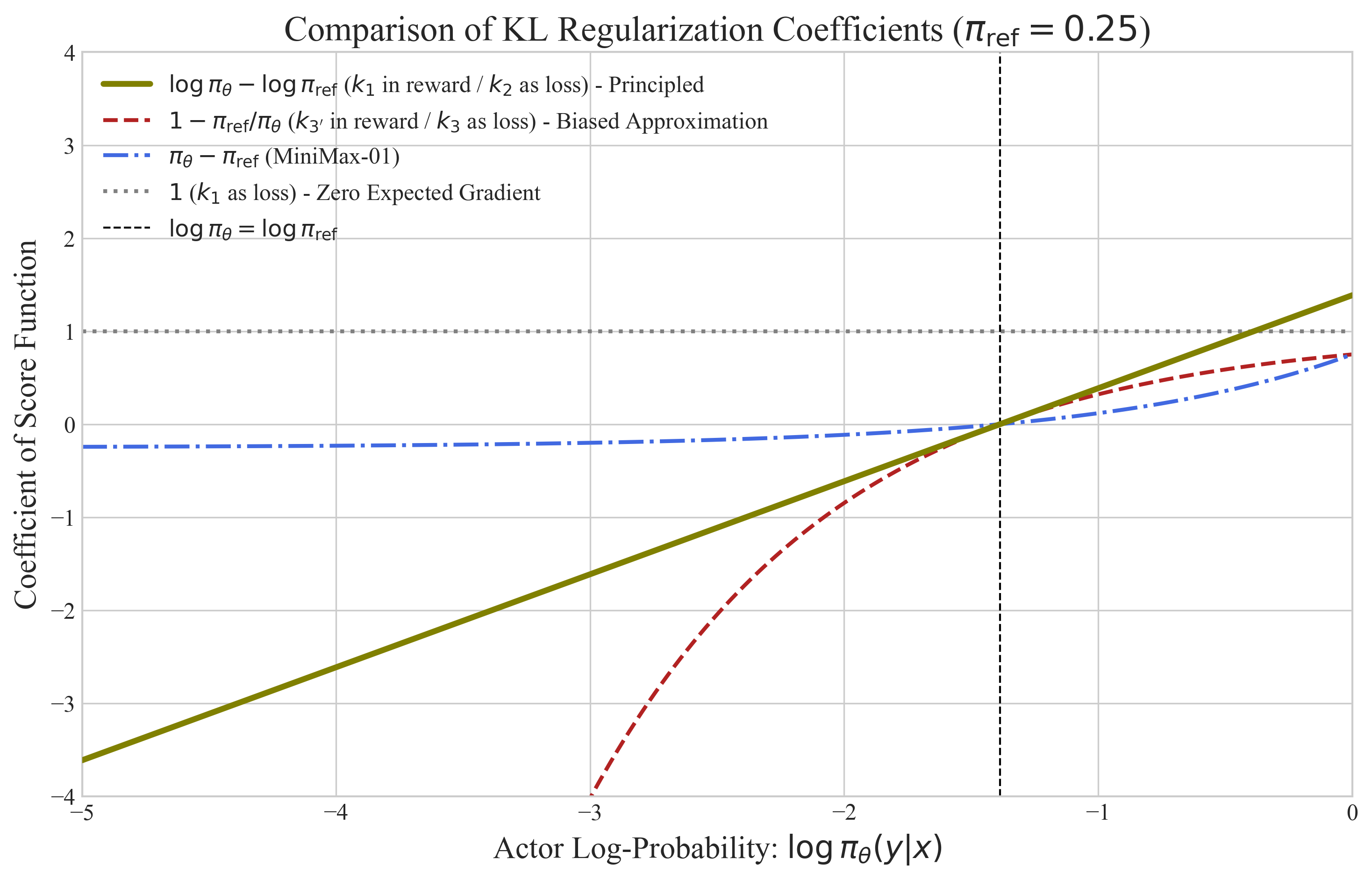
- The popular “k1 as loss” is misleading. Even though “k1” can estimate the size of the KL penalty, using it directly as a loss gives almost no regularizing push. In simple terms: it measures a difference but doesn’t push the model in the right way. Its average gradient is zero, so it adds noise without helpful guidance.
- Two implementations are principled and equivalent (on-policy):
- “k1 in reward”: treat the log-ratio between the current model and the reference as a fixed weight multiplying the usual learning signal.
- “k2 as loss”: use the squared log-ratio as a direct loss and let its gradient flow.
- They prove these produce the same effective gradient when training on the model’s own samples. That means both are solid choices and you can pick either.
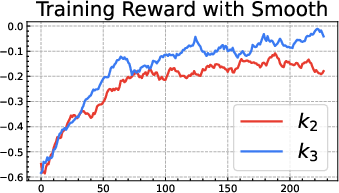
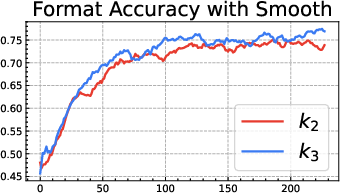
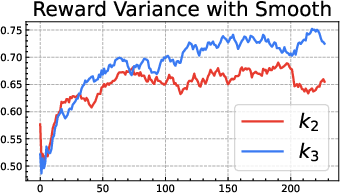
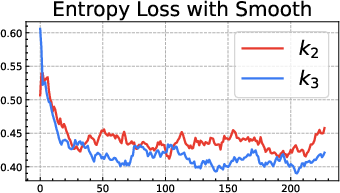
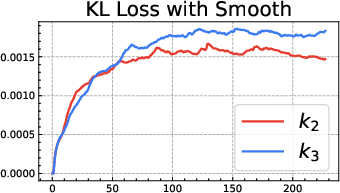
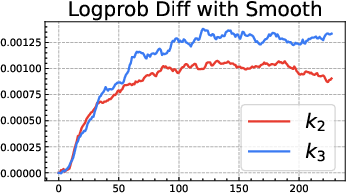
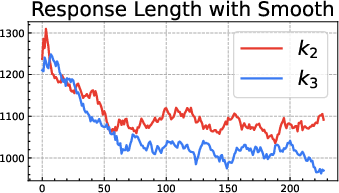
- The popular “k3 as loss” (used in GRPO) is only a first-order approximation. It’s like using a quick shortcut for “stay close to the notebook” that works well only when you’re already very close. Far away, it can be too weak in some places and too strong in others, leading to bias and instability:
- When the current model is much more confident than the reference on some answers, the k3 penalty becomes too soft, letting the model drift more.
- When the current model is much less confident, the k3 penalty can blow up and push too hard, causing instability.
- Off-policy implementations of “as loss” are often biased. If you use past data or other sources (off-policy) and don’t apply importance sampling and PPO-style clipping to the KL term itself, you systematically skew the learning direction. The paper explains how to correct this.
Why these results matter
Getting the KL penalty right makes RLHF training more stable and prevents the model from overfitting to the reward or drifting away from safe behavior. The paper gives a clear, gradient-based reason to choose the right KL form, which helps:
- Build more reliable training pipelines.
- Avoid subtle bugs that cause noisy or unstable learning.
- Decide between common methods like PPO and GRPO with a solid theory, not just “this estimator looks good.”
Implications and impact
- If you’re doing RLHF: prefer “k1 in reward” or “k2 as loss” for the KL penalty. They’re equivalent (on-policy), principled, and stable.
- Be cautious with “k3 as loss” (GRPO-style). It’s a shortcut that can be useful near the reference but can misbehave when far from it.
- If training off-policy: apply importance sampling and PPO clipping to the KL term, not just the reward part.
- For extra stability under big updates, consider bounded alternatives that keep the gradient within safe limits.
Overall, this paper helps the community stop thinking about KL regularization as “just estimating a number” and start thinking about “getting the right push.” That change leads to better, more robust RLHF systems.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a focused list of what remains missing, uncertain, or unexplored, distilled to guide future research.
- Off-policy correctness and practice: The paper identifies missing importance sampling (IS) and PPO-style clipping for “k_n as loss” in off-policy updates but provides neither full derivations nor experimental validation. What is the exact, implementable IS/clipping form for k2-as-loss, and how does it affect stability, sample efficiency, and bias in multi-epoch PPO-style training?
- Token-level vs sequence-level analysis: The theory collapses the sequence to a single action (bandit view). Do the on-policy gradient equivalence claims (k1-in-reward ≡ k2-as-loss) still hold with per-token score functions, truncated BPTT, length-normalization, baselines, and per-token clipping used in real RLHF?
- Stale policy and multi-epoch updates: The equivalence assumes on-policy sampling with a snapshot equal to the trainable policy at gradient time. How does equivalence degrade with multiple optimization epochs per rollout, stale ratios, and trust-region constraints?
- Quantifying the proposed off-policy correction: The paper proposes “a principled correction” for as-loss KL but does not empirically test it. What are the measured impacts on variance, convergence, and final performance across tasks, models, and β settings?
- Sensitivity to β and scheduling: Only a single β is used (0.5). How do the different KL forms behave across β schedules (warm-up, cosine, adaptive per-batch), and can adaptive β controllers reduce instability and reward hacking without degrading performance?
- Broader task and scale generalization: Experiments are on a small math subset with rule-based rewards and a 1.5B model. Do conclusions transfer to:
- larger models and longer contexts,
- code, dialogue, safety alignment, and multimodal tasks,
- human preference-trained reward models rather than rule-based signals?
- Interaction with entropy regularization: The experiments disable entropy loss. How do entropy bonuses interact with RKL under k1-in-reward vs k2-as-loss (complementarity, redundancy, or interference), and what are best practices for joint tuning?
- Advantage shaping and baselines: The analysis largely omits the effects of advantage normalization, baselines, and group/relative advantages (as in GRPO) on the KL gradient signal. Do these operations alter the effective equivalence or bias of different KL forms?
- Rigorous variance characterization: The paper argues k3-as-loss inherits chi-square-divergence variance but does not quantify gradient variance or sample efficiency empirically. How do gradient noise properties compare (k1-in-reward, k2-as-loss, k3-as-loss) across training phases?
- Regimes where k3 is acceptable: The paper frames k3-as-loss as a first-order surrogate but does not delineate safe usage regions. Can we specify quantitative conditions (e.g., bounds on χ²(πref||πθ), support overlap, or max KL) under which k3 behaves comparably to k2?
- Better-than-first-order surrogates: Is there a practically stable second-order or curvature-aware surrogate that more closely matches −log δ than k3-as-loss while retaining robustness in tails?
- Bounded-gradient alternatives: The MiniMax-01 MSE-style penalty is mentioned but not evaluated. Do bounded-coefficient penalties improve stability under large updates, and what trade-offs arise in constraint tightness and reward maximization?
- Dynamic or hybrid KL strategies: The paper notes k3-as-loss may be “milder” late-stage but provides no switching or mixing strategy. Can a principled curriculum/hybrid (e.g., k3 early, k2 late, or state-dependent mixing) yield better stability-performance trade-offs?
- Moving reference models: Results assume a fixed reference policy. How do conclusions change when the reference is periodically reset or updated online (e.g., Prorl-style), and what is the correct KL/IS handling in that setting?
- Forward KL and general f-divergences: The framework focuses on reverse KL. Can the gradient-centric unification extend to forward KL, JS, χ², α-divergences, and other f-divergences, and what are their principled “in-reward” vs “as-loss” implementations?
- Relationship to DPO and related “RL-free” methods: The paper cites DPO but does not analyze connections. Can the gradient-centric view explain when DPO-style objectives approximate RKL gradients, and how to combine or transition between DPO and RLHF with principled KL?
- Sampling and support issues: Real decoding often uses top-k/top-p sampling. How do truncation and support mismatch affect the stability and bias of k2-as-loss and k3-as-loss, especially under off-policy reuse?
- Numerical and implementation stability: The analysis highlights tail pathologies for k3 but does not provide guardrails. What are robust numerical practices (log-prob floor, gradient clipping of KL coefficients, calibration of logits) that preserve the intended gradient?
- Convergence guarantees: There is no formal convergence/regret analysis for the recommended KL implementations in policy-gradient RLHF. Under what conditions (step sizes, β schedules, clipping) can we guarantee stability or bounded regret?
- Human preference noise and misspecification: The paper motivates KL as a defense against reward misspecification but does not quantify it. How do different KL forms mitigate reward model bias/noise, and can we calibrate β based on uncertainty estimates?
- Multi-objective RLHF: Practical alignment often uses multiple reward components (helpfulness, harmlessness, calibration). How should KL regularization be integrated and balanced across multi-objective settings without destabilizing training?
- Comprehensive benchmarks and significance: Reported results emphasize training dynamics; downstream benchmarks and large-scale results are deferred to the appendix. Rigorous, cross-domain benchmarks with statistical significance are needed to validate generality.
- Reproducibility details: The exact “principled correction” implementation, token-level objective forms, and PPO/clip integration for as-loss KL are not fully specified in the main text. Public, minimal reference implementations would reduce ambiguity.
- Safety outcomes: The claim that stronger RKL helps prevent over-optimization is plausible but untested on safety metrics. Does k2-as-loss reduce harmful content or mode collapse relative to k3-as-loss and no-KL baselines in safety-alignment scenarios?
Practical Applications
Practical Applications of “Rethinking KL Regularization in RLHF: From Value Estimation to Gradient Optimization”
The paper offers a gradient-centric framework and concrete implementation guidance for KL regularization in RLHF, resolving common pitfalls and proposing principled alternatives. Below are actionable applications categorized by deployment horizon, linked to sectors and workflows, with noted assumptions and dependencies.
Immediate Applications
These can be deployed with current tools and practices.
- RLHF training pipelines: replace biased or vacuous KL losses
- Sectors: software (LLM platforms), education tech, healthcare, finance, robotics (task-oriented LLMs)
- Application: update RLHF implementations to use either “k1 in reward” (log-prob ratio as a detached coefficient inside policy gradient) or “k2 as loss” (squared log-prob ratio with backprop), instead of “k3 as loss.”
- Tools/workflows:
- In PPO-style training: combine reward and KL into a single policy gradient coefficient: r − β·(log πθ − log πref).
- In GRPO-style training: switch to k2 as loss (0.5·(log(π/πref))2) and ensure on-policy evaluation or apply off-policy corrections (see below).
- Assumptions/dependencies:
- On-policy gradient equivalence holds when samples are drawn from a detached snapshot equal to the trainable policy at gradient time.
- Reverse KL (RKL) setup; token-level implementations should preserve the detached-coefficient logic.
- Off-policy correctness for “as loss” KL terms in PPO-like updates
- Sectors: software (RLHF libraries: OpenRLHF, TRL, Verl, ROLL), enterprise AI training services
- Application: apply importance sampling (IS) and PPO clipping to the KL loss when using “k_n as loss” off-policy to remove bias.
- Tools/workflows:
- Weight KL loss terms with the IS ratio r = πθ(y|x)/πold(y|x) and apply PPO clipping to the ratio inside the KL term’s contribution.
- Alternatively, migrate to “k1 in reward” combined with PPO to inherit IS/clipping automatically.
- Assumptions/dependencies:
- Access to behavior policy probabilities for IS.
- Correct handling of detached vs. differentiable terms in code.
- Gradient-based diagnostics and safety monitors for KL regularization
- Sectors: software, platform reliability, model governance
- Application: add real-time monitors for KL gradient coefficients and variance to detect instability and bias.
- Tools/workflows:
- Track c(y|x) = log(πθ/πref) vs. c(y|x) = 1 − πref/πθ; flag tail behavior (πθ ≪ πref or πθ ≫ πref) and high chi-square divergence regions.
- Log distributions of KL coefficients and alert when coefficients saturate (k3) or explode.
- Assumptions/dependencies:
- Reliable access to πθ and πref token-level probabilities.
- Logging/telemetry integrated into training loops.
- Stability-first KL alternatives for large updates
- Sectors: high-stakes deployments (healthcare, finance), safety-focused labs
- Application: use bounded-gradient penalties (e.g., MiniMax-01/MSE-style penalties) when aggressive updates cause instability.
- Tools/workflows:
- Swap KL loss to a bounded gradient alternative during phases of large policy shifts; use dynamic scheduling to revert to principled KL later.
- Assumptions/dependencies:
- Acceptance of potential deviation from exact RKL; empirical validation on target tasks.
- Reference-model management to prevent drift and reward hacking
- Sectors: industry RLHF teams, applied research
- Application: pair principled KL with periodic reference resets (as observed in related work) to retain alignment and avoid overfitting.
- Tools/workflows:
- Maintain snapshots of the actor as refreshed references at scheduled intervals; adjust β accordingly.
- Assumptions/dependencies:
- Operational processes for snapshotting and evaluation; careful β scheduling.
- Developer-facing upgrades in open-source RLHF frameworks
- Sectors: software ecosystems (OpenRLHF, TRL, Verl, ROLL)
- Application: submit PRs or adopt forks that:
- Add “k2 as loss” with correct on-policy sampling,
- Fix off-policy bias for “as loss” KL by applying IS and PPO clipping,
- Provide configuration flags to select k1-in-reward/k2-as-loss, with defaults set to principled implementations.
- Tools/workflows:
- Training templates and scripts demonstrating correct KL usage across tasks (math/code/chat).
- Governance and compliance artifacts for RLHF processes
- Sectors: policy, enterprise risk/compliance
- Application: produce audit trails demonstrating use of principled KL (RKL) and bias corrections.
- Tools/workflows:
- Compliance dashboards: show distributions of KL coefficients, IS ratios, PPO clips applied, and evidence of on-policy equivalence when applicable.
- Assumptions/dependencies:
- Organizational buy-in; minimal overhead to log and report.
- Educator and practitioner training materials
- Sectors: academia, professional training, MOOCs
- Application: update curricula to emphasize gradient-centric KL, counterexamples (k1-as-loss), and on-/off-policy nuances.
- Tools/workflows:
- Interactive visualizations of coefficient curves and variance behavior; lab assignments using small LLMs to reproduce the paper’s findings.
- Assumptions/dependencies:
- Access to modest compute and open-source models.
Long-Term Applications
These require further research, scaling, or development effort.
- Adaptive KL schedulers and automated optimizer selection
- Sectors: AI platforms, enterprise ML Ops
- Application: auto-select KL formulation and dynamically schedule β based on real-time gradient statistics, tail behavior, and variance.
- Tools/products/workflows:
- “KL Controller” service that monitors c(y|x), variance, and divergence metrics, switching between k1-in-reward, k2-as-loss, or bounded alternatives, and adjusting β adaptively.
- Assumptions/dependencies:
- Robust online diagnostics; safe switching policies; extensive validation.
- Standardized RLHF governance metrics and benchmarks centered on gradient properties
- Sectors: policy, industry consortia, standards bodies
- Application: define and adopt gradient-based stability and bias metrics (e.g., coefficient distributions, chi-square divergence exposure) as part of alignment benchmarks and governance audits.
- Tools/products/workflows:
- Public benchmark suites and reporting templates; third-party auditing services (“KL Auditor”).
- Assumptions/dependencies:
- Community consensus on metrics; shared datasets and protocols.
- Token-level theory and generalized proofs under realistic training regimes
- Sectors: academia, research labs
- Application: extend the on-policy gradient-equivalence proof from the bandit (sequence-as-single-action) setting to full token-level, multi-step PPO with diverse reward shaping.
- Tools/products/workflows:
- Formal analysis and reference implementations; unit tests demonstrating equivalence across tokenization schemes and batching strategies.
- Assumptions/dependencies:
- Mathematical and empirical rigor; broad model/task coverage.
- Robust off-policy RLHF algorithms with principled KL in large-scale production
- Sectors: cloud AI services, large model training (vLLM rollouts)
- Application: design scalable off-policy RLHF that correctly integrates KL “as loss” with IS/clipping across distributed sampling, with guarantees on bias and variance.
- Tools/products/workflows:
- “IS-corrected GRPO” variants; distributed training libraries with native support for KL diagnostics and corrections.
- Assumptions/dependencies:
- Efficient probability logging at scale; reproducible distributed training semantics.
- Cross-modal alignment adopting gradient-correct KL regularization
- Sectors: vision, audio, diffusion models, 3D generation
- Application: apply the gradient-centric KL framework to preference-aligned diffusion and multimodal generative models, replacing heuristic KL surrogates with principled RKL implementations.
- Tools/products/workflows:
- Extensions in Diffusers and multimodal RLHF libraries; case studies in alignment of text-to-image/video/3D with human feedback.
- Assumptions/dependencies:
- Adaptation of KL terms to continuous-time likelihoods; modality-specific evaluation.
- Safety-first pipelines in regulated domains
- Sectors: healthcare, finance, legal
- Application: build “safe fine-tuning” processes that mandate principled KL and stability monitors to control distribution drift and reward hacking risks in domain-specific LLMs.
- Tools/products/workflows:
- Compliance-grade RLHF toolkits with dashboards, alerts, and audit-ready logs; integration with model cards and risk registers.
- Assumptions/dependencies:
- Domain approval and regulatory integration; rigorous human preference/reward modeling.
- Educational platforms and visualization tools
- Sectors: academia, developer education
- Application: interactive platforms for learning gradient-based KL, showing how k1-in-reward/k2-as-loss match true RKL gradients and why k3-as-loss can destabilize.
- Tools/products/workflows:
- Web-based simulators, notebooks, and visual dashboards; standardized teaching modules.
- Assumptions/dependencies:
- Funding and community adoption; maintenance and updates.
Key Assumptions and Dependencies Across Applications
- On-policy equivalence requirement: the principled equivalence between “k1 in reward” and “k2 as loss” depends on sampling from a detached snapshot numerically equal to the trainable policy at gradient time.
- Reverse KL context: results target reverse KL (expectation under current policy), not forward KL.
- Off-policy corrections: importance sampling and PPO clipping must be applied to “as loss” KL terms to avoid bias.
- Distributional considerations: “k3 as loss” is tolerable only when πθ and πref are close; it is biased and can be unstable in tails or support mismatches.
- Token-level implementation details: while the paper analyzes sequence-level (bandit) probability, practitioners must preserve detached vs. differentiable paths in token-level PPO implementations.
- Reward model and data quality: benefits depend on reliable preference signals and clean rollout data; extreme reward shaping can interact with KL and must be validated.
Glossary
- Advantage signal: A shaped version of the reward used to reduce variance and improve learning in policy gradient methods. "Practical implementations replace the raw reward with a shaped advantage signal."
- Actor model: The trainable policy network in RLHF that generates responses and receives gradient updates. "RLHF regularizes the actor model to the reference model via the RKL:"
- Bandit setting: A simplified RL setting where each decision is treated as a single action with associated reward, without state transitions. "and follow the standard bandit setting."
- Baseline (policy gradients): A reference value subtracted from rewards to reduce variance in policy gradient estimates. "precisely the exact mechanism that underlies the subtraction of the baseline in policy gradients such as REINFORCE"
- Chi-square divergence: A statistical divergence measuring distribution mismatch, often high-variance and unstable compared to KL. "=\chi2(\pi_{\text{ref}\Vert\pi_{\theta}), the chi-square divergence, which is notoriously unstable."
- Clipped surrogate objective: PPO’s objective that clips the probability ratio to limit update magnitude and improve stability. "when combined with PPO, this correction is automatically inherited via the clipped surrogate objective $\pi_{red{\theta}/{\pi_{\theta_k}$."
- Combined form: Integrating reward and KL regularization into a single score-function term with a merged coefficient. "its coefficient can be merged into the reward coefficient to produce a Combined Form—hence the name `in reward':"
- Decoupled form: Separating the reward objective and KL loss into distinct terms, each optimized individually. "In contrast, ` as loss' necessitates a Decoupled form with a separate loss form:"
- Detached coefficient: A scalar weight multiplying the score function that does not carry gradients (i.e., is treated as constant during backprop). "Treats as a detached coefficient weight for the score function."
- Detached snapshot policy: A frozen copy of the current policy used for sampling, ensuring gradients flow only through the live policy. "Samples are drawn from a detached and numerically identical snapshot policy "
- Entropy loss: A regularizer that encourages exploration by increasing output distribution entropy. "We turn off the entropy loss (coefficient 0)"
- Forward KL: KL divergence measured as expectation under the reference distribution, typically harder to estimate on-policy in RLHF. "By contrast, Forward KL expectation is under $\pi_{\text{ref}(\cdot|x)$ and thus hard to be estimated from on-policy samples, making it rarely used in RLHF."
- Gradient-equivalent: Two losses are gradient-equivalent if they produce the same expected gradient under the same sampling conditions. "are principled, gradient-equivalent, and interchangeable implementations of RKL regularization under on-policy sampling."
- GRPO: An RLHF variant that uses a specific KL loss formulation (commonly k3) and often omits certain off-policy corrections. "More recently, the GRPO method \citep{shao2024deepseekmath}, utilized in influential models such as DeepSeek-R1 \citep{guo2025deepseek}, has gained prominence by adopting the term directly as a KL loss."
- Importance ratio: The ratio of reference to current probabilities used in estimators and importance sampling corrections. "Given the importance ratio , common estimators for the term within the expectation include:"
- Importance sampling: A technique to correct bias when optimizing with samples drawn from a distribution different from the one defining the objective. "biased due to neglected importance sampling, and we propose a principled correction."
- Kullback-Leibler (KL) divergence: A measure of how one probability distribution diverges from another, used to regularize policies. "The Kullback-Leibler (KL) divergence from a distribution to a reference is defined as:"
- Log-derivative trick: A technique to rewrite gradients of expectations so they can be estimated with the score function. "Applying the product rule and the log-derivative trick to RKL"
- MiniMax-01 loss: A bounded alternative penalty whose induced gradient coefficients lie within [-1, 1] to improve stability. "For example, the MSE-based penalty, like the MiniMax-01 loss, induces a coefficient bounded within ."
- Monte Carlo sampling: Estimating expectations by averaging over randomly sampled data points. "Since the expectation of the KL divergence is often intractable, it is typically estimated by Monte Carlo sampling."
- Off-policy: Using data sampled from a behavior policy different from the current trainable policy, which requires bias corrections. "For off-policy updates, explicit importance sampling and PPO clip are required, as discussed in~\Cref{sec:offpolicy}."
- On-policy: Using data sampled from the current policy being optimized, enabling unbiased gradient estimation. "Its expectation is taken under the current policy, making on-policy Monte Carlo estimation a natural choice."
- Policy gradient: A class of methods that directly optimize the parameters of a policy by following the gradient of expected reward. "the subtraction of the baseline in policy gradients such as REINFORCE"
- PPO: Proximal Policy Optimization, a stable policy-gradient algorithm that uses clipped objectives and often integrates KL as a reward coefficient. "PPO is a canonical example of using ` in reward' in a combined form."
- PPO clip: The clipping mechanism in PPO that bounds the probability ratio to prevent overly large policy updates. "For off-policy updates, explicit importance sampling and PPO clip are required, as discussed in~\Cref{sec:offpolicy}."
- Reference model: A fixed policy the current actor is regularized toward to prevent drift and overfitting. "RLHF regularizes the actor model to the reference model via the RKL:"
- Reinforcement Learning from Human Feedback (RLHF): A post-training method that uses human preference signals to fine-tune LLMs with reward and KL regularization. "Reinforcement Learning from Human Feedback (RLHF) leverages a Kullback-Leibler (KL) divergence loss to stabilize training and prevent overfitting."
- Reverse KL (RKL): KL divergence measured as expectation under the current policy, commonly used to regularize policies toward a reference. "RLHF regularizes the actor model to the reference model via the RKL:"
- Reward hacking: Exploitative behavior where a policy maximizes the learned reward in unintended ways, degrading alignment. "Pure reward maximization may cause reward hacking and distribution drift from a trusted SFT policy."
- Score function: The gradient of the log probability of the policy, used in policy gradient estimators. "the score function $\nabla_{red{\theta}\log\pi_{red{\theta}(y|x)$"
- Score function estimator: The REINFORCE-style estimator that uses the score function to estimate gradients of expected reward. "The gradient of this objective is typically estimated using the score function estimator \citep{williams1992simple}"
- Surrogate loss: An alternative objective designed to produce the same or similar gradient as a target objective. "The following theorem shows that two structurally different surrogate losses do so exactly."
- Taylor surrogate: A first-order approximation used to replace a principled coefficient or loss, trading accuracy for simplicity. "Thus, is only a first-order surrogate of the principal coefficient ."
- Zero-mean score identity: The property that the expected score function under its own distribution is zero, used to simplify gradient expressions. "By the zero-mean score identity in~\Cref{lem:zero-mean-score}, the term '+1' vanishes in expectation"
Collections
Sign up for free to add this paper to one or more collections.