Prompt Curriculum Learning for Efficient LLM Post-Training (2510.01135v1)

Abstract: We introduce Prompt Curriculum Learning (PCL), a lightweight reinforcement learning (RL) algorithm that selects intermediate-difficulty prompts using a learned value model to post-train LLMs. Since post-training LLMs via RL remains sensitive to batching and prompt selection strategies, we first conduct a series of systematic experiments where we (1) determine the optimal training batch size that balances generation efficiency and gradient quality and (2) establish the importance of focusing on prompts of intermediate difficulty for the policy. We build upon these results to design PCL, which identifies prompts of intermediate difficulty for the current policy in an on-policy manner by using a value model that is concurrently updated based on the current policy. By focusing on informative prompts that yield high effective ratios, PCL achieves either the highest performance or requires significantly less time to reach comparable performance to its counterparts. Compared to rollout-based filtering methods, PCL avoids costly rollouts and achieves $12.1\times$ and $16.9\times$ faster speed on identifying intermediate-difficulty prompts when training on MATH and DeepScaleR, respectively. We further demonstrate that our value model accurately predicts prompt difficulty and allows PCL to focus on progressively more challenging prompts during RL. Our results present a new methodology that delivers improved tradeoff between upper-bound performance and efficiency for reasoning-focused RL.

• The paper introduces a reinforcement learning approach called Prompt Curriculum Learning (PCL) that selects intermediate-difficulty prompts to boost LLM post-training efficiency.
• It empirically identifies optimal batch sizes and decomposition strategies, achieving 12.1×–16.9× faster prompt filtering compared to rollout methods.
• The method leverages a value model to dynamically match target difficulty, ensuring superior sample efficiency and faster convergence with minimal overhead.

Prompt Curriculum Learning for Efficient LLM Post-Training: A Technical Analysis

Introduction

This work introduces Prompt Curriculum Learning (PCL), a reinforcement learning (RL) algorithm for post-training LLMs that leverages a value model to select prompts of intermediate difficulty. The motivation is rooted in the observation that RL-based post-training of LLMs is highly sensitive to both batching strategies and prompt selection, with significant implications for convergence speed, sample efficiency, and computational cost. The authors conduct a comprehensive empirical paper to identify optimal batch configurations and prompt difficulty regimes, and subsequently design PCL to exploit these findings for efficient and effective LLM post-training.

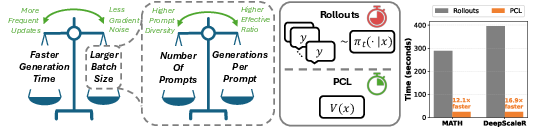
Figure 1: Systematic investigation of generation time vs. batch size and prompt difficulty, motivating PCL. PCL achieves 12.1× and 16.9× faster prompt filtering than rollout-based methods on MATH and DeepScaleR, respectively.

Empirical Analysis of Batch Size and Prompt Difficulty

Batch Size and Generation Efficiency

The paper systematically explores the trade-off between batch size, generation time, and gradient quality. Larger batch sizes reduce gradient noise and enable higher learning rates, but increase generation time, which can bottleneck update frequency. The authors identify a critical transition point: generation time initially grows sublinearly with batch size, then transitions to linear scaling as compute utilization saturates. The optimal batch size for convergence speed is found at this transition, typically around 8K prompt-response pairs for the tested configurations.

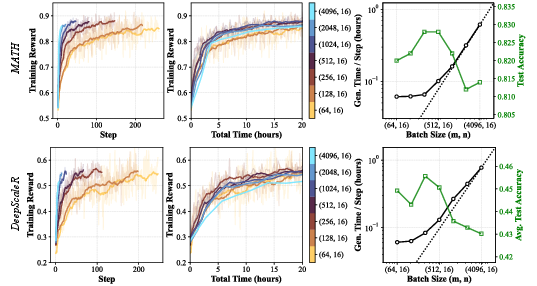
Figure 2: Training reward and wall-clock time for Qwen3-4B-Base on MATH and DeepScaleR, with generation time and test accuracy across batch sizes. The optimal batch size is at the sublinear-to-linear transition.

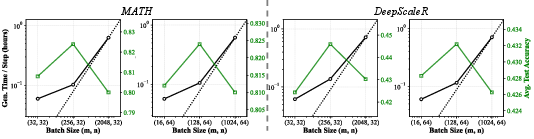
Figure 3: Generation time per step and test accuracy for various (number of prompts, generations per prompt) batch decompositions.

Decomposition: Number of Prompts vs. Generations per Prompt

The batch size can be decomposed into the number of unique prompts ($m$) and the number of generations per prompt ($n$). Increasing $m$ enhances prompt diversity, reducing gradient noise, while increasing $n$ improves the effective ratio—the proportion of samples with non-zero advantage, which is critical for stable learning. The analysis reveals that prompts of intermediate difficulty ($p(x) \approx 0.5$) maximize both the effective ratio and gradient norm, leading to superior sample efficiency and test accuracy.

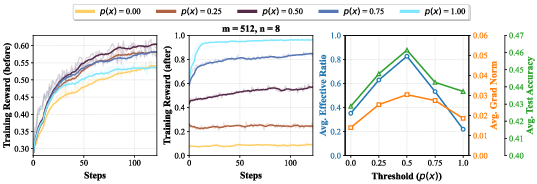
Figure 4: Training reward before and after downsampling, effective ratio, gradient norm, and test accuracy across prompt difficulty thresholds.

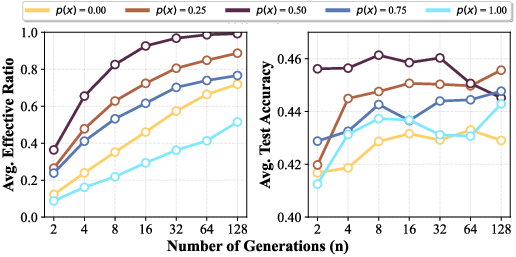
Figure 5: Effective ratio and test accuracy as a function of prompt difficulty threshold and generations per prompt.

Prompt Curriculum Learning (PCL): Algorithmic Design

PCL is designed to efficiently select prompts of intermediate difficulty using a value model $V(x)$, which predicts the expected reward for each prompt under the current policy. At each iteration, a large pool of candidate prompts is sampled, and $V(x)$ is used to select those closest to a target threshold (typically $\tau=0.5$). This approach avoids the computational overhead of rollout-based filtering and the off-policyness of dictionary-based methods.

The value model is trained online, minimizing the squared error between its prediction and the empirical average reward over $n$ generations for each selected prompt. The computational cost of training and inference for the value model is negligible compared to full rollouts.

PCL Algorithm (high-level):

1. Sample $km$ candidate prompts.
2. Use $V(x)$ to select $m$ prompts with $|V(x) - \tau|$ minimized.
3. For each selected prompt, generate $n$ responses with the current policy.
4. Update the policy using standard policy gradient.
5. Update $V(x)$ using the observed rewards.

Experimental Results

PCL is benchmarked against several baselines, including:

• GRPO: No prompt filtering, uniform sampling.
• Pre-filter: Filters prompts using a fixed reference policy.
• Dynamic Sampling (DS): Uses rollouts to estimate $p_\pi(x)$ for filtering.
• SPEED: Pre-generates rollouts for filtering, but introduces off-policyness.
• GRESO: Dictionary-based historical reward tracking.

PCL consistently achieves either the highest performance or requires significantly less training time to reach comparable performance across Qwen3-Base (1.7B, 4B, 8B) and Llama3.2-it (3B) on MATH, DeepScaleR, and other mathematical reasoning benchmarks.

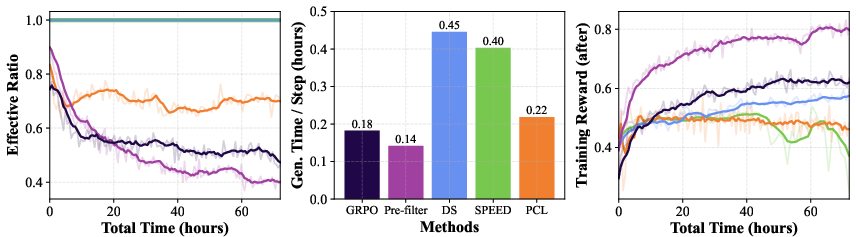
Figure 6: On DeepScaleR with Qwen3-8B-Base, PCL achieves higher effective ratio or lower generation time compared to baselines, and consistently focuses on $p(x)=0.5$ prompts.

PCL's value model achieves explained variance comparable to using three rollouts per prompt for difficulty estimation, but with a 12.1×–16.9× speedup in prompt filtering.

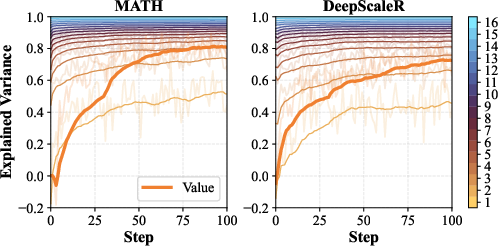
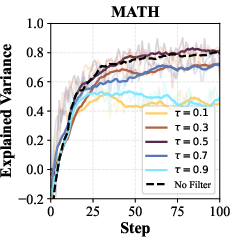
Figure 7: Explained variance of PCL's value model compared to using 1–16 rollouts for difficulty estimation.

Analysis and Ablations

• Effective Ratio and Generation Time: PCL maintains a high effective ratio with minimal generation overhead, unlike DS and SPEED, which incur substantial generation costs.
• Value Model Accuracy: The value model's accuracy is robust to filtering, with best performance at $\tau=0.5$.
• Curriculum Dynamics: As the policy improves, PCL naturally shifts focus to harder prompts, even with a fixed threshold, due to the evolving policy competence.

Theoretical Insights

The squared norm of the policy gradient is maximized for prompts with $p(x) = 0.5$, as shown by the variance of the advantage estimator:

$$\mathbb{E}_{y \sim \pi(\cdot|x)}[A(x, y)^2] = p_\pi(x)(1 - p_\pi(x))$$

This justifies the curriculum strategy of focusing on intermediate-difficulty prompts for maximal learning signal.

Implementation Considerations

• Batch Size Tuning: The optimal batch size is hardware- and context-length-dependent; practitioners should empirically identify the sublinear-to-linear transition point for their setup.
• Value Model Architecture: Using a value model of similar size to the policy yields faster convergence, especially on large datasets.
• Scalability: PCL is compatible with both synchronous and asynchronous RL pipelines, though the current paper focuses on synchronous settings.
• Reward Generality: While the paper uses binary rewards, PCL extends naturally to scalar rewards by adjusting the target threshold.

Limitations and Future Directions

• On-Policy Restriction: The analysis and experiments are limited to purely on-policy RL; extension to off-policy or replay-buffer-based pipelines may require further adaptation.
• Synchronous Training: Asynchronous RL settings, common in large-scale deployments, may necessitate more sophisticated value model synchronization.
• Context Length: Experiments are limited to 4K tokens; longer contexts may shift the optimal batch size and prompt selection dynamics.
• Generalization: The assumption that training on intermediate prompts generalizes to easier and harder prompts may not hold in all domains.

Conclusion

Prompt Curriculum Learning (PCL) provides an efficient and principled approach to LLM post-training by leveraging a value model for online prompt selection. By focusing on intermediate-difficulty prompts and optimizing batch configuration, PCL achieves superior sample efficiency and convergence speed compared to existing methods, with substantial reductions in computational overhead. The methodology is theoretically grounded and empirically validated across multiple models and datasets. Future work should explore extensions to asynchronous and off-policy RL, as well as applications beyond mathematical reasoning.