Lectures on Open Effective Field Theories (2510.00140v1)

Abstract: Effective field theories offer a powerful method to unify diverse models under a small set of control parameters, allowing systematic expansions around well-established theories. These techniques, developed in particle physics, were designed for experiments where the initial state - the vacuum before a scattering event - is as clean and isolated as possible. Besides colliders, realistic environments are often noisy and dissipative. The recognition of the limitations of traditional EFT techniques has, over the past decade, sparked intense progress at the interface of high-energy physics and condensed matter. These considerations motivate a new approach to gravitation and cosmology, one that models the gravitational sector as evolving in the presence of an unobservable medium. Open Effective Field Theories provide a systematic and controllable field-theoretic framework for modeling dissipation and noise in gravitation and cosmology. These notes aim to introduce this versatile toolkit, enabling model-agnostic assessments of how unknown environments shape our observational probes.

• The paper develops a systematic framework for open effective field theories that incorporates dissipation and noise beyond traditional unitary models.
• It employs the Schwinger-Keldysh formalism to derive non-unitary operators, capturing stochastic dynamics emerging from integrating out heavy fields.
• Applications to cosmology, gauge theories, and gravity demonstrate practical methods for modeling open systems through effective actions.

Open Effective Field Theories: A Systematic Framework for Dissipation and Noise in Quantum Field Theory and Cosmology

Introduction and Motivation

The lecture notes "Lectures on Open Effective Field Theories" (2510.00140) provide a comprehensive and systematic treatment of open effective field theories (Open @@@@2@@@@), with a focus on their application to cosmology, gravitation, and gauge theories. The central motivation is to extend the traditional EFT paradigm—originally developed for isolated, unitary systems—to settings where the system of interest interacts with an unobservable environment, leading to dissipation, noise, and non-equilibrium dynamics. This is particularly relevant in cosmology, where direct experimental access to many degrees of freedom is impossible, and the observable sector is effectively "open" due to its coupling to unknown or inaccessible sectors.

The notes are structured as a sequence of lectures, each building up the formalism and its applications:

1. Schwinger-Keldysh Formalism: Introduction to the in-in (Schwinger-Keldysh) path integral, which is essential for computing real-time correlation functions in open and non-equilibrium systems.
2. Open Scalar Theories: Construction of open EFTs for scalar fields, including the classification of dissipative and stochastic operators.
3. Open Inflation: Application of the open EFT framework to inflationary cosmology, generalizing the EFT of Inflation to include dissipation and noise.
4. Open Electromagnetism: Extension to Abelian gauge theories, with a detailed analysis of gauge invariance in the Schwinger-Keldysh contour.
5. Open Gravity: Formulation of open EFTs for gravity, including the interplay between diffeomorphism invariance and openness.

Schwinger-Keldysh Formalism and Path Integral Structure

The Schwinger-Keldysh (SK) or in-in formalism is the backbone of the open EFT approach. Unlike the in-out formalism used for S-matrix elements, the SK contour doubles the degrees of freedom, introducing "forward" ($+$) and "backward" ($-$) branches. This allows for the computation of expectation values and correlation functions in mixed states, accommodating the loss of information to an environment.

The path integral for the reduced density matrix $\rho_{\phi\phi'}(t)$ is given by

$$\rho_{\phi\phi'}(t) = \int^{\phi} \mathcal{D}\varphi_{+} \int^{\phi'} \mathcal{D} \varphi_{-} \, e^{iS_{\mathrm{eff}}[\varphi_{+},\varphi_{-}]}$$

where $S_{\mathrm{eff}}$ is the open effective action, which can be decomposed as

$$S_{\mathrm{eff}}[\varphi_+, \varphi_-] = S_{\mathrm{unit}}[\varphi_+] - S_{\mathrm{unit}}[\varphi_-] + F[\varphi_+, \varphi_-]$$

with $F$ the Feynman-Vernon influence functional encoding non-unitary effects (dissipation, noise).

The Keldysh basis, defined by $\varphi_r = (\varphi_+ + \varphi_-)/2$ and $\varphi_a = \varphi_+ - \varphi_-$, is particularly convenient for organizing the expansion and identifying the physical content of various terms.

Figure 1: Comparison between the single-branch (wavefunction) and double-branch (density matrix) path integral contours. The double-branch contour is essential for describing mixed states and open system dynamics.

Integrating Out Heavy Fields: Emergence of Dissipation and Noise

A key technical result is the explicit demonstration that integrating out heavy fields in the SK formalism generates not only the expected local (unitary) EFT operators, but also non-unitary terms corresponding to dissipation and noise. This is made manifest in the Keldysh basis, where the effective action contains both odd and even powers of $\varphi_a$:

• Odd powers (e.g., $\varphi_a$) correspond to dissipative terms.
• Even powers (e.g., $\varphi_a^2$) correspond to stochastic (noise) terms.

The expansion of correlation functions in the heavy mass limit reveals the appearance of odd powers of $1/M$ (where $M$ is the heavy mass), which cannot be captured by the standard $\Box/M^2$ expansion of the in-out formalism. These terms are directly associated with non-unitary effects and are absent in the S-matrix approach.

Figure 2: Illustration of the difference between amplitudes (in-out) and correlators (in-in). Integrating out heavy fields in the in-in framework generates dissipative and stochastic operators, leading to odd powers of $1/M$.

Open Scalar Theories: Operator Classification and Stochastic Dynamics

The open EFT for a scalar field is constructed by writing the most general local action consistent with the symmetries and the non-equilibrium constraints (normalization, Hermiticity, positivity). The action is organized as an expansion in powers of the advanced field $\varphi_a$:

$S_{\mathrm{eff}} = S_1 + S_2 + S_3 + \cdots$

where $S_n = \mathcal{O}(\varphi_a^n)$. The leading terms are:

• $S_1$: Dissipative (linear in $\varphi_a$), e.g., $\gamma \dot{\varphi}_r \varphi_a$.
• $S_2$: Noise (quadratic in $\varphi_a$), e.g., $i\beta \varphi_a^2$.
• $S_3$: Non-Gaussian noise (cubic in $\varphi_a$).

The stochastic dynamics is made explicit via the Hubbard-Stratonovich transformation, which introduces auxiliary noise fields and leads to Langevin-type equations for the system.

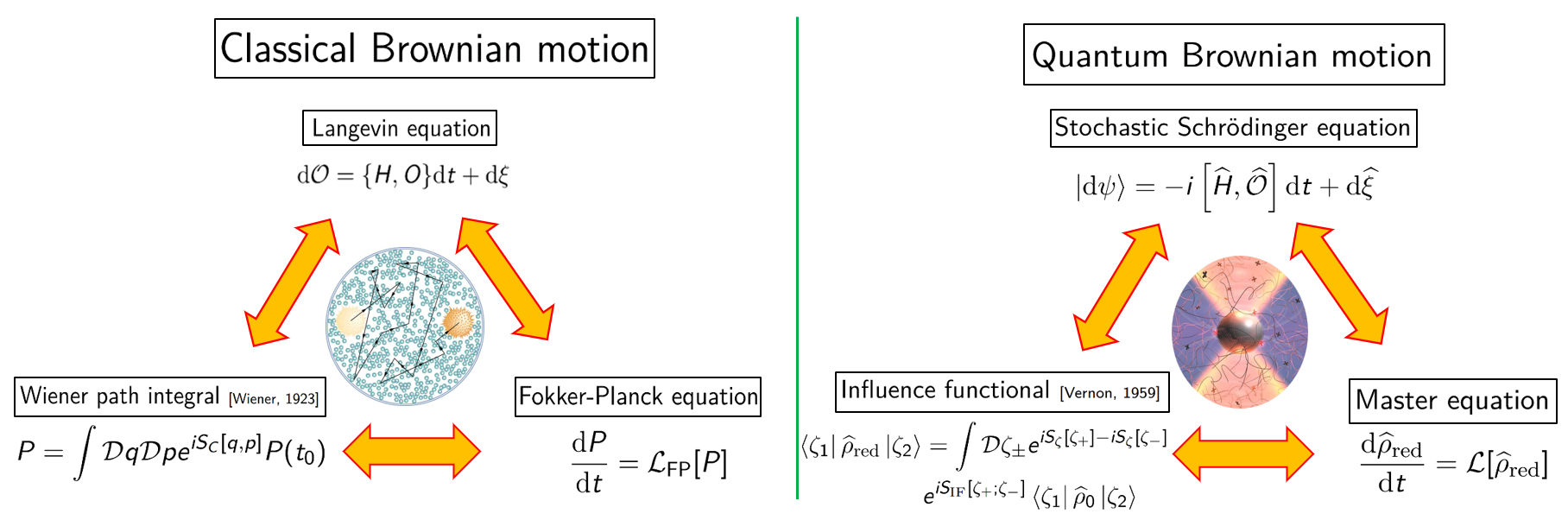
Figure 3: Open classical and quantum systems. The environment induces renormalization, dissipation, and noise, captured by the Langevin equation and its quantum analogs.

Open Inflation: Dissipation and Noise in the EFT of Inflation

The open EFT framework is applied to single-clock inflation, generalizing the EFT of Inflation (EFToI) to include dissipative and stochastic effects. The effective action for the Goldstone mode $\pi$ (arising from broken time translations) is constructed to be invariant under the residual symmetries (spatial diffs, non-linearly realized time diffs).

The quadratic action includes both unitary and non-unitary terms:

$$S^{(2)}_{\mathrm{eff}} = \int d^4x \left[ a^2 \pi'_r \pi'_a - c_s^2 a^2 \partial_i \pi_r \partial^i \pi_a - 2 a^3 \gamma_1 \pi'_r \pi_a + i\beta_1 a^4 \pi_a^2 + \cdots \right]$$

The resulting power spectrum and bispectrum exhibit distinctive features:

• Power spectrum: Enhanced or suppressed depending on the dissipation parameter $\gamma/H$ and the noise amplitude $\beta_1$.
• Bispectrum: New shapes and scaling behaviors, including regularized folded singularities and non-Gaussian noise contributions.

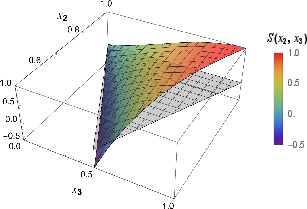
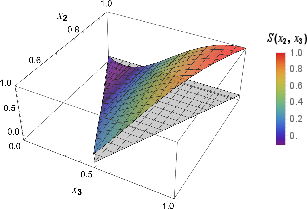
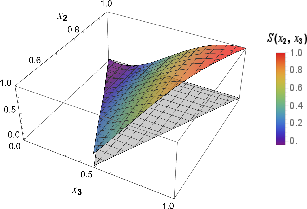
Figure 4: Shapes of the bispectrum at large dissipation ($\gamma = 5H$). The signal peaks in the equilateral configuration, and consistency relations hold in the squeezed limit.

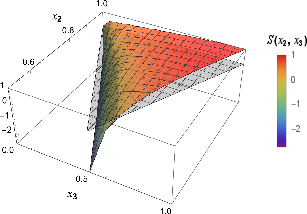
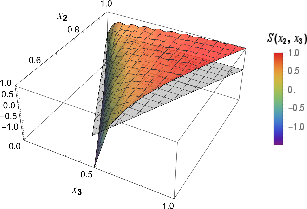
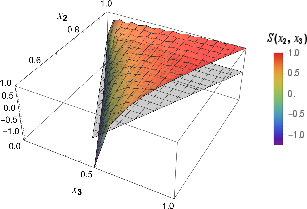
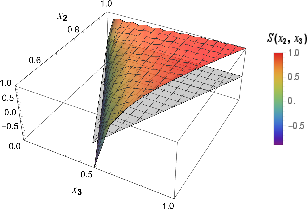
Figure 5: Shapes of the bispectrum at low dissipation ($\gamma = 0.001H$). The signal peaks near folded configurations, with regularized singularities due to dissipation.

Open Electromagnetism: Gauge Invariance and Dissipative Media

The extension to Abelian gauge theories is nontrivial due to the interplay between gauge invariance and openness. The effective action is constructed to be invariant under retarded gauge transformations, while advanced gauge invariance is generally broken by dissipative terms. The lack of advanced gauge invariance is directly related to the non-conservation of the system's current, reflecting the exchange of charge with the environment.

The most general quadratic action in Fourier space is

$$S_1 = \int_{\omega, k} \left[ a^0 (i k_i F^{0i} + j_0) + a_i (\gamma_2 F^{0i} + \gamma_3 i k_j F^{ij} + \cdots + j_i) \right]$$

The resulting equations of motion generalize Maxwell's equations to include dissipation and noise, and the formalism naturally recovers the standard theory of electromagnetism in a medium (with complex permittivity and permeability).

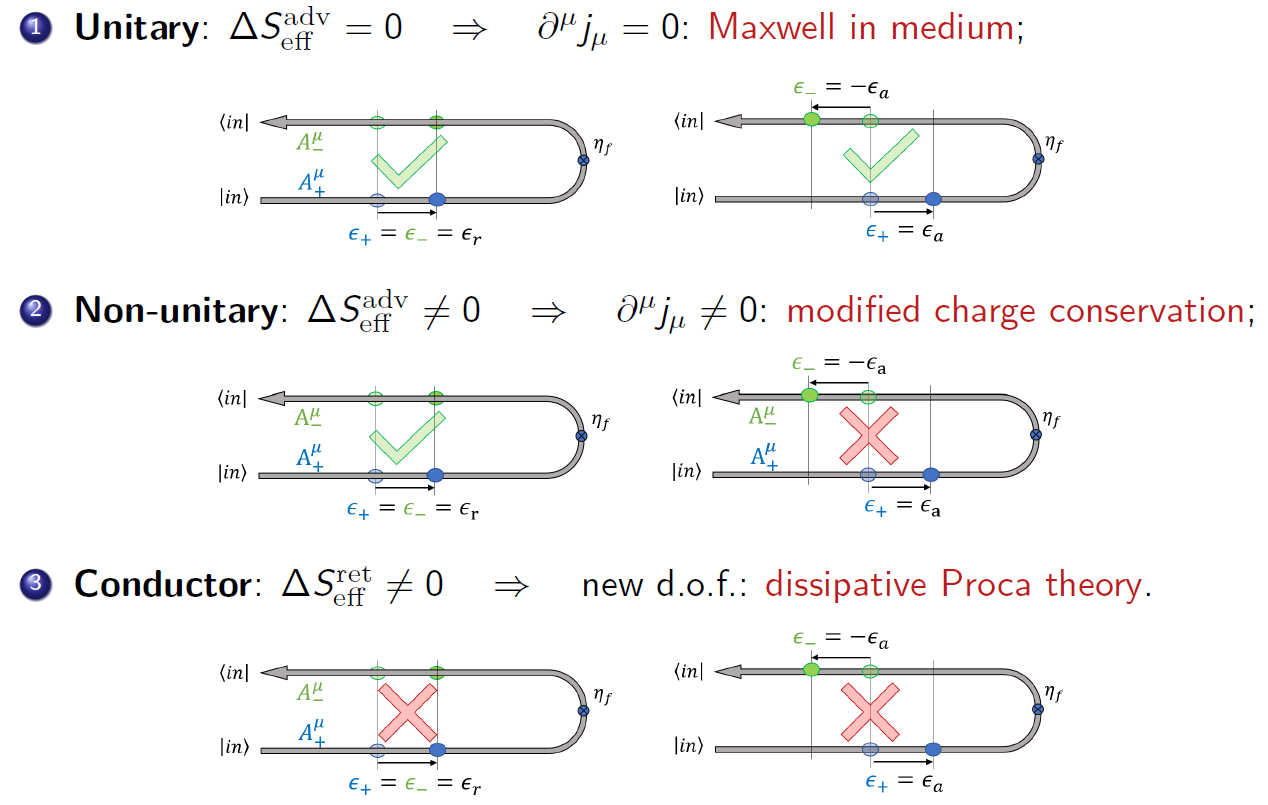
Figure 6: Consequences of influence functional invariance under retarded and advanced transformations. Only retarded gauge invariance is preserved in open systems, leading to non-standard current conservation.

Open Gravity: Diffeomorphism Invariance and Energy Exchange

The final lecture develops the open EFT for gravity, focusing on the interplay between diffeomorphism invariance and openness. The metric is doubled, and the effective action is constructed to be invariant under retarded diffeomorphisms (with advanced diffs broken by dissipative effects). The resulting modified Einstein equations take the form

$$G_{\mu\nu} + \text{modifications} = T^{(\text{sys})}_{\mu\nu}$$

where the modifications encode the influence of the environment. The non-conservation of the system's stress-energy tensor is a direct consequence of energy-momentum exchange with the environment:

$$\nabla^\mu T^{(\text{sys})}_{\mu\nu} = -\nabla^\mu T^{(\text{env})}_{\mu\nu}$$

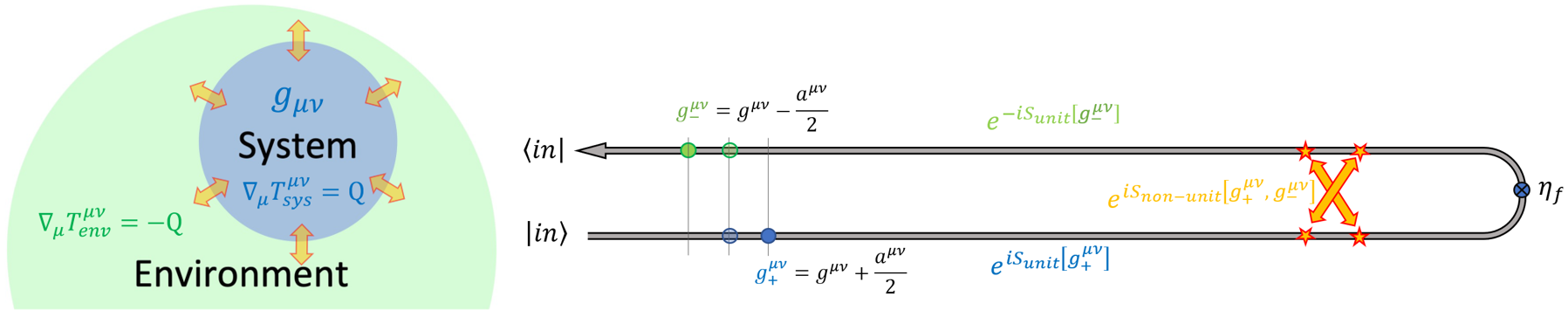
Figure 7: Illustration of the lack of conservation of the system's stress-energy tensor. Energy and momentum are exchanged between system and environment, consistent with total conservation.

Implementation and Practical Considerations

Operator Construction and Power Counting

• Symmetry constraints: All operators must respect the residual symmetries (e.g., spatial diffs, non-linearly realized time diffs).
• Non-equilibrium constraints: The effective action must satisfy normalization, Hermiticity, and positivity, leading to specific constraints on the allowed operators and their coefficients.
• Power counting: The expansion in $\varphi_a$ (or $a^\mu$ for gauge fields) provides a systematic way to organize the EFT, with higher powers corresponding to higher-order noise and non-Gaussian effects.

Computational Aspects

• Diagrammatics: Feynman rules in the Keldysh basis are provided, with explicit propagators for retarded, advanced, and Keldysh components.
• Numerical evaluation: Many observables (e.g., bispectra) require numerical integration due to the complexity of the time-dependent propagators and non-local kernels.
• Matching to UV models: The formalism allows for systematic matching to explicit microscopic models (e.g., gauge-inflation scenarios), with clear prescriptions for extracting the EFT coefficients.

Resource Requirements and Scaling

• Computational cost: The evaluation of multi-point functions in the SK formalism is more demanding than in the in-out formalism, due to the doubling of fields and the need to track all branch indices.
• Memory and storage: For large-scale cosmological applications (e.g., bispectrum estimation), efficient storage and manipulation of Keldysh propagators and kernels is essential.
• Parallelization: Many of the required integrals (e.g., for the bispectrum) are amenable to parallel computation.

Limitations and Extensions

• Separation of scales: The locality of the open EFT relies on a clear hierarchy between system and environment scales. Non-local effects (e.g., from light or resonant environments) require a more general treatment.
• Backreaction: The formalism typically neglects the backreaction of the system on the environment; including this requires a more elaborate treatment.
• Beyond leading order: Systematic inclusion of higher-order (non-Gaussian) noise and non-Markovian effects is possible but computationally intensive.

Implications and Future Directions

The open EFT framework provides a powerful and flexible toolkit for modeling dissipation, noise, and non-equilibrium effects in quantum field theory, cosmology, and gravitation. Its systematic operator classification, rooted in symmetry and non-equilibrium constraints, enables model-agnostic phenomenological studies and facilitates matching to explicit UV completions.

Potential future developments include:

• Bootstrap approaches: The analytic structure of dissipative correlators suggests the possibility of bootstrap techniques for open systems.
• Quantum information applications: The formalism is well-suited for studying decoherence, entanglement, and quantum-to-classical transitions in cosmological and gravitational settings.
• Extensions to non-Abelian gauge theories and higher-spin fields: The generalization of the open EFT approach to more complex field content is a promising direction.
• Numerical implementations for large-scale structure and CMB analyses: The framework can be integrated into pipelines for analyzing cosmological data, enabling robust constraints on dissipative and stochastic new physics.

Conclusion

"Lectures on Open Effective Field Theories" provide a rigorous and detailed foundation for the construction and application of open EFTs in a wide range of physical contexts. By systematically incorporating dissipation, noise, and non-equilibrium effects within a symmetry-based operator expansion, the framework enables both bottom-up phenomenology and top-down matching to UV models. The formalism is essential for the analysis of realistic, open quantum systems in cosmology and beyond, and sets the stage for future advances in both theoretical and observational directions.