Data-driven transient growth analysis (2509.18974v1)

Abstract: Transient growth analysis has been extensively studied in asymptotically stable flows to identify their short-term amplification of perturbations. Generally, in global transient growth analyses, matrix-free methods are adopted, requiring the construction of adjoint equations, either in the discrete or continuous form. This paper introduces a data-driven algorithm that circumvents the adjoint equations by extracting the optimal initial perturbation and its energy growth over a specified time horizon from transient snapshots of perturbations. This method is validated using data from the linearised complex Ginzburg-Landau equation, backward-facing step flow, and the Batchelor vortex. Unlike model-based methods, which require $S$ sets of integrations of the linearised governing equation and its adjoint for $S$ time horizons, the proposed approach collects the snapshots of $S$ time horizons in one integration of the linearised equation. Furthermore, this study provides a robust framework for utilising proper orthogonal decomposition (POD) modes to synthesise optimal modes. The developed capacity to conduct transient growth analyses without solving the adjoint equations is expected to significantly reduce the barriers to transient dynamics research.

• The paper introduces a data-driven method that avoids adjoint equations, significantly cutting computational complexity in transient growth analysis.
• It employs Proper Orthogonal Decomposition and Singular Value Decomposition to extract optimal modes from fluid dynamics data, validated through complex scenarios including the CGL equation and backward-facing step flow.
• The method demonstrates robust performance in both 2D and 3D flows, offering efficient predictions and paving the way for future applications in nonlinear and compressible flow regimes.

Data-Driven Transient Growth Analysis

Transient growth analysis plays a pivotal role in understanding the short-term amplification of perturbations in fluid dynamics, particularly in asymptotically stable flows. The paper "Data-driven transient growth analysis" introduces a novel approach to performing these analyses without the traditional reliance on adjoint equations. This method promises to simplify computational procedures significantly while maintaining accuracy, as demonstrated through several case studies involving the complex Ginzburg-Landau (CGL) equation, backward-facing step flow, and Batchelor vortex.

Methodology

Introduction to Data-Driven Approach

The conventional approach to transient growth analysis involves integrating both the forward and adjoint equations of the linearized Navier-Stokes equations, which is computationally intensive. The paper proposes a data-driven technique that relies solely on the forward operator, thereby circumventing the adjoint equations. This is achieved by collecting transient snapshots of perturbations and using Proper Orthogonal Decomposition (POD) to synthesize optimal modes.

Implementation Strategy

The method involves constructing a matrix of initial conditions using snapshots from trajectories initialized by Hermite polynomials, which are known for their orthogonal properties. These are projected onto a reduced-dimensional space through POD, forming the basis for further analysis. Subsequently, Singular Value Decomposition (SVD) is performed on the extracted modes to approximate the evolution operator without explicitly constructing it.

Validation and Case Studies

The proposed methodology was validated through three significant fluid dynamics problems:

1. Complex Ginzburg-Landau Equation: The analysis showed close agreement with model-based methods even with a smaller dataset of initial conditions. The method efficiently captured the short-term dynamics, demonstrating its potential for applications requiring rapid assessments.

   Figure 1: Data-driven transient growth analysis of the linearised complex Ginzburg-Landau equation showing the relative error between model-based and data-driven optimal energy growth as a function of initial conditions.

2. Backward-Facing Step Flow: This test case highlighted the method's effectiveness in handling two-dimensional flows. The data-driven approach yielded accurate transient growth predictions, using Hermite polynomials to significantly reduce the computational load compared to model-based methods.

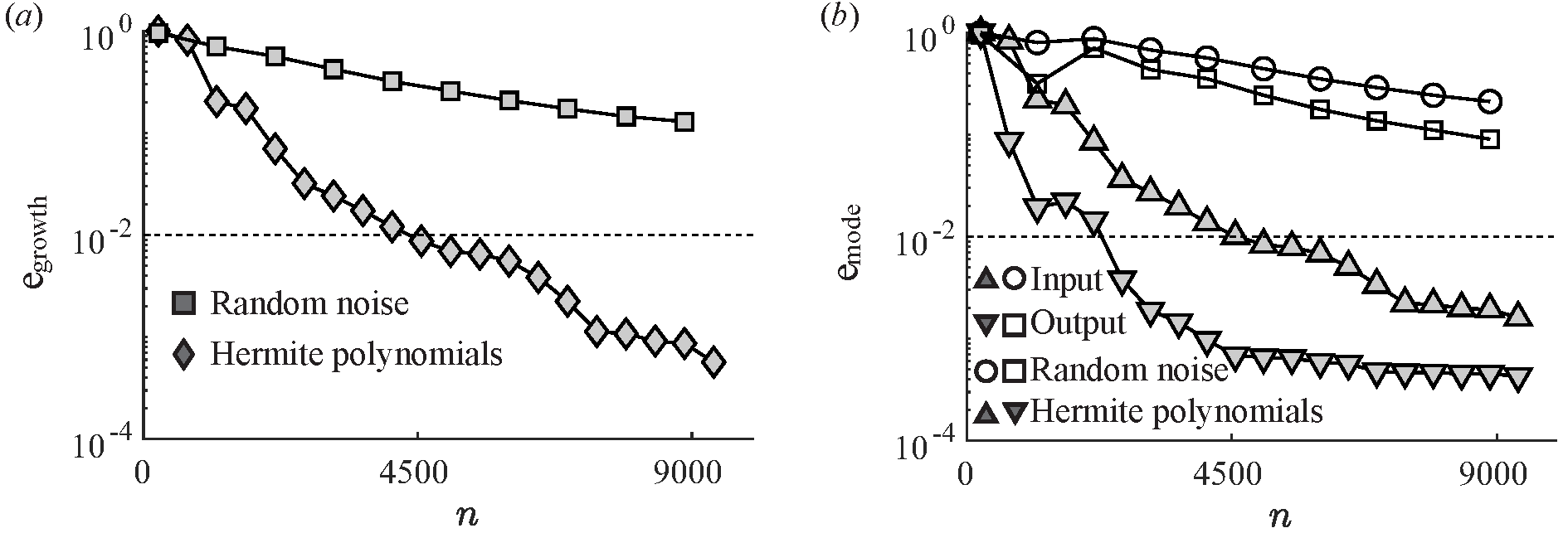
   Figure 2: Comparison of data-driven transient growth analyses of the backward-facing step flow using datasets obtained from LNS initialised with random noise and Hermite polynomials.

3. Batchelor Vortex: Demonstrating the method's applicability to three-dimensional flows, the algorithm accurately predicted transient growth rates and captured the optimal modes. The results were consistent even for configurations with higher complexity and dimensions.

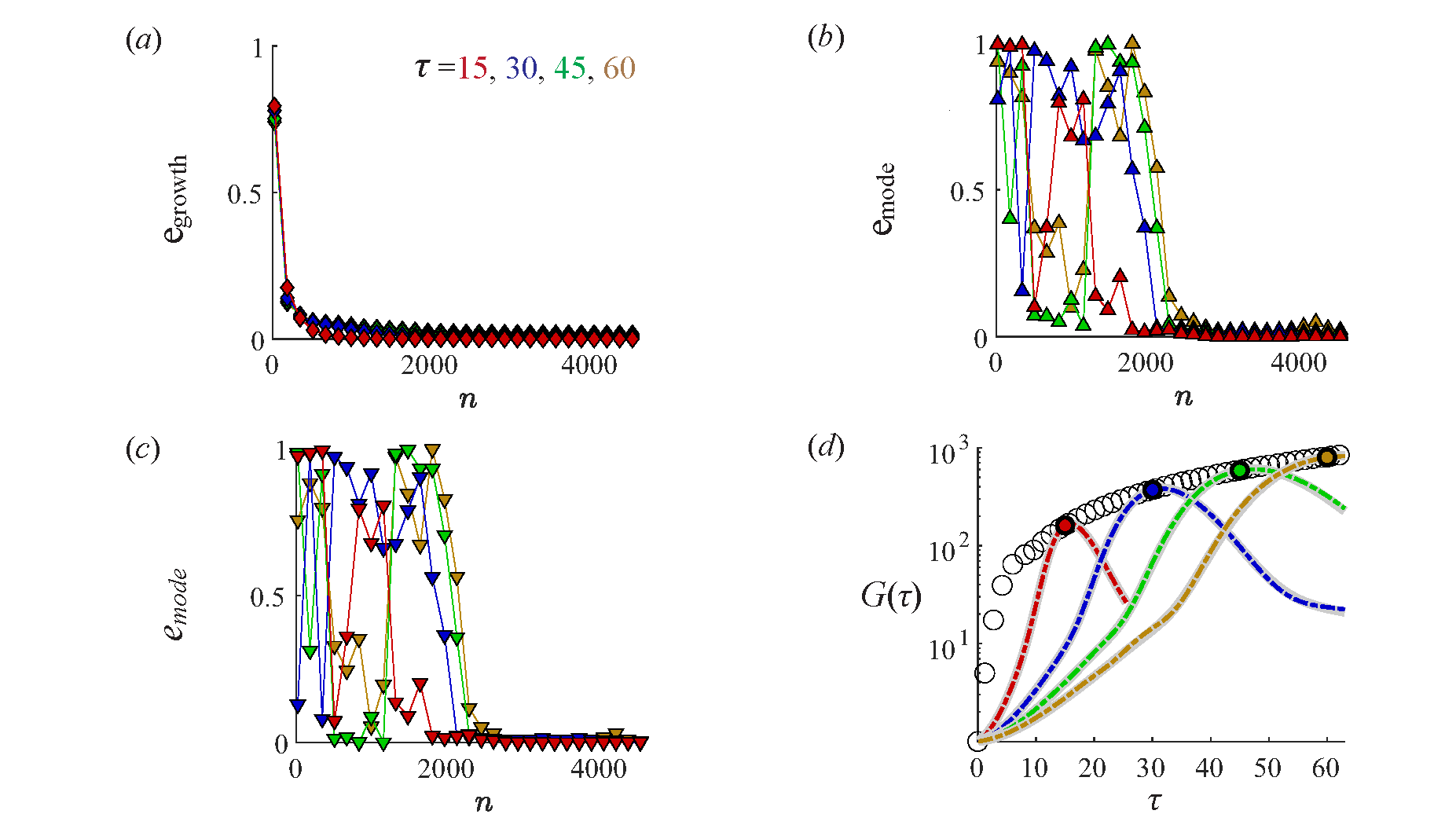
   Figure 3: Data-driven transient growth analysis of the axially decomposed Batchelor vortex at Re=1000.

Implications and Future Directions

The data-driven approach simplifies transient growth analysis by removing the need for developing and solving adjoint equations, thus making the process more accessible and less prone to computational errors. The successful application to varied fluid dynamics problems illustrates its versatility and potential for broader extensions in experimental settings.

The paper suggests future research could explore nonlinear applications and extend the methodology to handle compressible flow scenarios. There is also an opportunity to incorporate machine learning techniques to enhance the robustness and predictive capabilities of the data-driven framework.

Conclusion

This work presents a significant advancement in transient growth analysis, offering a more efficient and computationally feasible alternative to traditional methods. By leveraging data-driven principles, it holds promise for extensive applications across complex fluid dynamics contexts. The ability to perform such analyses without adjoint equations could democratize access to powerful analysis tools, fostering further developments in both theoretical and applied fluid mechanics.