Risk Comparisons in Linear Regression: Implicit Regularization Dominates Explicit Regularization (2509.17251v1)
Abstract: Existing theory suggests that for linear regression problems categorized by capacity and source conditions, gradient descent (GD) is always minimax optimal, while both ridge regression and online stochastic gradient descent (SGD) are polynomially suboptimal for certain categories of such problems. Moving beyond minimax theory, this work provides instance-wise comparisons of the finite-sample risks for these algorithms on any well-specified linear regression problem. Our analysis yields three key findings. First, GD dominates ridge regression: with comparable regularization, the excess risk of GD is always within a constant factor of ridge, but ridge can be polynomially worse even when tuned optimally. Second, GD is incomparable with SGD. While it is known that for certain problems GD can be polynomially better than SGD, the reverse is also true: we construct problems, inspired by benign overfitting theory, where optimally stopped GD is polynomially worse. Finally, GD dominates SGD for a significant subclass of problems -- those with fast and continuously decaying covariance spectra -- which includes all problems satisfying the standard capacity condition.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper asks a simple question: When you teach a computer to make predictions using a straight-line model (linear regression), which training method gives the most reliable results? The authors compare three popular ways to train such models:
- Gradient Descent (GD): slowly steps downhill on the error until you stop it early.
- Ridge Regression: adds a penalty to keep the model’s numbers small.
- Stochastic Gradient Descent (SGD): learns by looking at one example at a time, with steps that get smaller over time.
Their main message: the way GD naturally behaves (“implicit regularization”) often beats adding an explicit penalty (ridge). GD versus SGD is more complicated: sometimes GD wins, sometimes SGD wins—but for many common kinds of data, GD wins there too.
Goals and Questions
The paper focuses on these easy-to-understand goals:
- Compare how much extra prediction error (“excess risk”) each method has on the same problem.
- Ask: Is GD always at least as good as ridge regression? When does GD do better than SGD, and when worse?
- Understand these comparisons not just in worst-case theory, but on specific problems (instance-wise), using realistic assumptions about data.
How They Studied It (Methods in Plain Language)
Think of training as balancing two forces:
- Bias: how much the model misses the true pattern because it’s kept too simple or stops too early.
- Variance: how much the model chases random noise in the data and overfits.
The paper uses math to split the error into bias and variance and then bounds each part. Here’s the everyday picture:
- Gradient Descent (GD): like walking downhill towards the best fit. If you stop early, you avoid overfitting. Stopping early acts like a “hidden” regularizer—this is implicit regularization.
- Ridge Regression: adds a visible penalty that discourages big numbers in the model. This is explicit regularization.
- Stochastic Gradient Descent (SGD): learns step by step from individual data points, with step sizes shrinking over time. The randomness helps it avoid getting stuck, but its one-pass nature limits how precisely it can fine-tune.
Key ideas the authors formalize:
- Effective regularization: In ridge, this is the penalty size. In GD, it’s tied to how early you stop (roughly, stopping earlier means stronger regularization).
- Effective dimension: Think of your features sorted by importance (biggest to smallest). The “effective dimension” is roughly how many features matter for the model at a given regularization strength.
- Spectrum of the data (covariance spectrum): a list of feature strengths from strongest to weakest. Fast, smooth decay means each next feature is meaningfully smaller than the previous. Slow or spiky decay means many features are weak in an uneven way.
The authors:
- Prove new upper bounds (guarantees) on GD’s error that match the structure of known ridge bounds.
- Prove new lower bounds for GD (showing its limits).
- Use known tight bounds for ridge and SGD.
- Compare all three by aligning their “effective regularization” and “effective dimension.”
Main Findings and Why They Matter
1) GD beats ridge regression (one-sided dominance)
- With comparable regularization (match ridge’s penalty to GD’s early stopping), GD’s error is never more than a constant times ridge’s error.
- In many problems, GD is not just a little better—it can be polynomially better (its error shrinks much faster as you get more data), even when ridge is tuned optimally.
- Why it matters: It supports the idea that the way we train (early stopping) can naturally regularize better than adding a penalty. This strengthens the case for GD as a default choice.
2) GD and SGD are incomparable overall
- It was known that sometimes GD is much better than SGD.
- The surprise: The authors construct natural examples (inspired by “benign overfitting”) where even well-tuned, early-stopped GD is polynomially worse than SGD.
- Why it matters: Don’t assume one method is always best. The data’s structure (how feature strengths decay) can flip the winner.
3) GD dominates SGD for a large, important subclass of problems
- If the feature strengths decay fast and smoothly (includes the well-known “power-law” or capacity-condition cases), GD is always at least as good as SGD up to a constant factor—and can again be polynomially better.
- Why it matters: Many real datasets fit this pattern. In these common cases, early-stopped GD is a safe, strong choice.
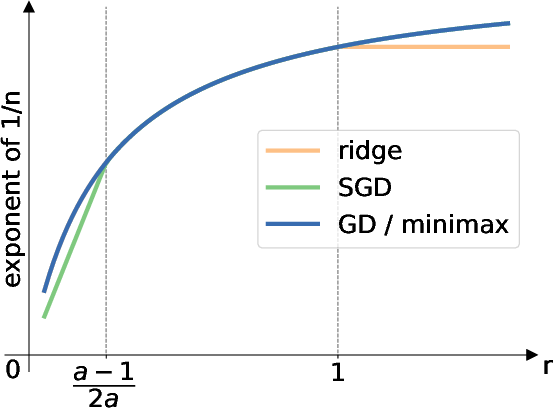
4) Minimax perspective (worst-case over a class of problems)
- For “power-law” problem classes (defined by how feature strengths and the true signal align), GD is minimax optimal for all settings they consider.
- Ridge and SGD are optimal only in limited ranges and can be polynomially suboptimal outside those ranges.
- Why it matters: GD’s training dynamics hit the best possible rates across broad conditions.
Implications and Impact
- Practical training advice: Early-stopped GD is a robust default. It’s at least as good as ridge in general, and often better. Against SGD, GD is the safer bet when your data’s feature strengths decay smoothly, which is common.
- Theory of generalization: This strengthens the “implicit regularization” story—how training dynamics alone (without added penalties) can keep models from overfitting, even in overparameterized settings.
- Algorithm choice: Don’t rely on one method for all problems. If your data suggests a slow, spiky spectrum (many weak but uneven features), consider SGD; otherwise, GD is often superior.
- Understanding “benign overfitting”: The paper connects when overfitting can still generalize well (benign overfitting) to cases where GD can struggle versus SGD, clarifying the boundary between batch (GD) and online (SGD) learning.
A Short Summary Table
The following short table summarizes the instance-wise comparisons the paper establishes:
| Comparison setting | Result |
|---|---|
| All well-specified linear regression problems | GD is always within a constant factor of ridge and can be much better; GD vs SGD is incomparable (each can win depending on data). |
| Problems with fast, smoothly decaying feature strengths (includes power-law/capacity condition) | GD dominates SGD (never worse up to a constant, sometimes much better). |
| Minimax over power-law classes | GD is minimax optimal for all source conditions; ridge and SGD only in limited ranges. |
In short: Early-stopped GD’s implicit regularization is surprisingly powerful—often stronger than adding penalties—and, in many common data settings, stronger than SGD too.
Knowledge Gaps
Unresolved gaps, limitations, and open questions
Below is a focused list of what remains missing, uncertain, or unexplored in the paper, stated concretely to guide future work.
- Relax the design assumptions: extend all comparisons and bounds beyond the independence and subgaussianity of the whitened covariates (entries of ), e.g., to dependent or elliptical designs, kernel-induced features with correlated coordinates, and heavy-tailed distributions.
- Bridge high-probability versus expectation gaps: provide matching expectation-level upper bounds for GD (not conditional on ) and high-probability lower bounds for ridge and SGD under the same assumptions, enabling fully apples-to-apples comparisons without invoking Bayesian symmetry.
- Remove (or weaken) the Bayesian symmetry requirement: establish GD’s dominance over ridge using only distributional symmetry of (or even weaker conditions), or entirely remove symmetry assumptions in lower bounds.
- Data-dependent tuning of GD: design stopping rules that are computable from data (e.g., using holdout/CV, discrepancy principles, or noise-level estimates) and achieve the proven instance-wise dominance over ridge and SGD without needing knowledge of , , , or .
- Dominance against optimally tuned baselines: strengthen “existence of ” results to show that a single data-driven GD stopping rule achieves a constant-factor risk of the best tuned ridge/SGD on every instance, uniformly over the problem class.
- Tighten the effective variance term for GD: prove (or refute) the conjectured improvement of the GD effective variance bound from to under general subgaussian designs; establish whether the term is information-theoretically necessary via lower bounds.
- Characterize the spectrum condition precisely: move beyond the sufficient “fast, continuously decaying spectrum” assumption to identify necessary and sufficient conditions on the covariance spectrum for GD to dominate SGD; delineate the exact boundary between dominance and incomparability.
- Robustness to SGD variants: extend incomparability and dominance results to commonly used SGD variants (mini-batch, multiple passes/epochs, constant stepsize with tail averaging, polynomial/exponential schedules, momentum/Nesterov, Adam-like methods); determine whether multi-pass SGD closes the gap with GD on the hard examples.
- Practical stepsize constraints: replace conditions like or with adaptive, data-driven stepsize selection strategies that retain the theoretical guarantees; analyze sensitivity to mis-specified stepsizes.
- Low-noise and noiseless regimes: rigorously identify the optimal (instance-wise and minimax) algorithms when is small or zero; quantify whether SGD, GD, OLS, or ridge (including negative regularization) is optimal and under what spectral/source conditions.
- Misspecified models and heteroskedastic noise: extend analyses to misspecification (), heteroskedastic or non-subgaussian noise, and label noise models; assess whether dominance relations persist or invert.
- Negative ridge regularization: compare GD to ridge with negative regularization (known to outperform OLS in certain regimes) and determine whether GD can match or dominate such explicitly regularized estimators.
- Computational budgets and multi-pass constraints: incorporate realistic compute constraints (number of passes/updates) into instance-wise comparisons to test whether GD’s “unlimited optimization power” is essential for dominance and how conclusions change under fixed compute.
- Constants and finite-sample calibration: make the hidden constants (, dependence on , , and ) explicit; quantify their magnitude and impact on finite-sample performance; provide guidance on when the constant-factor dominance is practically meaningful.
- Minimal dimension for separations: reduce the dimensionality requirement in the hard example () and characterize the minimal (as a function of , spectrum, and SNR) needed for a polynomial separation between GD and SGD.
- Unified GD analysis: develop a single bound that simultaneously recovers both the ridge-type and SGD-type behaviors of GD (across early and late stopping) without switching analytical techniques or assumptions.
- Extensions beyond linear regression: investigate whether analogous dominance/incomparability results hold for generalized linear models (e.g., logistic regression), non-quadratic losses, and non-convex models where GD’s implicit bias is known to prefer particular solutions.
- Kernel/functional settings without independence: adapt results to RKHS/kernel regression with general Mercer spectra where coordinates are not independent in any basis; clarify how the independence assumption interacts with infinite-dimensional settings.
- Empirical validation: provide controlled simulations and real-data experiments that (i) verify polynomial separations and dominance claims, (ii) assess sensitivity to design and noise assumptions, and (iii) test data-driven tuning procedures for GD, ridge, and SGD.
Practical Applications
Immediate Applications
Below are applications that can be deployed now, together with sectors, potential tools/workflows, and feasibility notes.
- AutoML default for linear regression: prefer gradient descent (GD) with early stopping over ridge regression when training offline
- Sector: software/ML platforms, data science teams
- Workflow/tool: “Ridge-to-GD tuner” that sets GD stopping time via the rule t ≈ 1/(η λ) to match a given ridge regularization λ, with a safe stepsize bound η ≤ 1/‖X Xᵀ‖ or η ≤ 1/(2 tr(Σ))
- Assumptions/dependencies: well-specified linear model; subgaussian features with approximately independent, normalized coordinates; bounded signal-to-noise ratio; ability to estimate tr(Σ) or ‖X Xᵀ‖
- Algorithm selection diagnostic based on spectrum decay
- Sector: finance (risk/factor models), healthcare (EHR prediction), marketing analytics (high-dimensional regression)
- Workflow/tool: “Spectrum Decay Estimator” that computes or approximates the leading eigenvalues of the sample covariance, tests for fast, continuous decay (e.g., polynomial/exponential), and recommends GD over SGD when the decay is fast and continuous
- Assumptions/dependencies: sufficient sample size for stable eigenvalue estimation; linearity approximation reasonable
- Early-stopping documentation for reproducibility and compliance
- Sector: policy/governance for ML, regulated industries (finance/healthcare)
- Workflow/tool: model cards/logs that record stepsize η and early stopping time t as the implicit ℓ2 regularization; use t ↔ λ mapping to justify regularization level equivalence between GD and ridge
- Assumptions/dependencies: consistent training protocol; stable η; governance processes recognize implicit regularization
- Risk budgeting in batch vs streaming regimes
- Sector: fintech (batch portfolio risk updates), healthcare (periodic risk scoring), IoT/edge (streaming signals)
- Workflow/tool: decision guide that recommends SGD for one-pass/streaming constraints and GD for multi-pass batch settings with fast spectral decay; include last-iterate SGD with exponentially decaying stepsize for streaming
- Assumptions/dependencies: operational constraints (one-pass vs multi-pass); spectral shape differs by domain (e.g., sensor streams may be heavy-tailed)
- Effective dimension diagnostics to avoid underperformance
- Sector: ML engineering, MLOps
- Workflow/tool: compute effective dimensions D and D₁ (using estimated eigenvalues, sample size n, and stepsize/stop-time) to anticipate variance terms; if D₁ ≫ D (heavy tails/spikes), prefer SGD or adjust GD schedule
- Assumptions/dependencies: access to sample covariance; accurate n and stepsize scheduling
- Benign overfitting alerts
- Sector: IoT/robotics, ad tech, genomics
- Workflow/tool: detector that flags slow-decaying or spiky spectra (conditions enabling benign overfitting) to warn that optimally stopped GD/OLS may be polynomially worse than SGD; suggests SGD with appropriate decay schedule
- Assumptions/dependencies: spectral estimate; alignment to linear regime; noise is well-specified
- Curriculum and training materials on implicit vs explicit regularization
- Sector: academia, corporate training
- Workflow/tool: teaching modules showing GD’s implicit ℓ2 regularization, the t ↔ λ mapping, and when GD dominates ridge or SGD
- Assumptions/dependencies: pedagogical use; access to synthetic datasets illustrating spectral regimes
- Pipeline modernization: replace ridge with early-stopped GD in high-dimensional tabular modeling when spectrum decays fast
- Sector: healthcare (lab results, claims), energy (load forecasting), retail (SKU demand modeling)
- Workflow/tool: swap ridge solvers with GD + early stopping; validate using risk bounds and hold-out sets; use conservative stepsize schedule and t ≤ b n
- Assumptions/dependencies: fast, continuous spectral decay; data preprocessing maintains subgaussian behavior
- Streaming-friendly optimizer setup for last-iterate SGD
- Sector: mobile/edge analytics, large-scale ad platforms
- Workflow/tool: implement last-iterate SGD with exponentially decaying stepsize (per paper’s schedule); prefer SGD when optimization budget limits batch passes or spectrum is not fast-decaying
- Assumptions/dependencies: constrained I/O; stable step scheduler; monitoring of N = n/log n for effective regularization
Long-Term Applications
These applications require further research, scaling, or development before deployment.
- Adaptive optimizer that switches between GD and SGD based on online spectrum estimates
- Sector: ML platforms, MLOps
- Product/workflow: “Adaptive Optimizer” that estimates k*, D, D₁ on the fly and chooses GD (early stopping) or SGD (decay schedule) per minibatch/session
- Assumptions/dependencies: streaming spectral estimation; robust, low-overhead eigenvalue tracking; extension beyond linear models
- Extensions beyond linear regression to generalized linear models and deep nets
- Sector: software/ML research, applied AI
- Workflow/tool: investigate whether GD’s implicit regularization dominance over explicit ℓ2 holds under logistic/Poisson regression and in deep architectures; derive analogous bounds and schedules
- Assumptions/dependencies: theory development; possible relaxation of subgaussian and independence assumptions
- Robust spectral estimation under dependence and heavy tails
- Sector: finance (dependent factors), sensor networks (correlated signals)
- Workflow/tool: randomized trace/eigenvalue estimators resilient to correlation and non-subgaussian tails; confidence intervals for decay classification
- Assumptions/dependencies: algorithmic advances in robust covariance estimation; scalable implementations
- Hybrid batch–stochastic regression methods
- Sector: large-scale ML systems
- Product/workflow: “Hybrid Batch-Stochastic Regression” that warms up with early-stopped GD to reduce bias then switches to SGD to control variance in heavy-tail regimes; schedules derived from effective dimension estimates
- Assumptions/dependencies: orchestration across passes; harmonized learning rate and stop-time policies
- Standards and guidelines for implicit regularization in regulated ML
- Sector: policy and governance
- Workflow/tool: formal guidance recommending early stopping as a bounded-risk alternative to explicit ridge, with spectrum-based exceptions where SGD is preferable; documentation standards for η and t
- Assumptions/dependencies: multi-stakeholder consensus; alignment with auditing frameworks
- Energy- and hardware-aware training policies
- Sector: energy, cloud/edge compute
- Workflow/tool: optimize “generalization per joule” by favoring GD in fast-decay spectra (fewer passes with early stopping) and SGD in streaming/heavy-tail settings; integrate with scheduler and resource manager
- Assumptions/dependencies: accurate power/performance models; workload characterization
- Algorithms for noiseless/low-noise regimes superior to OLS/GD
- Sector: genomics, scientific computing, high-precision measurements
- Workflow/tool: leverage insights that SGD can outperform OLS/GD in high-dimensional noiseless settings to design tailored procedures (e.g., SGD with specific decay schedules or regularized pseudoinverse variants)
- Assumptions/dependencies: problem structure (spiky/slow-decay spectra); careful step scheduling and stability analysis
- Library support for effective-regularization diagnostics
- Sector: open-source ML ecosystems (e.g., scikit-learn, PyTorch)
- Product/workflow: standardized functions to compute k*, D, D₁, and map between λ and t; APIs that expose implicit/explicit regularization equivalence and spectral-based optimizer recommendations
- Assumptions/dependencies: access to sample covariance; efficient numerical routines; community adoption
Notes on feasibility across items:
- Many results assume well-specified linear regression, subgaussian features with independent normalized entries, and bounded signal-to-noise. Real-world data may violate these; diagnostics and robust estimators are needed.
- Spectrum-based recommendations depend on reliable eigenvalue estimation, which can be challenging in small n or highly noisy settings.
- Stepsize bounds (e.g., η ≤ 1/(2 tr(Σ))) and early stopping t ≤ b n are important for the GD bounds; operational pipelines must enforce these constraints.
Glossary
- Anisotropic prior: A non-isotropic (direction-dependent) prior distribution over parameters. "when considering anisotropic priors, there exist examples such that GD is polynomially better than ridge regression"
- Batch learning: Learning from the entire dataset at once as opposed to sequentially. "revealing an unexpected separation between batch and online learning."
- Bayes optimal: The estimator that minimizes expected risk under a given prior. "ridge regression with optimally tuned regularization is well-known to be Bayes optimal."
- Bayesian symmetry: A symmetry assumption on the prior of the optimal parameter that simplifies analysis. "Bayesian symmetry"
- Benign overfitting: The phenomenon where overparameterized models interpolate data yet generalize well. "enables the surprising phenomenon of benign overfitting"
- Bias and variance decomposition: Splitting prediction error into bias and variance components. "enables a tight bias and variance decomposition."
- Bias error: The component of excess risk due to systematic estimation error. "the bias error (the terms involving $\wB^*$)"
- Bias-variance tradeoff: The balance between bias and variance to minimize overall error. "effective regularization, controlling the bias-variance tradeoff."
- Capacity and source conditions: Spectral and smoothness assumptions that characterize problem difficulty. "categorized by capacity and source conditions"
- Capacity condition: A condition on the decay of the covariance spectrum (e.g., power-law). "power-law spectra (also known as the capacity condition)"
- Convex smooth problem: An optimization problem with convex objective and Lipschitz-continuous gradients. "for every convex smooth problem"
- Covariance spectra: The set of eigenvalues of the covariance operator, describing feature variance. "fast and continuously decaying covariance spectra"
- Critical index: A threshold index determining head/tail splits in spectral analyses. "the critical index "
- Effective bias error: The portion of bias error after accounting for algorithmic regularization effects. "an effective bias error"
- Effective dimension: A data-dependent measure of complexity capturing the contribution of spectral tail. "effective dimension "
- Effective regularization: The implicit or explicit parameter controlling bias-variance tradeoff. "effective regularization, controlling the bias-variance tradeoff."
- Effective variance error: Additional variance component induced by early stopping or algorithm dynamics. "an effective variance error"
- Eigendecomposition: Representation of a symmetric operator via its eigenvalues and eigenvectors. "Let the eigendecomposition of the covariance $\SigmaB\in\Hbb^{\otimes 2}$ be"
- Empirical risk minimizer: The parameter that minimizes average training loss. "GD converges to the empirical risk minimizer with minimum -norm."
- Explicit regularization: Direct penalization (e.g., norm penalties) added to the loss. "in the absence of explicit regularization"
- Expectation lower bound: A lower bound on risk that holds in expectation over randomness. "The expectation lower bound is by \citet[Theorem B.2]{zou2021benefits}"
- Excess risk: The difference between the risk of an estimator and the optimal risk. "the excess risk of GD is always within a constant factor of ridge"
- Finite-sample risks: Risk evaluations that account for limited sample sizes. "instance-wise comparisons of the finite-sample risks"
- Gaussian design: Assumption that features are drawn from a Gaussian distribution. "Gaussian design allows us to prove a stronger concentration bound"
- Gaussian linear regression problems: Linear regression with Gaussian features and noise. "Gaussian linear regression problems satisfy \Cref{assum:upper-bound,assum:lower-bound} with "
- Gradient flow: The continuous-time limit of gradient descent dynamics. "one can consider gradient flow (by taking and rescaling the stopping time accordingly)"
- High probability lower bound: A lower bound that holds with probability close to one. "the upper bound and the high probability lower bound are due to \citet{tsigler2023benign}"
- Hilbert space: A complete inner-product space generalizing Euclidean space to infinite dimensions. "Let $\Hbb$ be a separable Hilbert space."
- Implicit regularization: Regularization effects induced by the optimization algorithm rather than explicit penalties. "The implicit regularization of GD is tightly connected to an explicit norm regularization."
- Instance-wise risk comparisons: Comparing algorithms’ risks on each individual problem instance. "Instance-wise risk comparisons (Table~\ref{tab:comparison):}"
- Isotropic prior: A prior distribution that is rotationally symmetric across directions. "assuming the optimal parameter $\wB^*$ satisfies an isotropic prior"
- Last iterate: The final parameter produced by an iterative optimization algorithm. "We focus on the last iterate of SGD"
- Maximum -margin: The largest margin in feature space under the Euclidean norm. "GD converges in direction to the maximum -margin parameter vector"
- Minimax optimal regime: Parameter ranges where an algorithm achieves the minimax optimal rate. "minimax optimal regime"
- Minimax optimality: Achieving the best worst-case rate over a class of problems. "Minimax optimality (Table~\ref{tab:minimax):}"
- Minimax theory: Statistical framework focusing on worst-case performance over function classes. "Moving beyond minimax theory"
- Online stochastic gradient descent (SGD): SGD applied in streaming or single-pass fashion over data. "online stochastic gradient descent (SGD)"
- Operator methods: Analytical techniques leveraging linear operators to paper algorithm dynamics. "build upon the operator methods developed by \citet{zou2023benign}"
- Operator norm: The largest singular value (or eigenvalue for symmetric operators) of a matrix/operator. "we write $\|\MB\|$ as its operator norm, i.e., its largest eigenvalue."
- Order-1 effective dimension: A variant of effective dimension scaling linearly with spectral tail sums. "order-$1$ effective dimension "
- Ordinary least squares (OLS): The unregularized linear regression estimator minimizing squared error. "ordinary least squares (OLS, i.e., ridge regression with )"
- Overparameterized: Having more parameters than training samples. "overparameterized linear regression"
- Polylogarithmic factors: Multiplicative terms that are polynomial in logarithms of sample size. "hide polylogarithmic factors within the $\Ocal$ and notation"
- Positive semi-definite (PSD): A matrix/operator whose quadratic form is nonnegative for all vectors. "For a positive semi-definite (PSD) matrix $\MB$"
- Power-law problem class: A class where spectral decay follows a power law, used for rate analysis. "power-law problem class"
- Pseudoinverse: Generalized inverse of a possibly singular matrix. "we define $\MB^{-1}$ as its pseudoinverse."
- Population probability measure: The underlying distribution generating feature-response pairs. "associated with a population probability measure $\mu(\xB, y)$"
- Population risk: Expected squared loss over the data-generating distribution. "we seek to minimize the population risk"
- Ridge regression: Linear regression with -norm regularization. "Ridge regression produces the -regularized empirical risk minimizer"
- Ridge-type upper bound: An upper bound for GD shaped like ridge regression bounds. "a ridge-type upper bound for GD"
- Separable Hilbert space: A Hilbert space with a countable dense subset. "Let $\Hbb$ be a separable Hilbert space."
- Signal-to-noise ratio: The relative magnitude of signal power to noise variance. "provided that the signal-to-noise ratio is bounded from above"
- Source condition: Smoothness of the true parameter relative to the covariance operator. "source conditions "
- Stochastic averaging: Implicit regularization arising from averaging stochastic updates. "stochastic averaging \citep{polyak1992acceleration}"
- Stopping time: The iteration count at which training is halted (for early stopping). "the stopping time for GD is set inversely proportional to the ridge regularization"
- Subgaussian: A tail behavior class with exponential concentration similar to Gaussian distributions. "the entries of $\SigmaB^{-\frac{1}{2}\xB$ are independent and -subgaussian;"
- Tail iterates: Iterations near the end of an optimization run, often averaged in SGD. "the average of the tail iterates of SGD"
- Trace: The sum of diagonal entries (or eigenvalues) of a matrix/operator. "assume the trace and all entries of $\SigmaB$ are finite."
- Variance error: The component of excess risk due to randomness/noise. "the variance error (the terms involving )"
- Well-conditioned problems: Problems with favorable spectral properties (e.g., larger smallest eigenvalues). "well-conditioned problems"
- Well-specified linear regression: A setting where the linear model correctly captures the conditional mean. "well-specified linear regression"
Collections
Sign up for free to add this paper to one or more collections.