Pre-training under infinite compute (2509.14786v1)
Abstract: Since compute grows much faster than web text available for LLM pre-training, we ask how one should approach pre-training under fixed data and no compute constraints. We first show that existing data-constrained approaches of increasing epoch count and parameter count eventually overfit, and we significantly improve upon such recipes by properly tuning regularization, finding that the optimal weight decay is $30\times$ larger than standard practice. Since our regularized recipe monotonically decreases loss following a simple power law in parameter count, we estimate its best possible performance via the asymptote of its scaling law rather than the performance at a fixed compute budget. We then identify that ensembling independently trained models achieves a significantly lower loss asymptote than the regularized recipe. Our best intervention combining epoching, regularization, parameter scaling, and ensemble scaling achieves an asymptote at 200M tokens using $5.17\times$ less data than our baseline, and our data scaling laws predict that this improvement persists at higher token budgets. We find that our data efficiency gains can be realized at much smaller parameter counts as we can distill an ensemble into a student model that is 8$\times$ smaller and retains $83\%$ of the ensembling benefit. Finally, our interventions designed for validation loss generalize to downstream benchmarks, achieving a $9\%$ improvement for pre-training evals and a $17.5\times$ data efficiency improvement over continued pre-training on math mid-training data. Our results show that simple algorithmic improvements can enable significantly more data-efficient pre-training in a compute-rich future.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks a simple but important question: What should we do if we have tons of computer power to train AI, but not much new text to train on? The authors paper how to pre-train LLMs when data is limited but compute is (almost) unlimited. They test different ways to squeeze more learning out of the same data without overfitting.
What questions did the researchers ask?
In plain terms, they asked:
- If we can’t get much more text, how can we keep improving LLMs?
- Is it better to make one giant model, or to train many smaller models and combine them?
- How should we set training knobs (like how many times we re-read the same data and how strong we regularize) to avoid overfitting?
- Can we compress the power of many models into one small model (so it’s cheap to use) without losing much quality?
- Do these improvements show up on real tasks, not just on a training score?
How did they paper it?
Think of training as studying from a textbook (the data) using a computer. Here’s their setup explained simply:
- Limited textbook: They fixed a small “book” of 200 million tokens (tokens are pieces of words) to simulate a future where data grows slowly.
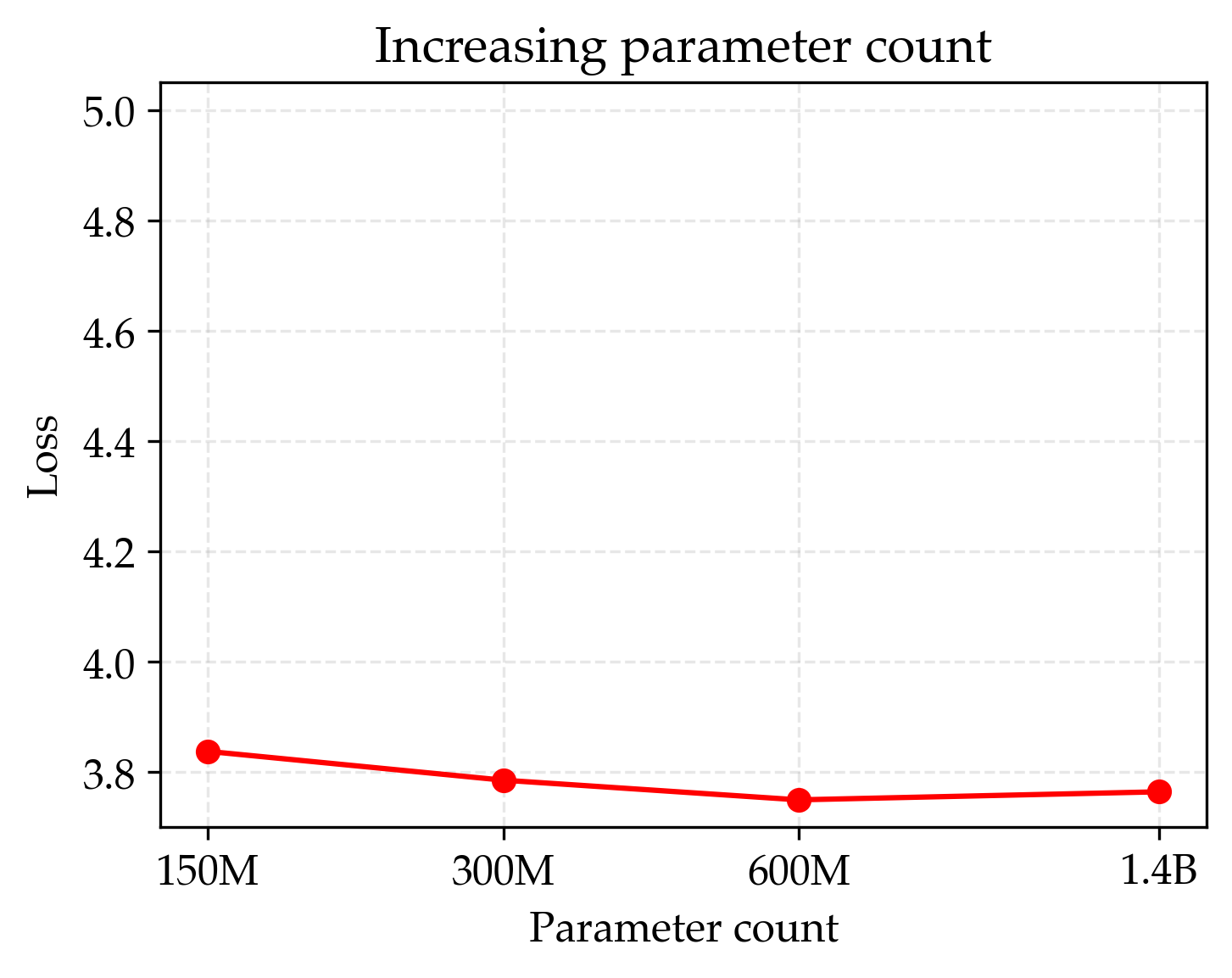
- Unlimited paper time: They allowed themselves lots of compute (as if they could paper that same book as long as they wanted).
- Two main paper strategies: 1) Standard approach: Make models bigger and/or re-read the same data many times (more “epochs”). This often leads to overfitting—like memorizing the answers instead of understanding. 2) Regularized approach: Add strong regularization (especially “weight decay,” which is like a penalty for memorizing) and carefully tune training settings so the model generalizes better.
- Teamwork strategy (ensembling): Train several small models independently and average their predictions, like asking a panel of tutors and taking their consensus.
- Measuring progress: They used “loss” as the main score—lower is better. You can think of loss as: How wrong is the model on new, unseen text?
- Looking for the “best you can possibly do”: Instead of asking “What’s best at a fixed budget?” they asked, “If you keep scaling a strategy up, what score will it approach?” That long-run ceiling is called its “asymptote.”
- Compression (distillation): After training a powerful team (an ensemble), they trained a single smaller student to imitate the team, so it’s fast and cheap at use time.
- Broader checks: They also tested the models on beginner-friendly benchmarks (PIQA, SciQ, ARC Easy) and on continued pre-training for math data to see if the gains carry over.
Technical terms in everyday language:
- Epoch: Re-reading the same book again.
- Overfitting: Memorizing the book’s exact sentences, so you struggle with new questions.
- Regularization/weight decay: Training rules that discourage memorization and encourage learning patterns; like a teacher who penalizes “rote copying.”
- Ensemble: Many students solve the same problem, and you average their answers.
- Distillation: The many students teach one new student, so the single student captures most of the group’s wisdom.
- Power law and asymptote: As you invest more, you keep improving but with diminishing returns. The asymptote is the best score you can get if you keep going forever.
What did they find?
Here are the key results, with a brief explanation of why they matter:
- Standard recipe overfits with limited data
- Just making models bigger or re-reading the data too many times eventually made performance worse (loss went up). So the usual “just scale up” playbook fails when data is the bottleneck.
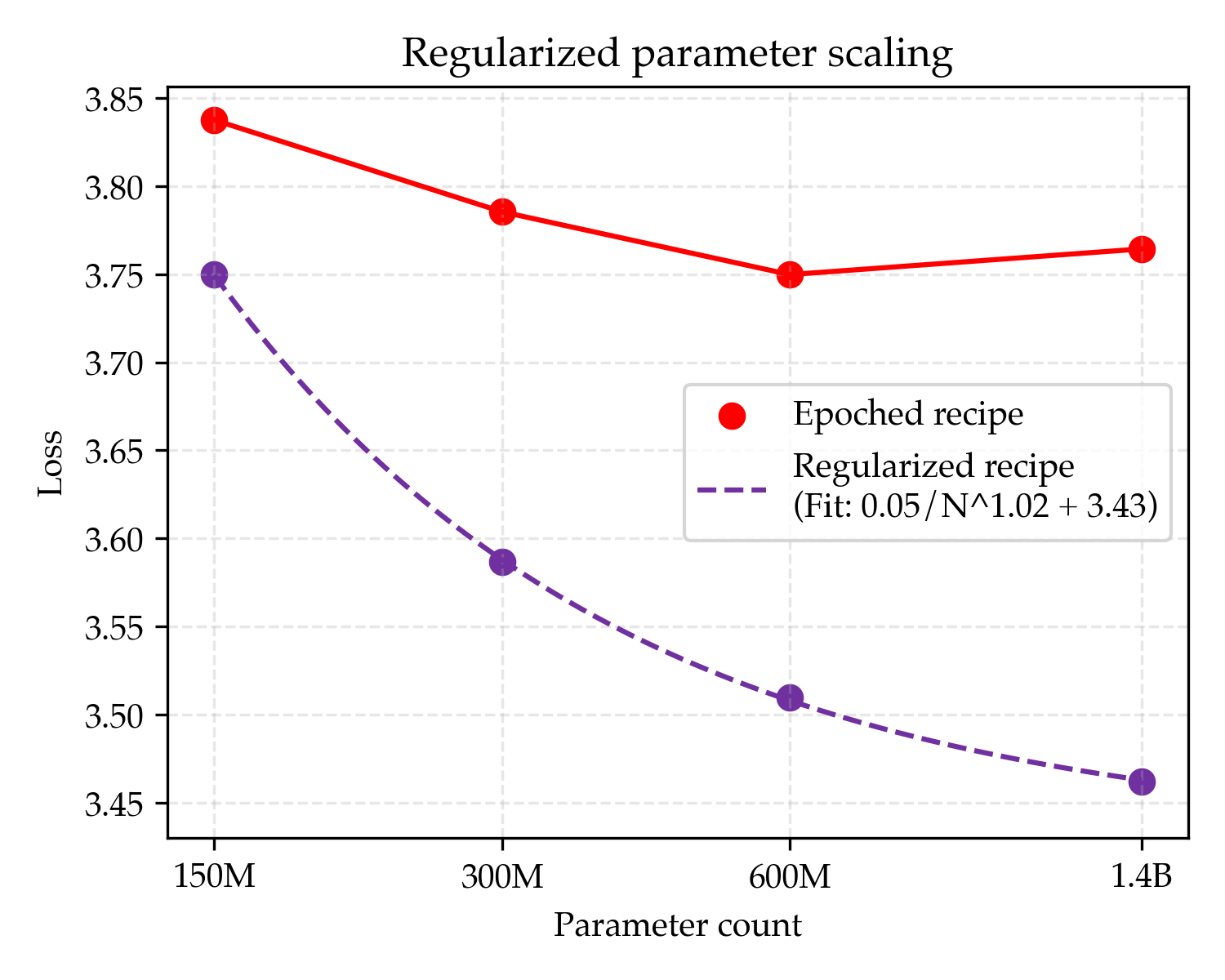
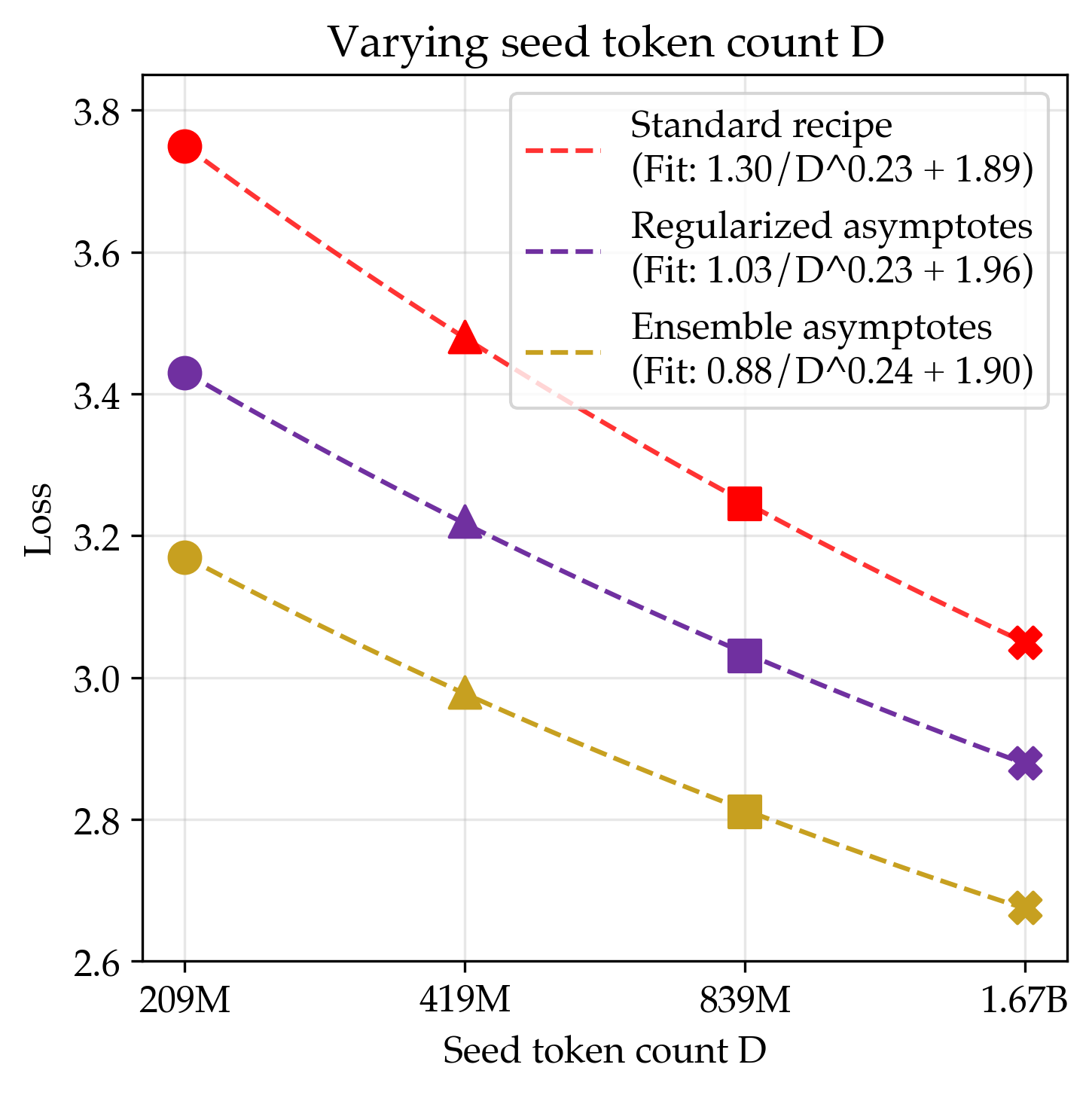
- Strong regularization fixes overfitting and brings smooth gains
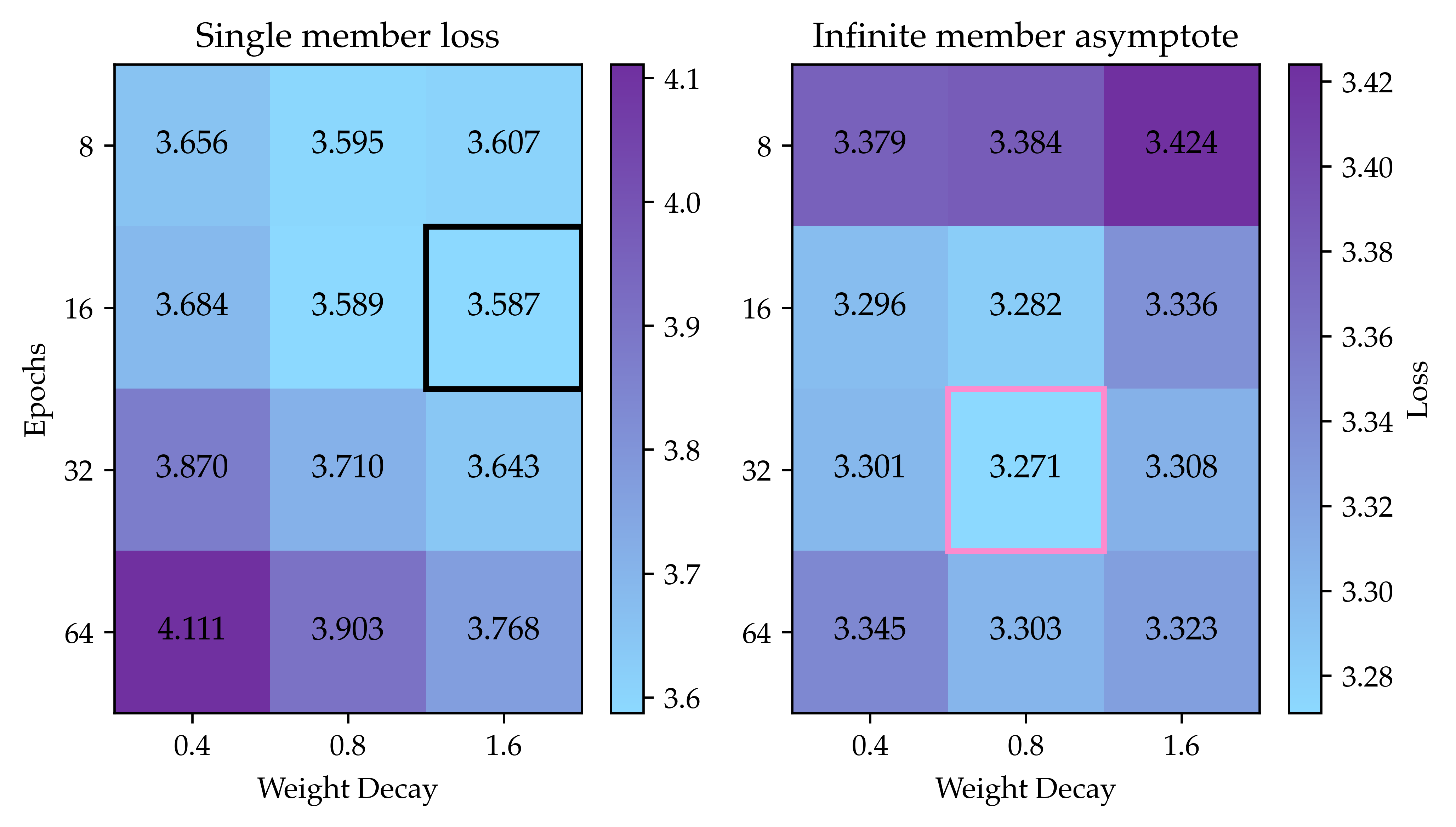
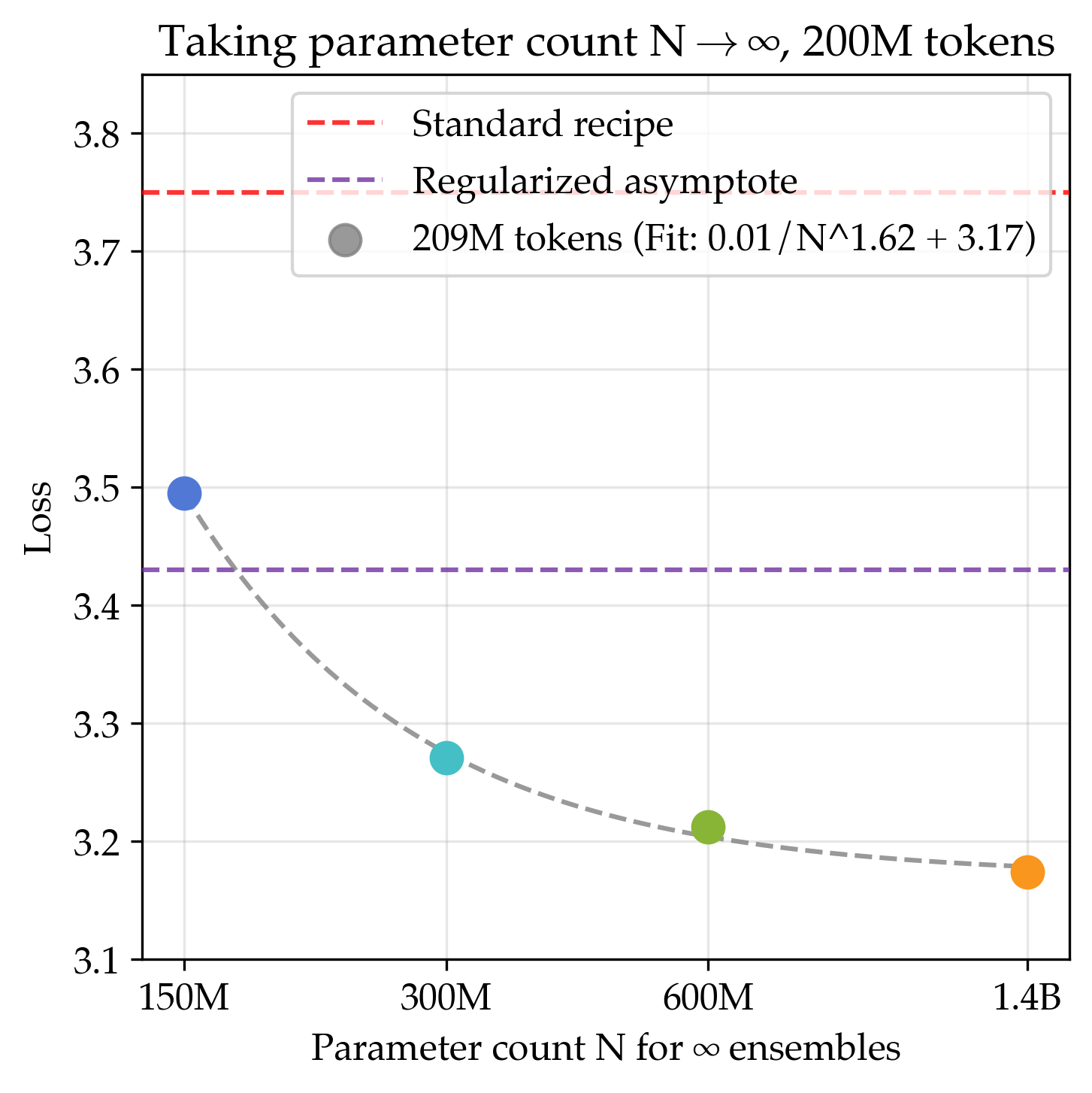
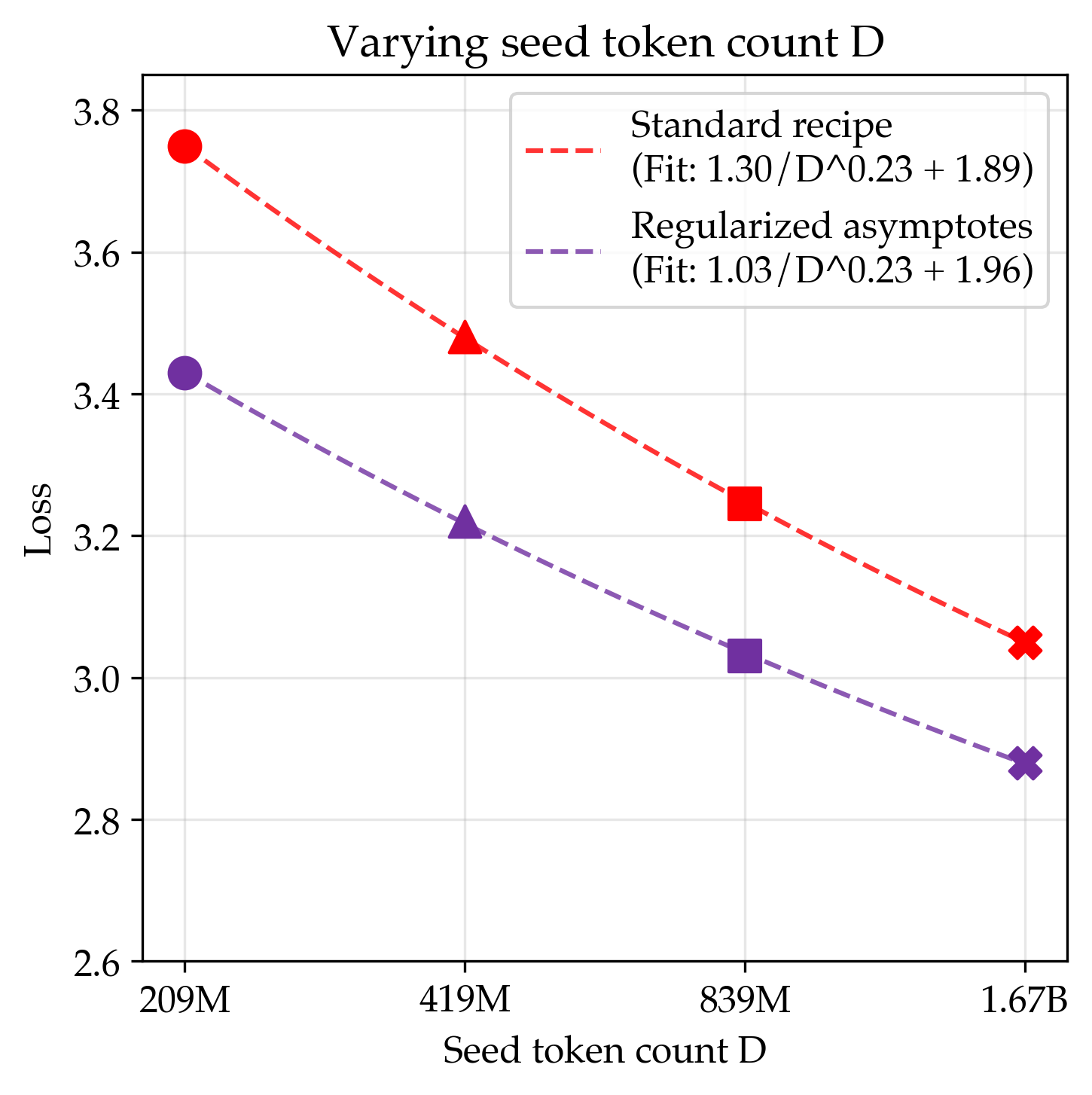
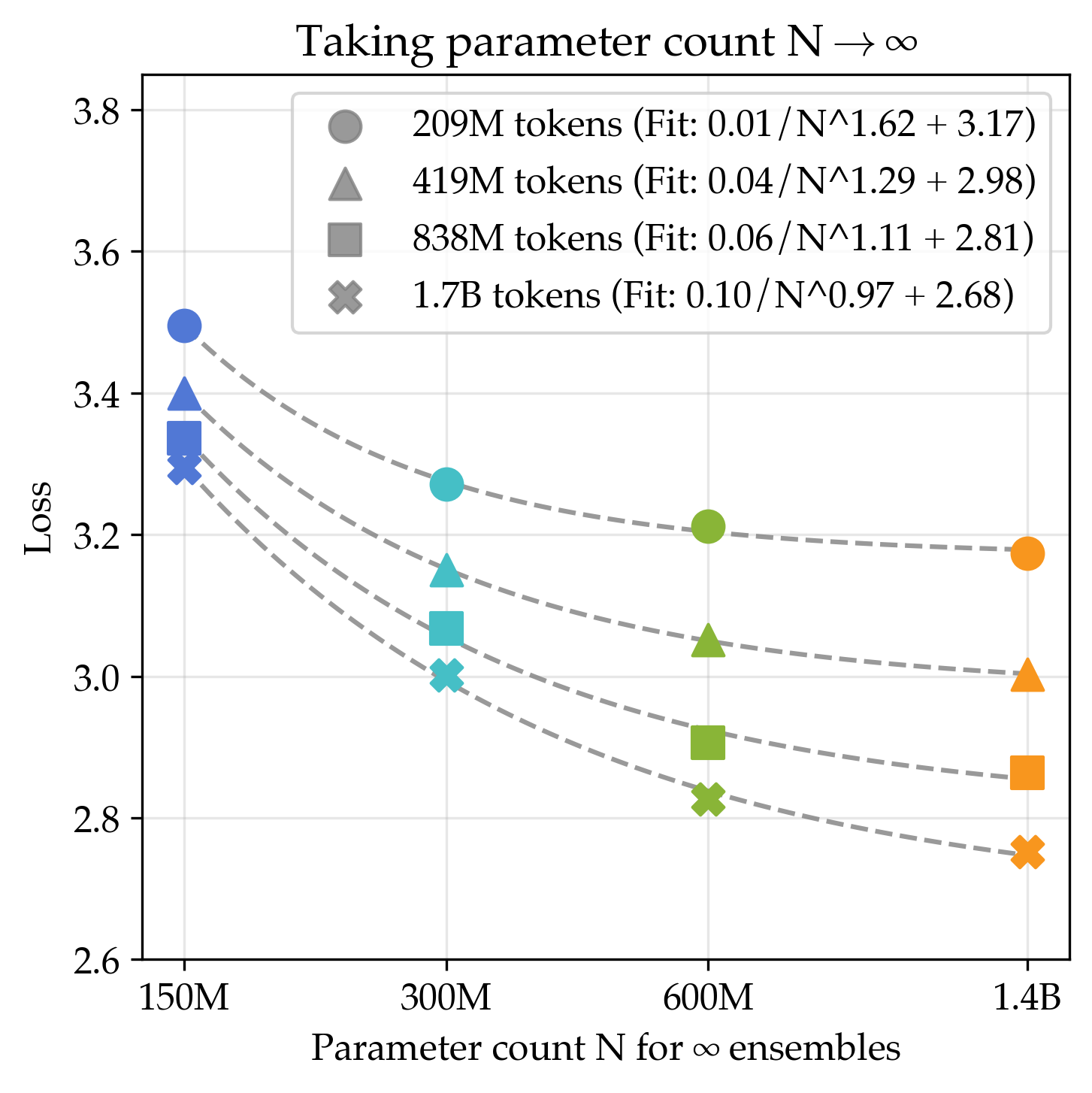
- By tuning training more carefully—especially using much stronger weight decay (around 30× the common default)—they got steady improvements as models grew. Their long-run best score (asymptote) for this “regularized” recipe was better than the standard one.
- Translation: With the right guardrails, bigger models do help even with limited data.
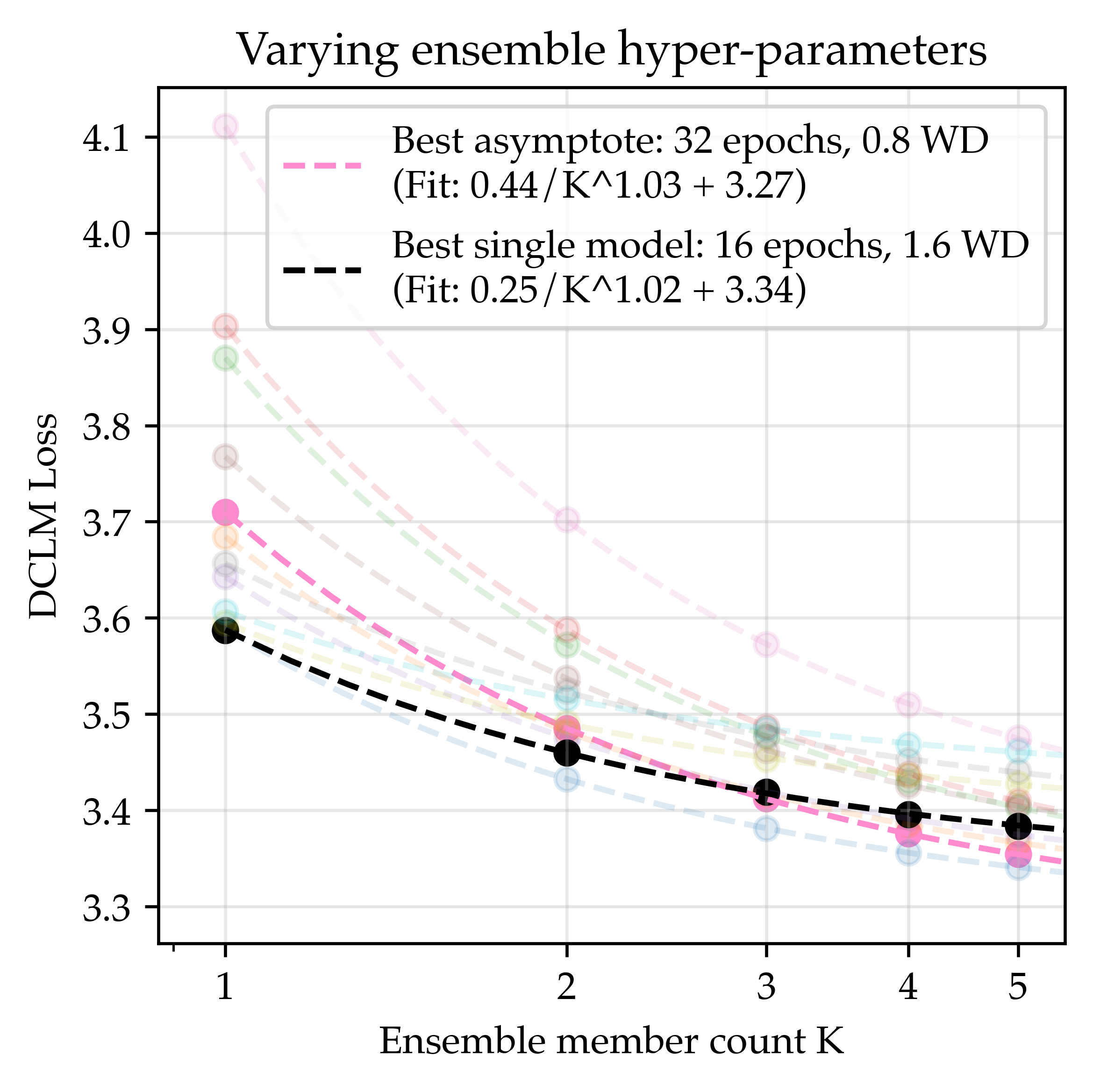
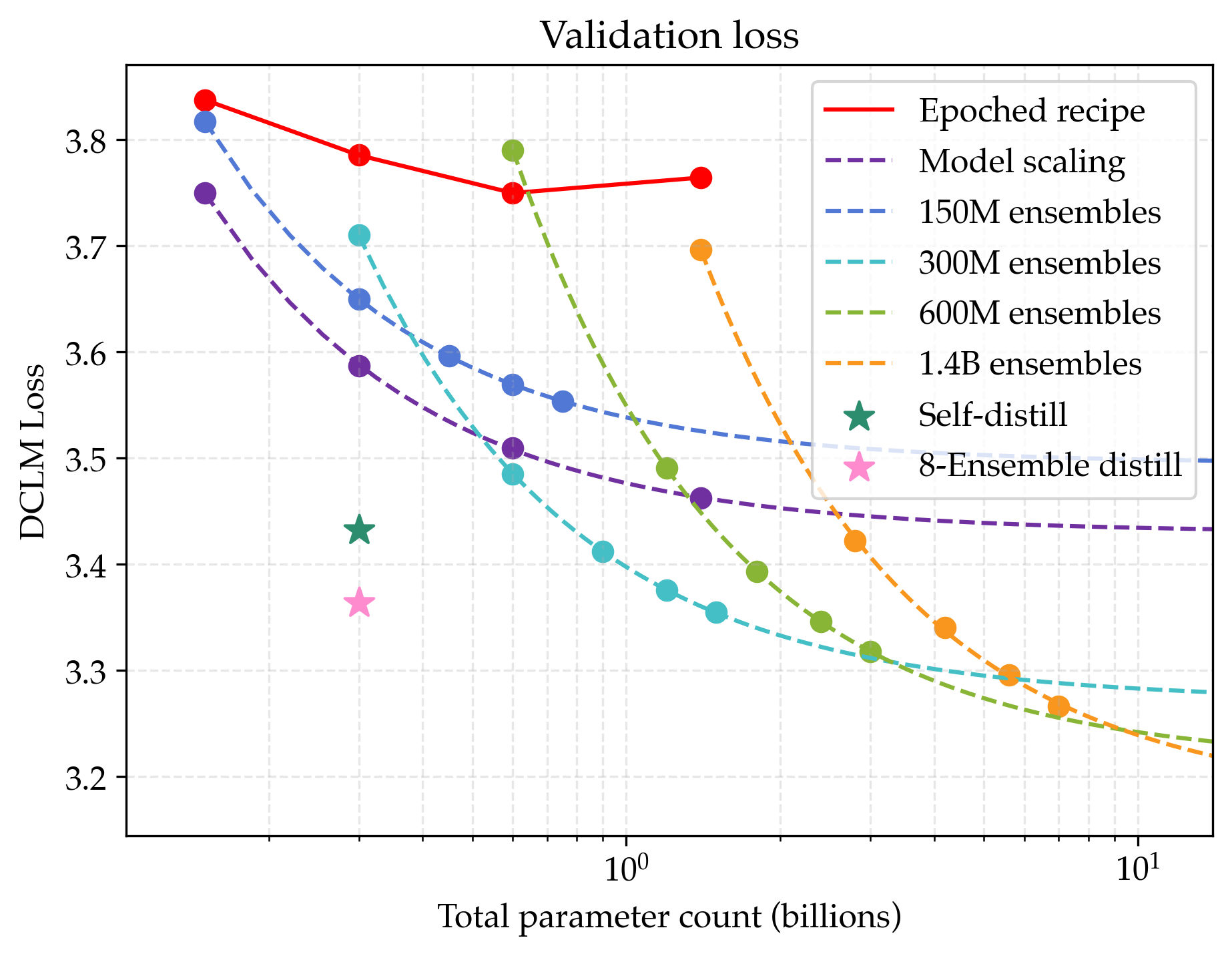
- Teams of small models (ensembles) beat single huge models
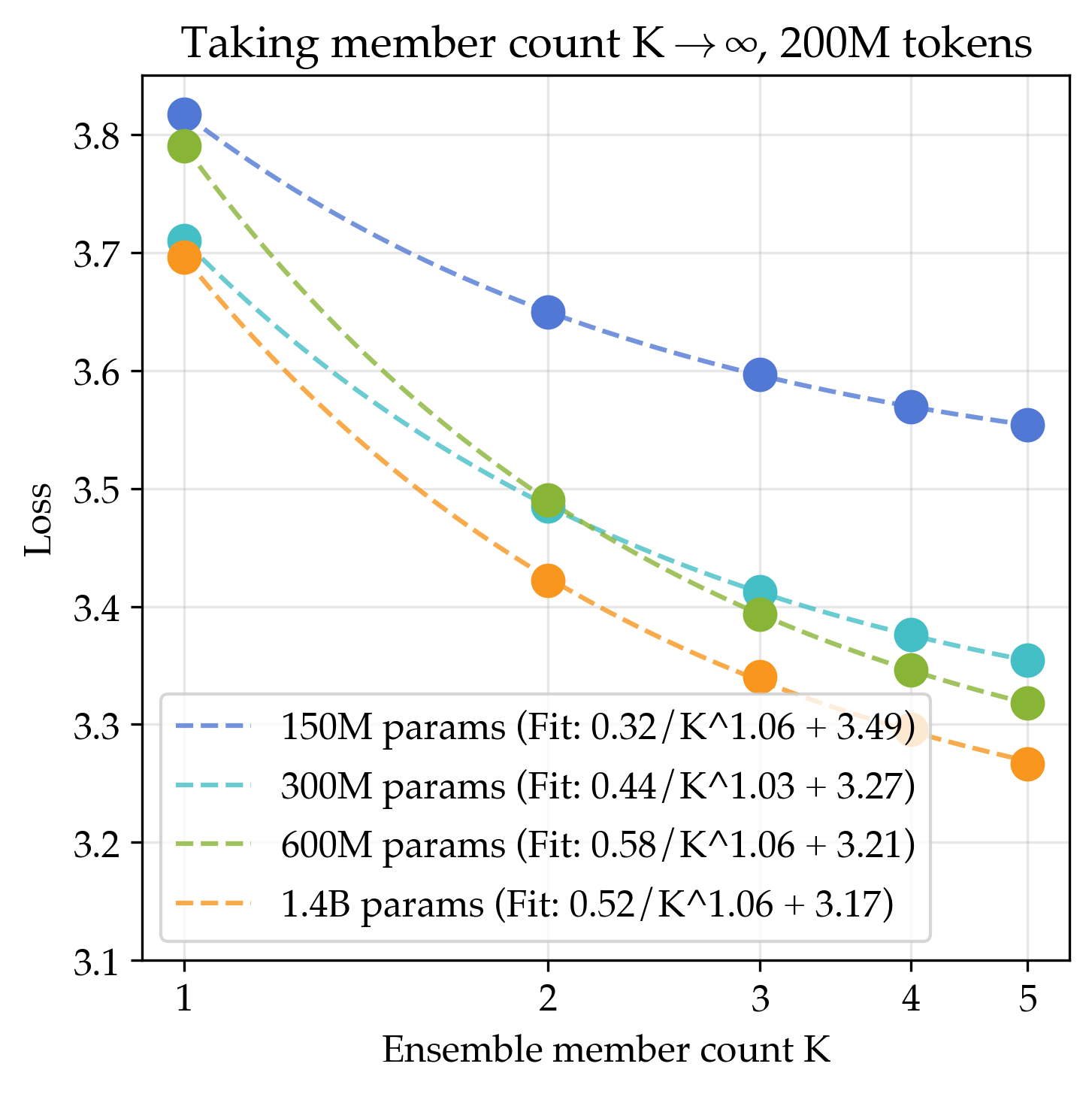
- Averaging the outputs of many small models gave a lower best-possible score than making a single model arbitrarily large. Even a 3-model ensemble beat what a single huge model could reach in the long run.
- Why this works: Different models latch onto different “views” or patterns in the data; combining them covers more ground.
- Combining both ideas is best
- If you both increase model size and increase the number of models in the ensemble, the long-run best score improves even more.
- Data efficiency gains: At 200M tokens, this joint strategy was about 5.17× more data efficient than the standard recipe. That means to match its performance, the standard method would need over five times more data.
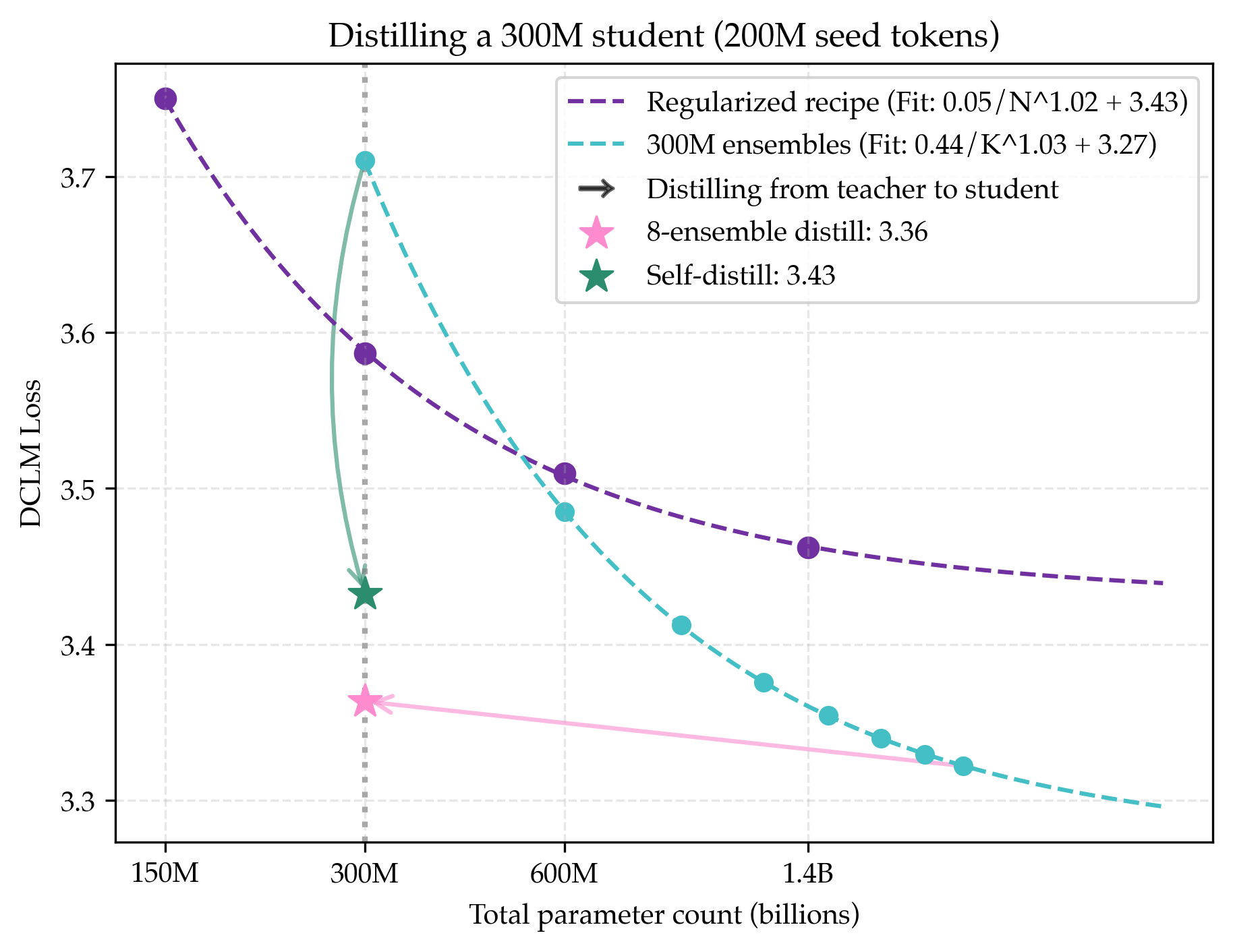
- You can compress the team into one small model (distillation) and keep most gains
- Distilling an 8-model ensemble into a single 300M-parameter model kept about 83% of the ensemble’s improvement. So you can train with many models but deploy just one—cheap and fast.
- Self-distillation (same-size teacher and student) surprisingly helps
- Training a new 300M model on a mix of real data and synthetic data generated by a previous 300M model produced a better 300M model than before—without ever training a larger model. This avoids “model collapse” by mixing real and synthetic data.
- The gains show up on real tasks
- On beginner-friendly benchmarks (PIQA, SciQ, ARC Easy), the models with better loss also performed better. Their best ensemble beat the best unregularized model by about 9% on average.
- It also boosts continued pre-training (CPT) on math data
- Using just 4B tokens and ensembling epoched models, they beat a baseline that used the full 73B tokens—a roughly 17.5× data efficiency improvement.
Why does this matter?
- The future will likely have less new clean data but more compute. This paper shows practical ways to keep improving models anyway.
- Don’t just make one model huge. Train multiple smaller models and combine them. It’s a better use of limited data.
- Use stronger regularization than usual when data is tight. It prevents overfitting and unlocks steady progress.
- Distillation lets you enjoy the benefits of “many models” while deploying just one—so it’s efficient at use time.
- These ideas transfer beyond pre-training from scratch: they also help continued pre-training on new domains like math.
Takeaway
If you can’t get much more data but have a lot of compute, the best recipe is:
- Train with strong regularization to avoid overfitting,
- Prefer many smaller models combined (ensembles) over one giant model,
- Then distill the ensemble into a single compact model for easy use.
This approach gets much more out of the same data—today and likely in the data-limited future.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper, articulated so future researchers can act on them.
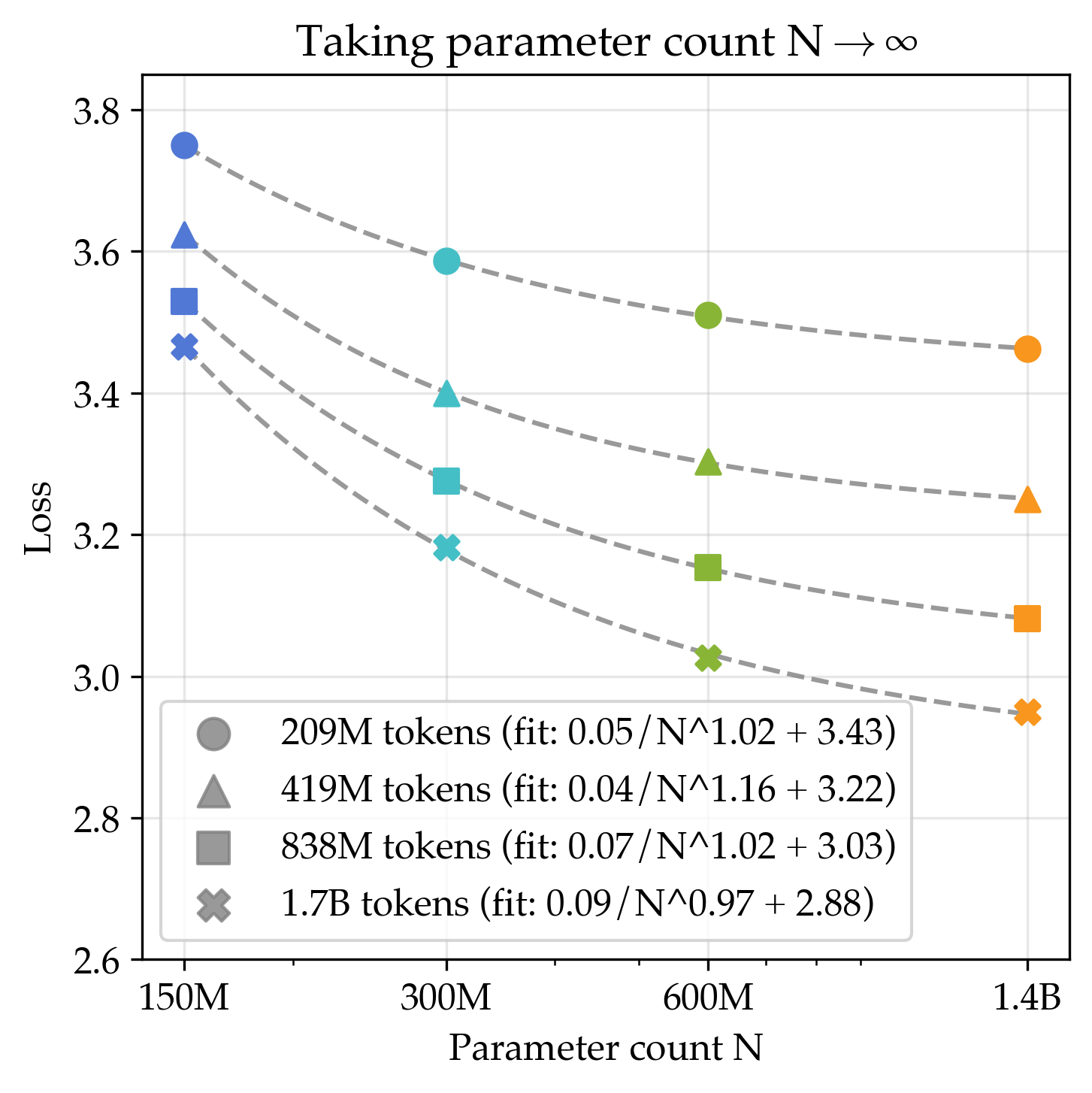
- External validity across data scales: Findings are demonstrated on seed token counts up to 1.6B; it is unclear whether regularized scaling, ensemble asymptotes, and data-efficiency gains hold at tens to hundreds of billions of tokens or on truly web-scale corpora. Replicate at much larger D (e.g., 10–100B) and across diverse domains (code, math, multilingual) to test robustness.
- Dataset representativeness and contamination: The paper uses DCLM web text but does not quantify overlap/contamination with downstream benchmarks or privacy/memorization risks under heavy epoching. Conduct deduplication, contamination audits, and membership-inference tests to separate genuine generalization from memorization.
- Architecture dependence: Results are specific to Llama-style transformers with AdamW. It is unknown whether the same asymptotic advantages and regularization needs apply to other architectures (e.g., MoE, Mamba/State Space Models, RWKV, GPT-J style), different tokenizer regimes, or longer context lengths. Systematically evaluate across architecture families and context windows.
- Regularization scope and mechanisms: Only weight decay is tuned. Effects of other regularizers (dropout, label smoothing, stochastic depth, spectral/orthogonal regularization, gradient noise, data augmentation, mixout, Bayesian priors) on overfitting and scaling laws remain unexplored. Compare and combine regularizers to establish a principled recipe under data scarcity.
- Optimizer and schedule sensitivity: The paper uses AdamW with cosine LR. The impact of optimizers (Adafactor, Lion, Shampoo, SGD+momentum) and schedules (linear, step, one-cycle), including coupling with strong weight decay, is not tested. Perform optimizer-level ablations tied to scaling performance and asymptotes.
- Reliability of power-law extrapolation: Asymptotes are fitted from few points (4 N values, 5 K values) and limited seeds. This may be fragile. Increase the number of scales and seeds, report confidence intervals, test alternative functional forms (e.g., log-linear, double power laws, saturating models), and perform model selection to validate asymptote estimates.
- Order-of-limits and monotonicity assumptions: The joint limit assumes monotone decrease in loss with N and K when the other is fixed and that order of limits does not matter. Provide empirical tests and theoretical conditions under which limN→∞ limK→∞ equals limK→∞ limN→∞, or characterize when they diverge.
- Ensemble diversity and construction: Ensembles rely on initialization and data order randomness; the degree of “multi-view” diversity is not quantified. Measure and increase diversity via data partitioning/bagging, augmentation, different tokenizers, architectures, or training seeds; paper how diversity correlates with asymptote reductions.
- Alternative ensemble methods: Only logit averaging of independent models is explored. Compare to snapshot ensembles, SWA, dropout-as-ensemble, stacking/metalearning, Bayesian model averaging, mixture-of-experts (MoE) with static/dynamic routing, and hierarchical/heterogeneous ensembles to assess asymptote improvements and efficiency trade-offs.
- Hyperparameter tuning for ensembles: The heuristic “2× epochs, 0.5× weight decay” for large-K ensembles is ad hoc. Formulate and solve a bilevel optimization for ensemble member hyperparameters targeting the K→∞ asymptote; quantify sensitivity and derive principled tuning rules.
- Inference compute and deployment constraints: Ensembles linearly increase test-time compute and latency. The paper partially addresses this via distillation, but a comprehensive cost–quality frontier (latency, memory, throughput) and serving strategies (e.g., partial ensemble at generation, early-exit, speculative decoding with ensembles) are not analyzed.
- Distillation design space: Distillation uses sequence-level KD with unconditional sampling and a mixture of real+synthetic data; details like sampling temperature, D’/D ratio, prompting, and teacher signal type (soft targets vs hard samples) are not fully explored. Systematically vary these and compare with standard KD (KL to teacher logits), policy distillation, and conditional generation strategies.
- Self-distillation stability and collapse boundaries: Self-distillation improves loss at 300M, but the conditions preventing model collapse are not characterized (e.g., synthetic/real mixing ratios, sampling temperatures, iterative rounds). Map the safe operating region and failure modes across sizes and datasets.
- Generalization beyond small downstream suites: Validation loss correlates with three small benchmarks (PIQA, SciQ, ARC Easy) and math CPT. A broader suite (reasoning-heavy tasks, coding, multilingual, safety/toxicity, calibration, long-context recall) is needed to establish whether asymptote/loss gains translate to real-world capability gains.
- Safety, toxicity, and alignment implications: Heavy epoching, ensemble-induced overfitting, and synthetic data may change safety profiles. Evaluate toxicity, bias, factuality, and calibration shifts induced by ensembling and distillation; assess alignment impacts in instruction-tuned or RLHF settings.
- Data repetition strategies: The paper finds overfitting with naive epoching but does not assess sophisticated repetition curricula (e.g., progressive mixing, temperature-based sampling, difficulty-aware schedules, dedup-aware reweighting). Design repetition policies that mitigate overfitting while improving sample efficiency.
- Layer-wise and parameter-group regularization: Uniform weight decay is used; layer-wise/adaptive WD (e.g., decoupled WD per layer, norm-based WD, AdamW’s decoupled WD nuances), embedding WD, and attention/MLP-specific regularization could change scaling behavior. Explore finer-grained schemes.
- Theoretical underpinning for deep LMs: The argument for optimal regularization monotonicity draws from overparameterized regression. Extend theory to deep autoregressive LMs under data scarcity, specifying assumptions that guarantee monotone scaling and lower ensemble asymptotes.
- Multi-view structure in language data: The ensemble advantage is hypothesized to arise from “multi-view” features. Empirically test for multi-view structure in LLMing (e.g., via feature attribution, representation probing, diversity metrics) and relate it to ensemble gains.
- Entropy-asymptote hypothesis: The paper suggests asymptotes may converge to text entropy under infinite data/compute. Estimate entropy by domain, quantify the gap to Bayes-optimal error, and test whether different recipes share the same E and α at larger scales.
- CPT generalization: The CPT improvements are shown for math with Llama 3.2 3B. Validate on varied base models and mid-train datasets (general reasoning, instruction-following, code), and characterize whether ensemble/CPT recipes interact beneficially or adversely with subsequent SFT/RLHF.
- Reproducibility and reporting details: While runs/code are open-sourced, key details that affect overfitting and scaling (exact data preprocessing, deduplication, validation split construction, tokenizer settings, seed handling) need exhaustive documentation to enable precise replication and contamination control.
- Environmental and cost trade-offs: Infinite compute framing abstracts away energy and cost constraints. Quantify wall-clock, FLOPs, and energy for N-scaling vs K-scaling, and provide cost-aware guidance on when ensembles plus distillation outperform single large models in practice.
Glossary
- AdamW optimizer: A variant of Adam that decouples weight decay from gradient-based updates to improve regularization. "AdamW optimizer with cosine learning rate schedule"
- Asymptote: The limiting value a scaling curve approaches as the resource (e.g., parameters or ensemble size) goes to infinity. "By preferring recipes with lower loss asymptotes, we can train better models at sufficiently high compute budgets."
- Asymptotic statistics: The paper of statistical properties in the limit of large sample sizes, used here to reason about behavior under infinite data/compute. "Asymptotic statistics suggests that the asymptotes are equal if the algorithms achieve Bayes-optimal error under infinite data and compute, in which case their loss would be the entropy of text"
- Auto-regressive recipe: A training setup where models predict the next token given previous ones. "we follow a standard auto-regressive recipe, using Llama-style architecture, AdamW optimizer with cosine learning rate schedule, context length 4096, etc."
- Bayes-optimal error: The lowest possible error achievable with perfect knowledge of the data distribution. "the asymptotes are equal if the algorithms achieve Bayes-optimal error under infinite data and compute"
- Chinchilla (scaling law): A compute-optimal scaling rule recommending data and parameter co-scaling with a specific ratio. "Under train compute constraints, scaling recipes like Chinchilla recommend jointly increasing data and model size with 20× more tokens than parameters"
- Continued pre-training (CPT): Further training of a pre-trained model on additional data to adapt or improve capabilities. "We also test the immediate applicability of our interventions for continued pre-training (CPT) on the MegaMath-Web-Pro dataset"
- Coordinate descent: An optimization method that iteratively tunes one hyperparameter at a time while keeping others fixed. "we use a coordinate descent algorithm inspired by"
- Cosine learning rate schedule: A schedule where the learning rate follows a cosine curve over training to smoothly anneal. "AdamW optimizer with cosine learning rate schedule"
- Data efficiency: How effectively an algorithm converts data into performance, often measured as how much less data is needed to reach a target loss. "resulting in a 17.5× data efficiency improvement."
- Data processing inequality: A principle stating that post-processing cannot increase information relevant to a target, used to question self-distillation gains. "following arguments such as the data processing inequality."
- Double descent: A phenomenon where test error first decreases, then increases, and eventually decreases again as model capacity grows. "even when loss does not monotonically decrease due to double descent"
- Ensemble distillation: Compressing the performance of an ensemble into a single model via distillation. "Ensemble distillation and self-distillation."
- Ensemble member count: The number of individual models combined in an ensemble. "the ensembling recipe achieves a lower loss asymptote as ensemble member count approaches infinity"
- Ensemble scaling: Improving performance by increasing the number of ensemble members rather than model size. "Composing parameter scaling and ensemble scaling further improves the asymptote"
- Ensembling: Combining multiple independently trained models to improve robustness and accuracy, often by averaging outputs. "we average the logits of K independently trained models"
- Entropy of text: The theoretical limit on compressibility or predictability of text; a lower bound on achievable loss. "their loss would be the entropy of text"
- FLOPs: Floating point operations, a measure of computational cost for training/inference. "The number of FLOPs needed to generate from or evaluate an ensemble is simply the sum of the costs for all members."
- Held-out i.i.d. validation set: A separate dataset sampled independently and identically from the same distribution for unbiased evaluation. "we defer to loss on a held-out i.i.d. validation set"
- Joint scaling recipe: A method that simultaneously scales both model size and ensemble size to achieve lower asymptotic loss. "Composing parameter scaling and ensemble scaling further improves the asymptote"
- Logit averaging: Combining model outputs by averaging their pre-softmax scores (logits). "we average the logits of K independently trained models"
- Logits: Pre-softmax scores output by a model, representing unnormalized log probabilities. "we average the logits of K independently trained models"
- Llama-style architecture: A specific transformer-based architecture used for LLM training. "using Llama-style architecture"
- Monotone scaling: A property where loss consistently decreases as a resource (e.g., parameters) increases. "loss follows monotone scaling in parameter count"
- Multi-view structure: A data property where multiple distinct features can individually explain outcomes, motivating ensembles. "Under this 'multi-view' structure"
- Over-parameterized regression: Regression models with more parameters than data points, often requiring strong regularization. "theory for over-parameterized regression"
- Overfitting: When a model memorizes training data patterns and performs worse on validation/test data. "the models start overfitting and loss starts increasing"
- Parameter scaling: Increasing the number of model parameters to improve performance under certain regimes. "Comparing scaling parameter count vs scaling ensemble member count."
- Parameter-to-token ratio: The ratio of model parameters to training tokens, impacting overfitting and scaling behavior. "parameter-to-token ratios 140× larger than Chinchilla"
- Power law: A functional form where performance scales as a power of resources, often with an asymptote. "loss closely follows a power law in N"
- Regularization: Techniques (e.g., weight decay) that constrain model learning to reduce overfitting. "it is critical to regularize pre-training with much higher weight decay than standard practice."
- Self-distillation: Training a student model using outputs from a teacher of the same architecture/size. "We also find that self-distilling a 300M teacher into a student of the same architecture surprisingly reduces loss"
- Sensitivity analysis: An assessment of how variations (e.g., random seeds) affect estimated metrics like asymptotes. "we share a sensitivity analysis"
- Sequence-level knowledge distillation: Distillation that trains a student on sequences generated by a teacher rather than token-level soft targets. "via sequence-level knowledge distillation"
- Weight decay: An L2 penalty on parameters during optimization, used to control overfitting. "defaulting to a weight decay of 0.1"
Collections
Sign up for free to add this paper to one or more collections.