Nonlinear Independent Component Analysis Scheme and its application to gravitational wave data analysis (2509.09632v1)

Abstract: Noise subtraction is a crucial process in gravitational wave (GW) data analysis to improve the sensitivity of interferometric detectors. While linear noise coupling has been extensively studied and successfully mitigated using methods such as Wiener filtering, subtraction of non-linearly coupled and non-stationary noise remains a significant challenge. In this work, we propose a novel independent component analysis (ICA)-based framework designed to address non-linear coupling in noise subtraction. Building upon previous developments, we derive a method to estimate general quadratic noise coupling while maintaining computational transparency compared to machine learning approaches. The proposed method is tested with simulated data and real GW strain data from KAGRA. Our results demonstrate the potential of this framework to effectively mitigate complex noise structures, providing a promising avenue for improving the sensitivity of GW detectors.

• The paper introduces a nonlinear ICA technique to isolate statistically independent components from nonlinear noise processes in gravitational wave data.
• It employs KL divergence minimization and convolutional kernel estimation to subtract bi-linear noise coupling, improving signal-to-noise ratios.
• The method demonstrates enhanced noise subtraction in both simulated and KAGRA data, promising advancements in real-time gravitational wave detection.

Nonlinear Independent Component Analysis Scheme for Gravitational Wave Data

The paper "Nonlinear Independent Component Analysis Scheme and its application to gravitational wave data analysis" (2509.09632) explores a novel ICA technique designed to address the non-linear noise coupling present in gravitational wave (GW) data. This work is situated in the context of enhancing the sensitivity of GW interferometers like LIGO and KAGRA, where complex noise structures often obscure weak signals from astrophysical events.

ICA Extension to Nonlinear Mixing

Linear Model Overview

Traditional ICA approaches focus on linear mixing, where observed signals are decomposed into independent components. This paper starts with the linear model, where observables are a linear combination of source signals, aiming to find a transformation matrix to achieve statistical independence. The Kullback-Leibler (KL) divergence is utilized to measure independence, offering a way to optimize the transformation matrix using distributional properties of the signals.

Nonlinear Extension

The need to handle nonlinearities leads to an extension of ICA for systems where observables relate nonlinearly to source signals. By minimizing the KL divergence, the paper proposes a framework that identifies statistically independent components even in the presence of quadratic noise coupling. This is crucial for advancing GW data analysis, where noise often exhibits non-linear and non-stationary characteristics.

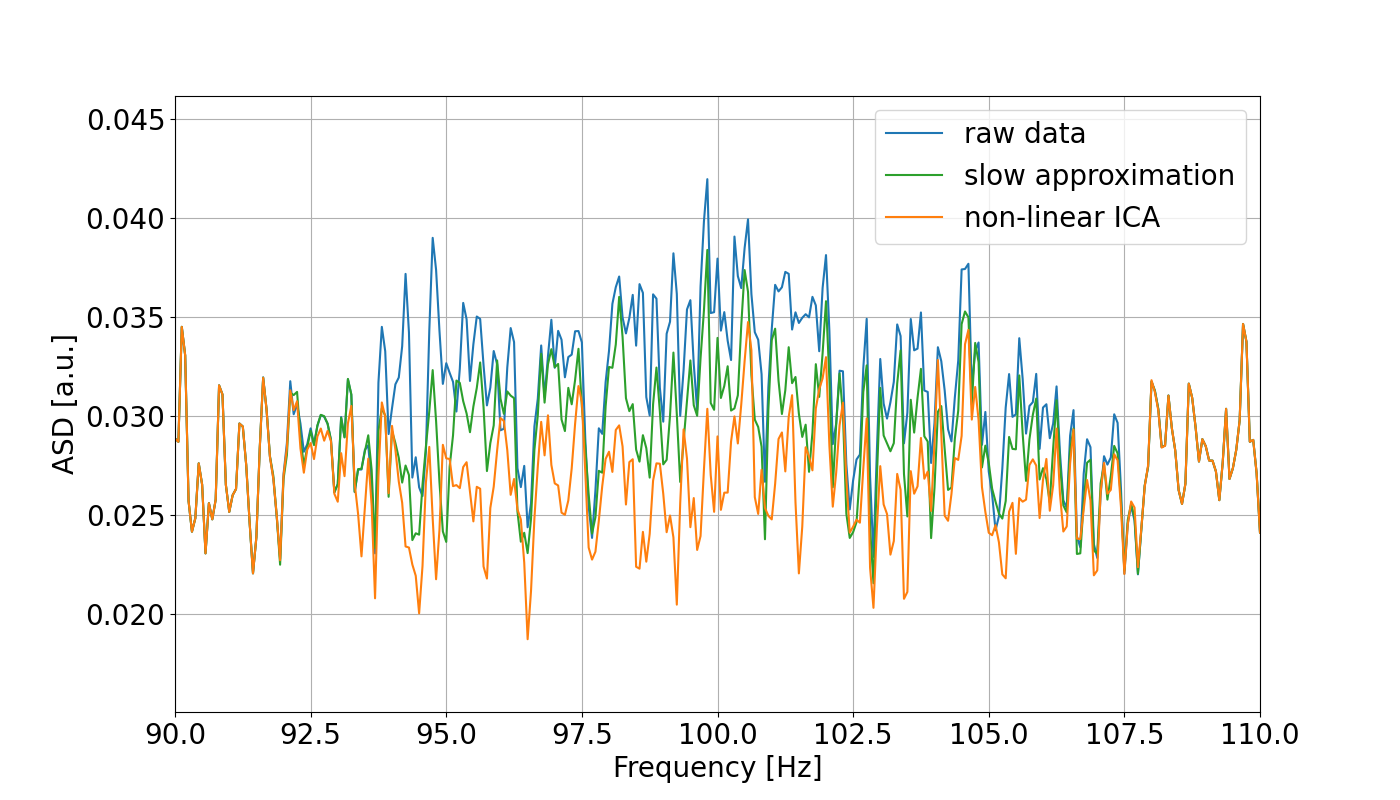
Figure 1: ASD of the data which only includes the noise components. The three curves correspond to: raw data (blue), the result after applying the slow approximation method (green), and the result after applying the non-linear ICA (orange).

Bi-Linear Coupling and Subtraction

Model and Estimation Method

The paper models bi-linear coupling, a common non-linear interaction in experimental data, particularly GW strain data. A convolutional kernel describes the coupling between different noise sources. The subtraction method adapts ICA to estimate this kernel, thereby facilitating noise reduction through spectral manipulation.

Practical Implementation

The implementation utilizes Welch's method for kernel estimation, ensuring computational efficiency. The subtraction approach is evaluated using simulated data, with test signals injected to assess the improvement in signal-to-noise ratio (SNR). The method demonstrates improved noise subtraction over existing techniques, especially in cases without hierarchical frequency assumptions.

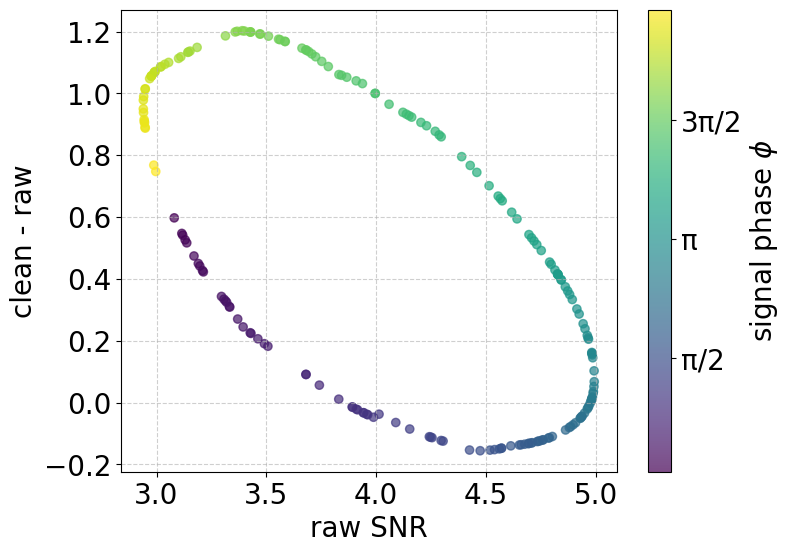
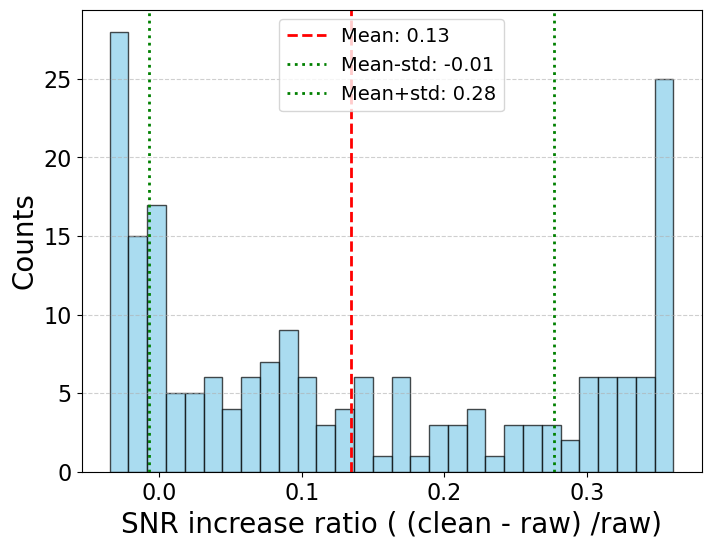
Figure 2: Change in SNR before (horizontal axis) and after (vertical axis) ICA, for 100 realizations of the injected signal with randomly chosen phase $\phi \in [0,2\pi]$. Each point is color-coded by the corresponding signal phase.

Real-World Application and Results

Application to KAGRA Data

Applying the method to real KAGRA data, the authors injected controlled noise into the system and identified nonlinear couplings contributing to spectral sidebands. The ICA-based subtraction effectively reduced these noise components, outperforming traditional linear subtraction methods.

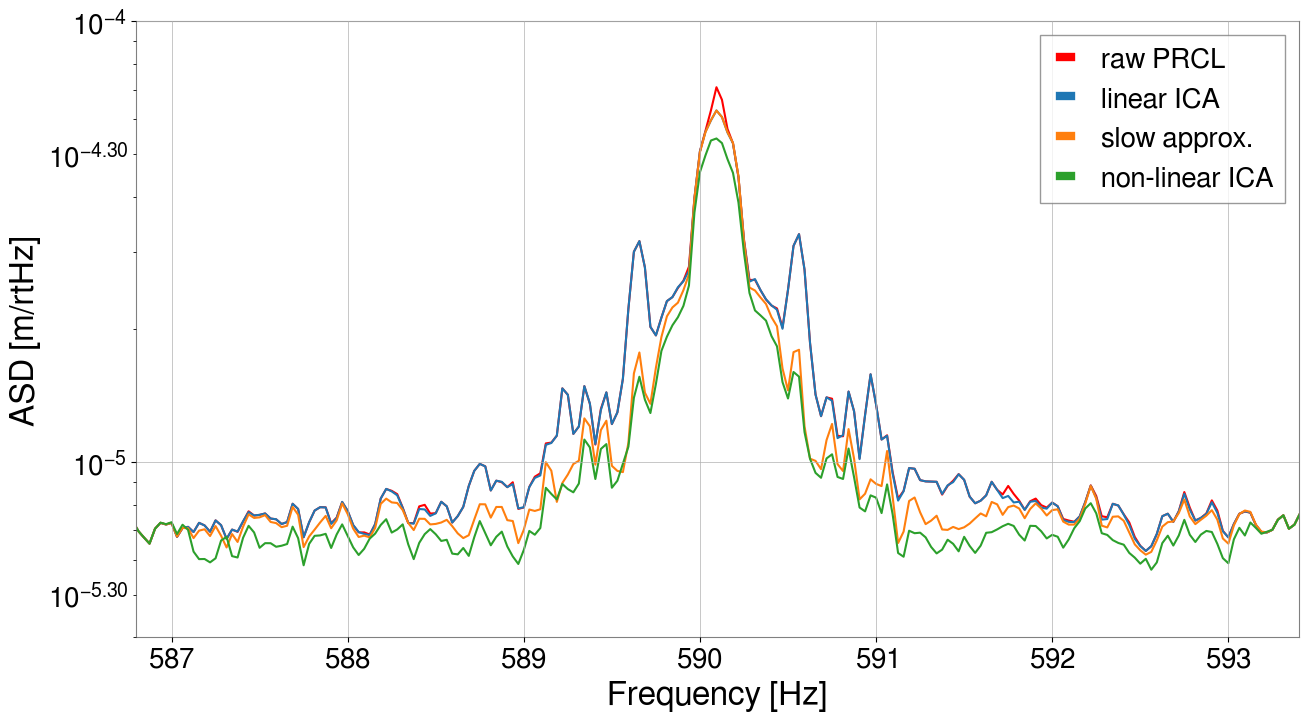
Figure 3: ASD of the PRCL around the spectral peak at 590 Hz, shown before subtraction (red) and after applying different cleaning methods: linear ICA (blue), slow-approximation method (orange), and non-linear ICA (green).

Discussion and Prospects

Strengths and Limitations

The proposed nonlinear ICA scheme offers a robust framework for mitigating complex noise in GW detectors. Its ability to handle general quadratic coupling broadens the applicability beyond previous methods that rely on simplifications. However, the implementation requires precise knowledge of noise characteristics and sufficient computational resources for real-time deployment.

Future Directions

Future research should explore the integration of multiple channels and complex non-linear couplings, possibly leveraging advanced machine learning techniques for further performance gains. Ensuring the method's adaptability to different noise scenarios will be key to scaling it within real-time data analysis pipelines in large-scale observatories.

Conclusion

This paper presents a significant advancement in ICA by extending its capabilities to handle nonlinear noise coupling in GW data. The method's demonstrated effectiveness in both simulated and real-world scenarios marks a promising step towards enhancing the sensitivity and accuracy of gravitational wave detection.