Photonic Matrix Multiplication Circuit Based on Double Racetrack Resonator Building Blocks (2509.09445v1)

Abstract: This paper presents a novel design framework for photonic matrix multiplication based on programmable photonic integrated circuits using double racetrack (DRT) resonators as building blocks. Here, we analytically demonstrate that the transfer function of the DRT resonator building block resembles that conventional building blocks, such as directional couplers and MZI, making it suitable for building programmable circuits that handle complex matrix calculations. Using this new DRT resonators building block, a 3-by-3 photonic processor is implemented and validated through full-wave Finite Element Method (FEM) simulations, and scalability is further analysed using hybrid FEM-circuit modelling. Additionally, we implement a low-pass filter as a non-unitary system example, showcasing the flexibility of the approach. Results confirm high fidelity between simulated and analytical models, supporting the viability of DRT resonators for reconfigurable photonic circuits. We believe that the proposed DRT resonator building blocks have the potential to complement and integrate with other previously reported blocks, thereby enhancing the fidelity and expanding the application scope of programmable photonic integrated circuits, particularly for all-optical signal processing in communication systems and for integration within microwave photonics platforms targeting emerging telecommunications technologies.

• The paper introduces a scalable photonic matrix multiplication design using DRT resonators, offering improved tunability and reconfigurability.
• It employs advanced techniques like Singular Value Decomposition and genetic algorithms to precisely decompose matrices and configure phase shifts.
• FEM simulations validate the design, demonstrating high-fidelity transmission with minimal Normalized Square Error across circuits.

Photonic Matrix Multiplication Circuit Based on Double Racetrack Resonator Building Blocks

Introduction

This paper introduces a design framework for photonic matrix multiplication circuits using Double Racetrack (DRT) resonator building blocks. This novel approach provides a scalable and flexible method for designing programmable Photonic Integrated Circuits (PICs) tailored for complex matrix calculations. DRT resonators are proposed as a replacement for traditional building blocks such as Directional Couplers (DC) and Mach-Zehnder Interferometers (MZIs). These offer improved tunability, spectral control, and integration, making them optimal for compact and reconfigurable optical signal processing circuits.

Double Racetrack Resonator Building Block

The DRT resonator functions as the fundamental component within the proposed circuit design, offering a compact and efficient way to manipulate optical signals. The core principle involves configuring the physical layout and equivalent circuit model of the DRT, which mirrors the functionalities of conventional DCs and MZIs. This is achieved through precise control over coupling coefficients and phase shifts using refractive index tuning, facilitating the development of reconfigurable circuits.

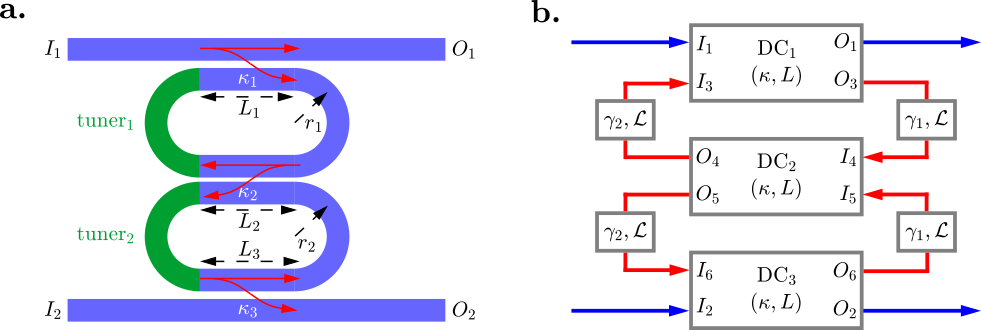
Figure 1: (a) Physical layout of DRT resonator building block. (b) Equivalent circuit model.

Circuit Design Framework

DRT resonator-based circuits are synthesized using a unique framework that relies on decomposing target unitary matrices. This process is conducted through mathematical techniques, such as Singular Value Decomposition (SVD) and Genetic Algorithms (GA), enabling the construction of photonic circuits that perform specific linear operations.

Key to this framework is the synthesis of the DRT circuit, consisting of programmable units that manipulate input signals through tailored phase shifts $\phi$ and amplitudes $\theta$ derived from the matrix decomposition. The practicality of this model is validated by implementing 3-by-3 matrix multiplication circuits and unitary operations, which are efficiently configured using finite element method (FEM) simulations.

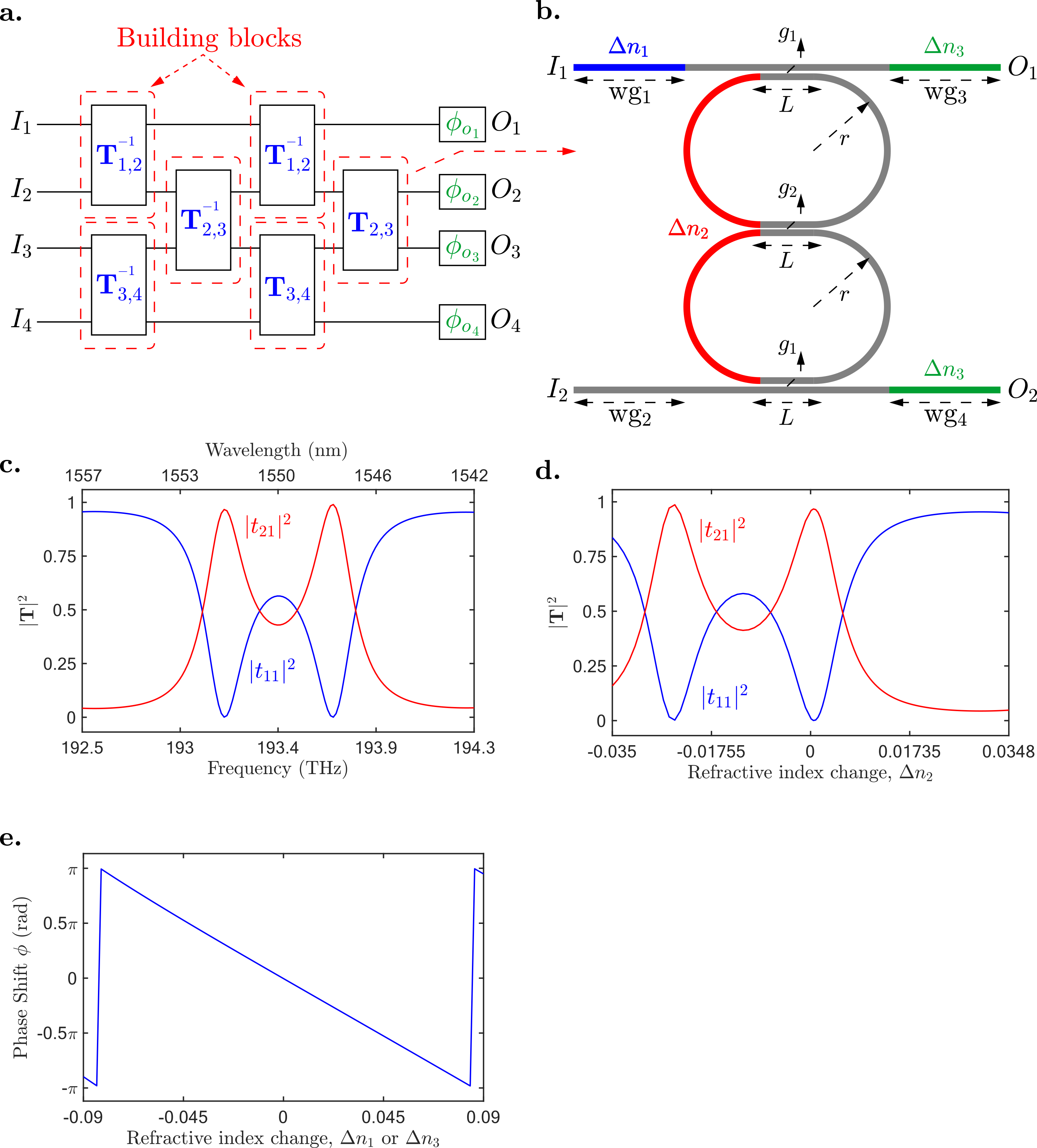
Figure 2: (a) An example of 4-by-4 PIC with required building blocks and output phase shifts $\phi_o$. (b) DRT geometry layout and its design parameters. (c) Spectrum of the magnitude of the bar transmission $|t_{11}|^2$.

Results and Validation

Using FEM simulations, the effectiveness of the DRT-based PIC framework is demonstrated through accurate representation and implementation of target matrices. The paper shows the ability to achieve high fidelity in transmission parameters, revealing minimal Normalized Square Error (NSE) between simulated and ideal matrices.

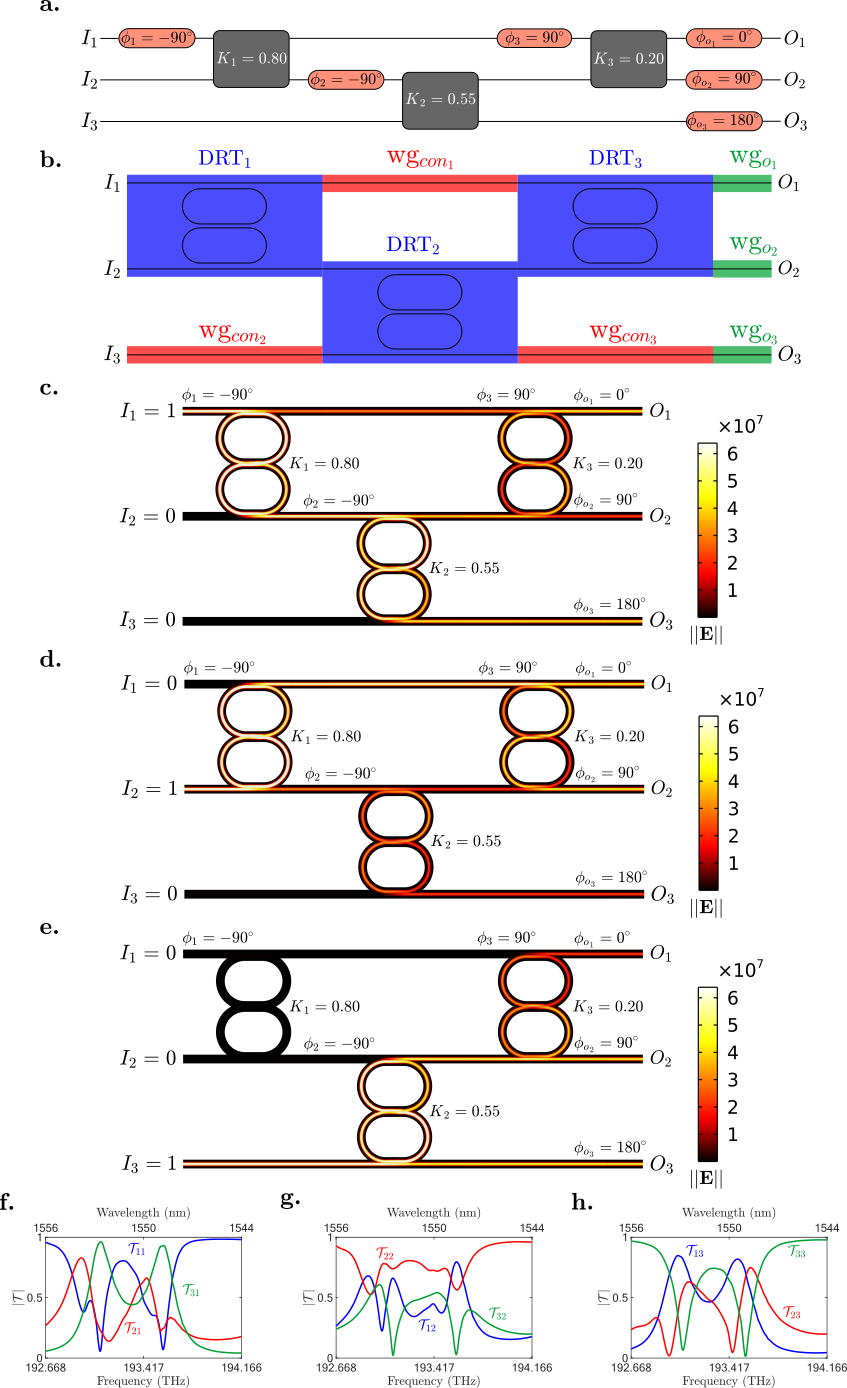
Figure 3: (a) Schematic of the practical realization of the 3-by-3 unitary matrix.

The scalability analysis shows a linear increase in NSE proportional to the matrix size, indicating room for further optimization in larger DRT-based circuits. Comparatively, DRT-based systems provide a narrower operational bandwidth than DC counterparts, highlighting potential trade-offs between precision and bandwidth in spectral applications.

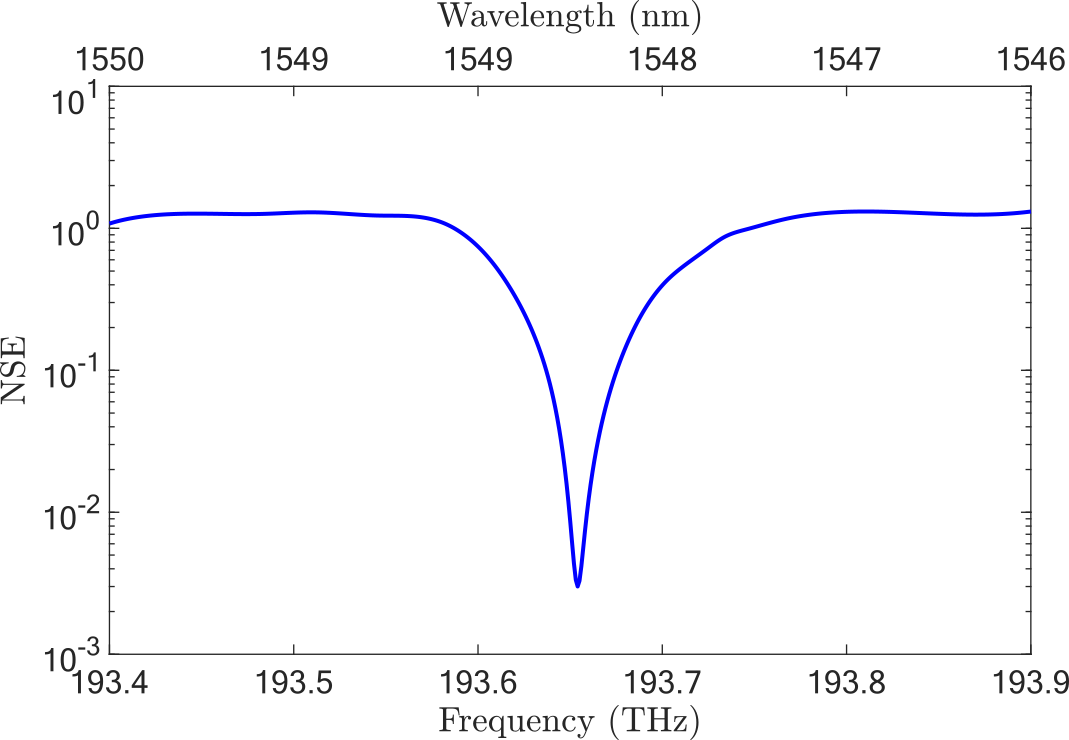
Figure 4: Normalized Square Error (NSE) as a function of frequency for the example 3-by-3 photonic integrated circuit.

Analogue Optical Signal Filter Implementation

The practical applicability of DRT-based PICs is further explored through the implementation of an analog optical IIR filter. By leveraging the framework to convert a non-unitary system into a unitary matrix via GAs, the paper confirms the capability of integrating complex signal processing functions within a photonic platform. This confirms the utility of DRT structures for diverse applications in optical telecommunications and signal processing spheres.

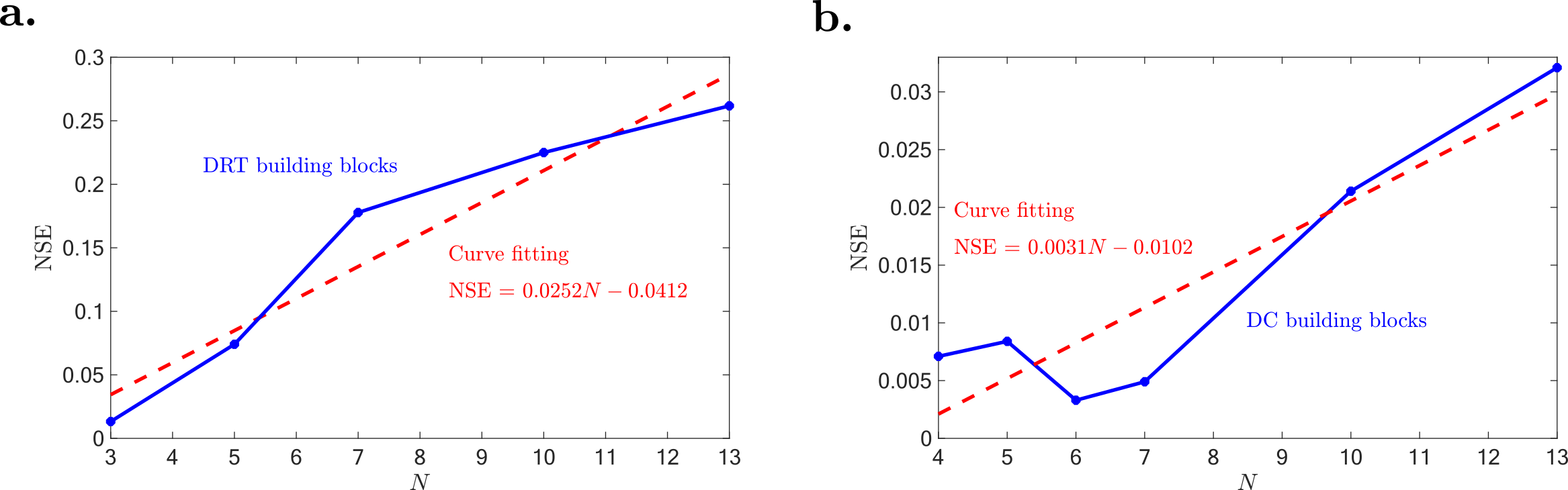
Figure 5: (a) NSE vs different sizes of PIC using DRT building blocks. (b) NSE vs different sizes of PIC using DC building blocks.

Conclusion

The framework for DRT resonator-based photonic integrated circuits presents a promising approach for achieving scalable, high-fidelity optical processing. Despite existing challenges in scalability, the results indicate its significant potential in enhancing the functionality of PICs, particularly in narrow-band and reconfigurable optical systems. Future developments are likely to focus on further minimizing NSE and broadening the bandwidth capabilities, opening doors to new applications in advanced photonic technologies.