The Majority is not always right: RL training for solution aggregation (2509.06870v1)

Abstract: Scaling up test-time compute, by generating multiple independent solutions and selecting or aggregating among them, has become a central paradigm for improving LLMs on challenging reasoning tasks. While most prior work relies on simple majority voting or reward model ranking to aggregate solutions, these approaches may only yield limited benefits. In this work, we propose to learn aggregation as an explicit reasoning skill: given a set of candidate solutions, we train an aggregator model to review, reconcile, and synthesize a final, correct answer using reinforcement learning from verifiable rewards. A key ingredient is careful balancing of easy and hard training examples, allowing the model to learn both to recover minority-but-correct answers as well as easy majority-correct answers. Empirically, we find our method, AggLM, outperforms both strong rule-based and reward-model baselines, across multiple benchmarks. Furthermore, it generalizes effectively to solutions from differing models, including stronger ones than contained in the training data, all while requiring substantially fewer tokens than majority voting with larger numbers of solutions.

• The paper demonstrates that RL-trained aggregation with AggLM effectively synthesizes partial solutions to overcome the limitations of majority voting.
• The methodology employs verifiable binary rewards on math benchmarks, achieving accuracy boosts up to 79.7% compared to standard approaches.
• The approach is token-efficient and robust, generalizing across candidate set sizes and recovering correct answers in challenging, minority scenarios.

Reinforcement Learning for Solution Aggregation: The AggLM Approach

Introduction

The paper "The Majority is not always right: RL training for solution aggregation" (2509.06870) addresses a central challenge in leveraging LLMs for complex reasoning tasks: how to aggregate multiple independently generated solutions to maximize accuracy. While majority voting and reward-model-based selection are standard, these methods are limited by their inability to recover correct minority solutions and to synthesize partial correctness across candidates. The authors propose AggLM, a reinforcement learning (RL)-trained aggregator model that explicitly learns to review, reconcile, and synthesize final answers from sets of candidate solutions. This essay provides a technical summary of the methodology, experimental findings, and implications for future research.

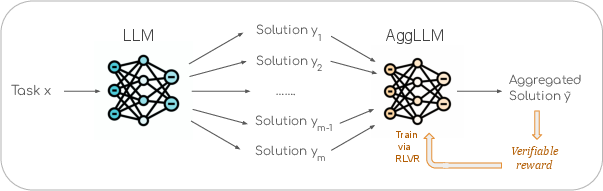
Figure 1: AggLM: given a task and sampled LLM solutions as input, AggLM uses reasoning to review, reconcile, and synthesize a final aggregated solution which is typically superior to the original solutions.

Methodology

Problem Formulation

Given a problem $x$ and a set of $m$ candidate solutions $y_{1:m}$ sampled from a solution model $p_\theta(y|x)$, the goal is to train an aggregation model $p_\phi(\tilde{y}|x, y_{1:m})$ that outputs an aggregated solution $\tilde{y}$. The aggregation model is trained using reinforcement learning from verifiable rewards (RLVR), where the reward is binary: $r(\tilde{y}) = \mathbbm{1}[\tilde{y} = y^\star]$, with $y^\star$ being the ground-truth solution.

Training Data Construction

To ensure the aggregator learns both to select correct majority answers and to recover minority-but-correct answers, the training set is constructed by sampling $s \cdot m$ solutions per problem and grouping them into $s$ sets of $m$ solutions. Sets are labeled as "easy" if the majority answer is correct and "hard" otherwise. The final training mixture includes all hard examples and a tunable proportion $p\%$ of easy examples, balancing the need for challenging cases with sufficient coverage of typical scenarios.

RL Optimization

The aggregation policy is optimized using Group-Relative Policy Optimization (GRPO), with group size $m=8$, KL regularization, and a sampling temperature of 1.5. The aggregator is initialized from Qwen3-1.7B and trained on the DeepScaler dataset, comprising 40k math problems with ground-truth solutions. The prompt template instructs the model to review, correct, and synthesize a final solution from the provided candidates.

Experimental Results

Aggregation Performance

AggLM-1.7B is evaluated on four MathArena benchmarks (AIME24, AIME25, HMMT24, HMMT25), aggregating solutions from Qwen3-1.7B and Qwen3-8B in both "thinking" and "non-thinking" modes. The RL-trained aggregator consistently outperforms majority voting, reward-model-based selection (AceMath-7B/72B), and prompted aggregation without RL.

Key numerical results:

• On AIME25, aggregating Qwen3-1.7B solutions, AggLM-1.7B achieves 50.0% accuracy, compared to 45.9% for majority voting and 40.3% for AceMath-7B best-of-N.
• When aggregating Qwen3-8B solutions, AggLM-1.7B achieves 79.7% on AIME25, outperforming majority voting (78.7%) and all reward-model baselines.
• On non-thinking solutions, AggLM-1.7B maintains top performance, demonstrating robustness to weaker or noisier candidate sets.

  Figure 2: Performance vs. number of candidate solutions $k$ for different aggregation methods. AggLM-1.7B is superior to other methods at $k=8$ (its training regime), and generalizes well to both larger and smaller $k$.

Scaling and Generalization

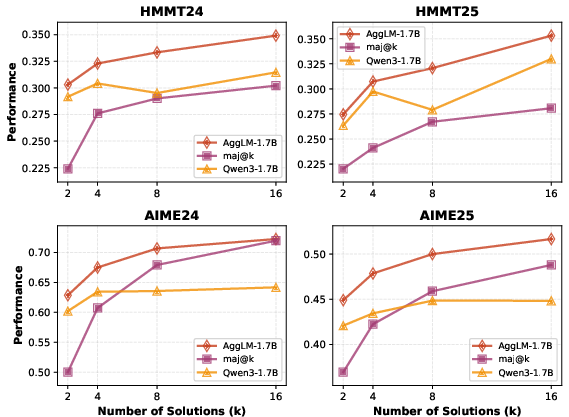
AggLM-1.7B, trained at $k=8$, generalizes to both smaller and larger $k$, with performance improving as $k$ increases. Its scaling curve is steeper than majority voting, indicating better utilization of additional candidates. Notably, AggLM-1.7B with $k=8$ outperforms majority voting with $k=16$ on several datasets, demonstrating superior token efficiency.

Minority Recovery and Hard Cases

AggLM's gains over majority voting are most pronounced when the majority answer set is small—i.e., when candidate solutions are diverse and the correct answer is a minority. In these hard cases, AggLM's reasoning and synthesis capabilities enable it to recover correct answers that majority voting misses.

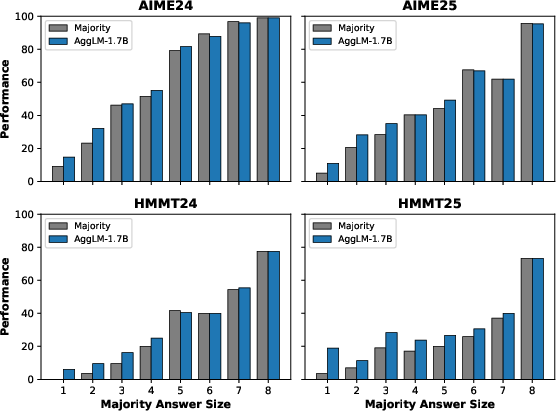
Figure 3: Performance vs. majority answer size for AggLM compared to majority vote. AggLM outperforms majority vote in harder cases (small majority size) and matches it in easier cases.

Ablation Studies

• Training Mixture: Including a moderate proportion (5–50%) of easy examples in the training mixture yields optimal performance. Hard-only or all-easy mixtures are suboptimal.
• Number of Solution Sets: Increasing the number of solution sets per problem ($s$) provides only marginal gains, suggesting diminishing returns from additional diversity.
• Aggregator vs. Solution Model Training: Fine-tuning the solution model on the aggregator's data yields minimal improvement, confirming that aggregation, not extra data, is responsible for the observed gains.
• Token Efficiency: Aggregator models use roughly one-third the tokens of solution models, making AggLM more cost-effective for a given accuracy target.
• Unified Model: Multitask training of a single LLM for both solution generation and aggregation achieves performance close to dedicated models, suggesting that aggregation can be integrated into unified LLM architectures.

Practical and Theoretical Implications

The AggLM approach demonstrates that aggregation can be learned as a reasoning skill, not merely a heuristic. RLVR enables the model to synthesize new, correct solutions by combining partial correctness across candidates, a capability unattainable by majority voting or reward-model selection. The method is robust to out-of-distribution candidate sets, generalizes across model strengths and solution modes, and is token-efficient.

Practically, AggLM can be deployed as a post-processing module for any LLM, requiring only verifiable reward signals for training. The approach is particularly valuable in domains where correct answers are rare or diverse, such as mathematics, code generation, and scientific reasoning. Theoretically, the results challenge the sufficiency of majority-based aggregation and highlight the importance of explicit reasoning in solution synthesis.

Future Directions

Potential extensions include:

• Integrating aggregation and solution generation in a single LLM, leveraging multitask training.
• Applying RL-trained aggregation to other domains (e.g., code, scientific QA) and modalities.
• Using the aggregator to distill improved reasoning skills back into the base solution model.
• Exploring more sophisticated reward functions, including partial credit and uncertainty calibration.

Conclusion

The AggLM framework establishes that explicit, RL-trained aggregation outperforms majority voting and reward-model selection for LLM-based reasoning tasks, especially in hard cases where correct answers are in the minority. The approach is robust, generalizes across models and candidate set sizes, and is token-efficient. These findings motivate further research into learned aggregation as a core component of LLM reasoning pipelines and suggest that future LLMs should natively support aggregation as a first-class capability.