GeoSplat: A Deep Dive into Geometry-Constrained Gaussian Splatting (2509.05075v1)

Abstract: A few recent works explored incorporating geometric priors to regularize the optimization of Gaussian splatting, further improving its performance. However, those early studies mainly focused on the use of low-order geometric priors (e.g., normal vector), and they are also unreliably estimated by noise-sensitive methods, like local principal component analysis. To address their limitations, we first present GeoSplat, a general geometry-constrained optimization framework that exploits both first-order and second-order geometric quantities to improve the entire training pipeline of Gaussian splatting, including Gaussian initialization, gradient update, and densification. As an example, we initialize the scales of 3D Gaussian primitives in terms of principal curvatures, leading to a better coverage of the object surface than random initialization. Secondly, based on certain geometric structures (e.g., local manifold), we introduce efficient and noise-robust estimation methods that provide dynamic geometric priors for our framework. We conduct extensive experiments on multiple datasets for novel view synthesis, showing that our framework: GeoSplat, significantly improves the performance of Gaussian splatting and outperforms previous baselines.

• The paper introduces a curvature-guided optimization framework for 3D Gaussian splatting, achieving enhanced scene rendering fidelity and reduced artifacts.
• It employs robust manifold and varifold-based geometric estimation methods that dynamically integrate first- and second-order priors into the splatting pipeline.
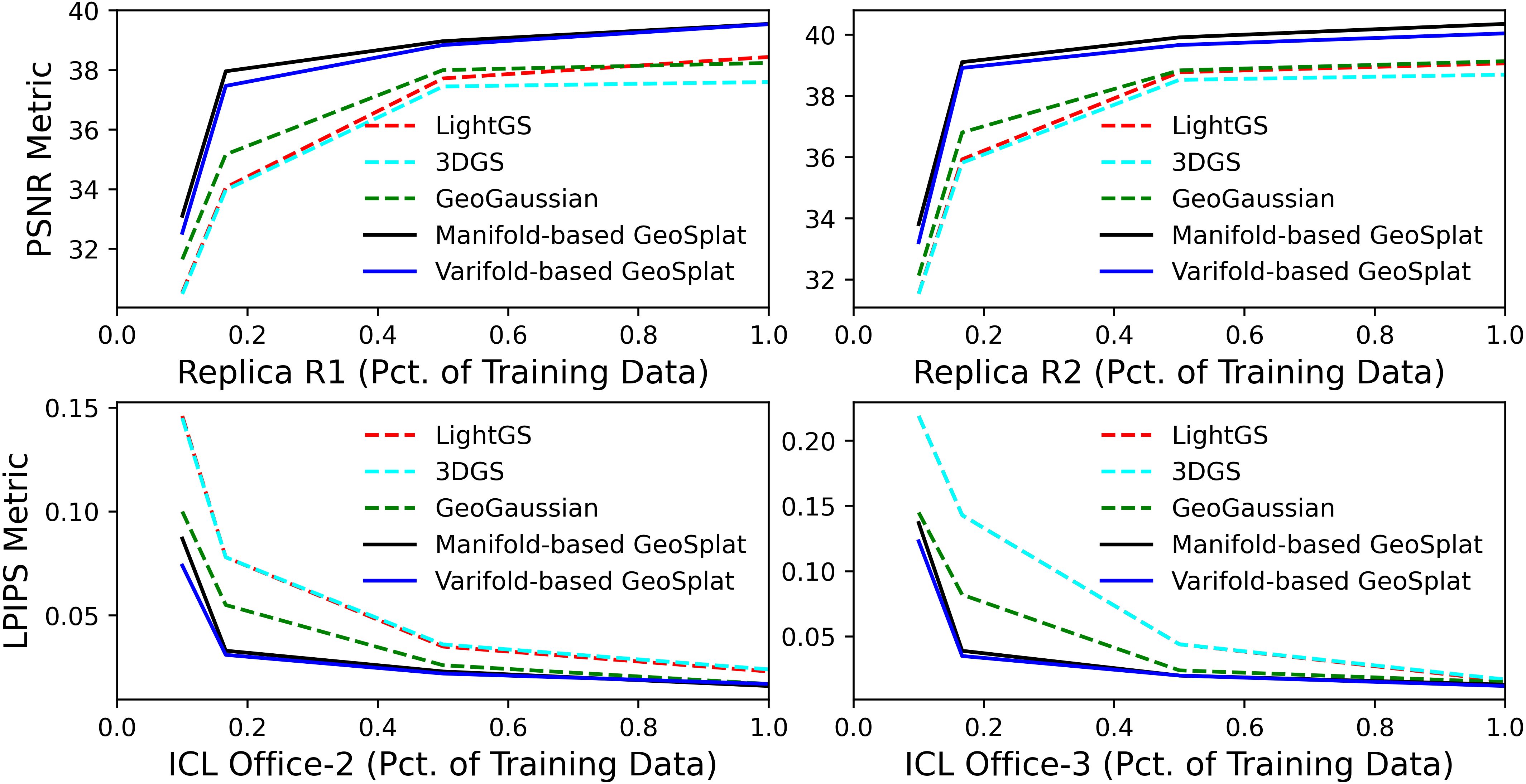
• Empirical evaluations demonstrate significant PSNR improvements on Replica and ICL datasets, validating the method's effectiveness in low-data regimes.

GeoSplat: Geometry-Constrained Gaussian Splatting for Enhanced 3D Scene Rendering

Introduction and Motivation

GeoSplat introduces a geometry-constrained optimization framework for 3D Gaussian splatting, targeting novel view synthesis. The method addresses two major limitations in prior works: (1) the reliance on low-order geometric priors (e.g., normals) and (2) the use of noise-sensitive, static estimation methods for geometric information. GeoSplat leverages both first-order (normals, tangents) and second-order (curvature) geometric quantities, integrating them into all stages of the Gaussian splatting pipeline: initialization, optimization, and densification. The framework is supported by robust, efficient estimation methods based on local manifold and varifold structures, enabling dynamic geometric priors throughout training.

Geometry-Constrained Optimization Framework

GeoSplat regularizes the entire Gaussian splatting pipeline using geometric information:

• Curvature-Guided Initialization: Covariance matrices of Gaussian primitives are initialized using principal curvatures and directions, ensuring tight surface coverage and anisotropic scaling aligned with local surface geometry. Specifically, the normal direction is assigned a minimal scale, while tangent directions are scaled inversely to curvature magnitudes, maintaining area invariance.
• Curvature-Guided Primitive Upsampling: Flat regions (low mean absolute curvature, MAC) are identified and populated with new primitives via midpoint interpolation, improving coverage and reducing holes in low-texture areas.
• Shape-Constrained Optimization: Gradient updates for primitive positions are truncated along the normal direction, mitigating floating artifacts and ensuring primitives remain attached to the underlying surface. Additional regularization terms enforce rank-2 covariance matrices and alignment of rotation matrices with principal directions, preventing degenerate (needle-like) shapes.
• Curvature-Regularized Densification: Split and clone operations for densification are geometrically constrained, interpolating new primitive positions along principal directions and limiting displacement in the normal direction, reducing outlier generation.

  Figure 1: The initial Gaussian primitives of Replica OFF2 are enriched through our curvature-guided primitive upsampling strategy. The points in red are newly added.

Noise-Robust Geometric Estimation

GeoSplat employs two complementary estimation strategies for geometric priors:

• Manifold-Based Estimation: Assumes local smoothness and computes tangent spaces and principal curvatures via eigendecomposition of kernel matrices derived from local neighborhoods. The approach leverages Laplacian-based Monte Carlo approximations for efficient operator estimation, supporting dynamic updates as the primitive cloud evolves.
• Varifold-Based Estimation: Utilizes weak second fundamental form (WSFF) matrices for curvature estimation, free from smoothness assumptions. This method is robust to sparsity and noise, directly operating on discrete primitive locations and tangent projections.

Both methods scale efficiently to millions of primitives, enabling periodic updates of geometric priors during training with minimal computational overhead.

Empirical Evaluation

GeoSplat is evaluated on Replica and ICL datasets for novel view synthesis, compared against baselines including 3DGS, GeoGaussian, LightGS, and others. Metrics include PSNR, SSIM, and LPIPS.

• Main Results: GeoSplat consistently outperforms baselines across all scenes. For example, on Replica R1, manifold-based GeoSplat achieves a PSNR improvement of 3.42% over GeoGaussian. On ICL Room-1, varifold-based GeoSplat yields a 2.77% PSNR gain over 3DGS.

  Figure 2: The performance of our models and baselines in low-resource settings.

• Low-Resource Regimes: GeoSplat demonstrates slower performance degradation as the number of observed views decreases, with PSNR gains increasing from 3.11% (full data) to 7.93% (1/6 views) on Replica R2.
• Qualitative Analysis: Rendered images and primitive clouds show that GeoSplat produces fewer floating artifacts and holes, especially in sparse-view scenarios, compared to both 3DGS and GeoGaussian.

Figure 3: Ground Truth (Case 1).

Figure 4: Baseline: 3DGS.

Figure 5: Ground Truth (Case 1).

Figure 6: Ground Truth (Case 1).

Figure 7: Ground Truth (Case 1).

Ablation Studies

Systematic ablations confirm the necessity of each geometric regularization component. Removing curvature-guided initialization, upsampling, truncated gradient updates, or shape regularization consistently degrades performance (e.g., PSNR drops by up to 1.07% on Replica R0 without shape regularization). Using MAC instead of mean curvature for flat-area identification yields superior upsampling results.

Theoretical and Practical Implications

GeoSplat demonstrates that incorporating high-order geometric priors (curvature) into Gaussian splatting yields measurable improvements in rendering fidelity, especially under data scarcity. The framework's robust estimation methods enable dynamic adaptation to evolving scene geometry, overcoming the limitations of static, noise-sensitive priors. The approach is compatible with existing low-order regularizations and can be integrated into other splatting-based pipelines.

From a theoretical perspective, the work bridges differential geometry and geometric measure theory (varifold) with practical 3D scene representation, providing analytical tools for curvature estimation in discrete settings. The use of MAC as a flatness criterion and the explicit covariance initialization formulas are notable contributions.

Future Directions

Potential extensions include:

• Integration with neural radiance field methods for hybrid representations.
• Application to non-smooth or highly non-manifold scenes using varifold-based priors.
• Exploration of higher-order geometric regularizations (e.g., torsion) and their impact on rendering.
• Real-time adaptation of geometric priors for online SLAM and dynamic scene reconstruction.

Conclusion

GeoSplat establishes a comprehensive geometry-constrained framework for 3D Gaussian splatting, leveraging both first- and second-order geometric information for improved scene coverage, artifact reduction, and rendering quality. The method's robust, efficient estimation strategies and dynamic regularization mechanisms set a new standard for geometry-aware scene synthesis, with strong empirical results and broad applicability to future 3D vision systems.