Why Language Models Hallucinate (2509.04664v1)
Abstract: Like students facing hard exam questions, LLMs sometimes guess when uncertain, producing plausible yet incorrect statements instead of admitting uncertainty. Such "hallucinations" persist even in state-of-the-art systems and undermine trust. We argue that LLMs hallucinate because the training and evaluation procedures reward guessing over acknowledging uncertainty, and we analyze the statistical causes of hallucinations in the modern training pipeline. Hallucinations need not be mysterious -- they originate simply as errors in binary classification. If incorrect statements cannot be distinguished from facts, then hallucinations in pretrained LLMs will arise through natural statistical pressures. We then argue that hallucinations persist due to the way most evaluations are graded -- LLMs are optimized to be good test-takers, and guessing when uncertain improves test performance. This "epidemic" of penalizing uncertain responses can only be addressed through a socio-technical mitigation: modifying the scoring of existing benchmarks that are misaligned but dominate leaderboards, rather than introducing additional hallucination evaluations. This change may steer the field toward more trustworthy AI systems.
Summary
- The paper demonstrates that hallucinations are natural statistical errors, formalized as misclassifications in the 'Is-It-Valid' (IIV) binary framework.
- It categorizes error sources such as epistemic uncertainty, model misspecification, computational hardness, distribution shift, and data quality issues.
- The study proposes modifying evaluation protocols to reward calibrated uncertainty and abstention, thereby mitigating overconfident guessing.
Statistical and Socio-Technical Causes of Hallucination in LLMs
The paper "Why LLMs Hallucinate" (2509.04664) provides a rigorous statistical and socio-technical analysis of hallucinations in LLMs. The authors argue that hallucinations—plausible but incorrect outputs—are not mysterious artifacts but are instead a natural consequence of the objectives and evaluation protocols used in modern LLM training and deployment. The work formalizes the connection between generative errors in LLMs and misclassification in supervised learning, and it critiques the prevailing evaluation methodologies that inadvertently incentivize overconfident guessing over calibrated uncertainty.
Formalizing Hallucination as a Statistical Error
The central thesis is that hallucinations in LLMs are fundamentally errors in binary classification, specifically in distinguishing valid from invalid outputs. The authors introduce the "Is-It-Valid" (IIV) binary classification problem, where the model must classify outputs as valid or erroneous. They show that the generative error rate of a LLM is lower-bounded by twice the IIV misclassification rate, modulo calibration and class imbalance terms. This reduction is illustrated in (Figure 1).
Figure 1: Is-It-Valid requires learning to identify valid generations using labeled examples (left). Classifiers (dashed lines) may be accurate on certain concepts like spelling (top) but errors often arise due to poor models (middle) or arbitrary facts when there is no pattern in the data (bottom).
This formalism demonstrates that even with error-free training data, the statistical objectives optimized during pretraining (e.g., cross-entropy minimization) will inevitably lead to some generative errors. The analysis is agnostic to model architecture and applies to both next-token prediction and general density estimation.
Taxonomy of Error Sources
The paper categorizes the statistical sources of hallucination:
- Epistemic Uncertainty (Arbitrary Facts): When facts are unpatterned and appear only once in the training data (e.g., rare birthdays), the model cannot generalize, and the hallucination rate is at least the singleton rate in the data.
- Model Misspecification: If the model class cannot represent the true data distribution (e.g., trigram models for long-range dependencies), high error rates are inevitable.
- Computational Hardness: For problems that are computationally intractable (e.g., cryptographic decryption), no efficient model can avoid errors.
- Distribution Shift: Out-of-distribution prompts induce errors due to mismatch between training and test distributions.
- GIGO (Garbage In, Garbage Out): Errors in the training data are replicated by the model.
The analysis is extended to prompted settings, where the model must generate valid responses conditioned on a prompt, and the same lower bounds on error rates apply.
Calibration and Its Limits
The authors show that calibration—matching predicted probabilities to empirical frequencies—is a natural outcome of cross-entropy minimization in pretraining. However, perfect calibration does not preclude hallucinations; in fact, a perfectly calibrated model will still hallucinate on unlearnable or rare facts. Empirical evidence from GPT-4 calibration histograms (Figure 2) supports this claim: pretraining yields well-calibrated models, but post-training (e.g., via RLHF) can distort calibration.
Figure 2: GPT-4 calibration histograms before (left) and after (right) reinforcement learning. The pretrained model is well calibrated.
Socio-Technical Drivers: Evaluation and Benchmarking
A key contribution is the identification of evaluation protocols as a major driver of persistent hallucinations. Most mainstream benchmarks use binary grading (correct/incorrect), awarding no credit for abstaining or expressing uncertainty (e.g., "I don't know"). This incentivizes models to guess when uncertain, as abstention is strictly suboptimal under these metrics. The authors formalize this with a simple observation: under binary grading, the optimal strategy is always to guess, never to abstain.
The paper surveys popular benchmarks and finds that nearly all penalize uncertainty, reinforcing overconfident guessing. Even hallucination-specific evaluations are insufficient if the primary benchmarks remain misaligned.
Mitigation: Realigning Evaluation Protocols
The authors propose a socio-technical mitigation: modify existing benchmarks to explicitly reward calibrated uncertainty. This can be achieved by:
- Explicit Confidence Targets: Incorporate confidence thresholds and penalties for incorrect answers, as in some standardized human exams. For example, only answer if confidence exceeds , with penalties for incorrect answers and zero credit for abstention.
- Behavioral Calibration: Evaluate models on their ability to abstain or hedge when uncertain, not just on accuracy.
Such modifications would realign incentives, encouraging models to express uncertainty appropriately and reducing the prevalence of hallucinations.
Implications and Future Directions
The theoretical results imply that hallucinations are an unavoidable consequence of statistical learning under current objectives and data regimes, especially for rare or unpatterned facts. However, the persistence and overconfidence of hallucinations are exacerbated by evaluation protocols that penalize uncertainty. The work suggests that meaningful progress on trustworthy AI requires not just technical advances in modeling, but also changes in how models are evaluated and benchmarked.
Future research directions include:
- Developing and adopting evaluation protocols that reward calibrated uncertainty and abstention.
- Exploring richer forms of uncertainty expression beyond "I don't know," such as hedging and clarification requests.
- Investigating the interplay between model architecture, training objectives, and behavioral calibration.
- Extending the statistical framework to open-ended and multi-fact generations, and to settings with latent or ambiguous context.
Conclusion
"Why LLMs Hallucinate" provides a principled statistical and socio-technical account of hallucinations in LLMs. The inevitability of generative errors is rooted in the fundamental limits of statistical learning, while the persistence of overconfident hallucinations is reinforced by misaligned evaluation protocols. Addressing hallucination thus requires both technical and institutional changes, particularly in how the field defines and rewards trustworthy model behavior.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Explain it Like I'm 14
What is this paper about?
This paper asks a simple question: Why do AI LLMs sometimes make up confident, believable answers that are wrong (often called “hallucinations”)? The authors argue that these mistakes aren’t mysterious. They mostly come from how we train and score models today, which quietly encourages guessing instead of saying “I don’t know.”
What questions do the authors ask?
- Why do LLMs produce believable false answers, even when they “should” say they’re unsure?
- Does this happen because of how we first train models on massive text (pretraining), or because of the later tuning to be helpful and safe (post‑training), or both?
- How do current tests and leaderboards push models to bluff?
- What practical changes would make models more honest and trustworthy?
How do they paper the problem?
The paper uses math and simple analogies rather than big experiments. Here’s the core idea in everyday terms.
A simple test: “Is-It-Valid?” (IIV)
Imagine you could turn any LLM into a yes/no tester that answers: “Is this response valid or not?” The authors show that:
- If a model can’t perfectly pass this simple yes/no test, then when it has to generate full answers, it will make mistakes.
- In fact, the model’s rate of making wrong generations is closely tied to how often it would fail the yes/no test. Roughly, if the model mislabels some percentage of cases in the simple test, it will make at least about twice that percentage of errors when producing full answers.
This connects “generation” (writing answers) to “classification” (yes/no decisions). Errors that are common in basic classification show up as hallucinations when the model writes.
Why pretraining alone still causes mistakes
Pretraining teaches a model to match the overall patterns of language (what words and sentences look like). Even if the training text were perfect and error‑free, that objective still leads to some wrong outputs because:
- Some facts just don’t have a learnable pattern (for example, random details like a lesser‑known person’s birthday). If the data doesn’t provide enough signal, the model can’t reliably learn them.
- The authors show a lower bound: if certain facts appear only once in the training data (so the model never sees them again), the model will often guess. In other words, the “hallucination rate” on those facts is at least as big as the fraction of such “one‑off” facts. Example: If 20% of birthday facts appeared only once in the data, expect at least about 20% wrong answers when asked those kinds of birthday questions.
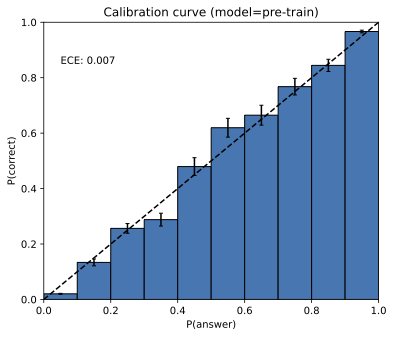
They also explain “calibration”: a calibrated model’s confidence should match reality (e.g., things it says with 70% confidence should be right about 70% of the time). The common pretraining objective (cross‑entropy) tends to push models toward calibration. Ironically, being well‑calibrated while trying to cover broad language patterns makes some mistakes unavoidable.
Why post‑training and exams can make things worse
After pretraining, we fine‑tune models to be helpful and pass benchmarks. But most benchmarks score like school tests: 1 point for correct, 0 for incorrect, and 0 for “I don’t know.” That grading makes guessing strictly better than admitting uncertainty. So:
- Models learn to bluff when unsure, because that wins more points.
- This keeps hallucinations alive, even if the model internally “knows” it’s not confident.
What did they find?
Here are the main takeaways, in plain language:
- Hallucinations naturally arise from the statistics of learning:
- If a model sometimes can’t tell valid from invalid answers in a simple yes/no check, it will make mistakes when generating full answers.
- For “arbitrary facts” (like random birthdays) that don’t repeat in the data, models will often guess. The more one‑off facts in the training set, the more hallucinations you should expect on that type of question.
- Being a “good test‑taker” under today’s binary grading (right/wrong only) rewards guessing over honesty. That’s a big reason hallucinations persist after post‑training.
- Some errors come from limited model designs (for example, old‑style models that only look at a couple of words at a time can’t capture long‑range grammar rules), from hard problems (some questions are computationally tough), from out‑of‑distribution prompts (weird questions the model rarely saw), and from bad data (garbage in, garbage out).
- It’s not that hallucinations are inevitable for every possible system. A tool‑using or lookup‑based system could say “I don’t know” for anything it can’t verify. But a general LLM trained to match broad language patterns—and graded like a multiple‑choice test—will produce some confident mistakes.
Why this matters:
- It explains a stubborn real‑world problem in a clear, general way.
- It shows that simply adding more training data or tinkering with decoding may not fix the core issue.
- It points to the evaluation rules (how we score models) as a major driver of overconfident mistakes.
What do they propose to fix it?
The authors suggest a socio‑technical change: don’t just invent more “hallucination tests.” Instead, change the scoring of existing, popular benchmarks so they stop punishing uncertainty.
- Add explicit confidence targets to prompts on mainstream benchmarks:
- Tell the model: “Only answer if you’re more than t‑percent confident. A wrong answer loses t/(1−t) points. ‘I don’t know’ is 0 points.”
- Examples: t = 0.5 (penalty 1), t = 0.75 (penalty 2), t = 0.9 (penalty 9).
- With this rule, it’s better to say “I don’t know” when you’re not confident, and better to answer only when you are.
- Make these rules part of the instructions so behavior is unambiguous and fairly graded.
- Use these confidence‑aware rules in the big leaderboards that everyone already cares about. That way, models will be rewarded for honest uncertainty, not punished for it.
The authors also introduce “behavioral calibration”: instead of reporting a number like “72% confident,” the model should simply choose to answer or abstain in a way that matches the stated confidence threshold. This is easier to evaluate fairly and encourages the right behavior.
Key terms in simple words
- Hallucination: A confident, believable answer that’s wrong.
- Pretraining: The first phase of training on huge amounts of text to learn language patterns.
- Post‑training: Extra training to make the model helpful, safe, and better at tests.
- Calibration: Matching confidence to reality (e.g., when you say “I’m 80% sure,” you’re right about 80% of the time).
- Benchmark/Leaderboard: Standard tests and rankings used to compare models.
- “Is‑It‑Valid?” (IIV): A simple yes/no check—does a response look valid or not?
- Singleton rate: How often a specific fact appears only once in the training data; a signal that the model can’t learn that fact reliably.
- Distribution shift: When test questions look different from the training data.
- Garbage in, garbage out (GIGO): If training data contains errors, models can learn and repeat them.
Limitations and what’s next
- This is a theory‑heavy paper: it builds a careful argument rather than running lots of new experiments. Real systems can have extra tricks (like search tools) that change behavior.
- Fixing hallucinations isn’t just about one new metric; it needs community adoption—changing how popular tests score answers.
- Still, the plan is practical: clearly state confidence rules in benchmark prompts and adjust scoring so “I don’t know” is sometimes the best, most honest choice.
Bottom line
LLMs often “hallucinate” because:
- Pretraining makes some errors unavoidable, especially for rare or random facts.
- Post‑training benchmarks reward guessing under right/wrong scoring.
The fix isn’t only better models—it’s better scoring. If we change today’s popular evaluations to reward honest uncertainty, we can steer models toward being more trustworthy, careful, and aligned with how we actually want them to behave.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of what remains missing, uncertain, or unexplored in the paper, framed to guide concrete follow-up research.
- Empirical validation of theory-to-practice: The reduction from generation to IIV classification and the derived lower bounds (e.g., err ≥ 2·IIV error − terms) lack large-scale empirical validation across modern LLM families, datasets, and decoding regimes.
- Realism of the “uniform error” assumption: The IIV construction samples errors uniformly from the error set E (and uses 50/50 mixes), which is unlikely to reflect real error distributions; quantify how non-uniform or structured error distributions alter the bounds or the reduction.
- Finite plausibility set assumption: The analysis relies on a finite plausible string set X and known |E_c|; operationalizing X and estimating |E_c| for open-ended, long-form text remains undefined and may be infeasible in practice.
- Calibration term δ scope: The δ measure is defined at a single threshold t = 1/|E|, weaker than ECE; develop theoretically principled and practically auditable multi-threshold or sequence-level calibration criteria that retain the reduction’s guarantees.
- Cross-entropy ⇒ calibration claim: The argument that cross-entropy optimization yields small δ is heuristic; formalize conditions (model class properties, optimization behavior, early stopping, label smoothing) under which δ is provably small, and test empirically.
- Impact of token-level vs sequence-level training: The analysis abstracts away next-token training; quantify how token-level teacher forcing, exposure bias, and decoding compose to sequence-level generative error rates predicted by the reduction.
- Decoding effects: The role of temperature, top-k/p sampling, nucleus sampling, and beam search on hallucination rates and calibration is not modeled; characterize how decoding strategies modulate the derived lower bounds and abstention behavior.
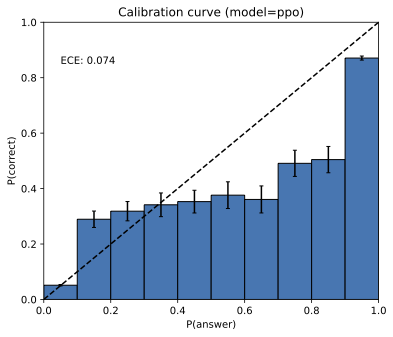
- Post-training calibration drift: The paper highlights calibration changes post-RL (e.g., GPT-4 PPO) but lacks a systematic paper; measure when, how, and why post-training breaks or restores calibration across tasks and models.
- Noisy and partially wrong training data (GIGO): The theoretical results assume p(V) = 1; extend the framework to explicit noise models (random/class-conditional/correlated label noise, partial truths) and derive tight bounds on generative errors under noise.
- Retrieval-augmented and tool-using systems: Although claimed to apply broadly, there is no formal treatment of RAG/tools; model retrieval noise, document trustworthiness, tool error, and time-varying knowledge, and extend theorems to these pipelines.
- Multi-turn interaction: The analysis treats single-turn prompt–response; extend to multi-turn dialogues where uncertainty can be reduced via clarification questions, and paper incentives under benchmarks that price/penalize clarification.
- Open-ended evaluation scoring: The proposal focuses on binary-to-penalized abstention; develop principled scoring for open-ended, LM-graded or rubric-based tasks that avoid rewarding bluffs and allow abstentions without collapsing coverage.
- Confidence-target adoption: The socio-technical recommendation (explicit confidence thresholds t) lacks empirical studies on adoption barriers, user acceptance, and leaderboard impacts; run controlled trials with organizers to measure feasibility and side effects.
- Choosing and calibrating t: Provide normative and domain-specific guidance for setting threshold t (e.g., risk-based, stakeholder-driven), including per-task heterogeneity and fairness across languages and domains.
- Behavioral calibration auditing: Define robust, reproducible audits for “behavioral calibration” (coverage–accuracy curves vs t) and specify pass/fail criteria that are hard to game with templated IDK strategies.
- Preventing gaming under LM graders: LM-based graders can be fooled by confident bluffs; design verifiable graders (symbolic checkers, reference-based equivalence, adversarial rubric stress tests) resistant to stylistic overconfidence.
- Selective prediction theory bridge: Connect the results explicitly to selective classification/conformal prediction; develop actionable selective-generation training objectives with coverage guarantees and abstention calibration.
- Trade-offs with breadth/diversity: The paper cites inherent breadth–consistency trade-offs but does not quantify how explicit abstention scoring shifts this frontier; characterize Pareto curves among breadth, abstention rate, and hallucinations under different t.
- Measuring singleton rates in-the-wild: Theorem-driven claims about singleton rates (sr) need measurement across fact types (biographies, science, code APIs) in modern corpora; build pipelines to estimate sr and correlate with hallucination rates.
- Tokenization-induced failures: The letter-counting example hints at tokenization issues; systematically analyze how tokenization schemes influence hallucination classes (character-level, morphology, numeracy) and propose mitigations.
- Distribution shift formalization: Provide distribution-shift-aware bounds (covariate, label, concept shift) for generative errors, and practical OOD detectors tied to abstention policies that preserve coverage–accuracy guarantees.
- Complexity barriers and refusal policy: For computationally hard queries, specify principled refusal/IDK policies and tool fallback strategies; analyze user experience trade-offs and how benchmarks should grade such refusals.
- Defining plausibility in practice: The boundary between “plausible” and “nonsense” outputs is assumed but not operationalized; propose practical criteria or detectors (fluency, syntax, semantics) to construct X and evaluate sensitivity to this choice.
- Multiple correct answers and equivalence classes: Extend the analysis and scoring to prompts with many semantically equivalent correct answers; specify matching/equivalence mechanisms that don’t penalize cautious under-specification.
- Confidence communication beyond IDK: The paper references graded uncertainty language but does not integrate it into scoring; design and validate rubrics that reward calibrated hedging and evidence-citing without incentivizing verbosity.
- Interaction with safety alignment: Analyze conflicts between abstention incentives and safety refusals (e.g., over-refusal); propose joint objectives and evaluations that separate safety-driven refusals from uncertainty-driven abstentions.
- Accessibility and multilinguality: Investigate how confidence-target instructions and abstention lexicons transfer across languages/cultures, and how graders reliably recognize IDK/hedges multilingualy.
- Practical computation of p̂(r|c): The reduction assumes access to sequence-level probabilities for thresholding; detail how to approximate or proxy p̂(r|c) for long generations and how approximation error affects bounds and audits.
- Effects of continual/online learning: Study how ongoing fine-tuning, retrieval updates, and tool improvements shift calibration, singleton rates, and hallucination incidence over time.
- Benchmark coverage and representativeness: The meta-evaluation of benchmark scoring policies is limited; conduct a comprehensive survey across domains (STEM, legal, medical, coding, multilingual) and publish a standardized taxonomy and scoring recommendations.
- User-centered thresholding: Explore adaptive thresholds t conditioned on user-stated risk tolerance or task criticality; design interfaces and scoring that faithfully elicit and enforce such preferences.
- Cost of clarification and abstention: Quantify utility trade-offs when models abstain or ask clarifying questions (latency, user effort), and design benchmarks that incorporate these costs transparently.
- Verification-first pipelines: Examine whether integrating verification (self-check, external search, tool use) before answering can reduce hallucinations without sacrificing calibration; compare against abstention-only strategies under confidence targets.
- Formal integration of prompts with IDK sets: The framework assumes known abstention sets A_c; specify practical corpora or schema for standardizing abstention phrases and preventing false positives in grading.
Conceptual Simplification
Core Contributions in Plain Language
Big picture
The paper gives a simple, statistical explanation for why LLMs produce confident but false statements (“hallucinations”), and why these errors persist even after post-training. The key insight is that both training objectives and today’s evaluation practices unintentionally reward guessing over “I don’t know,” making hallucinations a predictable outcome—not a mysterious failure of neural networks.
1) A simple reason hallucinations arise in pretraining
Pretraining tries to fit a model to the distribution of text. Even if the training text were perfectly accurate, a well-trained model will still make some errors when generating new text. Intuitively, generation is harder than deciding whether a candidate answer is valid: to generate a response, the model must implicitly “decide validity” across many possible strings and then pick one.
The paper formalizes this by reducing generation to a binary “Is-It-Valid?” (IIV) classification task: for any LLM, you can build a validity classifier by thresholding its probabilities. This yields a direct inequality:
- Roughly, generative error rate ≥ 2 × IIV misclassification rate (up to small terms).
The takeaway: the same statistical forces that cause classification errors (limited data, unlearnable patterns, model mismatch, distribution shift) also cause generative errors—including hallucinations—in base LLMs.
2) Calibration connects standard pretraining to inevitable errors
Modern pretraining minimizes cross-entropy. This tends to make base models calibrated in a simple sense: the mass they assign to “likely” strings matches the mass seen in data. The paper shows that if a base model is (even weakly) calibrated, then the IIV→generation reduction implies a nontrivial lower bound on its generative error rate. In contrast, a model that never errs could either be degenerate (always outputs “I don’t know”) or miscalibrated (assigns probabilities in a way that doesn’t match the data). So, for realistic, well-trained base models, some errors are not a bug; they’re a statistical consequence of the objective.
This argument does not depend on Transformers or “next-word prediction” per se; it applies to density estimation broadly.
3) Quantitative predictions for two common sources of hallucination
The framework yields concrete, testable predictions in two stylized but important cases.
- Arbitrary facts (epistemic uncertainty). For facts with no learnable pattern (e.g., specific birthdays), the best you can do with finite data is limited by how often the fact appears. The paper recovers and strengthens prior results: if a sizable fraction of facts appear only once in pretraining (the “singleton rate”), then base models should hallucinate on at least that fraction of queries about such facts (up to small terms). This ties hallucinations to Good–Turing “missing mass” intuition: a lot of one-offs means a lot of unknowns remain, so guesses are frequent.
- Poor models (representation/optimization limits). If the model family cannot represent the needed structure well (e.g., old n-gram models missing long-range agreement), the best achievable classification error is high, and thus the generative error must also be high. The paper illustrates this with classic examples (like trigrams failing on gender agreement or tokenization blocking letter-counting) and proves lower bounds in a clean multiple-choice scenario.
These results extend to prompted settings (questions plus answers), not just unprompted generation.
4) Prompts are handled explicitly
The analysis generalizes to realistic query–response settings where each prompt has a set of plausible answers, some valid and some erroneous (including “I don’t know” as a valid abstention). The same reduction and bounds go through, showing the conclusions aren’t an artifact of unprompted text modeling.
5) Why post-training doesn’t eliminate hallucinations
Even though post-training tries to reduce hallucinations, many benchmarks and leaderboards score with binary right/wrong metrics. Under such scoring, abstaining (IDK) is strictly suboptimal: a model that always “guesses” when unsure will, in expectation, outperform an equally knowledgeable model that honestly abstains when uncertain. This is the test-taking effect: if blanks get zero and correct answers get one, guessing dominates.
The consequence: when optimization is driven by these benchmarks, models learn to be good test-takers—confident and specific—even when unsure. This creates a field-wide incentive structure that reinforces hallucinations.
6) A practical, socio-technical fix: change how we score
Instead of inventing yet more specialized hallucination tests, the paper argues for modifying the scoring rules of mainstream evaluations so they stop penalizing appropriate uncertainty. The proposal is simple and actionable:
- Put explicit confidence targets into the instructions. For example: “Answer only if you are >t confident; a wrong answer costs t/(1–t) points; ‘I don’t know’ earns 0.” Reasonable thresholds include t = 0.5, 0.75, 0.9. This makes the optimal behavior crystal clear and auditable.
- Apply this to the primary benchmarks (e.g., coding, math, QA) that currently drive the leaderboard. Once abstention is fairly treated, models that guess less when unsure won’t be punished, and training can align toward trustworthy behavior.
A nice side effect: this promotes “behavioral calibration.” Without asking models to output numeric probabilities, they learn to answer only when their internal chance of being right exceeds the stated threshold. This can be checked by measuring accuracy and abstention rates across thresholds.
7) What this does and does not claim
- Hallucinations are not inherently unavoidable in principle. You can build narrow systems that answer a fixed set of questions perfectly and say “I don’t know” otherwise.
- The claim is that for general-purpose base models trained with standard objectives and evaluated with binary scoring, hallucinations are statistically expected and strategically rewarded.
- The analysis also clarifies other contributors (computational hardness, distribution shift, and “garbage in, garbage out”): the same classification-to-generation lens captures these, too.
Takeaways
- Pretraining alone produces some errors for statistical reasons; that includes hallucinations.
- The paper’s reduction shows generation inherits the same error drivers as binary classification.
- For “arbitrary facts,” the fraction of one-off facts in data predicts a floor on hallucinations.
- For “poor models,” representational limits impose lower bounds on errors.
- Post-training doesn’t fully fix hallucinations because most benchmarks reward guessing.
- The proposed remedy is to modify scoring on mainstream benchmarks with explicit confidence thresholds, so models are incentivized to abstain when unsure and be trustworthy by default.
Future Research Directions
Summary of opportunity
This paper reframes hallucinations as a statistical consequence of modern training and evaluation: a reduction from generation to binary “Is-It-Valid” (IIV) classification yields lower bounds linking generative error to misclassification and calibration; “arbitrary facts” produce irreducible errors tied to singleton rate; poor model classes induce agnostic error; and post‑training plus binary grading incentivizes guessing rather than abstention. These findings suggest concrete empirical tests, theory extensions, system designs, and socio‑technical changes to benchmarks.
Empirical studies to validate and stress‑test the theory
The following experiments would directly probe the paper’s claims and quantify practical impact.
- Measure the reduction empirically across domains. Construct IIV testbeds where valid strings come from curated corpora and invalid strings are uniformly sampled within plausible formats. For a range of base models and prompts:
- Estimate IIV error and generative error; test the lower bound tightness and the role of the calibration term at the threshold .
- Compare across decoding strategies (greedy, temperature, nucleus); test whether decoding that concentrates mass above/below the threshold tracks the predicted error changes.
- Calibrational audit at the critical threshold. Using held‑out and , estimate the paper’s calibration deviation for . Test:
- Does standard cross‑entropy training drive as predicted?
- How do RLHF/RLAIF/DPO and instruction‑tuning shift relative to base pretraining?
- Arbitrary‑facts scaling law via singleton rate. Build a controlled “canonical‑form facts” dataset (e.g., fixed‑format birthdays, ISBN–title pairs, synthetic key–value facts). Pretrain/fine‑tune comparable models on varying sample sizes and measure:
- Singleton rate in the training set and out‑of‑sample hallucination rate on unseen prompts, testing the bound in Theorem 4.
- How and hallucinations evolve under data deduplication and cite‑count reweighting.
- Poor‑model factor with controlled context dependence. Create minimal pairs requiring long‑range or structural dependencies (e.g., gender agreement, letter counting, cross‑sentence co‑reference), then compare:
- Models with and without reasoning modules (e.g., DeepSeek‑R1‑like vs non‑reasoning) to quantify reductions in the effective agnostic error term .
- Tokenization effects (character‑aware vs BPE‑only) on letter‑counting hallucinations.
- Distribution shift and computational hardness. Evaluate:
- OOD prompts with explicit “IDK allowed” instructions; quantify abstention behavior and violations under binary scoring vs confidence‑target scoring.
- Cryptographic/decryption prompts where IDK is valid; test whether models trained with confidence targets abstain more reliably.
- Behavioral calibration evaluation. For each benchmark and for thresholds , prompt with explicit confidence targets (see below) and plot risk–coverage curves:
- Coverage and selective accuracy ; compute area under risk–coverage (AURC).
- A monotonicity check: as increases, coverage should fall and conditional accuracy should rise.
- Post‑training incentive experiment at scale. On widely used benchmarks (e.g., GPQA, MMLU‑Pro, SWE‑bench, Omni‑MATH), run A/B/C scoring:
- A: original binary grading.
- B: explicit confidence target with penalty for errors and 0 for IDK (tuned across ).
- C: risk–coverage aggregation across multiple .
- Measure how models adapt responses (bluffing vs abstaining), and quantify shifts in leaderboard ordering.
Theory extensions and formal analyses
Several directions could deepen and generalize the theoretical results.
- Tightening and generalizing the IIV–generation bound.
- Replace with learned or data‑dependent thresholds; derive bounds under soft plausibility sets and infinite output spaces.
- Remove or refine the calibration term by linking to stronger calibration notions (e.g., ECE) and Neyman–Pearson style optimal tests based on density ratios.
- Selective prediction with abstention. Connect the generation setting to selective classification:
- Define selective risk and paper regret bounds for policies that abstain unless .
- Derive guarantees for “behavioral calibration” under deviations from perfect knowledge of .
- Noisy training data (GIGO). Extend the bounds when :
- Agnostic versions of Theorem 3 with label noise and semi‑parametric identifiability assumptions; quantify how noise inflates hallucination lower bounds.
- Use Good–Turing style estimators under noise to predict hallucination as a function of novel‑fact mass.
- Domain adaptation. When train/test prompt distributions differ (), bound error via covariate shift terms (e.g., density ratio ) and IIV error under reweighting.
- Retrieval and tools as abstention surrogates. Model a two‑stage policy that either abstains, retrieves/tools, or answers:
- Optimize expected utility with retrieval cost; derive conditions where retrieval strictly dominates guessing.
- Provide coverage–risk–cost trade‑offs and sample complexity for learning the gating policy.
- Strategic benchmark game theory. Formalize the incentive misalignment:
- Model developers optimizing utility under competing leaderboards; show equilibria where binary grading induces guessing.
- Show that introducing explicit confidence targets can eliminate strictly dominated strategies (bluffing when ) and admit truthful equilibria.
Benchmark and evaluation redesign
To translate the socio‑technical recommendations into practice, concrete artifacts are needed.
- Confidence‑targeted versions of mainstream benchmarks. Release drop‑in scoring kits for GPQA, MMLU‑Pro, SWE‑bench, Omni‑MATH, etc., that:
- Append an instruction: “Answer only if your probability of being correct exceeds ; a wrong answer yields points; IDK yields 0 points.”
- Aggregate scores across a grid of values (e.g., 0, 0.5, 0.75, 0.9) and report both per‑ scores and AURC.
- New leaderboard primitives.
- Selective accuracy curves, coverage at fixed target risks, and “precision‑first” composites that weight correctness more than coverage.
- A standardized “behavioral calibration” test: for each , verify that empirical accuracy among answered items exceeds by a margin, with hypothesis tests and CIs.
- Robust graders and plausibility sets.
- For structured outputs (math/code), prefer equivalence checkers and unit tests over LM graders, and explicitly list abstention strings in .
- For LM‑graded tasks, include adversarial bluff checks and double‑adjudication to limit false positives.
Training and inference methods inspired by the framework
The paper implies concrete ways to reduce hallucinations while preserving capability.
- Abstention‑aware objectives. Incorporate utilities consistent with confidence targets during post‑training:
- Preference optimization with negative reward for incorrect answers and neutral reward for explicit IDK at sub‑threshold confidence.
- Offline DPO or RLHF variants that condition on (sampled per prompt) to teach the family of behaviors.
- Validity filters and rejection sampling. Train lightweight IIV validators that score or detect conflicts; at inference:
- Reject samples below a threshold or trigger retrieval/clarification.
- Calibrate the rejection threshold using conformal methods to achieve target error rates with finite‑sample guarantees.
- Architectural support for abstention. Provide native “IDK heads” or gating modules that jointly optimize coverage and selective risk, and reasoners that can “think more” before crossing the answer threshold.
- Data curation to lower singleton load. Deduplicate and upsample “arbitrary facts” that are singletons; add canonical phrasing to reduce ; evaluate the causal effect on hallucination rates predicted by the singleton bound.
Applications and field deployments
The following applications could stress‑test the approach in realistic, high‑stakes settings.
- Healthcare, legal, and finance copilots. Wrap models with confidence‑target prompts and abstention policies; log coverage and selective accuracy against human adjudication. Evaluate harm reduction vs throughput.
- Coding assistants (SWE‑bench and live repositories). Introduce risk‑aware patch suggestions with explicit abstentions and automated minimal‑repro scripts. Track fix‑rate, revert‑rate, and AURC over time.
- Enterprise search and RAG. Gate “final answers” behind thresholds; route low‑confidence queries to retrieval or human review. Quantify utility net of retrieval cost using the proposed utility function.
Data and corpus science
To understand and predict hallucination rates, corpus‑level measurements are needed.
- Estimate singleton rates by fact type across major pretraining corpora (Common Crawl variants, books, code) and correlate with hallucinations by domain.
- Track how changes with scale and deduplication; project expected hallucination reduction from additional curated data vs model scaling.
Limitations and open questions to address
A few gaps offer additional avenues for research.
- Operationalizing plausibility sets at scale without LM grader bias.
- Handling multi‑ground‑truth and paraphrase explosion when enumerating and defining the threshold.
- Making the calibration term computable and actionable in very large output spaces; exploring density‑ratio proxies from discriminators.
- Characterizing when reasoning reduces without causing overfitting or new bluff modes.
Suggested artifacts to accelerate adoption
To catalyze the socio‑technical shift, the community would benefit from the following open resources.
- A “Selective Benchkit” with:
- Prompt templates injecting explicit confidence targets.
- Scorers for per‑ selective accuracy, risk–coverage, and AURC with uncertainty quantification.
- Baselines (vanilla vs abstention‑aware) across popular models.
- An “IIV Probe Suite”:
- Datasets and scripts to measure IIV vs generation errors and the calibration term.
- Tools to estimate singleton rates and predict hallucinations via Good–Turing‑style estimators.
- A living leaderboard that reports both traditional scores and selective metrics, demonstrating that abstention can be rewarded without sacrificing capability.
By combining these empirical tests, theoretical generalizations, and benchmark reforms, the community can move from explaining hallucinations to systematically reducing them—incentivizing models that are not just capable, but also trustworthy in how and when they answer.
Strengths and Limitations
Summary of strengths and limitations
This paper offers a unifying theoretical account of why LMs hallucinate and a socio-technical proposal to mitigate them by realigning evaluation. Its contributions span a general reduction from generation to classification, lower bounds that clarify when errors are unavoidable, and a practical blueprint for benchmark design that rewards calibrated abstention.
The following points highlight its main strengths and limitations across practical effectiveness, theoretical soundness, and potential blind spots.
Strengths
- General, architecture-agnostic theory: Reduces generative validity to an “Is-It-Valid” (IIV) binary classification task and proves lower bounds linking generative error to misclassification, with and without prompts, and with explicit treatment of IDK.
- Clear causal decomposition: Distinguishes pretraining inevitabilities (calibrated density estimation implies some errors) from post-training incentives (binary grading rewards guessing), grounding both in standard learning theory.
- Tight, interpretable bounds: Results such as err ≥ 2·(IIV error) − terms, extensions to multiple choice, and explicit prompt-dependent bounds make assumptions and constants transparent; connections to VC dimension and Good–Turing (singleton rate) yield intuitive predictions (e.g., arbitrary facts like birthdays).
- Calibration insight: Shows why cross-entropy encourages (local) calibration and explains why base models can be both calibrated and error-prone—clarifying empirical observations (e.g., GPT-4 pre- vs post-RL calibration).
- Actionable evaluation fix: Proposes explicit confidence targets with graded penalties, enabling “behavioral calibration” audits and aligning mainstream benchmarks with uncertainty-aware behavior without inventing new bespoke tests.
- Broad error taxonomy: Relates hallucinations to known error sources—epistemic uncertainty, poor inductive biases, computational hardness, distribution shift, and GIGO—linking to established ML theory and practice.
Limitations and blind spots
- Idealized distributions and thresholds: IIV uses a 50/50 mix and uniform errors, finite plausible sets, and thresholds like 1/|E|; mapping these to open-ended, paraphrastic, multi-modal outputs can be nontrivial, and |E_c| may be undefined in practice.
- Arbitrary-facts model simplifications: Assumes single canonical answers and independence across prompts; real tasks have synonyms, compositional answers, tool use, and retrieval that alter difficulty and error rates.
- Calibration assumption after pretraining: The argument that δ is small relies on local optimality and simple rescalings under cross-entropy; post-training often breaks calibration, and measuring δ reliably at scale is nontrivial.
- Lower bounds, not training recipes: Results explain inevitability but do not provide constructive algorithms to reduce hallucinations beyond changing evaluation incentives; quantitative predictions may be loose in complex settings.
- Evaluation proposal adoption risk: Success hinges on community uptake; penalties may induce over-abstention or strategic behavior, especially with LM graders or vague rubrics; real-world utility sometimes favors helpful breadth over conservative abstention.
- Limited empirical validation: Apart from illustrative anecdotes and prior calibration plots, the paper offers little large-scale empirical testing of predictions (e.g., singleton-rate-based forecasts) or of the net impact of confidence-targeted scoring on established leaderboards.
- Partial coverage of other drivers: Factors like decoding choices, adversarial prompting, instruction violations, tool failures, and retrieval quality are acknowledged but not modeled in depth; mitigation beyond evaluation redesign remains under-specified.
Overall, the paper’s main strength is a clean, theoretically grounded reduction that demystifies hallucinations as statistically expected errors under standard objectives, plus a concrete, testable path to realign incentives via confidence-targeted scoring. Its main limitations stem from idealized assumptions, reliance on community adoption for practical impact, and limited empirical substantiation of the proposed evaluation changes at scale.
Collections
Sign up for free to add this paper to one or more collections.