Towards a Unified View of Large Language Model Post-Training (2509.04419v1)

Abstract: Two major sources of training data exist for post-training modern LLMs: online (model-generated rollouts) data, and offline (human or other-model demonstrations) data. These two types of data are typically used by approaches like Reinforcement Learning (RL) and Supervised Fine-Tuning (SFT), respectively. In this paper, we show that these approaches are not in contradiction, but are instances of a single optimization process. We derive a Unified Policy Gradient Estimator, and present the calculations of a wide spectrum of post-training approaches as the gradient of a common objective under different data distribution assumptions and various bias-variance tradeoffs. The gradient estimator is constructed with four interchangeable parts: stabilization mask, reference policy denominator, advantage estimate, and likelihood gradient. Motivated by our theoretical findings, we propose Hybrid Post-Training (HPT), an algorithm that dynamically selects different training signals. HPT is designed to yield both effective exploitation of demonstration and stable exploration without sacrificing learned reasoning patterns. We provide extensive experiments and ablation studies to verify the effectiveness of our unified theoretical framework and HPT. Across six mathematical reasoning benchmarks and two out-of-distribution suites, HPT consistently surpasses strong baselines across models of varying scales and families.

• The paper demonstrates that SFT and RL integration can be unified via the Unified Policy Gradient Estimator (UPGE), enabling joint optimization.
• It introduces the hybrid post-training algorithm 'black' that adaptively balances SFT and RL signals based on real-time model performance.
• Empirical results show that 'black' outperforms standard baselines on diverse LLM benchmarks, enhancing exploration and generalization.

Unified Policy Gradient Estimator for LLM Post-Training

Introduction

The paper "Towards a Unified View of LLM Post-Training" (2509.04419) presents a comprehensive theoretical and empirical framework for understanding and improving post-training algorithms for LLMs. The authors demonstrate that Supervised Fine-Tuning (SFT) and Reinforcement Learning (RL) are not fundamentally distinct, but rather can be subsumed under a single optimization objective. This unification is formalized through the Unified Policy Gradient Estimator (UPGE), which decomposes the gradient calculation into four modular components: stabilization mask, reference policy denominator, advantage estimate, and likelihood gradient. Building on this framework, the paper introduces Hybrid Post-Training (HPT, referred to as "black"), an adaptive algorithm that dynamically balances SFT and RL signals based on real-time model performance.

Figure 1: Illustration of the Unified Policy Gradient Estimator, highlighting the modular decomposition into stabilization mask, reference policy denominator, advantage estimate, and likelihood gradient.

Theoretical Framework: Unified Policy Gradient Estimator

The central theoretical contribution is the derivation of the UPGE, which expresses the gradient of a broad class of post-training objectives as:

$$\mathrm{grad}_{uni} = \mathbb{1}_{stable} \frac{1}{\pi_{ref}} \hat{A} \nabla \pi_\theta$$

where:

• $\mathbb{1}_{stable}$ is a stabilization mask (e.g., PPO-style clipping),
• $\pi_{ref}$ is the reference policy denominator (current, rollout, or constant),
• $\hat{A}$ is the advantage estimate (fixed, normalized, or token-level),
• $\nabla \pi_\theta$ is the likelihood gradient.

This formulation subsumes SFT, PPO, GRPO, REINFORCE, and various offline/online RL algorithms. The authors show that all these methods optimize a common objective:

$$\mathcal{J}_\mu(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}[r(\tau|q)] - \mu\,\mathrm{KL}(\pi_\beta \| \pi_\theta)$$

where the KL term enforces adherence to demonstration data. The gradient of this objective naturally splits into RL and SFT components, which can be jointly optimized without intrinsic conflict.

Component Analysis and Bias-Variance Tradeoffs

The paper provides a detailed analysis of each UPGE component:

• Stabilization Mask: Controls gradient propagation for stability (e.g., PPO clipping, CISPO masks). Aggressive clipping reduces variance but may introduce bias.
• Reference Policy Denominator: Importance sampling via $\pi_{ref}$; choice depends on data source (on-policy, off-policy, or demonstration). Incorrect specification can lead to bias or instability.
• Advantage Estimate: Sequence-level or token-level, fixed or normalized. Normalization (e.g., GRPO) reduces variance but may introduce difficulty bias.
• Likelihood Gradient: Standard backpropagation through the policy network.

The authors argue that different instantiations of these components yield different bias-variance tradeoffs, and that optimal post-training requires dynamic adaptation rather than static choices.

Hybrid Post-Training Algorithm (black)

Motivated by the unified framework, the paper introduces "black" (HPT), which adaptively switches between SFT and RL based on per-question rollout accuracy. The algorithm computes a mixed loss:

$$\mathcal{L} = \alpha \mathcal{L}_{RL} + \beta \mathcal{L}_{SFT}$$

where $\alpha$ and $\beta$ are determined by the model's performance on sampled trajectories. If the model's accuracy on a question exceeds a threshold $\gamma$, RL is emphasized; otherwise, SFT is used. This gating mechanism enables efficient exploitation of demonstration data for weak models and stable exploration for strong models.

Empirical Results

Extensive experiments are conducted on Qwen2.5-Math-7B, Qwen2.5-Math-1.5B, and LLaMA3.1-8B across six mathematical reasoning benchmarks and two out-of-distribution suites. Key findings include:

• black consistently outperforms SFT, GRPO, SFT$\rightarrow$GRPO, LUFFY, and SRFT baselines.
• On Qwen2.5-Math-7B, black achieves a 7-point gain over the strongest baseline on AIME 2024.
• The adaptive mixing of SFT and RL yields superior Pass@k performance, especially for large $k$, indicating enhanced exploration capacity.

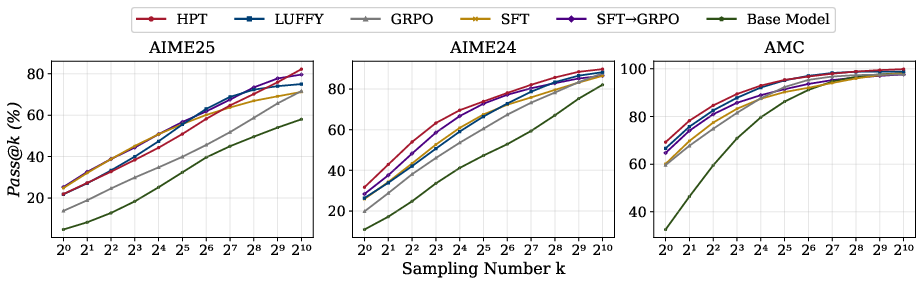
  Figure 2: Pass@k performance of black against baselines on Qwen2.5-Math-7B, demonstrating superior exploration and generalization.

• Analysis of exclusive solves on MATH-500 shows that black acquires substantially more difficult problems than baselines, with minimal catastrophic forgetting.
• Training visualizations reveal that black stabilizes learning and outperforms sequential SFT$\rightarrow$GRPO, especially on harder problems.

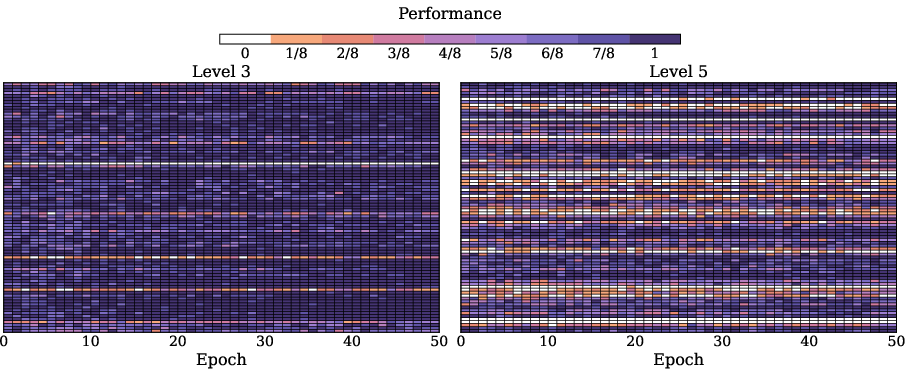
  Figure 3: GRPO training dynamics of SFT$\rightarrow$GRPO on Qwen2.5-Math-1.5B, illustrating per-question sampling accuracy and the limitations of pure RL.

  

  Figure 4: Performance difference (black vs. SFT$\rightarrow$GRPO) on Qwen2.5-Math-1.5B, with red indicating black's advantage.

• Validation performance, entropy, and response length metrics confirm that black maintains higher output diversity and internalizes long-form reasoning patterns from offline data.

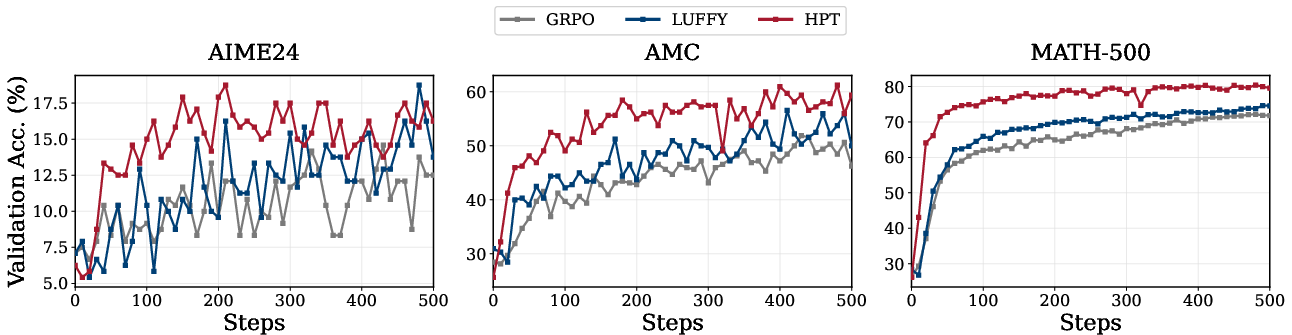
  Figure 5: Validation performance comparisons on Qwen2.5-Math-1.5B across benchmarks, showing stable improvements with black.

  

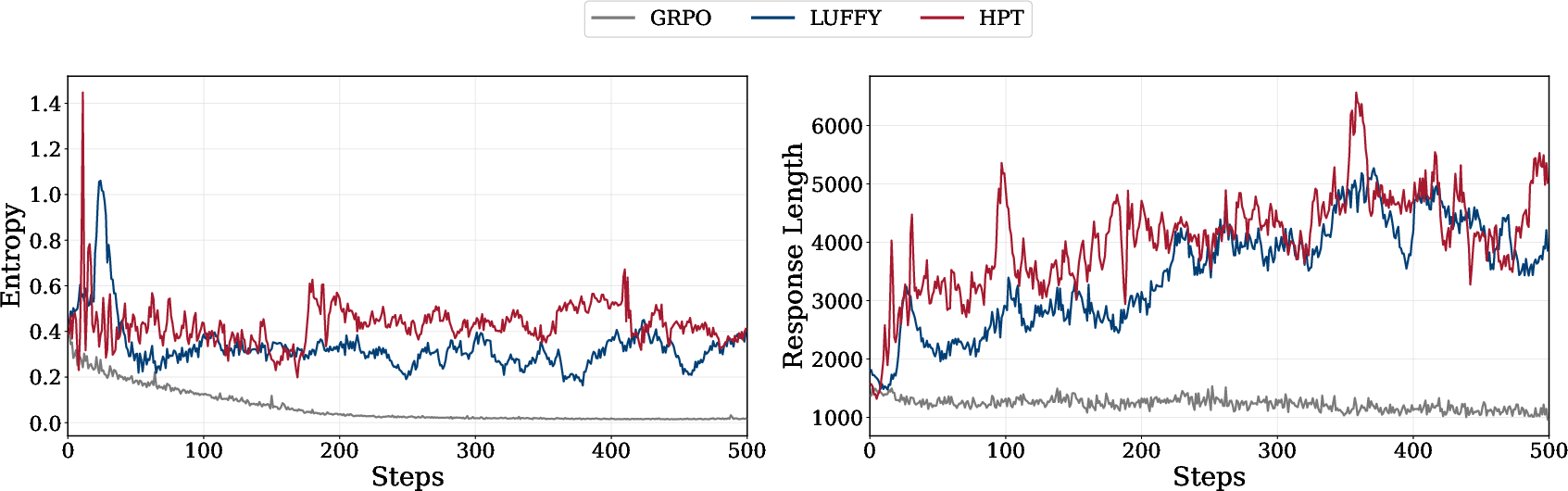
  Figure 6: Training dynamics across methods: (left) entropy measures output diversity; (right) response length tracks reasoning pattern acquisition.

• Ablation studies on gate threshold $\gamma$ show that dynamic adaptation (lower $\gamma$) yields optimal performance, and excessive reliance on SFT degrades results.

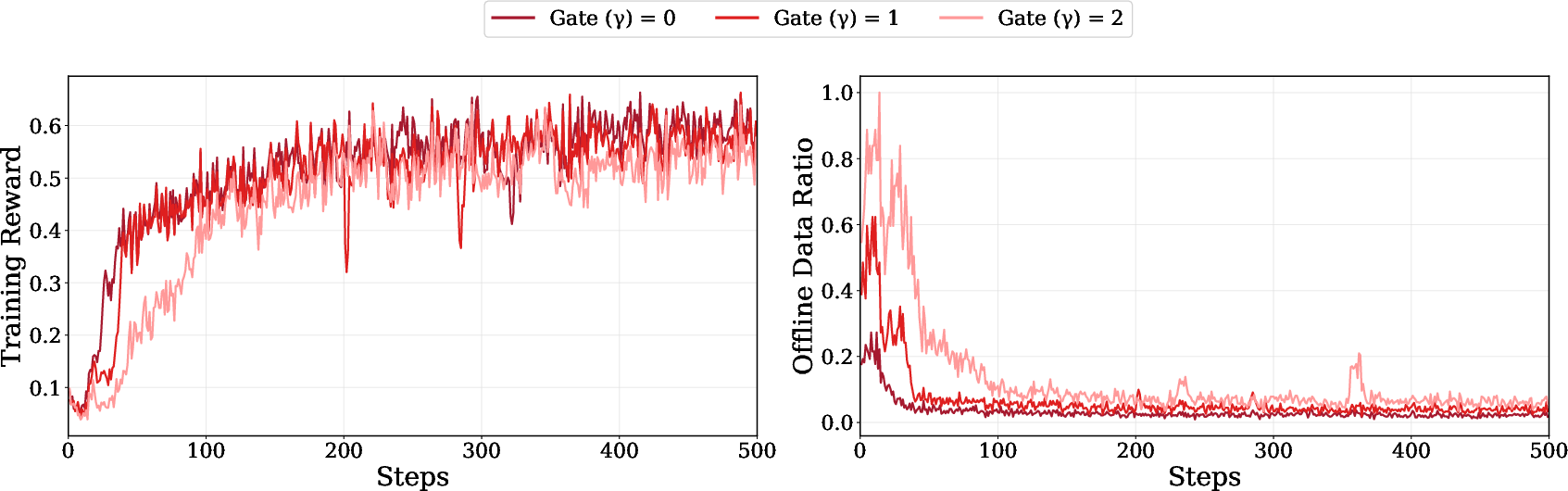
  Figure 7: Training reward and offline data ratio comparisons across gate settings, highlighting the impact of gating on learning dynamics.

Practical and Theoretical Implications

The unified framework provides a principled basis for designing post-training algorithms that flexibly combine SFT and RL signals. The modular decomposition enables systematic analysis and optimization of bias-variance tradeoffs. The empirical results demonstrate that dynamic integration of SFT and RL is superior to static or sequential approaches, both in terms of sample efficiency and generalization.

Practically, the black algorithm can be implemented with minimal overhead, requiring only per-question rollout accuracy and a simple gating mechanism. The approach is robust across model scales and architectures, and is compatible with existing RL and SFT pipelines.

Theoretically, the UPGE formalism suggests that future post-training algorithms should be viewed as instances of a broader class of policy gradient estimators, with component choices tailored to model capability, data distribution, and task complexity. The framework also opens avenues for meta-gradient-based controllers, adaptive advantage estimation, and more granular token-level optimization.

Future Directions

Potential future developments include:

• Extension of UPGE to multi-modal and multi-agent LLMs.
• Automated meta-learning of gating and component selection.
• Integration with preference optimization and reward modeling.
• Exploration of token-level advantage estimation and entropy regularization.
• Application to continual learning and lifelong adaptation in LLMs.

Conclusion

This work establishes a unified theoretical and empirical foundation for LLM post-training, demonstrating that SFT and RL are complementary signals that can be jointly optimized via the Unified Policy Gradient Estimator. The proposed Hybrid Post-Training algorithm (black) leverages dynamic performance feedback to balance exploitation and exploration, achieving strong empirical gains across diverse models and benchmarks. The modular framework and adaptive algorithm provide a robust basis for future research and practical deployment of post-training methods in LLMs.