Randomness with constraints: constructing minimal models for high-dimensional biology (2509.03765v1)

Abstract: Biologists and physicists have a rich tradition of modeling living systems with simple models composed of a few interacting components. Despite the remarkable success of this approach, it remains unclear how to use such finely tuned models to study complex biological systems composed of numerous heterogeneous, interacting components. One possible strategy for taming this biological complexity is to embrace the idea that many biological behaviors we observe are typical'' and can be modeled using random systems that respect biologically-motivated constraints. Here, we review recent works showing how this approach can be used to make close connection with experiments in biological systems ranging from neuroscience to ecology and evolution and beyond. Collectively, these works suggest that therandom-with-constraints'' paradigm represents a promising new modeling strategy for capturing experimentally observed dynamical and statistical features in high-dimensional biological data and provides a powerful minimal modeling philosophy for biology.

• The paper introduces a random-with-constraints model that leverages biologically motivated constraints to capture the dynamics of high-dimensional biological systems.
• The paper applies statistical physics methods like random matrix theory and DMFT to reveal phase transitions and stability in diverse biological networks.
• The paper demonstrates the model's predictive power by quantitatively matching experimental patterns in neuroscience, ecology, and evolutionary studies.

Randomness with Constraints: Minimal Modeling for High-Dimensional Biology

Introduction

The paper "Randomness with constraints: constructing minimal models for high-dimensional biology" (2509.03765) presents a comprehensive perspective on the use of random network ensembles, subject to biologically motivated constraints, as minimal models for complex biological systems. This paradigm is positioned as an alternative to traditional small-circuit mechanistic models, which often fail to scale to the high-dimensionality and heterogeneity observed in modern biological datasets. The authors argue that embracing typicality—modeling biological systems as random networks constrained by broad structural and functional priors—enables quantitative predictions and insights into emergent phenomena across domains such as neuroscience, ecology, evolution, and beyond.

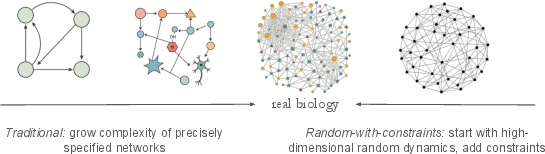
Figure 1: Contrasting traditional bottom-up modeling with the random-with-constraints approach, which starts from high-dimensional random networks and incrementally imposes biologically-informed constraints.

Theoretical Foundations

The random-with-constraints approach draws inspiration from statistical physics, particularly Wigner's random matrix theory in nuclear physics, where ensembles of random matrices subject to symmetry constraints yield universal predictions for spectral statistics. In biology, the analogous strategy is to specify ensembles of random networks, constrained by features such as cell types, interaction symmetries, connectivity statistics, conservation laws, or evolutionary priors, and to analyze their emergent dynamics.

Historically, this methodology has roots in Kauffman's random Boolean networks for gene regulation, Jerne's idiotypic network theory in immunology, May's random community matrices in ecology, Derrida's random energy model in protein folding, and random neural networks in theoretical neuroscience. The common thread is the sacrifice of microscopic specificity in favor of ensemble statistics, leveraging tools such as replica theory, dynamical mean-field theory (DMFT), and random matrix theory to extract generic behaviors—phase transitions, stability criteria, attractor structures—of typical networks under constraints.

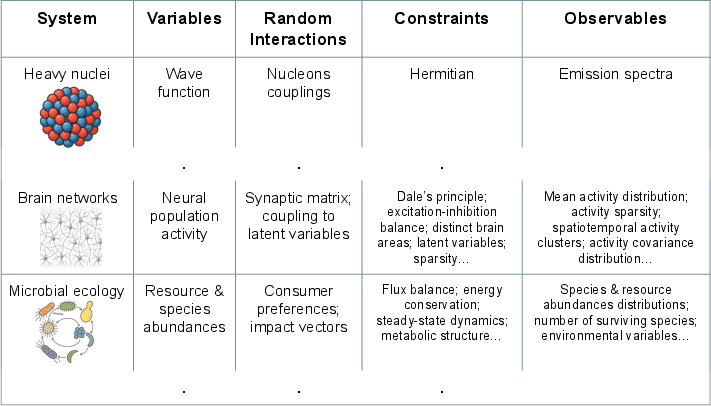
Figure 2: The random-with-constraints paradigm originated in nuclear physics and has been adapted to neuroscience, ecology, and other domains, each requiring distinct variables and constraint sets.

Empirical Validation Across Biological Domains

Neuroscience

Recent advances in large-scale neural recording and connectomics have rendered fine-tuned circuit models increasingly impractical. Random network models, especially those incorporating excitation-inhibition (E-I) balance and Dale's principle, have demonstrated quantitative agreement with experimental covariance spectra, single-cell selectivity, and population correlation patterns in cortical and hippocampal recordings. Notably, random balanced networks reproduce nonlinear population responses and low-dimensional correlated activity observed in mouse cortex and zebrafish whole-brain imaging. Constraints such as bipartite structure, geometric embedding, and sparsity have been shown to explain critical scaling, invariance to subsampling, and place-cell statistics with high precision.

Reservoir computing regimes and structured random connectivity have been used to model information routing and dimensionality reduction in primate prefrontal cortex and macaque V1. Sparse random connectivity models accurately predict synaptic statistics in cerebellar and Drosophila circuits. These results collectively support the claim that random-with-constraints models, rather than hand-crafted minimal circuits, are increasingly effective as minimal models for high-dimensional neural data.

Ecology and Evolution

The proliferation of high-throughput sequencing has enabled quantitative measurement of species abundances in microbial ecosystems, revealing large-scale patterns such as species abundance distributions and modularity. High-dimensional random consumer-resource models, augmented with metabolic constraints, have successfully explained these patterns and predicted phase transitions between niche-like and neutral regimes, which have been experimentally validated. Random-with-constraints models have also elucidated the role of metabolic cross-feeding and macroecological patterns across diverse environments.

In evolutionary biology, random fitness landscapes have reproduced global patterns of epistasis and made quantitative predictions about the relationship between global and microscopic epistatic effects, verified by experimental reanalysis. Eco-evolutionary dynamics modeled by random systems have explained the coexistence of closely related strains, a phenomenon not captured by low-dimensional population genetic models.

Other Domains

Random network models have found utility in systems biology (gene regulatory networks with random weights), soft matter biophysics (random-fiber models for tissue elasticity), and immunology (random bipartite antigen-receptor models). These models have achieved quantitative fits to experimental data, such as stress-strain curves in healthy and fibrotic tissues, and have predicted immune system organization and autoimmune responses. The success of these models in diverse fields underscores the generality of the random-with-constraints paradigm.

Implications and Open Questions

The empirical success of random-with-constraints models raises several theoretical and practical questions. First, the existence of universality classes in biological systems—analogous to those in statistical physics—could explain why certain ensembles reproduce core observables. Second, developing predictive criteria for selecting appropriate constraint sets is essential for transforming random-ensemble modeling from an empirical art to a systematic science.

Three hypotheses are proposed for the efficacy of these models:

1. Environmental Alignment: Biological systems may operate in environments whose statistics are well captured by random-feature models, leading to an alignment between environmental structure and emergent dynamics.
2. Evolutionary Flexibility: Evolution may favor solutions that satisfy functional constraints without fine-tuning all interactions, analogous to the lottery ticket hypothesis in machine learning.
3. Dominance of Non-Specific Interactions: In high-dimensional systems, weak non-specific interactions may dominate large-scale patterns, rendering structured and random models indistinguishable at the macroscopic level.

These considerations suggest that randomness with constraints is not merely a modeling convenience but may reflect fundamental principles of biological organization and evolution.

Future Directions

The authors advocate for systematic cross-domain comparisons of random ensemble predictions with experimental data, aiming to refine constraint sets and improve model accuracy. Iterative analysis of model errors could inform the formulation of more biologically relevant constraints. The development of software packages for simulating constrained random networks will facilitate rapid hypothesis testing and model validation.

Further research should focus on formalizing universality principles, automating constraint selection, and exploring the interplay between environmental statistics, evolutionary dynamics, and emergent biological function. The random-with-constraints paradigm is poised to become a central modeling philosophy in quantitative biology, balancing parsimony, realism, and predictive power.

Conclusion

The random-with-constraints approach offers a minimal yet quantitatively robust framework for modeling high-dimensional biological systems. By focusing on ensemble statistics subject to biologically motivated constraints, this paradigm bridges the gap between tractable mechanistic models and the complexity of real biological networks. Its success across neuroscience, ecology, evolution, and other domains suggests that randomness, when appropriately constrained, captures the essential features of living systems. Future work should aim to formalize the principles underlying this success and extend the paradigm to new areas of biological research.