Matroid bingo

Abstract: We investigate some natural probability distributions associated with the game of matroid bingo.

• The paper demonstrates that valid matroid bingo cards are exactly the circuits of a matroid, establishing a novel link between combinatorial game theory and matroid structure.
• It derives both inclusion-exclusion and timed formulas for winning probabilities, revealing properties like log-concavity and providing sharp bounds based on matroid parameters.
• The study uncovers rare monotonicity violations and identifies equitable matroids, prompting deeper investigation into their combinatorial and probabilistic implications.

Matroid Bingo: Probability, Monotonicity, and Equitability in Matroid Circuit Games

Introduction and Matroid Bingo Game Definition

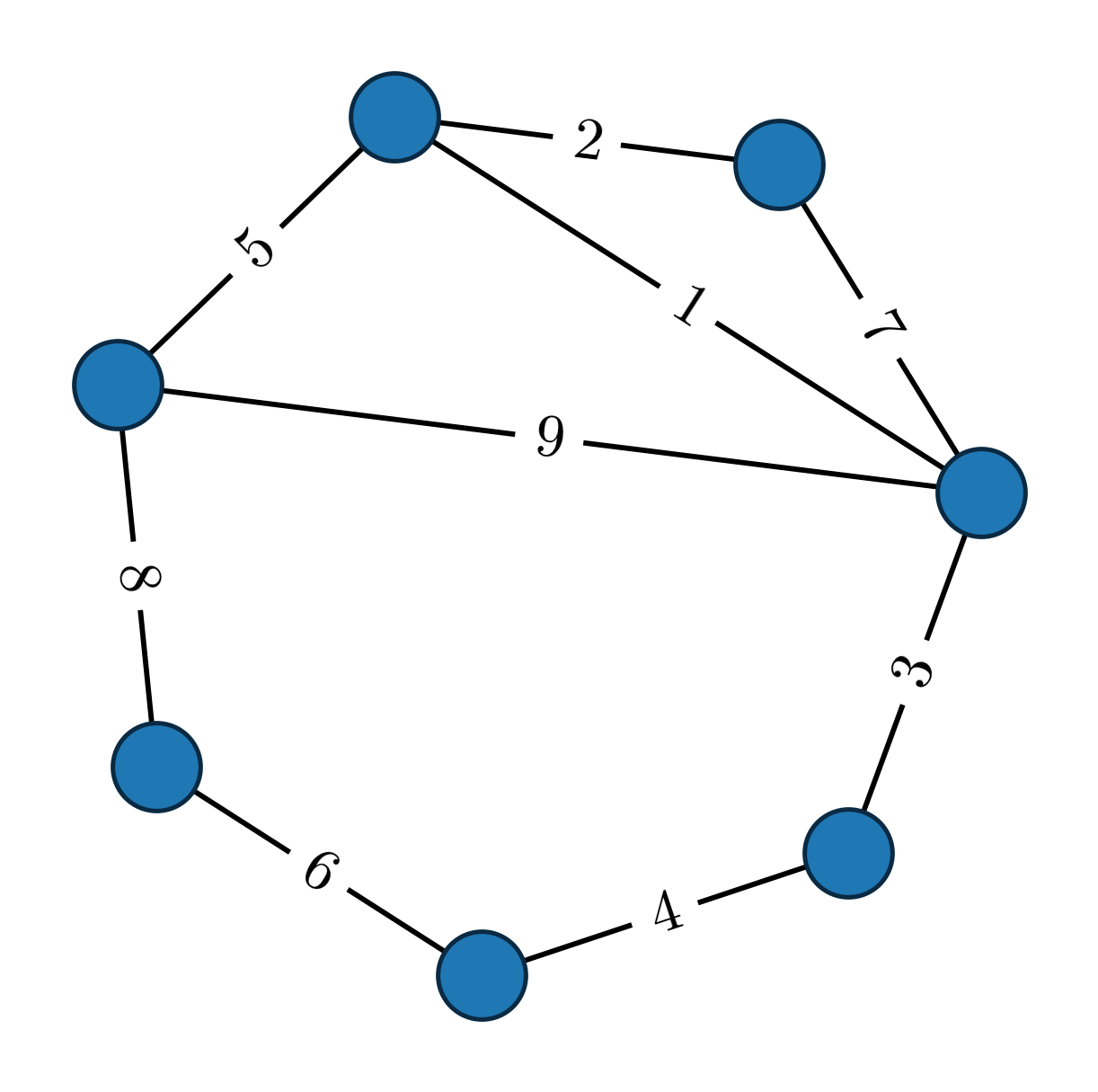
The paper introduces "matroid bingo," a probabilistic game that encodes the circuit axiom system of matroids. Each player receives a card listing a subset of $\{1,\ldots,n\}$, and numbers are drawn randomly until a player completes their card. The design rules for valid cards (no empty cards, no subset containment, and no ties) are shown to be equivalent to the matroid circuit axioms (C1)-(C3). This correspondence is formalized, establishing that the set of valid bingo cards is precisely the set of circuits of a matroid.

Figure 1: A valid set of matroid bingo cards, each corresponding to a circuit of a matroid.

The paper also demonstrates that not all set systems yield valid bingo games, as ties can occur if the circuit elimination axiom is violated.

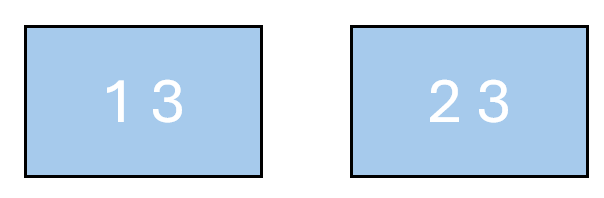
Figure 2: A set of cards for which a tie is possible, violating the matroid circuit axioms.

Monotonicity and Winning Probabilities

A central question is the probability that a given card (circuit) wins, denoted $\beta_C$. The authors derive two formulas for $\beta_C$:

1. Inclusion-Exclusion Formula:

$$\beta_C = \sum_{k=0}^{|\mathcal{C}|-1} (-1)^k \sum_{S \subseteq \mathcal{C} \setminus \{C\}, |S|=k} \frac{|C|}{|(\cup_{C' \in S} C') \cup C|}$$

2. Timed Winning Probability Formula:

$$\beta_C = \sum_{t=|C|}^{r(\mathcal{M})+1} \beta_C(t), \quad \beta_C(t) = \frac{|C|}{n} \cdot |\mathcal{I}_{C, t-|C|}| \cdot \binom{n-1}{t-1}^{-1}$$

where $\mathcal{I}_{C, k}$ is the set of $k$-element subsets of $E \setminus C$ such that $C$ is the unique circuit in $S \cup C$.

The second formula is shown to be more tractable for both theoretical and computational analysis. The connection to the Tutte polynomial is established, allowing enumeration of independent sets via $[x^{r(/C)-k}] T_{/C}(x+1,1)$.

Monotonicity Violations and Their Structure

The paper investigates the phenomenon of monotonicity violations: cases where a larger circuit (card with more numbers) has a higher winning probability than a smaller one. While intuition suggests shorter cards should be favored, the authors provide explicit counterexamples, including both disconnected and connected matroids.

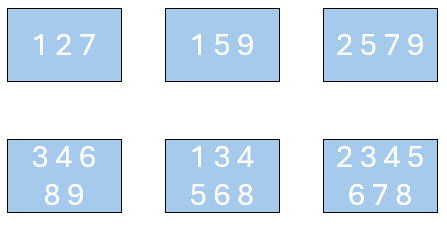
Figure 3: A set of bingo game cards corresponding to a connected matroid with a monotonicity violation.

Numerical analysis reveals that monotonicity violations are rare: only 11 out of 385,360 matroids with up to 9 elements exhibit this behavior. The authors conjecture, based on the paving matroid conjecture and computational evidence, that monotonicity violations are asymptotically negligible.

Log-Concavity and Unimodality of Timed Winning Probabilities

A significant theoretical result is the proof that the sequence of timed winning probabilities $\beta_C(1), \beta_C(2), \ldots, \beta_C(n)$ is log-concave for every circuit $C$ in any matroid. This is established by leveraging the strong version of Mason's conjecture, recently proved via combinatorial Hodge theory, which asserts ultra log-concavity of independent set counts in matroids.

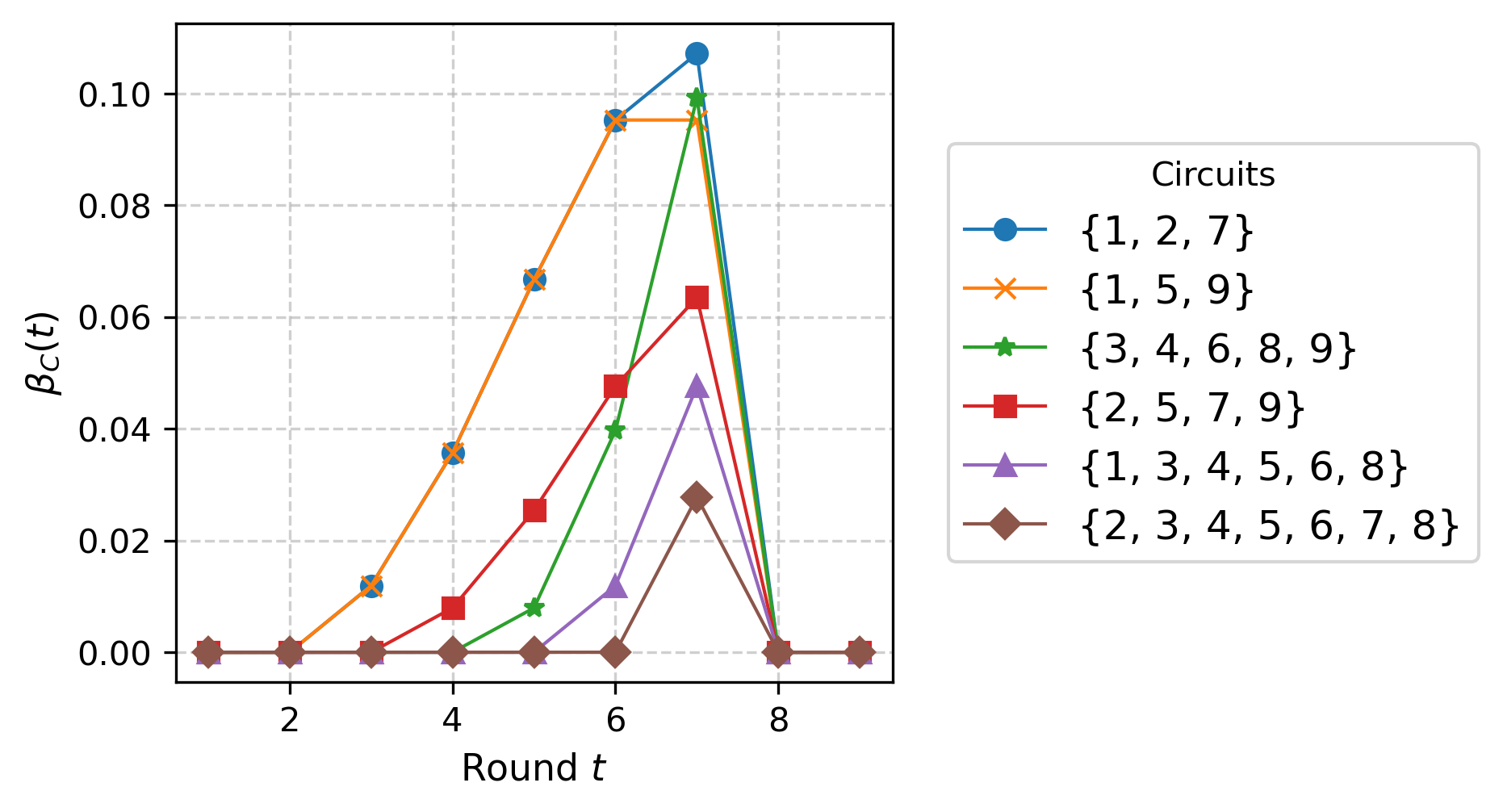
Figure 4: Timed winning probabilities for the matroid in Figure 3, illustrating log-concavity and unimodality.

This log-concavity implies unimodality, confirming that the probability of winning as a function of the round number increases to a peak and then decreases.

Bounds on Winning Probabilities

The authors derive sharp upper and lower bounds for $\beta_C$ in terms of the matroid rank $r$, ground set size $n$, and circuit size $|C|$:

• Upper Bound:

$$\beta_C \leq \frac{\binom{r+1}{|C|}}{\binom{n}{|C|}}$$

• Lower Bound:

$\beta_C \geq \binom{n-d}{|C|}^{-1}$

where $d = r+1 - |C|$.

These bounds are shown to be sharp for certain matroid constructions. Notably, all circuits of maximal size $r+1$ have equal winning probability, and monotonicity always holds for these cases.

Thresholds for Monotonicity and Asymptotic Behavior

The paper proves that for fixed rank $r$, there exists a threshold $N(r)$ such that monotonicity holds for all matroids of rank $r$ on $n \geq N(r)$ elements. The proof uses asymptotic analysis of the derived bounds, showing that the upper bound for larger circuits becomes strictly less than the lower bound for smaller circuits as $n$ grows.

Equitable Matroids

A matroid is called equitable if all circuits have equal winning probability. The authors show that:

• Uniform matroids and duals of projective geometries over finite fields are equitable.
• Equitability is guaranteed if the automorphism group acts transitively on circuits, but there exist equitable matroids without transitive automorphism groups.

  Figure 5: A graphic representation of the matroid depicted in Figure 3, illustrating the connection between graphic matroids and monotonicity violations.

Classifying all equitable matroids remains an open problem.

Implications and Future Directions

The results have both combinatorial and probabilistic implications:

• The connection between matroid theory and probability via the bingo game provides new intuition for matroid cryptomorphisms.
• The log-concavity result links matroid theory to combinatorial Hodge theory and unimodality phenomena.
• The rarity of monotonicity violations and the equitability results suggest that most matroids behave "fairly" in the context of the bingo game.

Potential future directions include:

• Classification of equitable matroids beyond uniform and projective geometry duals.
• Investigation of monotonicity violations in larger matroids and their structural causes.
• Extension of the probabilistic analysis to other matroid cryptomorphisms and related combinatorial games.

Conclusion

This paper establishes a deep connection between matroid circuit theory and probabilistic games, providing explicit formulas, bounds, and structural results for winning probabilities in matroid bingo. The analysis of monotonicity, log-concavity, and equitability enriches both the combinatorial and probabilistic understanding of matroids, and opens avenues for further research in matroid theory, combinatorial probability, and algebraic combinatorics.