GradES: Significantly Faster Training in Transformers with Gradient-Based Early Stopping (2509.01842v1)

Abstract: Early stopping monitors global validation loss and halts all parameter updates simultaneously, which is computationally costly for large transformers due to the extended time required for validation inference. We propose GradES, a novel gradient-based early stopping approach that operates within transformer components (attention projections and Feed-Forward layer matrices). We found that different components converge at varying rates during fine-tuning. GradES tracks the magnitude of gradients in backpropagation for these matrices during training. When a projection matrix's gradients fall below a convergence threshold $\tau$, we exclude that projection matrix from further updates individually, eliminating costly validation passes while allowing slow converging matrices to continue learning. By strategically freezing parameters when their gradients converge, GradES speeds up training time by 1.57--7.22$\times$ while simultaneously enhancing generalization through early prevention of overfitting, resulting in 1.2% higher average accuracy.

• The paper introduces a gradient-based early stopping mechanism that freezes individual transformer matrices when their gradients fall below a set threshold.
• It demonstrates significant efficiency gains with training speedups up to 7.22×, FLOPs reductions of 29–45%, and accuracy improvements up to 1.2%.
• GradES dynamically adapts to heterogeneous convergence in transformer components and integrates seamlessly with full-parameter fine-tuning and PEFT methods like LoRA.

Gradient-Based Early Stopping for Efficient Transformer Fine-Tuning: The GradES Approach

Introduction

The GradES algorithm introduces a matrix-level, gradient-based early stopping mechanism for transformer architectures, addressing the inefficiencies of conventional validation-based early stopping. By leveraging the heterogeneous convergence rates of transformer components—specifically attention projections and MLP matrices—GradES adaptively freezes individual weight matrices when their gradient magnitudes fall below a threshold, thereby reducing unnecessary parameter updates and computational overhead. This approach is shown to yield substantial improvements in both training efficiency and generalization performance across a range of LLMs and parameter-efficient fine-tuning (PEFT) methods.

Motivation: Heterogeneous Convergence in Transformer Components

Empirical analysis reveals that different transformer components exhibit distinct convergence patterns during fine-tuning. Attention projection matrices ($\mathbf{W}_q$, $\mathbf{W}_k$, $\mathbf{W}_v$, $\mathbf{W}_o$) typically stabilize much earlier than MLP matrices ($\mathbf{W}_{\text{gate}}$, $\mathbf{W}_{\text{up}}$, $\mathbf{W}_{\text{down}}$), which maintain higher gradient magnitudes and require more training steps to converge.

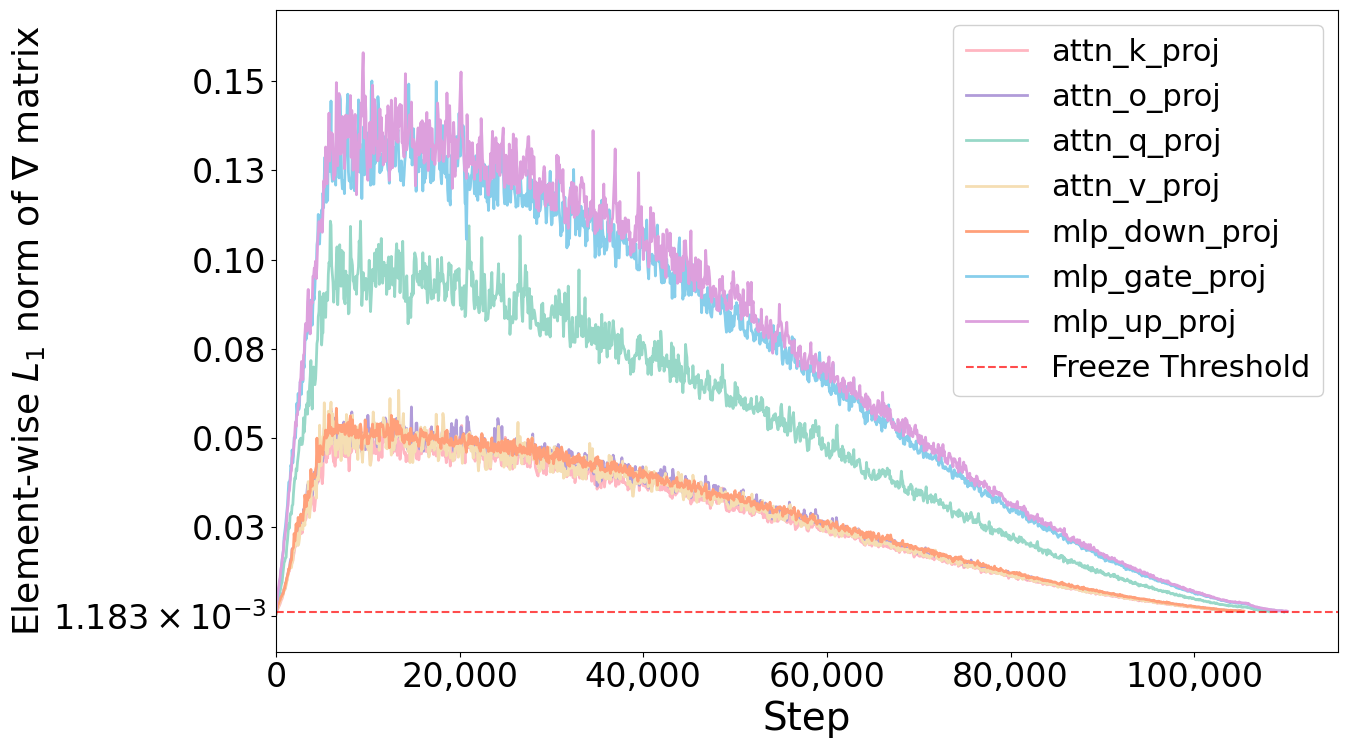
Figure 1: Element-wise $L_1$ norms for the gradient matrix of transformer components during fine-tuning with LoRA on Qwen3-0.6B. MLP projections exhibit 2–3$\times$ higher gradient magnitudes than attention projections throughout training, with $\mathbf{W}_{\text{up}}$ and $\mathbf{W}_{\text{down}}$ maintaining the largest gradients. The red dotted line indicates the convergence threshold $\tau$.

This disparity motivates a component-specific approach to early stopping, as uniform training strategies fail to exploit the efficiency gains available from freezing fast-converging components.

GradES Algorithm: Matrix-Level Gradient Monitoring and Freezing

GradES operates by tracking the element-wise $L_1$ norm of gradients for each weight matrix in every transformer layer. After a configurable grace period (typically 55% of total training steps), the algorithm monitors gradient magnitudes and freezes matrices whose gradients fall below a threshold $\tau$. Frozen matrices cease to receive parameter updates but continue to participate in gradient flow, preserving backpropagation integrity.

The algorithm is compatible with both full-parameter fine-tuning and PEFT methods such as LoRA, with gradient monitoring adapted to the low-rank parameter space in the latter case. The $L_1$ norm is selected for its computational efficiency and its property as a universal upper bound for other matrix norms, ensuring robust convergence detection.

Empirical Results: Accuracy and Efficiency

GradES is evaluated on five transformer models (Qwen3-14B, Phi4-14B, Llama-3.1-8B, Mistral-7B, Qwen3-0.6B) and eight commonsense reasoning benchmarks. Across all configurations, GradES consistently matches or exceeds the accuracy of baseline early stopping and standard fine-tuning methods, with up to 1.2% higher average accuracy.

In terms of efficiency, GradES achieves training speedups of 1.57–7.22$\times$ and FLOPs reductions of 29–45% for full-parameter fine-tuning. When combined with LoRA, GradES delivers the fastest training times, completing fine-tuning in as little as 14% of the baseline time for Qwen3-0.6B, with no loss in accuracy.

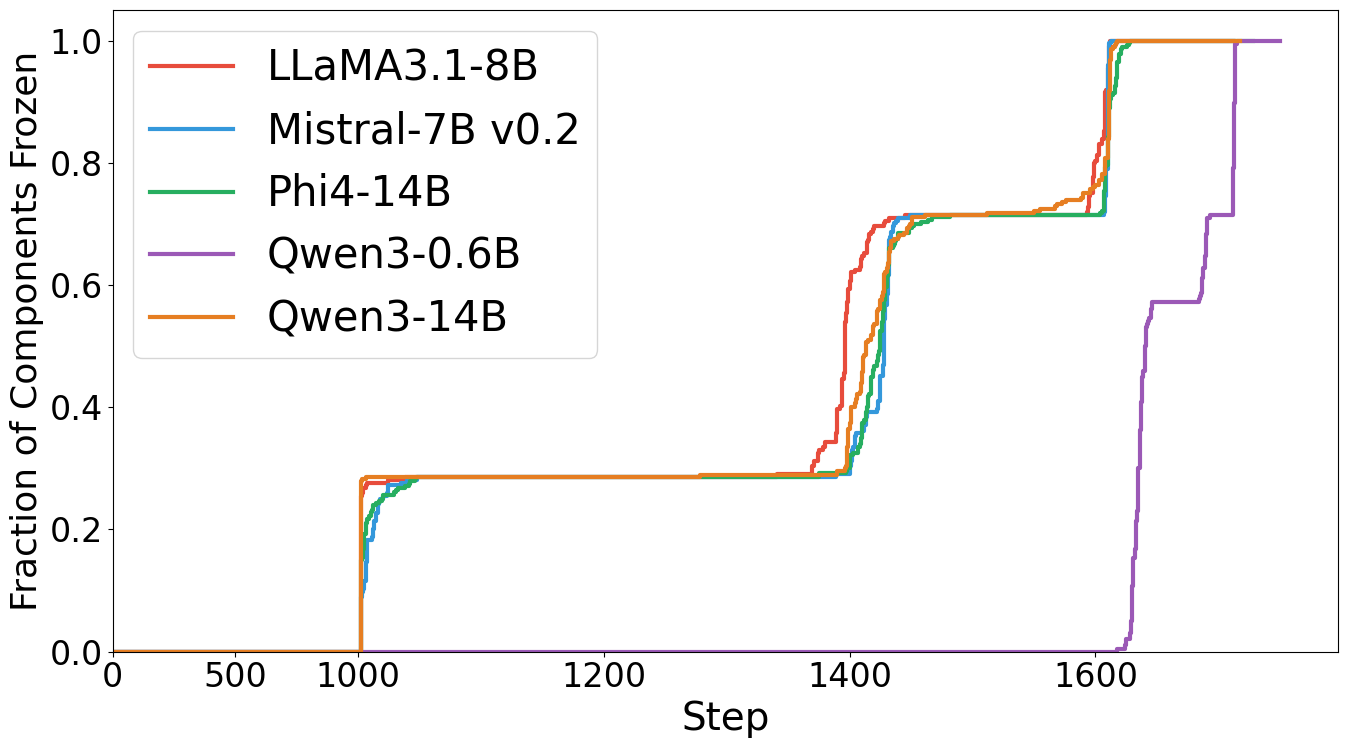
Figure 2: Cumulative frozen components during training across model scales. Fraction of weight matrices frozen over time for five different LLMs.

The progression of frozen components demonstrates rapid convergence in larger models, with most matrices frozen by step 1400, while smaller models exhibit delayed convergence.

Analysis: Attention vs. MLP Dynamics

A key finding is the persistent gap in gradient magnitudes between attention and MLP matrices. MLP components require more training steps to converge, indicating inefficiency in uniform update schedules.

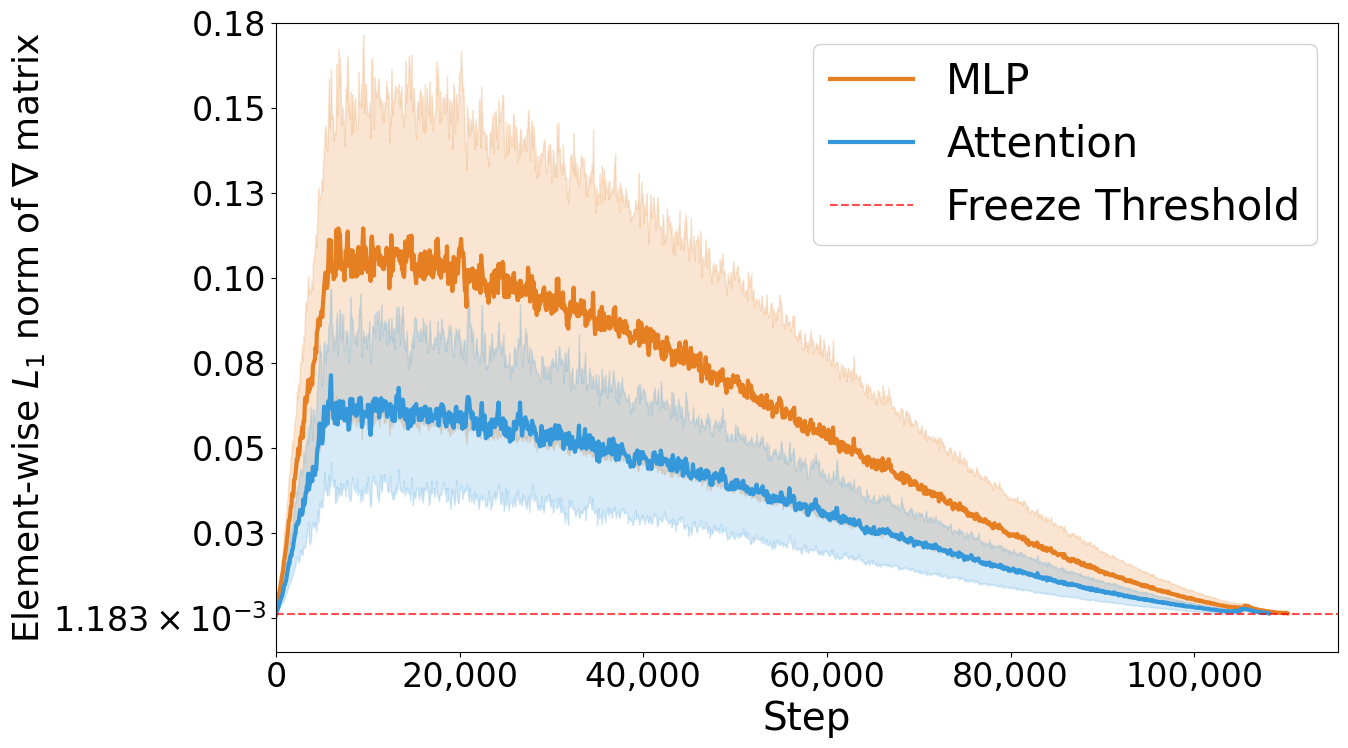
Figure 3: Gradient norm evolution during Qwen-0.6B fine-tuning. Element-wise L1 norms of weight gradients averaged across layers for MLP matrices (orange) and attention projections (blue). MLP matrices consistently exhibit larger gradient magnitudes throughout training, indicating slower convergence and motivating targeted computational allocation.

This observation supports the GradES strategy of allocating computational resources in proportion to gradient magnitudes, accelerating convergence for slower-learning components.

Integration with PEFT and Comparison to Classic Early Stopping

GradES integrates seamlessly with LoRA and other PEFT methods, compounding efficiency gains from both parameter reduction and adaptive freezing. In contrast, classic early stopping incurs significant validation overhead and applies a global convergence criterion, which is suboptimal for transformer architectures with heterogeneous component dynamics.

GradES eliminates the need for costly validation passes by reusing gradient information from backpropagation, yielding substantial computational savings and more precise convergence control.

Limitations and Future Directions

GradES introduces a minor computational overhead (~3%) for gradient monitoring, which is negligible relative to the overall speedup. The convergence threshold $\tau$ requires manual tuning, and the current implementation lacks patience mechanisms, potentially leading to premature freezing. Applicability to non-transformer architectures remains to be explored.

Future work should focus on automatic threshold selection, dynamic freezing/unfreezing, integration with additional efficiency techniques (e.g., mixed precision, gradient checkpointing), and extension to pretraining and other neural architectures.

Conclusion

GradES provides a principled, efficient approach to transformer fine-tuning by exploiting the heterogeneous convergence rates of model components. By monitoring gradient magnitudes and adaptively freezing converged matrices, GradES achieves substantial reductions in training time and computational cost while maintaining or improving model accuracy. The method is generalizable across model scales and architectures, and its integration with PEFT methods such as LoRA yields multiplicative efficiency gains. As LLMs continue to scale, gradient-based optimization strategies like GradES will be essential for resource-efficient model development and deployment.