Data Retrieval with Importance Weights for Few-Shot Imitation Learning (2509.01657v1)

Abstract: While large-scale robot datasets have propelled recent progress in imitation learning, learning from smaller task specific datasets remains critical for deployment in new environments and unseen tasks. One such approach to few-shot imitation learning is retrieval-based imitation learning, which extracts relevant samples from large, widely available prior datasets to augment a limited demonstration dataset. To determine the relevant data from prior datasets, retrieval-based approaches most commonly calculate a prior data point's minimum distance to a point in the target dataset in latent space. While retrieval-based methods have shown success using this metric for data selection, we demonstrate its equivalence to the limit of a Gaussian kernel density (KDE) estimate of the target data distribution. This reveals two shortcomings of the retrieval rule used in prior work. First, it relies on high-variance nearest neighbor estimates that are susceptible to noise. Second, it does not account for the distribution of prior data when retrieving data. To address these issues, we introduce Importance Weighted Retrieval (IWR), which estimates importance weights, or the ratio between the target and prior data distributions for retrieval, using Gaussian KDEs. By considering the probability ratio, IWR seeks to mitigate the bias of previous selection rules, and by using reasonable modeling parameters, IWR effectively smooths estimates using all data points. Across both simulation environments and real-world evaluations on the Bridge dataset we find that our method, IWR, consistently improves performance of existing retrieval-based methods, despite only requiring minor modifications.

• The paper introduces IWR to reformulate data retrieval as an importance sampling problem, reducing bias and variance compared to nearest-neighbor methods.
• It employs Gaussian KDE to estimate density ratios between target and prior datasets, enabling principled selection of samples for effective policy co-training.
• Experimental evaluations demonstrate significant improvements in success rates across simulated and real-world robotic tasks over established baselines.

Importance Weighted Retrieval for Few-Shot Imitation Learning

Introduction

The paper "Data Retrieval with Importance Weights for Few-Shot Imitation Learning" (2509.01657) addresses the challenge of learning robust robotic policies from limited task-specific demonstrations by leveraging large-scale prior datasets. The central contribution is the introduction of Importance Weighted Retrieval (IWR), a method that reframes data retrieval for imitation learning as an importance sampling problem, thereby correcting the bias and high variance inherent in previous nearest-neighbor-based retrieval approaches. IWR utilizes Gaussian kernel density estimation (KDE) to estimate the ratio between the target and prior data distributions, enabling more principled and effective selection of relevant prior data for policy co-training.

Background and Motivation

Imitation learning (IL) in robotics typically requires extensive expert demonstrations for each new task, which is costly and limits scalability. Retrieval-based methods attempt to mitigate this by augmenting small, high-quality target datasets with relevant samples from large, diverse prior datasets. Existing approaches predominantly rely on nearest-neighbor (L2) distance in a learned latent space to select prior data points similar to the target demonstrations. However, this heuristic is equivalent to a limiting case of a Gaussian KDE and suffers from two key issues:

1. High Variance: Nearest-neighbor estimates are sensitive to noise and outliers.
2. Distributional Bias: These methods ignore the distribution of the prior data, leading to a mismatch between the retrieved and target distributions.

IWR addresses both issues by explicitly modeling the densities of both the target and prior datasets and retrieving data according to their importance weights.

Methodology

Probabilistic Formulation of Retrieval

The objective is to learn a policy $\pi_\theta(a|s)$ that maximizes expected log-likelihood under the target distribution $t$:

$$\max_\theta \quad \mathbb{E}_{(s,a) \sim t}[\log \pi_\theta(a|s)]$$

Retrieval-based methods augment the target dataset $D_t$ with a subset $D_r$ of prior data $D_p$, leading to a weighted behavior cloning objective:

$$\max_\theta \quad \alpha \frac{1}{|D_t|} \sum_{(s,a) \in D_t} \log \pi_\theta(a|s) + (1-\alpha) \frac{1}{|D_r|} \sum_{(s,a) \in D_r} \log \pi_\theta(a|s)$$

The goal is to select $D_r$ such that its distribution matches $t$ as closely as possible.

Importance Weighted Retrieval (IWR)

IWR reframes retrieval as an importance sampling problem. The key steps are:

1. Representation Learning: Learn a low-dimensional embedding $z = f_\phi(s, a)$ using a VAE or similar model.
2. Density Estimation: Fit Gaussian KDEs to the embeddings of the target ($t^{\text{KDE}}$) and prior ($\text{prior}^{\text{KDE}}$) datasets.
3. Importance Weight Computation: For each candidate prior data point, compute the importance weight as the ratio $t^{\text{KDE}}(z) / \text{prior}^{\text{KDE}}(z)$.
4. Data Selection: Retrieve prior data points with the highest importance weights, using a threshold $\eta$ determined empirically.
5. Policy Co-Training: Train the policy on the union of the target and retrieved data.

This approach smooths the density estimates, reduces variance, and corrects for the bias introduced by the prior data distribution.

Figure 1: IWR consists of three main steps: (A) Learning a latent space to encode state-action pairs, (B) Estimating a probability distribution over the target and prior data, and using importance weights for data retrieval, and (C) Co-training on the target data and retrieved prior data.

Theoretical Justification

The nearest-neighbor L2 retrieval rule is shown to be a limiting case of KDE-based density estimation as the bandwidth approaches zero. By using KDEs with well-chosen bandwidths (e.g., Scott's rule), IWR provides a lower-variance, more robust estimate of the target density. The importance weighting ensures that the expectation under the retrieved data matches that of the target distribution, aligning the retrieval process with the theoretical objective of imitation learning.

Experimental Evaluation

Benchmarks and Baselines

IWR is evaluated on both simulated (Robomimic Square, LIBERO-10) and real-world (Bridge V2) robotic manipulation tasks. Baselines include:

• Behavior Cloning (BC): Trained only on target data.
• Behavior Retrieval (BR): VAE-based L2 retrieval.
• Flow Retrieval (FR): Optical flow-based VAE retrieval.
• SAILOR (SR): Skill-based latent retrieval.
• STRAP: Trajectory-based retrieval using dynamic time warping.

Performance Results

IWR consistently outperforms all baselines across simulated and real tasks. Notably:

• On LIBERO, IWR improves average success rates by 5.8% over SAILOR, 4.4% over Flow Retrieval, and 5.8% over Behavior Retrieval.
• On Bridge V2 real-world tasks, IWR increases success rates by 30% on average compared to BR.
• For long-horizon tasks (e.g., Eggplant), IWR achieves 100% partial success, compared to 50% for the best baseline.

Retrieval Quality Analysis

IWR retrieves a higher proportion of directly relevant and temporally appropriate samples compared to BR, which often retrieves irrelevant or initial-phase samples due to distributional bias.

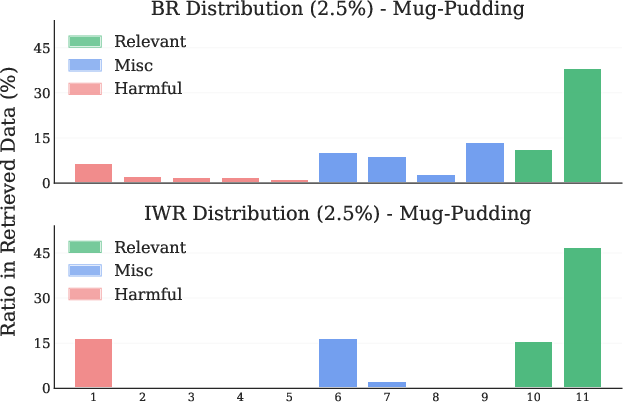
Figure 2: Difference in retrieval distributions between BR and IWR for the Mug-Pudding task in terms of both tasks (left) and timesteps (right).

Figure 3: Mug-Microwave LIBERO Task. (Left) Retrieval distribution across tasks. (Right) Retrieval distribution across timesteps.

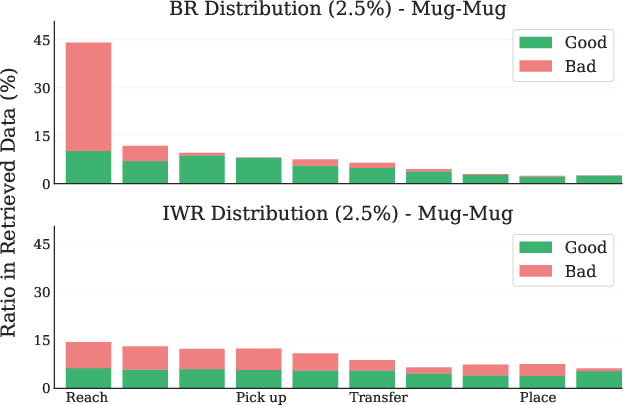
Figure 4: Mug-Mug LIBERO Task. (Left) Retrieval distribution across tasks. (Right) Retrieval distribution across timesteps.

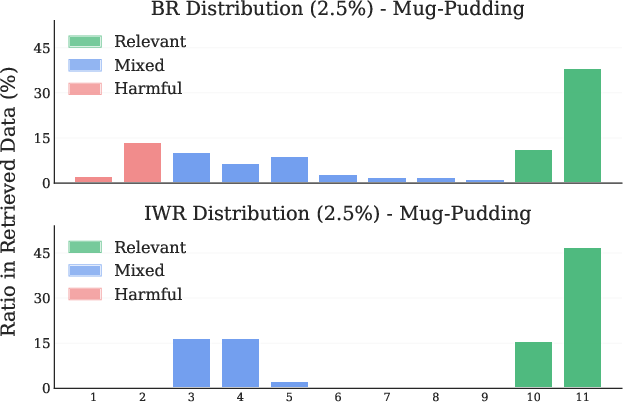
Figure 5: Mug-Pudding LIBERO Task. (Left) Retrieval distribution across tasks. (Right) Retrieval distribution across timesteps.

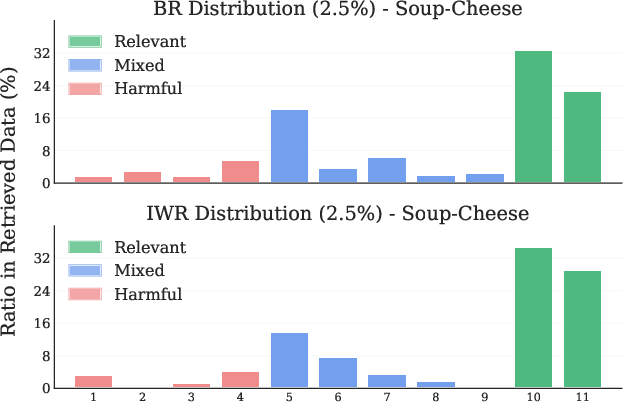
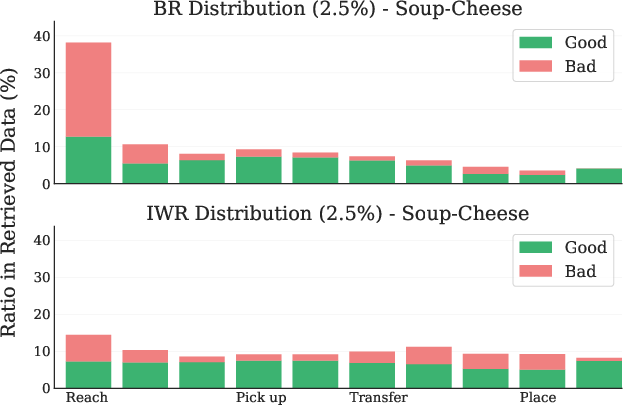
Figure 6: Soup-Cheese LIBERO Task. (Left) Retrieval distribution across tasks. (Right) Retrieval distribution across timesteps.

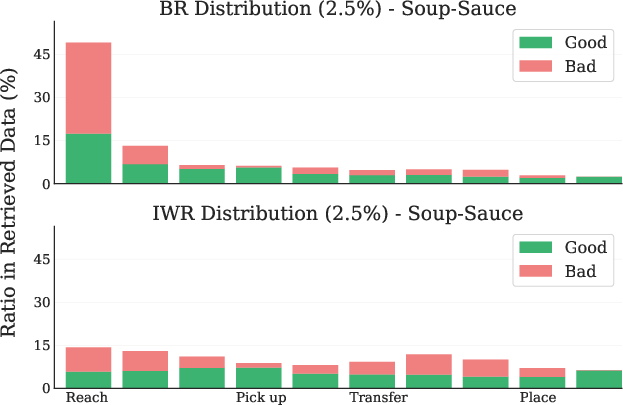
Figure 7: Soup-Sauce LIBERO Task. (Left) Retrieval distribution across tasks. (Right) Retrieval distribution across timesteps.

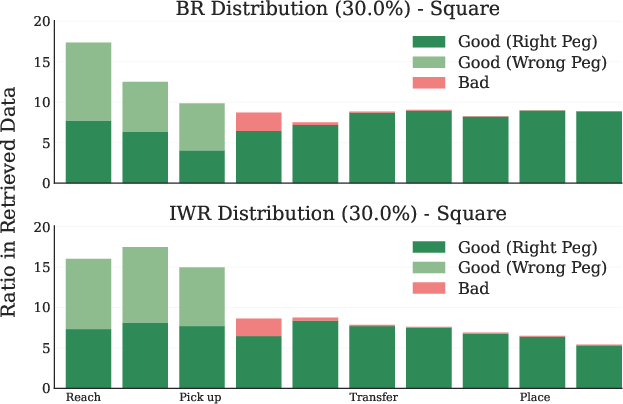
Figure 8: Retrieval distribution across timesteps for Robomimic Square Task.

Ablations and Analysis

• Importance Weight Normalization: Removing the denominator (prior density) in the importance weight degrades performance, confirming the necessity of proper importance weighting.
• Bandwidth Sensitivity: IWR is robust to moderate changes in KDE bandwidth, but overly narrow bandwidths increase variance.
• Retrieval Threshold: Performance is sensitive to the proportion of prior data retrieved; excessive retrieval introduces harmful samples.
• Latent Space Choice: IWR is effective with VAE-based latent spaces but fails with non-smooth representations (e.g., BYOL), highlighting the importance of latent space smoothness for KDE-based retrieval.

Practical Implications and Limitations

IWR is straightforward to implement and can be integrated into existing retrieval-based imitation learning pipelines with minimal modification. The method is agnostic to the specific representation learning approach, provided the latent space is low-dimensional and smooth. However, KDE-based density estimation becomes computationally intractable in high-dimensional spaces, limiting the scalability of IWR to higher-dimensional latent representations. Additionally, the method's efficacy is contingent on the quality of the learned latent space; non-smooth or poorly structured embeddings undermine the benefits of KDE-based retrieval.

Future Directions

Potential avenues for future research include:

• Developing scalable density ratio estimation techniques for high-dimensional latent spaces (e.g., using deep generative models or classifier-based density ratio estimation).
• Investigating the properties of effective latent spaces for retrieval and designing representation learning objectives tailored for importance-weighted retrieval.
• Extending IWR to more complex, dexterous, or multi-stage robotic tasks beyond pick-and-place.
• Exploring adaptive or learned retrieval thresholds to further automate the data selection process.

Conclusion

Importance Weighted Retrieval provides a principled, theoretically grounded, and empirically validated approach to data retrieval for few-shot imitation learning. By leveraging importance sampling and KDE-based density estimation, IWR corrects the bias and variance issues of previous retrieval heuristics, resulting in more robust and performant policies across a range of simulated and real-world robotic tasks. The method's simplicity and compatibility with existing pipelines suggest it should become standard practice in retrieval-based imitation learning, though further work is needed to address scalability and representation learning challenges.