Reasoning Vectors: Transferring Chain-of-Thought Capabilities via Task Arithmetic (2509.01363v1)

Abstract: LLMs often require costly optimization, such as reinforcement learning, to master complex reasoning tasks. This work demonstrates that reasoning ability, once learned, can be extracted and transferred between models as a compact task vector. We source two publicly available, identically initialized Qwen2.5 models, one fine-tuned with supervised fine-tuning (SFT) and the other with group relative policy optimization (GRPO) on the same dataset. From these, we extract a reasoning vector: $v_{\text{reason}} = \theta_{\text{GRPO}} - \theta_{\text{SFT}}$. We hypothesize that this vector captures the reasoning capability instilled by reinforcement learning while factoring out shared knowledge from the SFT process. When added to compatible instruction-tuned models through simple arithmetic, this vector consistently improves performance across diverse reasoning benchmarks: GSM8K (+4.9%), HumanEval (+4.3%), SciQ (+1.7%), and BigBenchHard (+12.3% for the 1.5B model). The performance improvements persist under adversarial conditions. Conversely, subtracting the vector causes significant performance degradation (-11.8% on GSM8K), demonstrating the vector's strong contribution to the model's reasoning abilities. This work shows how reasoning capabilities, typically developed through expensive training, can be extracted from existing open-source models and reused through simple tensor arithmetic, offering a practical way to enhance models by recycling prior computational investments.

• The paper shows that subtracting SFT model parameters from RL-tuned models yields a reasoning vector that enhances chain-of-thought capabilities.
• It uses task arithmetic with element-wise tensor operations to efficiently transfer reasoning skills between models with identical architectures.
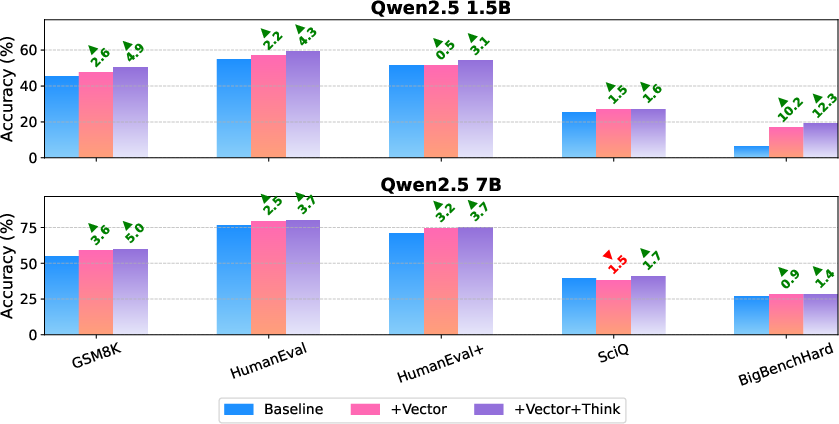
• Experimental results on benchmarks such as GSM8K and HumanEval confirm significant accuracy gains, underscoring the approach's robustness and scalability.

Reasoning Vectors: Modular Transfer of Chain-of-Thought Capabilities via Task Arithmetic

Introduction

The paper "Reasoning Vectors: Transferring Chain-of-Thought Capabilities via Task Arithmetic" (2509.01363) presents a method for extracting and transferring reasoning abilities in LLMs as explicit parameter-space vectors. The approach leverages the observation that reinforcement learning (RL) fine-tuning, such as Group Relative Policy Optimization (GRPO), imparts distinct reasoning capabilities to LLMs, which can be isolated by subtracting the parameters of a supervised fine-tuned (SFT) model from its RL-tuned counterpart. The resulting "reasoning vector" can then be added to other compatible models, conferring improved multi-step reasoning without additional training. This work situates itself at the intersection of task arithmetic, model merging, and modular capability transfer, providing a practical and computationally efficient alternative to repeated RL fine-tuning.

Methodology

Extraction and Application of Reasoning Vectors

The core procedure involves three models with identical architectures and initializations:

• $\theta_0$: Pretrained base model.
• $\theta_f$: SFT model, fine-tuned on a reasoning dataset (e.g., GSM8K) with cross-entropy loss.
• $\theta_r$: RL-tuned model, further optimized from $\theta_f$ using GRPO with a reasoning-focused reward.

The reasoning vector is defined as:

$v = \theta_r - \theta_f$

This vector is hypothesized to encode the parameter changes specifically attributable to RL-induced reasoning, with shared knowledge from SFT factored out.

To transfer reasoning, the vector is added to a compatible instruction-tuned target model $\theta_t$:

$\theta_{t,\text{enhanced}} = \theta_t + v$

Optionally, a scaling factor $\alpha$ and a binary mask $\mathbf{m}$ can be used for fine-grained control:

$$\theta_{t,\text{enhanced}} = \theta_t + \alpha \cdot (\mathbf{m} \odot v)$$

Empirically, $\alpha=1$ and $\mathbf{m} = \mathbf{1}$ (full vector, no masking) yield optimal results.

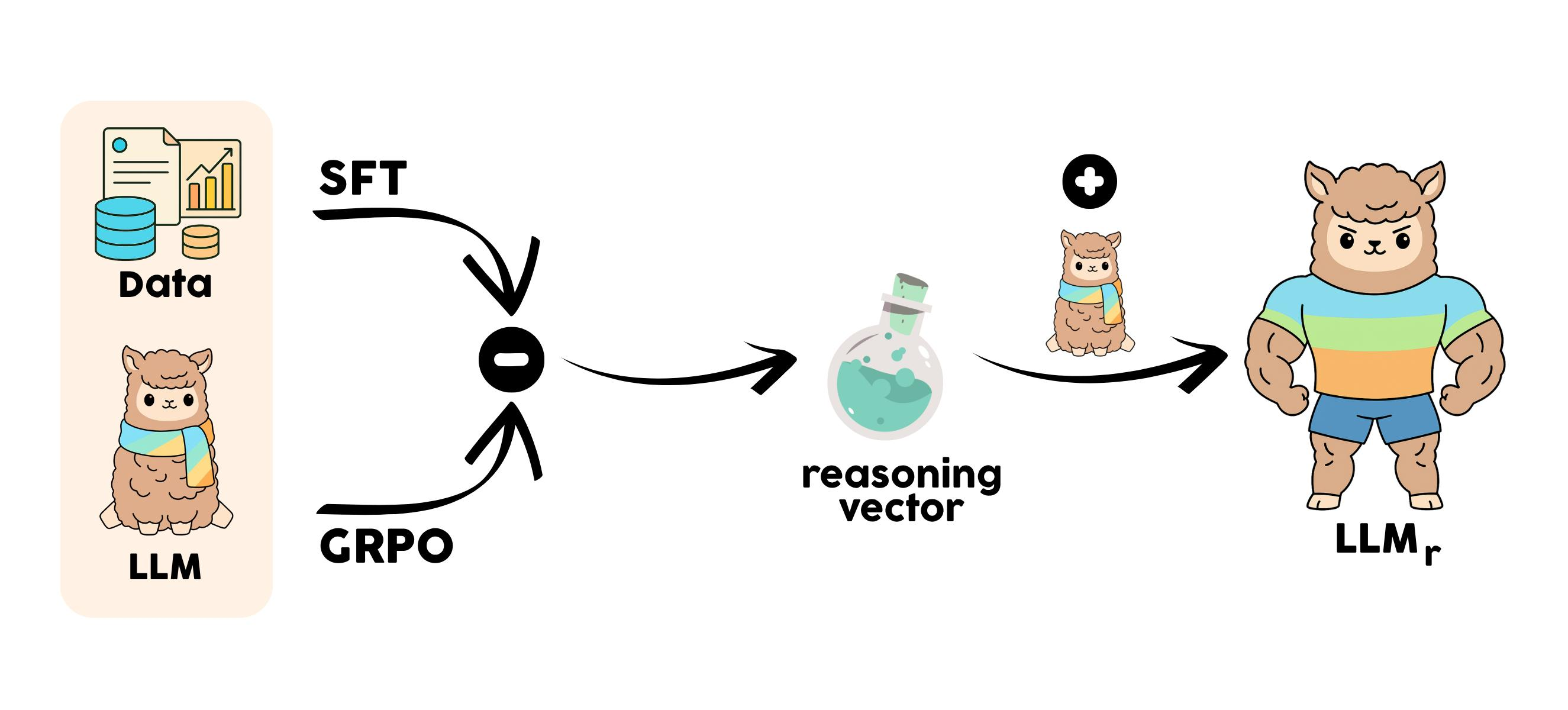
Figure 1: Merging the fine-tuning and reasoning vectors. Adding the reasoning vector $v$ to a base model transfers RL-induced reasoning capabilities.

Theoretical Justification

The method relies on Linear Mode Connectivity (LMC), which states that models fine-tuned from the same initialization typically reside in a connected low-loss region of parameter space. Thus, moving along the vector $v$ does not leave the low-loss basin, ensuring that the transfer does not destabilize the model.

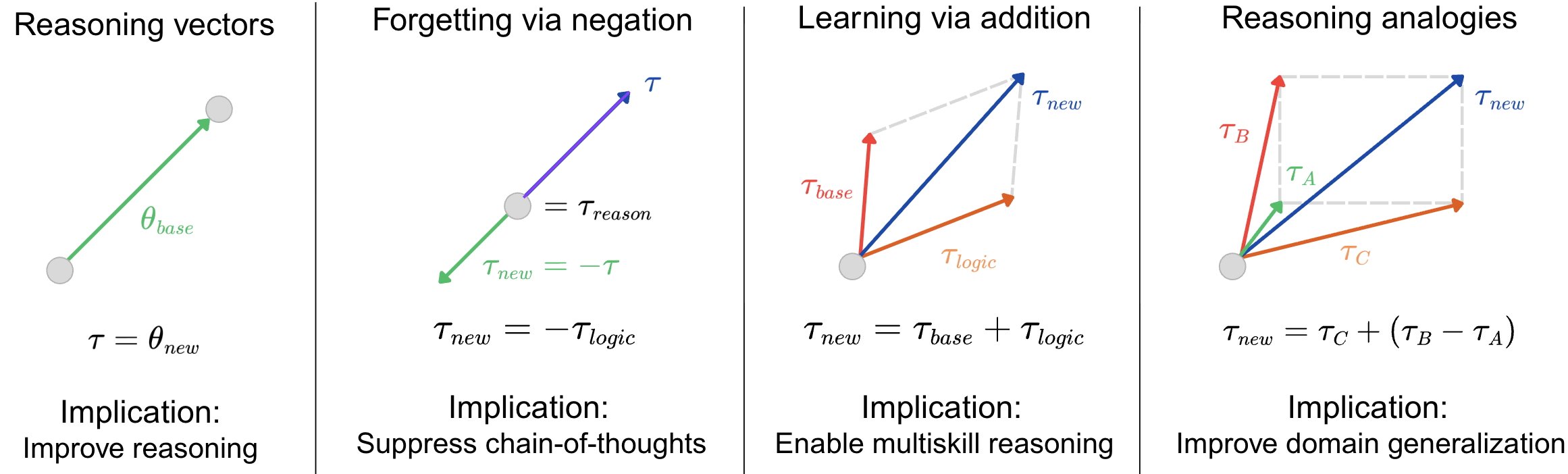
Figure 2: Reasoning vector operations in weight space: injection, negation, addition, and analogy-style composition.

Implementation

The extraction and transfer are implemented as two tensor operations, requiring only element-wise subtraction and addition. Compatibility is critical: models must share architecture, tokenizer, and initialization. The MergeKit library is used for efficient parameter manipulation.

Prompting with "Think step by step" further activates the transferred reasoning, indicating that the vector encodes latent capabilities that benefit from explicit activation cues.

Experimental Results

Benchmarks and Evaluation

The method is evaluated on Qwen2.5 models (1.5B and 7B parameters) across GSM8K (math), HumanEval/HumanEval+ (code), SciQ (science QA), and BigBenchHard (multi-hop reasoning). Four configurations are compared: baseline, RL-tuned donor, vector-enhanced, and vector-enhanced with reasoning prompt.

Figure 3: Evaluation prompt templates for HumanEval and GSM8K, isolating effects of parameter modification and explicit reasoning prompts.

Main Findings

• Consistent accuracy improvements are observed across all benchmarks and both model sizes.
  • Qwen2.5 1.5B: GSM8K +4.9%, HumanEval +4.3%, BigBenchHard +12.3%.
  • Qwen2.5 7B: GSM8K +5.0%, HumanEval +3.7%, BigBenchHard +1.4%.
• Prompting further amplifies gains, especially on complex tasks.
• Ablation by vector subtraction causes severe degradation (e.g., -11.8% on GSM8K), confirming the vector's functional role.
• Scaling analysis shows the vector is well-calibrated; $\alpha=1$ is optimal.
• Cross-domain transfer yields modest but nontrivial improvements, indicating partial generality of the reasoning vector.

  Figure 4: Accuracy improvements from reasoning vector transfer across five benchmarks for Qwen2.5 1.5B and 7B models.

Robustness

The vector-enhanced models maintain their advantage under adversarial perturbations, including increased problem complexity, injected noise, and sentence shuffling. Gains of 2–6% over baseline persist in all conditions, indicating that the vector encodes robust, non-brittle reasoning strategies.

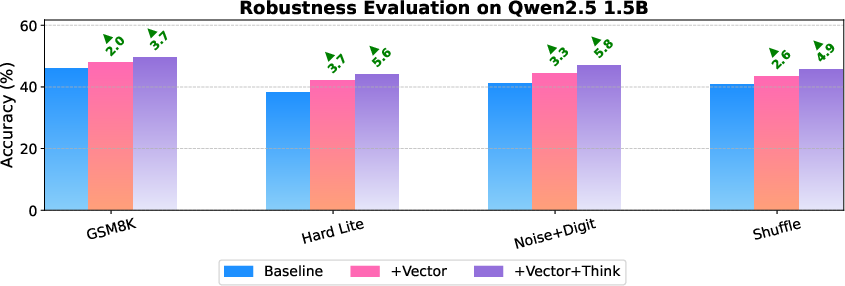
Figure 5: Robustness of Qwen2.5 1.5B under four perturbation conditions. The reasoning vector provides consistent gains.

Qualitative Analysis

Sample outputs demonstrate that vector removal leads to incoherent or misapplied reasoning steps, while vector addition restores correct multi-step solution paths and structured output formatting. This qualitative shift is consistent with the observed quantitative improvements.

Limitations

• Strict compatibility requirements: The method is only applicable between models with identical architectures, tokenizers, and initialization. Cross-family transfer (e.g., Llama to Qwen) is not supported.
• Dependence on donor availability: The approach presupposes the existence of both SFT and RL-tuned checkpoints for the same base model, externalizing the initial RL training cost.
• Partial generality: While some cross-domain transfer is observed, the reasoning vector is most effective when the target task is closely related to the RL training domain.

Implications and Future Directions

This work demonstrates that reasoning can be modularized as a vector in parameter space, enabling efficient transfer of cognitive capabilities without retraining. The approach democratizes access to advanced reasoning by leveraging open-source checkpoints and lightweight tensor operations. The findings suggest that other high-level skills (e.g., tool use, long-context reasoning) may also be extractable as vectors, opening avenues for compositional model editing and rapid capability bootstrapping.

Future research should address:

• Relaxing compatibility constraints via alignment or re-basing techniques.
• Automated discovery of transferable vectors for a broader range of skills.
• Compositionality and interference when combining multiple skill vectors.
• Theoretical analysis of the limits of vector modularity for complex cognitive functions.

Conclusion

The reasoning vector paradigm establishes that chain-of-thought capabilities, typically acquired through expensive RL fine-tuning, can be extracted and transferred as explicit parameter-space vectors. This enables modular, training-free enhancement of reasoning in LLMs, with strong empirical gains across mathematical, code, and logical reasoning tasks. The approach is robust, computationally efficient, and leverages the growing ecosystem of open-source model checkpoints. The modularity of reasoning in parameter space, as evidenced by symmetric ablation effects and cross-domain transfer, provides a foundation for future work on compositional and efficient model editing in large-scale AI systems.